Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-20T03:23:32.622Z Has data issue: false hasContentIssue false
  • English
  • Français

Periodic cohomology and subgroups with bounded Bredon cohomological dimension

Published online by Cambridge University Press:  01 March 2008

JANG HYUN JO  and
BRITA E. A. NUCINKIS
JANG HYUN JO
Affiliation:
Research Institute for Basic Science, Korea University, Seoul 136-701, Korea. e-mail: jhjo@sogang.ac.kr
BRITA E. A. NUCINKIS
Affiliation:
School of Mathematics, University of Southampton, SO17 1BJ. e-mail: B.E.A.Nucinkis@soton.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

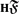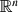Mislin and Talelli showed that a torsion-free group in with periodic cohomology after some steps has finite cohomological dimension. In this note we look at similar questions for groups with torsion by considering Bredon cohomology. In particular we show that every elementary amenable group acting freely and properly on some × Sm admits a finite dimensional model for G.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 144 , Issue 2 , March 2008 , pp. 329 - 336
Copyright
Copyright © Cambridge Philosophical Society 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bestvina, M. Questions in geometric group theory. http://www.math.utah.edu/~bestvina/eprints/questions-updated.pdf.Google Scholar
[2]Bieri, R. Homological dimension of discrete groups. Queen Mary College Mathematics Notes, 2nd ed. (1982).Google Scholar
[3]Flores, R. J. and Nucinkis, B. E. A.. On Bredon homology of elementary amenable groups. Proc. Amer. Math. Soc. 135 (2007), 5–11.CrossRefGoogle Scholar
[4]Hillman, J. A.Elementary amenable groups and 4-manifolds with Euler characteristic 0. J. Aust. Math. Soc. Ser. A 50 (1991), 160–170.CrossRefGoogle Scholar
[5]Jo, J. H.Multiple complexes and gaps in Farrell cohomology. J. Pure Appl. Algebra 194 (2004), 147–158.CrossRefGoogle Scholar
[6]Kropholler, P. H., Linnell, P. A. and Moody, J. A.. Applications of a new K-theoritic theorem to soluble group rings. Proc. Amer. Math. Soc. 104 (3), (1988), 675–684.Google Scholar
[7]Kropholler, P. H.On groups of type FP∞. J. Pure Appl. Algebra 90 (1993), 55–67.CrossRefGoogle Scholar
[8]Kropholler, P. H. and Mislin, G.. Groups acting on finite dimensional spaces with finite stablizers. Comment. Math. Helv. 73 (1998), 122–136.Google Scholar
[9]Lück, W. Transformation groups and algebraic K-theory. Lecture Notes in Math. 149 (Springer, 1989).Google Scholar
[10]Lück, W.The type of the classifying space for a family of subgroups. J. Pure Appl. Algebra 149 (2000), 177–203.CrossRefGoogle Scholar
[11]Martinez–Pérez, C.A spectral sequence in Bredon (co)homology. J. Pure Appl. Algebra 176 (2002), 161–173.CrossRefGoogle Scholar
[12]Mislin, G. Equivariant K-homology of classifying spaces for proper actions, in Proper group actions and the Baum–Connes conjecture. Adv. Courses Math. CRM Barcelona (Birkhauser, 2003), 1–78.CrossRefGoogle Scholar
[13]Mislin, G. and Talelli, O.. On groups which act freely and properly on finite dimensional homotopy spheres. in Computational and geometric aspects of modern algebra (Edinburgh, 1998). London Math. Soc. Lecture Note Ser. 275 (Cambridge University Press, 2000), 208–228.CrossRefGoogle Scholar
[14]Nucinkis, B. E. A.On dimensions in Bredon homology. Homology, Homotopy Appl. 6 (2004), no. 1, 33–47.Google Scholar
[15]Petrosyan, N. Periodicity and jumps in cohomology of R-torsion-free groups, preprint (2005).Google Scholar
[16]Stammbach, U.On the weak homological dimension of the group algebra of soluble groups. J. London Math. Soc. (2) 2 (1970), 567–570.CrossRefGoogle Scholar
[17]Talelli, O.On cohomological periodicity for infinite groups. Comment. Math. Helv. 55 (1980), 85–93.CrossRefGoogle Scholar
[18]Talelli, O.. Periodic cohomology and free and proper actions on ℝn × S m. London Math. Soc. Lecture Note Ser. 261, Groups St. Andrews 1997 in Bath, II. 261 (1997), 701–717.Google Scholar
[19]Talelli, O.Periodicity in group cohomology and complete resolutions. Bull. London Math. Soc. 37 (2005), 547–554.Google Scholar
[20]Talelli, O. On groups of type Φ, preprint (2005).Google Scholar
[21]Venkov, B. B.On homologies of groups of units in division algebras. Trudy Mat. Inst. Steklov. 80 (1965), 66–89. [English transtlation: Proc. Steklov Inst. Math. 80 (1965), 73–100.]Google Scholar
[22]Wehrfritz, B. A. F.On elementary amenable groups of finite Hirsch number. J. Austral. Math. Soc. Series A. 58 (1995), 219–221.Google Scholar