Article contents
Explicit generators for the relation module in the example of Gruenberg–Linnell
Published online by Cambridge University Press: 07 March 2016
Abstract
Gruenberg and Linnell showed that the standard relation module of a free product of n groups of the form Cr × 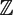 $\mathbb{Z}$ could be generated by just n + 1 generators, raising the possibility of a relation gap. We explicitly give such a set of generators.
$\mathbb{Z}$ could be generated by just n + 1 generators, raising the possibility of a relation gap. We explicitly give such a set of generators.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 161 , Issue 2 , September 2016 , pp. 199 - 202
- Copyright
- Copyright © Cambridge Philosophical Society 2016
References
REFERENCES
- 1
- Cited by


