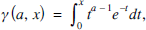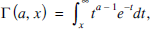Research Article
UK pension changes in 2015: some mathematical considerations
-
- Published online by Cambridge University Press:
- 14 June 2016, pp. 193-202
-
- Article
- Export citation
The mean-square value of the divisor function
-
- Published online by Cambridge University Press:
- 14 June 2016, pp. 203-212
-
- Article
- Export citation
Properties of Pythagorean quadrilaterals
-
- Published online by Cambridge University Press:
- 14 June 2016, pp. 213-224
-
- Article
- Export citation
A simple approach to solving cubic equations
-
- Published online by Cambridge University Press:
- 14 June 2016, pp. 225-232
-
- Article
- Export citation
An alternative recursive formula for the sums of powers of integers
-
- Published online by Cambridge University Press:
- 14 June 2016, pp. 233-238
-
- Article
- Export citation
Circles in areals
-
- Published online by Cambridge University Press:
- 14 June 2016, pp. 239-246
-
- Article
- Export citation
What is Bayesian statistics?
-
- Published online by Cambridge University Press:
- 14 June 2016, pp. 247-256
-
- Article
- Export citation
Using double integrals to solve single integrals
-
- Published online by Cambridge University Press:
- 14 June 2016, pp. 257-265
-
- Article
- Export citation
Euler, the clothoid and

-
- Published online by Cambridge University Press:
- 14 June 2016, pp. 266-273
-
- Article
- Export citation
An infinite product of nested radicals for log x from the Archimedean algorithm
-
- Published online by Cambridge University Press:
- 14 June 2016, pp. 274-278
-
- Article
- Export citation
A simple proof of Euler's continued fraction of e1/M
-
- Published online by Cambridge University Press:
- 14 June 2016, pp. 279-287
-
- Article
- Export citation
Cyclotomy and the heptadecagon
-
- Published online by Cambridge University Press:
- 14 June 2016, pp. 288-297
-
- Article
- Export citation
The incomplete gamma functions
-
- Published online by Cambridge University Press:
- 14 June 2016, pp. 298-306
-
- Article
- Export citation
Obituary
Sir Erik Christopher Zeeman FRS 1925–2016
-
- Published online by Cambridge University Press:
- 14 June 2016, pp. 307-313
-
- Article
-
- You have access
- Export citation
Notes
100.16 The Diophantine equation n(x + y + z) = xyz
-
- Published online by Cambridge University Press:
- 14 June 2016, p. 314
-
- Article
- Export citation
100.17 The vector triple product and planar vector algebra
-
- Published online by Cambridge University Press:
- 14 June 2016, pp. 314-317
-
- Article
- Export citation
100.18 Newton's semicircle and the probability integral
-
- Published online by Cambridge University Press:
- 14 June 2016, pp. 317-321
-
- Article
- Export citation
100.19 A quick evaluation of

-
- Published online by Cambridge University Press:
- 14 June 2016, pp. 321-323
-
- Article
- Export citation
100.20 Outside the box
-
- Published online by Cambridge University Press:
- 14 June 2016, pp. 323-329
-
- Article
- Export citation
100.21 Generalising the arbelos
-
- Published online by Cambridge University Press:
- 14 June 2016, pp. 329-335
-
- Article
- Export citation


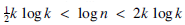 so that
so that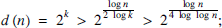
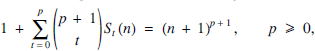
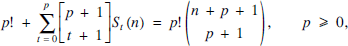
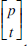 denote the (unsigned) Stirling numbers of the first kind, also known as the Stirling cycle numbers (see e.g. [6, Chapter 6]). Table 1 shows the first few rows of the Stirling number triangle. Although the recursive formula (2) is by no means new, our purpose in dealing with recurrence (2) in this note is two-fold. On one hand, we aim to provide a new algebraic proof of (2) by making use of two related identities involving the harmonic numbers.
denote the (unsigned) Stirling numbers of the first kind, also known as the Stirling cycle numbers (see e.g. [6, Chapter 6]). Table 1 shows the first few rows of the Stirling number triangle. Although the recursive formula (2) is by no means new, our purpose in dealing with recurrence (2) in this note is two-fold. On one hand, we aim to provide a new algebraic proof of (2) by making use of two related identities involving the harmonic numbers.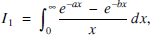
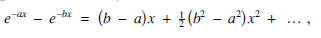
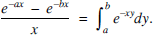

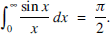
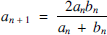
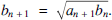
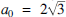 and
and 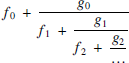
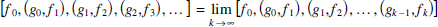
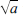 can be obtained by applying the intersecting chord theorem to a circle with diameter 1 +
can be obtained by applying the intersecting chord theorem to a circle with diameter 1 + 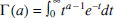 for
for