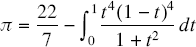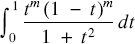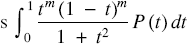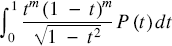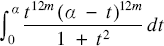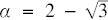Articles
Ratios in Heronian triangles
-
- Published online by Cambridge University Press:
- 18 June 2020, pp. 193-208
-
- Article
- Export citation
The three-square theorem of Gauss and Legendre
-
- Published online by Cambridge University Press:
- 18 June 2020, pp. 209-214
-
- Article
- Export citation
A family of discrete spirals
-
- Published online by Cambridge University Press:
- 18 June 2020, pp. 215-224
-
- Article
- Export citation
Tropical cycles
-
- Published online by Cambridge University Press:
- 18 June 2020, pp. 225-234
-
- Article
- Export citation
GPS navigation apps and the price of anarchy
-
- Published online by Cambridge University Press:
- 18 June 2020, pp. 235-240
-
- Article
- Export citation
Extensions of an identity of Euler
-
- Published online by Cambridge University Press:
- 18 June 2020, pp. 241-246
-
- Article
- Export citation
A more conclusive and more inclusive second derivative test
-
- Published online by Cambridge University Press:
- 18 June 2020, pp. 247-254
-
- Article
- Export citation
Two plane geometry problems approached through analytic geometry
-
- Published online by Cambridge University Press:
- 18 June 2020, pp. 255-261
-
- Article
- Export citation
A spiral pattern investigation: making mathematical connections
-
- Published online by Cambridge University Press:
- 18 June 2020, pp. 262-270
-
- Article
- Export citation
Parallel probabilities
-
- Published online by Cambridge University Press:
- 18 June 2020, pp. 271-280
-
- Article
- Export citation
Other
In the Pipeline for November 2020
-
- Published online by Cambridge University Press:
- 18 June 2020, p. 280
-
- Article
- Export citation
Articles
Markov Chain Monte Carlo on finite state spaces
-
- Published online by Cambridge University Press:
- 18 June 2020, pp. 281-287
-
- Article
- Export citation
Equations of some plane figures
-
- Published online by Cambridge University Press:
- 18 June 2020, pp. 288-295
-
- Article
- Export citation
New pancake series for π
-
- Published online by Cambridge University Press:
- 18 June 2020, pp. 296-303
-
- Article
- Export citation
Notes
104.12 From calendar coincidence to factorials to Ramanujan
-
- Published online by Cambridge University Press:
- 18 June 2020, pp. 304-306
-
- Article
- Export citation
104.13 An elementary geometric justification for the cofactor expansion of a 3 × 3 determinant
-
- Published online by Cambridge University Press:
- 18 June 2020, pp. 307-310
-
- Article
- Export citation
104.14 More on zero-over-zero limits of special type
-
- Published online by Cambridge University Press:
- 18 June 2020, pp. 310-313
-
- Article
- Export citation
104.15 Divergence of a modified harmonic series
-
- Published online by Cambridge University Press:
- 18 June 2020, pp. 313-315
-
- Article
- Export citation
104.16 Another function with discontinuous derivative
-
- Published online by Cambridge University Press:
- 18 June 2020, pp. 315-318
-
- Article
- Export citation
104.17 More proofs of the AM-GM inequality
-
- Published online by Cambridge University Press:
- 18 June 2020, pp. 318-326
-
- Article
- Export citation