No CrossRef data available.
Article contents
On the generalised birthday problem
Published online by Cambridge University Press: 01 August 2016
Extract
Probability theory abounds in counterintuitive results, perhaps the most celebrated being the answer to the birthday problem: what is the least value of n such that p (n, 2) > ½ where p (n, 2) denotes the probability that at least two out of n randomly chosen people have the same birthday? The question assumes birthdays are uniformly and independently distributed with leap years being ignored. The solution, n = 23, never fails to startle beginning students, and very often triggers an interest in the subject of probability. It is derived from the well-known observation that by the principle of complementation p (n, 2) is one minus the probability that no two have the same birthday, i.e.
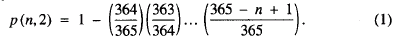
- Type
- Articles
- Information
- Copyright
- Copyright © The Mathematical Association 2004


