Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Sîntămărian, Alina
2010.
Regarding a generalisation of Ioachimescu's constant.
The Mathematical Gazette,
Vol. 94,
Issue. 530,
p.
270.
Sîntămărian, Alina
2011.
Sequences that converge quickly to a generalized Euler constant.
Mathematical and Computer Modelling,
Vol. 53,
Issue. 5-6,
p.
624.
Sîntămărian, Alina
2012.
Some new sequences that converge to a generalized Euler constant.
Applied Mathematics Letters,
Vol. 25,
Issue. 6,
p.
941.
Sîntămărian, Alina
2012.
New sequences that converge to a generalized Euler constant.
Analysis,
Vol. 32,
Issue. 2,
p.
111.
You, Xu
Chen, Di-Rong
and
Shi, Hong
2016.
Some new sequences that converge to the Ioachimescu constant.
Journal of Inequalities and Applications,
Vol. 2016,
Issue. 1,
You, Xu
2017.
On New Sequences Converging Towards the Ioachimescu’s Constant.
Results in Mathematics,
Vol. 71,
Issue. 3-4,
p.
1491.
You, Xu
2018.
Some sequences converging towards Ioachimescu’s constant related to Ramanujan’s formula.
The Ramanujan Journal,
Vol. 45,
Issue. 2,
p.
391.
Chen, Chao-Ping
2021.
Approximation formulas and inequalities for the Euler-Mascheroni constant.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 115,
Issue. 2,
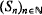 , defined by
, defined by 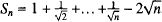 , for each
, for each 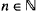 , is convergent and its limit lies between -2 and -1.
, is convergent and its limit lies between -2 and -1.

