Introduction
The InxGa1−xN alloy system and related heterostructures such as quantum wells (QWs) are attracting much attention because of their scientific and technological importance. This has been manifested by recent breakthroughs in the development of high-efficiency blue light emitting diodes and laser diodes using InxGa1−xN/GaN QW structures as active media materials. A large number of studies on the optical properties of InGaN epilayers and InGaN/GaN QW structures have been reported. In particular, recent pressure-dependent photoluminescence (PL) studies on bulk-like InxGa1−xN epitaxial layers have found that the pressure coefficients of the PL emission from InGaN epilayers do not substantially differ from that of GaN.Reference Shan, Song, Feng, Schurman and Stall 1 , Reference Shan, Ager, Walukiewicz, Haller, McCluskey, Johnson and Bour 2 In addition, the pressure coefficient of GaN grown epitaxially on sapphire does not differ from that of bulk GaN,Reference Camphausen and Connell 3 suggesting that the highly defective region near the GaN/sapphire interface plastically deforms under applied pressure. The pressure dependent measurements are consistent with theoretical predictions of the pressure dependence of the band gap.Reference Christensen and Gorczyca 4 Recent pressure-dependent studies of the optical properties of InxGa1−xN/GaN QWs have found that the pressure coefficients of luminescence emission depend on QW sample structure and the In concentration.Reference Perlin, Iota, Weinstein, Wisniewski, Suski, Eliseev and Osinski 5 , Reference Perlin, Kisielowski, Iota, Weinstein, Mattos, Kruger, Weber and Yang 6 One explanation of these results is that highly localized states, with small pressure coefficients, could be involved in the emission processes in the QWs.
Here we present a high-pressure study of optical transitions in an In0.15Ga0.85N/GaN multiple quantum well (MQWs) sample. Both photomodulated transmission (PT) and photoluminescence (PL) measurements were performed. A comparison between the pressure dependence of the absorption process probed by PT and that of the emission process measured by PL provides direct insights into the nature of the electronic states involved.
Experiment
The In0.15Ga0.85N/GaN MQW sample used in this work is a laser diode structure prepared by metalorganic chemical vapor deposition. It consists of a 10-period In0.15Ga0.85N/GaN superlattice grown on a 4-μm thick GaN layer deposited on a sapphire substrate, and it is capped by a 0.2-μm GaN:Mg p-type layer. The thicknesses of the well and the barrier are 18 and 62 Å, respectively. These values were derived from X-ray diffraction (XRD) measurements of the superlattice period (80 Å) and the ratio of the well/barrier growth times (35/120). The averaged In concentration was determined by Rutherford backscattering spectrometry. The MQW structure is pseudomorphically strained to the underlaying GaN layers.Reference McCluskey, Van de Walle, Master, Romano and Johnson 7
Photomodulation measurements were performed in a transmission geometry using a 150W xenon lamp as probing light source and a chopped HeCd laser beam (3250 Å) as modulating light. PL signals resulted from excitation by the laser and were dispersed by a 1-M double-grating monochromator. Application of hydrostatic pressure was accomplished by mounting small sample chips with sizes of ∼200×200 µm2 into gasketed diamond anvil cells. A small ruby chip was also placed in the DAC for pressure calibration. All the spectra reported in this work were recorded at room temperature (295 K).
Results and Discussion
Fig.1 shows PT spectra taken from the In0.15Ga0.85N/GaN MQW sample and two thick epilayer samples (In0.15Ga0.85N and In0.11Ga0.89N) at ambient pressure. The derivative-like spectral signatures denoted as E0 in the spectra are associated with the optical transitions across the band gap of the respective samples. Note that the quantum confinement effects on the electron and hole states in the MQW have shifted the band gap of In0.15Ga0.85N to an energy approximately equal to that of bulk In0.11Ga0.89N. The second derivative-like spectral feature (denoted as E1) in the PT spectrum of the MQW is due to transitions from ionized Mg acceptor states to the conduction band edge in the p-type GaN cladding layer. As commonly observed in InGaN alloys and related heterostructure samples, the MQW sample exhibits fairly broad PT and PL spectral lineshapes. A Stokes shift of the PL peak energy (2.99 eV) relative to the transition energy (E0) was observed.

Fig. 1. PT spectra of an In0.15Ga0.85N/GaN MQW sample and two (In0.15Ga0.85N and In0.15Ga0.85N) epilayer samples at ambient pressure
The pressure induced energy shifts for the E0 transition and PL peak if the MQW sample, along with the PL emission from the thick In0.11Ga0.89N epilayer, are plotted in Fig.2. The inset of the figure shows a comparison of the PL spectra taken from these two samples. The solid lines in the figure are least-squares fits to the experimental data using the linearfit function
where the energy E is in eV and the pressure P is in kbar. The pressure coefficients for the E0 transition and the PL emission in MQWs were determined to be 3.0×10−3 eV/kbar and 2.8×10−3 eV/kbar, respectively. A best fit to the PL data of the In0.11Ga0.89N sample yields a pressure coefficient of 4.0×10−3 eV/kbar. The pressure dependence of the interband E0 transition and the PL emission in the MQW sample is much weaker than that of thick, bulk-like In0.11Ga0.89N epitaxial layer. Although weaker pressure dependences of PL emissions in InGaN/GaN quantum wells were previously reported,Reference Shan, Song, Feng, Schurman and Stall 1 , Reference Shan, Ager, Walukiewicz, Haller, McCluskey, Johnson and Bour 2 this is the first time that a significantly smaller pressure dependence of an interband absorption in InGaN/GaN MQWs has been observed. The fact that the pressure coefficient obtained by PT measurements is very similar to that derived from PL measurements infers that the possibility of the PL transition involving deep localized states can be ruled out safely and it further demonstrates that the PL process originates from the effective-mass band-edge states in the MQW sample.

Fig.2. Shift of the PT transition and PL emission energies for the MQW sample and the In0.11Ga0.89N epilayer sample as a function of applied pressure. The solid lines are the linear fits to the data. The inset shows the PL spectra of the samples at ambient pressure.
Application of hydrostatic pressure to strained QWs consisting of barrier and well materials with very different bulk moduli will lead to uniaxial strains that make the barriers and the wells experience different effective hydrostatic and axial pressure components.Reference Gil, Dunstan, Calatayud, Mathieu and Faurie 8 , Reference Tuchman and Herman 9 Since the MQW structure used in this work was grown on a thick GaN layer, and the GaN barriers are much thicker than the In0.15Ga0.85N wells, the deformation of the well layers is dominated by the compression of the stiffer GaN under hydrostatic pressure. The bulk modulus of InN (∼125 GPa)Reference Ueno, Yoshida, Onodera, Shimomura and Takemura 10 is approximately half of that of GaN (∼210-237 GPa).Reference Ueno, Yoshida, Onodera, Shimomura and Takemura 10 - Reference Polian, Grimsditch and Grzegory 12 A linear interpolation gives a bulk modulus of In0.15Ga0.85N about 7% smaller than that of GaN. Under hydrostatic pressure conditions, a tensile strain will be induced in the compressively strained In0.15Ga0.85N well layers in the MQW structure to compensate the applied hydrostatic pressure because In0.15Ga0.85N has a larger compressibility. As a result, the In0.15Ga0.85N layers effectively experience a smaller hydrostatic pressure and an additional (0001) uniaxial stress. The relative volume change with applied pressure can be estimated using the Murnaghan equation of state:Reference Murnaghan 13
Here B0 is the bulk modulus and B0′ is its pressure derivative (=dB/dP). For a crystal with wurtzite structure, the relative volume change can be related to the variation of lattice parameters a and c as:
The relative changes of the lattice parameters can further be related through the elastic stiffness coefficients as:
Under the conditions that the In0.15Ga0.85N well layers remain pseudomorphically strained to GaN at high pressures, the variation of the a-lattice parameter of the well layers has to match the change of the a-lattice constant of GaN under pressure. Using the first-order (linear) approximation, the relative changes of the c-lattice constant as a function of applied hydrostatic pressure for a pseudomorphically strained to GaN and strain-free (free standing) In0.15Ga0.85N layer can be expressed as:
and
respectively. The calculated results are given in Fig.3. The numerical values of C 13=108 GPa and C 33=399 GPa for GaN and C 13=94 GPa and C 33=200 GPa for InN were used, and no fitting parameters were invoked in the calculations. As is shown in the figure, the overall effect of mechanical strain is to make a strained In0.15Ga0.85N layer sandwiched by stiffer GaN layers be compressed less than a free-standing layer at a given externally applied hydrostatic pressure. The effective pressure experienced by the well layers is only about 74% of the applied pressure. A pressure coefficient of 3.7−4.0×10−3 eV/kbar can be derived from this purely mechanical correction. Fig.4 shows this mechanical correction to the experimental data. Therefore, we attribute the difference in the compressibility of In0.15Ga0.85N from that of GaN to be the major factor responsible for the significantly weaker pressure dependence of the confined transition in our MQW sample.

Fig.3. Relative change of the c-lattice constant of an In0.15Ga0.85N layer pseudomorphically strained to GaN (solid line) and a strain-free In0.15Ga0.85N layer (dashed line) as a function of pressure.

Fig.4. Comparison of the PT and PL transition energy shifts in the MQW sample as a function of pressure after the mechanical correction to the
We also found the PL intensities from the MQWs and the In0.11Ga0.89N sample experienced a sudden drop as the applied pressure rises above 100 kbar, whereas their luminescence intensities did not change much at pressures below 100 kbar, as shown in Fig.5. While the PL intensity of the epilayer sample was found to decrease by a factor of four, the PL signal from the MQW in fact was quenched completely at pressures beyond 100 kbar. This observation provides direct evidence that the PL emission from the MQW sample is dominated by contributions from the carriers photo-generated in the GaN cladding, barrier and underlying layers. After being generated in the GaN layers, electrons and holes diffuse into the well regions, and thermalize down to the lowest confined states, respectively, where they radiatively recombine to produce PL emissions. At pressures beyond 100 kbar, the band-gap energy of GaN becomes larger than the photon energy of the excitation laser line (3.81 eV), so that very few carriers could be generated in the GaN layers. At that point, the PL emission from the MQW collapsed, indicating that the carriers created directly in the very-thin well layers do not contribute noticeably to the PL signal at room temperature. The residual PL emission in the epilayer sample above 100 kbar is primarily due to its large thickness.
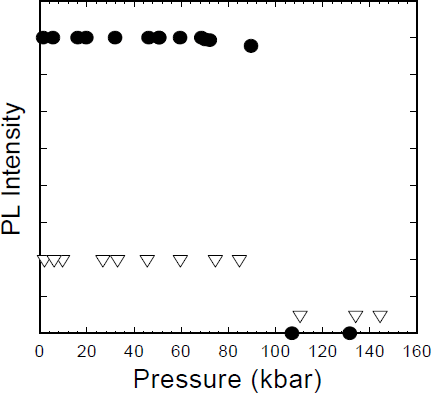
Fig.5. Change of PL intensities with pressure for the MQW sample (solid circles) and the In0.11Ga0.89N sample (open triangles). experimental data.
Conclusions
We found that both PT and PL spectral features corresponding to the transition associated with the confined states in an In0.15Ga0.85N/GaN MQWs exhibit a significantly smaller pressure dependence as compared to bulk-like thick InGaN epitaxial-layer samples. The very similar pressure coefficients obtained by monitoring two different transition processes, i.e., absorption (PT) and recombination (PL), rule out the possibility of PL resulting from localized states deep in the band gap. The difference in the compressibilities of In0.15Ga0.85N and GaN, which induces a tensile strain in the In0.15Ga0.85N well layers, partially compensating the externally applied hydrostatic pressure, was found to be primarily responsible for the smaller pressure dependence obsserved for the confined transition in the MQW sample. An abrupt decrease of PL intensity in the MQW and In0.11Ga0.89N samples was also observed at pressures above 100 kbar. The loss of the supply of photo-carriers from GaN layers above 100 kbar is found to be responsible for the sudden drop of the PL intensity in the epilayer sample and the quenching of the PL signal in the MQW sample at room temperature because the band gap of GaN exceeds the photon energy of the excitation light source.
Acknowledgments
The authors gratefully acknowledge the technical support by Professor P.Y. Yu and helpful discussions with P. Perlin. This work at LBNL was supported by the Director, Office of Energy Research, Office of Basic Research, Materials Sciences Division of the U.S. Department of Energy under Contract No.DE-AC03-76SF00098.






