Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T00:18:33.909Z Has data issue: false hasContentIssue false
  • English
  • Français

Visualizing elements of order 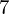$7$ in the Tate–Shafarevich group of an elliptic curve

Part of: Arithmetic algebraic geometry

Published online by Cambridge University Press:  26 August 2016

Tom Fisher
Tom Fisher*
Affiliation:
University of Cambridge, DPMMS, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WB, United Kingdom email T.A.Fisher@dpmms.cam.ac.uk

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the elliptic curves in Cremona’s tables that are predicted by the Birch–Swinnerton-Dyer conjecture to have elements of order 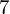$7$ in their Tate–Shafarevich group. We show that in many cases these elements are visible in an abelian surface or abelian 3-fold.

MSC classification

Primary: 11G05: Elliptic curves over global fields 11G30: Curves of arbitrary genus or genus $ne 1$ over global fields
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 19 , Special Issue A: Algorithmic Number Theory Symposium XII , 2016 , pp. 100 - 114
Copyright
© The Author 2016 

References

Adler, A. and Ramanan, S., Moduli of abelian varieties , Lecture Notes in Mathematics 1644 (Springer, Berlin, 1996).Google Scholar
Agashé, A. and Stein, W. A., ‘Visibility of Shafarevich–Tate groups of abelian varieties’, J. Number Theory 97 (2002) no. 1, 171–185.CrossRefGoogle Scholar
Agashé, A. and Stein, W. A., ‘Visible evidence for the Birch and Swinnerton-Dyer conjecture for modular abelian varieties of analytic rank zero, with an appendix by J. E. Cremona and B. Mazur’, Math. Comp. 74 (2005) no. 249, 455–484.CrossRefGoogle Scholar
An, S. Y., Kim, S. Y., Marshall, D. C., Marshall, S. H., McCallum, W. G. and Perlis, A. R., ‘Jacobians of genus one curves’, J. Number Theory 90 (2001) no. 2, 304–315.Google Scholar
Bending, P. R., ‘Curves of genus $2$ with $\sqrt{2}$ multiplication’, Preprint, 1999, arXiv:9911273.Google Scholar
Bosch, S., Lütkebohmert, W. and Raynaud, M., Néron models , Ergebnisse der Mathematik und ihrer Grenzgebiete (3) 21 (Springer, Berlin, 1990).Google Scholar
Bosma, W., Cannon, J. and Playoust, C., ‘The Magma algebra system I: The user language’, J. Symbolic Comput. 24 (1997) 235–265, see also http://magma.maths.usyd.edu.au/magma/.Google Scholar
Cassels, J. W. S. and Flynn, E. V., Prolegomena to a middlebrow arithmetic of curves of genus 2 , LMS Lecture Note Series 230 (Cambridge University Press, Cambridge, 1996).Google Scholar
Cremona, J. E., Algorithms for modular elliptic curves (Cambridge University Press, Cambridge, 1997) See also http://www.warwick.ac.uk/∼masgaj/ftp/data/.Google Scholar
Cremona, J. E. and Mazur, B., ‘Visualizing elements in the Shafarevich–Tate group’, Exp. Math. 9 (2000) no. 1, 13–28.CrossRefGoogle Scholar
Fisher, T. A., ‘Finding rational points on elliptic curves using 6-descent and 12-descent’, J. Algebra 320 (2008) no. 2, 853–884.Google Scholar
Fisher, T. A., ‘On families of 7 and 11-congruent elliptic curves’, LMS J. Comput. Math. 17 (2014) no. 1, 536–564.Google Scholar
Fisher, T. A., ‘Invisibility of Tate–Shafarevich groups in abelian surfaces’, Int. Math. Res. Not. IMRN 2014 no. 15, 4085–4099.Google Scholar
Flynn, E. V., Leprévost, F., Schaefer, E. F., Stein, W. A., Stoll, M. and Wetherell, J. L., ‘Empirical evidence for the Birch and Swinnerton-Dyer conjectures for modular Jacobians of genus 2 curves’, Math. Comp. 70 (2001) no. 236, 1675–1697.Google Scholar
González-Jiménez, E., González, J. and Guàrdia, J., ‘Computations on modular Jacobian surfaces’, Algorithmic number theory (Sydney, 2002) , Lecture Notes in Computational Science 2369 (Springer, Berlin, 2002) 189–197.Google Scholar
Grigorov, G., Jorza, A., Patrikis, S., Stein, W. A. and Tarnita, C., ‘Computational verification of the Birch and Swinnerton-Dyer conjecture for individual elliptic curves’, Math. Comp. 78 (2009) no. 268, 2397–2425.Google Scholar
Halberstadt, E. and Kraus, A., ‘Sur la courbe modulaire X E (7)’, Exp. Math. 12 (2003) no. 1, 27–40.Google Scholar
Kraus, A. and Oesterlé, J., ‘Sur une question de B. Mazur’, Math. Ann. 293 (1992) no. 2, 259–275.Google Scholar
Mazur, B., ‘Visualizing elements of order three in the Shafarevich–Tate group’, Asian J. Math. 3 (1999) no. 1, 221–232.Google Scholar
Merriman, J. R. and Smart, N. P., ‘Curves of genus 2 with good reduction away from 2 with a rational Weierstrass point’, Math. Proc. Cambridge Philos. Soc. 114 (1993) no. 2, 203–214.CrossRefGoogle Scholar
PARI/GP, Version 2.5.5, Bordeaux, 2013, http://pari.math.u-bordeaux.fr/.Google Scholar
Poonen, B., Schaefer, E. F. and Stoll, M., ‘Twists of X (7) and primitive solutions to x 2 + y 3 = z 7 ’, Duke Math. J. 137 (2007) no. 1, 103–158.Google Scholar
Schaefer, E. F., ‘Class groups and Selmer groups’, J. Number Theory 56 (1996) no. 1, 79–114.Google Scholar
Serre, J.-P., ‘Propriétés galoisiennes des points d’ordre fini des courbes elliptiques’, Invent. Math. 15 (1972) no. 4, 259–331.CrossRefGoogle Scholar
Shimura, G., ‘On the factors of the Jacobian variety of a modular function field’, J. Math. Soc. Japan 25 (1973) 523–544.Google Scholar
Siksek, S., ‘Infinite descent on elliptic curves’, Rocky Mountain J. Math. 25 (1995) no. 4, 1501–1538.Google Scholar
Silverman, J. H., ‘The Néron fiber of abelian varieties with potential good reduction’, Math. Ann. 264 (1983) no. 1, 1–3.Google Scholar
Silverman, J. H., The arithmetic of elliptic curves , Graduate Text in Mathematics 106 (Springer, New York, 1986).CrossRefGoogle Scholar
Stein, W. A. et al. , ‘Sage Mathematics Software (Version 6.2)’, The Sage Development Team, 2014, http://www.sagemath.org.Google Scholar
Stoll, M., ‘Two simple 2-dimensional abelian varieties defined over ℚ with Mordell–Weil group of rank at least 19’, C. R. Math. Acad. Sci. Paris 321 (1995) no. I, 1341–1345.Google Scholar
Vélu, J., ‘Isogénies entre courbes elliptiques’, C. R. Math. Acad. Sci. Paris Sér. A-B 273 (1971) A238–A241.Google Scholar
van Wamelen, P. B., ‘Computing with the analytic Jacobian of a genus 2 curve’, Discovering mathematics with Magma , Algorithms and Computation in Mathematics 19 (eds Bosma, W. and Cannon, J.; Springer, Berlin, 2006) 117–135.Google Scholar
Wang, X. D., ‘2-dimensional simple factors of J 0(N)’, Manuscripta Math. 87 (1995) no. 2, 179–197.Google Scholar