No CrossRef data available.
Article contents
Václav Šimerka: quadratic forms and factorization
Published online by Cambridge University Press: 01 May 2013
Abstract
In this article we show that the Czech mathematician Václav Šimerka discovered the factorization of 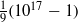 $\frac{1}{9} (1{0}^{17} - 1)$ using a method based on the class group of binary quadratic forms more than 120 years before Shanks and Schnorr developed similar algorithms. Šimerka also gave the first examples of what later became known as Carmichael numbers.
$\frac{1}{9} (1{0}^{17} - 1)$ using a method based on the class group of binary quadratic forms more than 120 years before Shanks and Schnorr developed similar algorithms. Šimerka also gave the first examples of what later became known as Carmichael numbers.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2013


