Article contents
Tuple lattice sieving
Published online by Cambridge University Press: 26 August 2016
Abstract
Lattice sieving is asymptotically the fastest approach for solving the shortest vector problem (SVP) on Euclidean lattices. All known sieving algorithms for solving the SVP require space which (heuristically) grows as 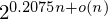 $2^{0.2075n+o(n)}$, where
$2^{0.2075n+o(n)}$, where 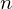 $n$ is the lattice dimension. In high dimensions, the memory requirement becomes a limiting factor for running these algorithms, making them uncompetitive with enumeration algorithms, despite their superior asymptotic time complexity.
$n$ is the lattice dimension. In high dimensions, the memory requirement becomes a limiting factor for running these algorithms, making them uncompetitive with enumeration algorithms, despite their superior asymptotic time complexity.
We generalize sieving algorithms to solve SVP with less memory. We consider reductions of tuples of vectors rather than pairs of vectors as existing sieve algorithms do. For triples, we estimate that the space requirement scales as 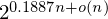 $2^{0.1887n+o(n)}$. The naive algorithm for this triple sieve runs in time
$2^{0.1887n+o(n)}$. The naive algorithm for this triple sieve runs in time  $2^{0.5661n+o(n)}$. With appropriate filtering of pairs, we reduce the time complexity to
$2^{0.5661n+o(n)}$. With appropriate filtering of pairs, we reduce the time complexity to 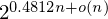 $2^{0.4812n+o(n)}$ while keeping the same space complexity. We further analyze the effects of using larger tuples for reduction, and conjecture how this provides a continuous trade-off between the memory-intensive sieving and the asymptotically slower enumeration.
$2^{0.4812n+o(n)}$ while keeping the same space complexity. We further analyze the effects of using larger tuples for reduction, and conjecture how this provides a continuous trade-off between the memory-intensive sieving and the asymptotically slower enumeration.
MSC classification
- Type
- Research Article
- Information
- LMS Journal of Computation and Mathematics , Volume 19 , Special Issue A: Algorithmic Number Theory Symposium XII , 2016 , pp. 146 - 162
- Copyright
- © The Author(s) 2016
References
- 30
- Cited by


