Article contents
On error distributions in ring-based LWE
Published online by Cambridge University Press: 26 August 2016
Abstract
Since its introduction in 2010 by Lyubashevsky, Peikert and Regev, the ring learning with errors problem (ring-LWE) has become a popular building block for cryptographic primitives, due to its great versatility and its hardness proof consisting of a (quantum) reduction from ideal lattice problems. But, for a given modulus 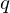 $q$ and degree
$q$ and degree 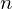 $n$ number field
$n$ number field 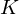 $K$, generating ring-LWE samples can be perceived as cumbersome, because the secret keys have to be taken from the reduction mod
$K$, generating ring-LWE samples can be perceived as cumbersome, because the secret keys have to be taken from the reduction mod 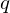 $q$ of a certain fractional ideal
$q$ of a certain fractional ideal 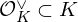 ${\mathcal{O}}_{K}^{\vee }\subset K$ called the codifferent or ‘dual’, rather than from the ring of integers
${\mathcal{O}}_{K}^{\vee }\subset K$ called the codifferent or ‘dual’, rather than from the ring of integers 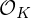 ${\mathcal{O}}_{K}$ itself. This has led to various non-dual variants of ring-LWE, in which one compensates for the non-duality by scaling up the errors. We give a comparison of these versions, and revisit some unfortunate choices that have been made in the recent literature, one of which is scaling up by
${\mathcal{O}}_{K}$ itself. This has led to various non-dual variants of ring-LWE, in which one compensates for the non-duality by scaling up the errors. We give a comparison of these versions, and revisit some unfortunate choices that have been made in the recent literature, one of which is scaling up by 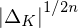 ${|\unicode[STIX]{x1D6E5}_{K}|}^{1/2n}$ with
${|\unicode[STIX]{x1D6E5}_{K}|}^{1/2n}$ with 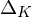 $\unicode[STIX]{x1D6E5}_{K}$ the discriminant of
$\unicode[STIX]{x1D6E5}_{K}$ the discriminant of 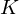 $K$. As a main result, we provide, for any
$K$. As a main result, we provide, for any 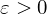 $\unicode[STIX]{x1D700}>0$, a family of number fields
$\unicode[STIX]{x1D700}>0$, a family of number fields 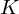 $K$ for which this variant of ring-LWE can be broken easily as soon as the errors are scaled up by
$K$ for which this variant of ring-LWE can be broken easily as soon as the errors are scaled up by 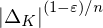 ${|\unicode[STIX]{x1D6E5}_{K}|}^{(1-\unicode[STIX]{x1D700})/n}$.
${|\unicode[STIX]{x1D6E5}_{K}|}^{(1-\unicode[STIX]{x1D700})/n}$.
MSC classification
- Type
- Research Article
- Information
- LMS Journal of Computation and Mathematics , Volume 19 , Special Issue A: Algorithmic Number Theory Symposium XII , 2016 , pp. 130 - 145
- Copyright
- © The Author(s) 2016
References
- 10
- Cited by


