Hostname: page-component-8448b6f56d-mp689 Total loading time: 0 Render date: 2024-04-19T07:27:39.768Z Has data issue: false hasContentIssue false
  • English
  • Français

Minimal models for 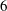$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}6$-coverings of elliptic curves

Part of: Curves Arithmetic algebraic geometry

Published online by Cambridge University Press:  01 August 2014

Tom Fisher
Tom Fisher*
Affiliation:
University of Cambridge, DPMMS, Centre for Mathematical Sciences, Wilberforce Road, Cambridge, CB3 0WB, United Kingdom email T.A.Fisher@dpmms.cam.ac.uk

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we give a new formula for adding 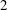$2$-coverings and 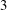$3$-coverings of elliptic curves that avoids the need for any field extensions. We show that the 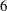$6$-coverings obtained can be represented by pairs of cubic forms. We then prove a theorem on the existence of such models with integer coefficients and the same discriminant as a minimal model for the Jacobian elliptic curve. This work has applications to finding rational points of large height on elliptic curves.

MSC classification

Secondary: 11G05: Elliptic curves over global fields 14H52: Elliptic curves
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 17 , Special Issue A: Algorithmic Number Theory Symposium XI , 2014 , pp. 112 - 127
Copyright
© The Author 2014 

References

An, S. Y., Kim, S. Y., Marshall, D. C., Marshall, S. H., McCallum, W. G. and Perlis, A. R., ‘Jacobians of genus one curves’, J. Number Theory 90 (2001) no. 2, 304–315.CrossRefGoogle Scholar
Bhargava, M. and Shankar, A., ‘Binary quartic forms having bounded invariants, and the boundedness of the average rank of elliptic curves’, Preprint, 2013, arXiv:1006.1002v3 [math.NT].Google Scholar
Bhargava, M. and Shankar, A., ‘Ternary cubic forms having bounded invariants, and the existence of a positive proportion of elliptic curves having rank 0’, Preprint, 2013, arXiv:1007.0052v2 [math.NT].Google Scholar
Bhargava, M. and Shankar, A., ‘The average number of elements in the 4-Selmer groups of elliptic curves is 7’, Preprint, 2013, arXiv:1312.7333 [math.NT].Google Scholar
Bhargava, M. and Shankar, A., ‘The average size of the 5-Selmer group of elliptic curves is 6, and the average rank is less than 1’, Preprint, 2013, arXiv:1312.7859 [math.NT].Google Scholar
Bhargava, M. and Ho, W., ‘Coregular spaces and genus one curves’, Preprint, 2013, arXiv:1306.4424 [math.AG].Google Scholar
Birkenhake, C. and Lange, H., Complex abelian varieties, 2nd edn,Grundlehren der Mathematischen Wissenschaften 302 (Springer, Berlin, 2004).Google Scholar
Bosma, W., Cannon, J. and Playoust, C., ‘The Magma algebra system I: the user language’, J. Symbolic Comput. 24 (1997) 235–265; see also the Magma home page at http://magma.maths.usyd.edu.au/magma/ .CrossRefGoogle Scholar
von Bothmer, H.-C. Graf and Hulek, K., ‘Geometric syzygies of elliptic normal curves and their secant varieties’, Manuscripta Math. 113 (2004) no. 1, 35–68.CrossRefGoogle Scholar
Cassels, J. W. S., ‘Arithmetic on curves of genus 1, IV. Proof of the Hauptvermutung’, J. reine angew. Math. 211 (1962) 95–112.Google Scholar
Clark, P. L., ‘The period-index problem in WC-groups, I. Elliptic curves’, J. Number Theory 114 (2005) no. 1, 193–208.CrossRefGoogle Scholar
Cremona, J. E., Fisher, T. A., O’Neil, C., Simon, D. and Stoll, M., ‘Explicit n-descent on elliptic curves, I. Algebra’, J. reine angew. Math. 615 (2008) 121–155.Google Scholar
Cremona, J. E., Fisher, T. A. and Stoll, M., ‘Minimisation and reduction of 2-, 3- and 4-coverings of elliptic curves’, Algebra Number Theory 4 (2010) no. 6, 763–820.CrossRefGoogle Scholar
Fisher, T. A., ‘Finding rational points on elliptic curves using 6-descent and 12-descent’, J. Algebra 320 (2008) no. 2, 853–884.CrossRefGoogle Scholar
Fisher, T. A., ‘The invariants of a genus one curve’, Proc. Lond. Math. Soc. (3) 97 (2008) 753–782.CrossRefGoogle Scholar
Fisher, T. A., ‘Pfaffian presentations of elliptic normal curves’, Trans. Amer. Math. Soc. 362 (2010) no. 5, 2525–2540.CrossRefGoogle Scholar
Fisher, T. A., ‘Minimisation and reduction of 5-coverings of elliptic curves’, Algebra Number Theory 7 (2013) no. 5, 1179–1205.CrossRefGoogle Scholar
Gross, B. H., ‘On Bhargava’s representation and Vinberg’s invariant theory’, Frontiers of mathematical sciences (eds Gu, B. and Yau, S.-T.; International Press, Somerville, MA, 2011) 317–321.Google Scholar
Gross, M. and Popescu, S., ‘Equations of (1, d)-polarized abelian surfaces’, Math. Ann. 310 (1998) no. 2, 333–377.CrossRefGoogle Scholar
Harris, J., Algebraic geometry, a first course, Graduate Texts in Mathematics 133 (Springer, New York, 1992).Google Scholar
Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics 52 (Springer, New York, 1977).CrossRefGoogle Scholar
Hulek, K., ‘Projective geometry of elliptic curves’, Astérisque 137 (1986).Google Scholar
Mumford, D., ‘Varieties defined by quadratic equations’, Questions on Algebraic Varieties (C.I.M.E., III Ciclo, Varenna, 1969) (Edizioni Cremonese, Rome, 1970) 29–100.Google Scholar
O’Neil, C., ‘The period-index obstruction for elliptic curves’, J. Number Theory 95 (2002) no. 2, 329–339.CrossRefGoogle Scholar
Room, T. G., The geometry of determinantal loci (Cambridge University Press, Cambridge, 1938).Google Scholar
Salmon, G., A treatise on the higher plane curves, 3rd edn (Hodges, Foster and Figgis, Dublin, 1879).Google Scholar
Stein, W. A. and Watkins, M., ‘A database of elliptic curves—first report’, Algorithmic number theory (Sydney 2002), Lecture Notes in Computer Science 2369 (Springer, Berlin, 2002) 267–275.CrossRefGoogle Scholar
Weil, A., ‘Remarques sur un mémoire d’Hermite’, Arch. Math. (Basel) 5 (1954) 197–202.CrossRefGoogle Scholar
Weil, A., ‘Euler and the Jacobians of elliptic curves’, Arithmetic and geometry, Vol. I, Progress in Mathematics 35 (eds Artin, M. and Tate, J.; Birkhäuser, Boston, 1983) 353–359.CrossRefGoogle Scholar