Article contents
Explicit isogenies in quadratic time in any characteristic
Published online by Cambridge University Press: 26 August 2016
Abstract
Consider two ordinary elliptic curves 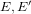 $E,E^{\prime }$ defined over a finite field
$E,E^{\prime }$ defined over a finite field 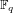 $\mathbb{F}_{q}$, and suppose that there exists an isogeny
$\mathbb{F}_{q}$, and suppose that there exists an isogeny 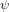 $\unicode[STIX]{x1D713}$ between
$\unicode[STIX]{x1D713}$ between 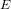 $E$ and
$E$ and 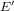 $E^{\prime }$. We propose an algorithm that determines
$E^{\prime }$. We propose an algorithm that determines  $\unicode[STIX]{x1D713}$ from the knowledge of
$\unicode[STIX]{x1D713}$ from the knowledge of 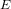 $E$,
$E$, 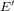 $E^{\prime }$ and of its degree
$E^{\prime }$ and of its degree  $r$, by using the structure of the
$r$, by using the structure of the 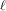 $\ell$-torsion of the curves (where
$\ell$-torsion of the curves (where 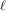 $\ell$ is a prime different from the characteristic
$\ell$ is a prime different from the characteristic  $p$ of the base field). Our approach is inspired by a previous algorithm due to Couveignes, which involved computations using the
$p$ of the base field). Our approach is inspired by a previous algorithm due to Couveignes, which involved computations using the  $p$-torsion on the curves. The most refined version of that algorithm, due to De Feo, has a complexity of
$p$-torsion on the curves. The most refined version of that algorithm, due to De Feo, has a complexity of 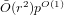 $\tilde{O} (r^{2})p^{O(1)}$ base field operations. On the other hand, the cost of our algorithm is
$\tilde{O} (r^{2})p^{O(1)}$ base field operations. On the other hand, the cost of our algorithm is 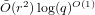 $\tilde{O} (r^{2})\log (q)^{O(1)}$, for a large class of inputs; this makes it an interesting alternative for the medium- and large-characteristic cases.
$\tilde{O} (r^{2})\log (q)^{O(1)}$, for a large class of inputs; this makes it an interesting alternative for the medium- and large-characteristic cases.
MSC classification
- Type
- Research Article
- Information
- LMS Journal of Computation and Mathematics , Volume 19 , Special Issue A: Algorithmic Number Theory Symposium XII , 2016 , pp. 267 - 282
- Copyright
- © The Author(s) 2016
References
- 4
- Cited by




