Article contents
Deterministic polynomial factoring and association schemes
Published online by Cambridge University Press: 01 April 2014
Abstract
The problem of finding a nontrivial factor of a polynomial 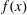 $f(x)$ over a finite field
$f(x)$ over a finite field 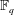 ${\mathbb{F}}_q$ has many known efficient, but randomized, algorithms. The deterministic complexity of this problem is a famous open question even assuming the generalized Riemann hypothesis (GRH). In this work we improve the state of the art by focusing on prime degree polynomials; let
${\mathbb{F}}_q$ has many known efficient, but randomized, algorithms. The deterministic complexity of this problem is a famous open question even assuming the generalized Riemann hypothesis (GRH). In this work we improve the state of the art by focusing on prime degree polynomials; let  $n$ be the degree. If
$n$ be the degree. If 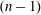 $(n-1)$ has a ‘large’
$(n-1)$ has a ‘large’  $r$-smooth divisor
$r$-smooth divisor  $s$, then we find a nontrivial factor of
$s$, then we find a nontrivial factor of 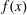 $f(x)$ in deterministic
$f(x)$ in deterministic 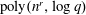 $\mbox{poly}(n^r,\log q)$ time, assuming GRH and that
$\mbox{poly}(n^r,\log q)$ time, assuming GRH and that 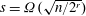 $s=\Omega (\sqrt{n/2^r})$. Thus, for
$s=\Omega (\sqrt{n/2^r})$. Thus, for 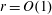 $r=O(1)$ our algorithm is polynomial time. Further, for
$r=O(1)$ our algorithm is polynomial time. Further, for 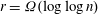 $r=\Omega (\log \log n)$ there are infinitely many prime degrees
$r=\Omega (\log \log n)$ there are infinitely many prime degrees  $n$ for which our algorithm is applicable and better than the best known, assuming GRH. Our methods build on the algebraic-combinatorial framework of
$n$ for which our algorithm is applicable and better than the best known, assuming GRH. Our methods build on the algebraic-combinatorial framework of 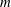 $m$-schemes initiated by Ivanyos, Karpinski and Saxena (ISSAC 2009). We show that the
$m$-schemes initiated by Ivanyos, Karpinski and Saxena (ISSAC 2009). We show that the 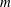 $m$-scheme on
$m$-scheme on  $n$ points, implicitly appearing in our factoring algorithm, has an exceptional structure, leading us to the improved time complexity. Our structure theorem proves the existence of small intersection numbers in any association scheme that has many relations, and roughly equal valencies and indistinguishing numbers.
$n$ points, implicitly appearing in our factoring algorithm, has an exceptional structure, leading us to the improved time complexity. Our structure theorem proves the existence of small intersection numbers in any association scheme that has many relations, and roughly equal valencies and indistinguishing numbers.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2014
References
- 3
- Cited by


