Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-20T15:11:47.970Z Has data issue: false hasContentIssue false
  • English
  • Français

Calculating conjugacy classes in Sylow 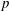$p$-subgroups of finite Chevalley groups of rank six and seven

Part of: Linear algebraic groups and related topics Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  01 April 2014

Simon M. Goodwin ,
Peter Mosch  and
Gerhard Röhrle
Simon M. Goodwin
Affiliation:
School of Mathematics, University of Birmingham, Birmingham, B15 2TT, United Kingdom email s.m.goodwin@bham.ac.uk
Peter Mosch
Affiliation:
Fakultät für Mathematik, Ruhr-Universität Bochum, D-44780 Bochum, Germany email peter.mosch@rub.de
Gerhard Röhrle
Affiliation:
Fakultät für Mathematik, Ruhr-Universität Bochum, D-44780 Bochum, Germany email gerhard.roehrle@rub.de

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 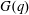$G(q)$ be a finite Chevalley group, where 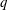$q$ is a power of a good prime 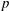$p$, and let 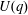$U(q)$ be a Sylow 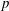$p$-subgroup of 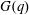$G(q)$. Then a generalized version of a conjecture of Higman asserts that the number 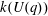$k(U(q))$ of conjugacy classes in 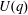$U(q)$ is given by a polynomial in 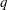$q$ with integer coefficients. In [S. M. Goodwin and G. Röhrle, J. Algebra 321 (2009) 3321–3334], the first and the third authors of the present paper developed an algorithm to calculate the values of 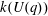$k(U(q))$. By implementing it into a computer program using 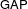$\mathsf{GAP}$, they were able to calculate 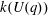$k(U(q))$ for 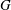$G$ of rank at most five, thereby proving that for these cases 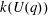$k(U(q))$ is given by a polynomial in 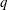$q$. In this paper we present some refinements and improvements of the algorithm that allow us to calculate the values of 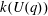$k(U(q))$ for finite Chevalley groups of rank six and seven, except 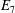$E_7$. We observe that 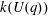$k(U(q))$ is a polynomial, so that the generalized Higman conjecture holds for these groups. Moreover, if we write 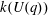$k(U(q))$ as a polynomial in 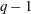$q-1$, then the coefficients are non-negative.

Under the assumption that 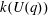$k(U(q))$ is a polynomial in 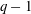$q-1$, we also give an explicit formula for the coefficients of 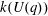$k(U(q))$ of degrees zero, one and two.

MSC classification

Secondary: 20G40: Linear algebraic groups over finite fields 20E45: Conjugacy classes
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 17 , Issue 1 , 2014 , pp. 109 - 122
Copyright
© The Author(s) 2014 

References

Alperin, J. L., ‘Unipotent conjugacy in general linear groups’, Comm. Algebra 34 (2006) 889–891.CrossRefGoogle Scholar
André, C. A. M., ‘Basic characters of the unitriangular group (for arbitrary primes)’, Proc. Amer. Soc. 130 (2002) 1943–1954.Google Scholar
Bosma, W., Cannon, J. and Playoust, C., ‘The Magma algebra system. I. The user language’, J. Symbolic Comput. 24 (1997) 235–265.Google Scholar
Bradley, J. D. and Goodwin, S. M., ‘Conjugacy classes in Sylow p-subgroups of finite Chevalley groups in bad characteristic’, Comm. Algebra (2013) to appear, arXiv:1201.1381.Google Scholar
Bürgstein, H. and Hesselink, W. H., ‘Algorithmic orbit classification for some Borel group actions’, Comp. Math. 61 (1987) 3–41.Google Scholar
Evseev, A., ‘Reduction for characters of finite algebra groups’, J. Algebra 325 (2011) 321–351.CrossRefGoogle Scholar
The GAP group, ‘GAP—groups, algorithms, and programming, version 4.3’, 2002,http://www.gap-system.org.Google Scholar
Goodwin, S. M., ‘Relative Springer isomorphisms’, J. Algebra 290 (2005) 266–281.CrossRefGoogle Scholar
Goodwin, S. M., ‘On the conjugacy classes in maximal unipotent subgroups of simple algebraic groups’, Transform. Groups 11 (2006) 51–76.Google Scholar
Goodwin, S. M., ‘Counting conjugacy classes in Sylow p-subgroups of Chevalley groups’, J. Pure Appl. Algebra 210 (2007) 201–218.CrossRefGoogle Scholar
Goodwin, S. M. and Röhrle, G., ‘Calculating conjugacy classes in Sylow p-subgroups of finite Chevalley groups’, J. Algebra 321 (2009) 3321–3334.CrossRefGoogle Scholar
Goodwin, S. M. and Röhrle, G., ‘Rational points on generalized flag varieties and unipotent conjugacy in finite groups of Lie type’, Trans. Amer. Math. Soc. 361 (2009) 177–206.Google Scholar
Goodwin, S. M. and Röhrle, G., ‘Counting conjugacy classes in the unipotent radical of parabolic subgroups of ${\rm GL}_n(q)$ ’, Pacific J. Math. 245 (2010) 47–56.Google Scholar
Greuel, G.-M., Pfister, G. and Schönemann, H., ‘Singular 3-1-1. A computer algebra system for polynomial computations’, Centre for Computer Algebra, University of Kaiserslautern, 2009, http://www. singular.uni-kl.de.CrossRefGoogle Scholar
Higman, G., ‘Enumerating $p$ -groups. I. Inequalities’, Proc. Lond. Math. Soc. (3) 10 (1960) 24–30.Google Scholar
Himstedt, F. and Huang, S., ‘Character table of a Borel subgroup of the Ree groups $\mbox{}^2F_4(q^2)$ ’, LMS J. Comput. Math. 12 (2009) 1–53.Google Scholar
Himstedt, F., Le, T. and Magaard, K., ‘Characters of the Sylow $p$ -subgroups of the Chevalley groups $D_4(p^n)$ ’, J. Algebra 332 (2011) 414–427.CrossRefGoogle Scholar
Humphreys, J. E., Introduction to Lie algebras and representation theory , Graduate Texts in Mathematics 9 (Springer, New York, 1973).Google Scholar
Isaacs, I. M., ‘Counting characters of upper triangular groups’, J. Algebra 315 (2007) 698–719.Google Scholar
Le, T., ‘Counting irreducible representations of large degree of the upper triangular groups’, J. Algebra 324 (2010) 1803–1817.Google Scholar
Lehrer, G. I., ‘Discrete series and the unipotent subgroup’, Compositio Math. 28 (1974) 9–19.Google Scholar
Robinson, G. R., ‘Counting conjugacy classes of unitriangular groups associated to finite-dimensional algebras’, J. Group Theory 1 (1998) 271–274.Google Scholar
Vera-López, A. and Arregi, J. M., ‘Conjugacy classes in unitriangular matrices’, Linear Algebra Appl. 370 (2003) 85–124.Google Scholar