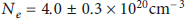1. Introduction
Research into the matter under extreme conditions represents a frontier of experimental and theoretical techniques and requires infrastructure at the most technologically advanced level. Currently, a number of laser and particle beam facilities are operating, or are under construction and nearing completion. The most prominent example presently is the National Ignition Facility (NIF, Livermore, California), where next to stockpile stewardship issues, the physics of inertial confinement fusion is addressed [Reference Nilsen, Kritcher and Martin1]. In Europe, a network of laser facilities providing infrastructure for extreme light is operational [Reference Tanaka, Spohr and Balabanski2]. In China, the laser fusion center in Mianyang is an example that in this context we want to refer to [Reference Wang, Jiang and Ding3]. The highest level of energy concentration in space and time is currently achieved with laser light. In many standard approaches to high energy density physics experiments, low entropy laser radiation is transformed into high entropy thermal radiation, and the experimental method that we present here uses just this method. A power reactor for fusion energy requires a high-efficiency driver. For experiments to study basic physics phenomena of high energy density, the driver efficiency is of less, or of no concern. Lasers, like the one used at the National Ignition Facility, do not meet the efficiency requirements for inertial fusion energy. They start with 422 MJ stored in capacitor banks to produce less than 2 MJ of Fusion power. Therefore, particle beams to induce high energy density in the matter should not be ignored [Reference Sharkov, Hoffmann, Golubev and Zhao4, Reference Zhao, Yang and Jia5], since the efficiency to convert electric power into kinetic energy of an ion may well be over 20% [Reference Böhne, Hofmann and Kessler6, Reference Hofmann7]. Laser and particle beams, as well as pulsed power devices, are important tools to generate matter under extreme conditions. Here we discuss a method that is particularly suited to produce conditions, as they prevail in stellar atmospheres and allow high-resolution spectroscopy as well as the measurement of transport properties and energy loss of ions in this environment.
Most experiments dealing with laser-plasma interaction and associated plasma phenomena use direct laser irradiation of the target (see recent examples [Reference Hornung, Zobus and Roeder8–Reference Frank, Blazevic and Grande11]). In these experiments, steep gradients in pressure, density, and temperature and strong time dependence are unavoidable and reduce the precision of the obtained data, and require detailed simulation analysis. Laser speckles, which are caused by the coherent nature of laser light propagating through the glass surfaces of the laser system, are an additional source of inhomogeneous target irradiation. This effect can be mitigated by two-sided irradiation of the target foil, and it was applied to increase the precision of energy loss measurements in experiments at GSI-Darmstadt [Reference Frank, Blazevic and Bagnoud12, Reference Cayzac, Frank and Ortner13], where two laser systems PHELIX [Reference Neumayer, Bock and Borneis14] and nhelix [Reference Schaumann, Schollmeier and Rodriguez-Prieto15] are available. In these experiments, the experimental data and two-dimensional simulation of the free electron density demonstrated that the nonuniformities were strongly reduced. However, in this case, plasma properties can only be analyzed by spectroscopic methods up to the critical density of the applied diagnostic laser. The warm dense matter part of the target is still terra incognita and must be addressed by simulation.
An alternative method is to use low-density foam targets in open geometry or encapsulated in a millimeter size hohlraum, which is heated by thermal radiation generated in an attached hohlraum. This method was pioneered at GSI-Darmstadt by Rosmej et al. and is documented in many publications [Reference Rosmej, Bagnoud and Eisenbarth16–Reference Rosmej, Suslov and Martsovenko18]. Since in this laboratory there is a long tradition to investigate the stopping power of ionized matter for heavy ions, the available wealth of energy loss data can in turn be used to deduce plasma density and plasma properties with ns resolution [Reference Belyaev, Basko and Cherkasov19–Reference Xu, Barriga-Carrasco and Blazevic22]. In summary, the technique to indirectly heat foam targets with broadband thermal radiation is well established. Besides, high precision experiments require to have as much uniformity as possible. The method we describe here is characterized by superior properties with respect to target uniformity, scale length, negligible electromagnetic field effect, and lifetime [Reference Rosmej, Bagnoud and Eisenbarth16–Reference Rosmej, Suslov and Martsovenko18, Reference Ren, Deng and Qi23], as compared with the direct laser heating method [Reference Hornung, Zobus and Roeder8–Reference Frank, Blazevic and Grande11, Reference Mackinnon, Patel and Town24, Reference Sarri, Macchi and Cecchetti25]. The prize to pay is the lower plasma temperature that can be achieved. For the experiments we had in mind [Reference Ren, Deng and Qi23, Reference Ma, Ren and Wang26], it was however just the right regime.
2. Description of the Experiment
The experiment was carried out at the XG-III laser facility of the Laser Fusion Research Center in Mianyang [Reference Su, Zhu and Xie27]. The envisioned experiments required a homogeneous plasma with well-characterized parameters. Therefore, we decided to heat a foam CHO target by laser-generated hohlraum radiation in the soft X-ray regime, to take advantage of the aforementioned properties [Reference Rosmej, Bagnoud and Eisenbarth16–Reference Rosmej, Suslov and Martsovenko18]. In our setup (see Figure 1), the foam target is attached to the open lower end of the hohlraum.

Figure 1: Geometry of the setup. The target consists of TCA foam attached to the lower side of the cylindrical Au-hohlraum. The foam and the hohlraum were supported by a stainless-steel holder. There are two free surfaces perpendicular to the blue-dashed arrow for diagnostics. The flat-field grating spectrometer (FGS) was obliquely positioned toward the backside of the foam target to measure the plasma radiation. Thus, the hohlraum radiation was effectively shielded. The X-ray diode (XRD), as well as the transmission grating spectrometer (TGS), with a single-order diffraction grating was directed toward the laser entrance hole to measure the hohlraum radiation. The pinhole (PH) camera was aimed at about 50° relative to the X-axis to image the expansion of hohlraum and foam plasma emitted from the laser entrance hole and the free surface of the foam target in the direction of X axis, respectively.
According to previous experiments, there is a time window of about 15 ns (from 5 ns to 20 ns after the onset of the laser pulse). Within this period, the target temperature is rising without substantial expansion of the bulk material. The voids of the foam sample are filled by the expanding material and in good approximation, the line density stays constant. Therefore, the target may be considered quasistatic. As an improvement to previous work, we also diagnosed the hohlraum conditions with a single-order diffraction grating spectrometer [Reference Wei, Chen and Wang28], to exclude the influence of high-order diffraction.
In Figure 1, we present an outline of the irradiation scheme and the target coupling to the hohlraum. A cylinder made from steel constitutes the hohlraum with ∼1 mm in diameter and ∼1.8 mm in height. The inner hohlraum wall was gold-coated since high Z material ensures a high diffusive resistivity of the inner wall for thermal X-rays. The open entrance hole for heating ns laser is situated at a height of ∼1.2 mm with a diameter of ∼0.6 mm. Depending on the laser parameters, the efficient conversion of laser light into hohlraum thermal soft X-rays in the temperature regime between 10 and 100 eV can be achieved [Reference Faik, Tauschwitz and Basko17], and from the previous results [Reference Rosmej, Bagnoud and Eisenbarth16], the conversion efficiency of laser energy into hohlraum X-rays reaches 17%.
The foam target consists of tri-cellulose acetate (TCA, C9H16O8). It is a very low-density material with a mass density of
![]() and a total thickness of 1 mm. It is attached to the lower end of the hohlraum cylinder and mounted to a stainless-steel holder. This sample was selected since its composition promised to reproduce the atmospheric conditions of a peculiar white dwarf (H1504 + 65 see [Reference Ma, Ren and Wang26]) when turned into a plasma. Moreover, the hydrodynamic time scale for expansion is slow and thus favorable for experiments. Simulation results indicate a hydro-response time in the ns regime and the foam starts to expand visibly about 20 ns after the onset of the laser pulse. Due to the large penetration depth of soft X-rays, quasi-isochoric heating is achieved. Once heated by soft X-rays from hohlraum radiation, the material expansion occurs inside the target between the sponge-like structures, and this micro expansion leads to target homogenization. The unique property of a foam target with respect to its temporal evolution is mainly due to the supersonic propagation character of the generated radiation heat wave. Thus, the plasma stays at its initial average density during the heating process, and the radiation energy transfer is much faster than the thermal expansion of the plasma [Reference Rosmej, Bagnoud and Eisenbarth16–Reference Rosmej, Suslov and Martsovenko18]. The simulation [Reference Faik, Tauschwitz and Basko17] shows that the foam layer becomes homogeneous and the temperature reaches the maximum at about 3–4 ns after the start of the ns laser irradiation. Later, at 10–25 ns, the foam remains at a rather flat density and temperature distribution.
and a total thickness of 1 mm. It is attached to the lower end of the hohlraum cylinder and mounted to a stainless-steel holder. This sample was selected since its composition promised to reproduce the atmospheric conditions of a peculiar white dwarf (H1504 + 65 see [Reference Ma, Ren and Wang26]) when turned into a plasma. Moreover, the hydrodynamic time scale for expansion is slow and thus favorable for experiments. Simulation results indicate a hydro-response time in the ns regime and the foam starts to expand visibly about 20 ns after the onset of the laser pulse. Due to the large penetration depth of soft X-rays, quasi-isochoric heating is achieved. Once heated by soft X-rays from hohlraum radiation, the material expansion occurs inside the target between the sponge-like structures, and this micro expansion leads to target homogenization. The unique property of a foam target with respect to its temporal evolution is mainly due to the supersonic propagation character of the generated radiation heat wave. Thus, the plasma stays at its initial average density during the heating process, and the radiation energy transfer is much faster than the thermal expansion of the plasma [Reference Rosmej, Bagnoud and Eisenbarth16–Reference Rosmej, Suslov and Martsovenko18]. The simulation [Reference Faik, Tauschwitz and Basko17] shows that the foam layer becomes homogeneous and the temperature reaches the maximum at about 3–4 ns after the start of the ns laser irradiation. Later, at 10–25 ns, the foam remains at a rather flat density and temperature distribution.
We used an ns laser pulse of 2 ns with a total pulse energy of 150 J. The beam was focused onto the open entrance hole under 45° to irradiate the wall of the gold converter. The generated soft X-ray flux subsequently irradiated and heated the foam target to the plasma state with the characteristic properties of being homogeneous, long-lived, large scale, and quasistatic. The plasma diagnostic equipment includes different tools to measure the radiative characteristics of the hohlraum and foam target. The transmission grating spectrometer (TGS), outfitted with a single-order diffraction grating (1000 lines per mm) and a slit of 100 μm, is coupled to a charge-coupled device (CCD) for the measurement of the gold hohlraum radiation. This has the advantage of significantly filtering the high-order components with moderate diffraction efficiency both in the visible light and soft X-ray regions, as well as the extreme ultraviolet regions [Reference Liu, Zhu and Gao29]. The high-resolution flat-field grating spectrometer (FGS), with a grating of 1200 lines per mm, coupled to an image plate (BAS-IP TR 2025 of FUJI IMAGING PLATE) was used to record the emission spectra of CHO plasma. A detailed analysis of the image plate sensitivity is given in ref [Reference Meadowcroft, Bentley and Stott30], and the response was taken into account in the reconstruction of the emission spectra. The X-ray diode (XRD) with Au cathode covering Ti filter was used for the time-resolved measurement of the soft X-ray flux generated in the Au-hohlraum below 400 eV with a temporal resolution of 100 ps, and the pinhole camera (PH) was used to characterize the gold hohlraum plasma and the resulting plasma.
3. Results and Discussion
3.1. Plasma Generation and Measurement of Radiative Properties
Since the heating process of the foam sample is determined by the properties of the soft X-ray flux from the hohlraum converter, the characterization of the hohlraum X-ray radiation is a necessary first step, the result is shown in Figure 2(a). The duration and amplitude of the soft X-ray signal indicate that the effective heating time of the X-rays is about 6 ns for the 2 ns/150 J laser pulse. The pinhole camera shown in the experimental setup of Figure 1 was fitted with a calibrated Fuji image plate and served to take an X-ray image of both the ionized foam plasma and the hohlraum radiation. Since the pinholes are not covered by any filters and all photons within the response range of the image plate are collected. The pinhole images are presented in Figure 2(b).

Figure 2: (a) The duration of the converter radiation pulse recorded by the X-ray diode is 5–7 ns; (b) the image of the pinhole camera with the outer features of the target geometry from the side at an angle of about 50° with respect to the X-axis.
The X-ray spectrum (see Figure 3, red line) emitted from the hohlraum was measured with a transmission grating spectrometer (TGS) coupled with a single-order diffraction grating to effectively exclude the influence of high-order diffraction. The blue line in Figure 3 is a black body radiation fit to the X-ray spectrum corresponding to a radiation temperature of 20 eV. The deviation from the black body radiation spectrum is mainly due to contributions from the radiation from the gold hohlraum.

Figure 3: Measured spectrum of the gold hohlraum. (a) Raw spectra of the hohlraum radiation recorded by TGS and (b) the reconstructed spectral distribution of the 20-eV black body radiation curve.
3.2. The Plasma Diagnostic
Figure 4 shows the high-resolution emission spectrum emitted from the foam target turned into plasma. In general, the energy of free electrons is described by a distribution. In the ideal case of thermal equilibrium, it is a Maxwell–Boltzmann distribution. Therefore, a continuous spectrum is emitted, originating from “free-bound” and “free-free” transitions, constituting the Bremsstrahlung background. Electronic transitions between ionic or atomic energy levels, so-called “bound-bound” transitions, are the origin of isolated ionic or atomic emission lines. The measured spectrum, therefore, is a superposition of isolated emission lines and a continuous background and contains a wealth of physical information due to the complex atomic processes and structures of plasma [Reference Zhao, Zhang and Cheng31, Reference Ciricosta, Vinko and Chung32].

Figure 4: Plasma emission spectra are dominated by oxygen lines. Here the continuous radiation background is already subtracted. The intensity was normalized at the maximum value, and the main lines were denoted by wavelength and transition.
The resonant lines of helium-like carbon ions (4.025 nm, 1s-2p) dominate the short-wavelength part of the spectrum, while at the long-wavelength position, Beryllium-like (62.973 nm, 2s-2p) and Boron-like (55.450 nm, 2s-2p) oxygen ions emerge. Some well-resolved and high-intensity characteristic lines in the middle-wavelength range were selected as wavelength references, such as 15.032 nm (OVI 2s-3p), 17.320 nm (O VI 2p-3d), and 19.253 nm (O V 2p-3d), which were also selected in previous projects for spectral lines identification [Reference Del Zanna, Dere, Young and Landi33–Reference Träbert, Beiersdorfer, Brickhouse and Golub35]. According to the wavelength and intensity data provided by the National Institute of Standards and Technology (NIST) database [Reference Kramida, Ralchenko and Reader36], the experimental lines, both well-resolved and some blended lines, were well-identified for the ion species and charge states. In our experiments, the spectral lines were mainly attributed to the transitions of 2s-np, 2p-ns, 2p-np, and 2p-nd (n = 2–6) for O III-VI and C IV-V ions, which are induced by L-shell ionization processes of carbon and oxygen. This indicates that the free plasma electrons originate mainly from the ionization processes of valence electrons.
The flat-field grating spectrometer was calibrated with the Hefei Synchrotron Radiation Light Source [Reference Zhongmou37, Reference Wei-Min, Lin and Guang-Yao38]. The wavelength accuracy is about 0.003 nm [Reference Du, Shen, Li, An, Shi and Wang39]. The wavelength resolution depends on the photon energy E, and we achieved E/ΔE∼300 at E = 62 eV or equivalently at a photon wavelength of 20 nm. There is an intensity uncertainty of about 11% according to the calibration of the sensitivity curve for the Typhoon FLA 7000 imaging plate scanner. This includes 10% uncertainties due to experimental conditions, such as the instability of the light source and scanner system, the spatial roughness of the imaging plate, and 5% uncertainties for the calculation of electron numbers [Reference Lu, Li and Wen40, Reference Williams, Maddox, Chen, Kojima and Millecchia41].
The relative intensity of emission lines with the same lower level is very sensitive to the electron temperature Te and density ne. Therefore, the intensity ratio of characteristic lines is a useful tool for diagnosing the plasma parameters. Assuming that the conditions for Boltzmann distribution of the upper levels are met, the radiation intensity Imn when an electron transits from energy level m to level n, can be expressed as:
![]() , where N,
gm, Am hν,
, where N,
gm, Am hν,
![]() , and k, are the total number of atoms, statistical weight, transition probability, photon energy, excited level energy, and the Boltzmann constant, respectively. Tex is the excitation temperature. This shows the obvious dependence on the temperature Tex and the weak dependence on electron density. When the conditions of local thermodynamic equilibrium (LTE) are fulfilled (the excitation temperature is equal to the electron temperature), the relative emission intensity and excitation temperature satisfies [Reference Shaikh, Hafeez, Rashid, Mahmood and Baig42]:
, and k, are the total number of atoms, statistical weight, transition probability, photon energy, excited level energy, and the Boltzmann constant, respectively. Tex is the excitation temperature. This shows the obvious dependence on the temperature Tex and the weak dependence on electron density. When the conditions of local thermodynamic equilibrium (LTE) are fulfilled (the excitation temperature is equal to the electron temperature), the relative emission intensity and excitation temperature satisfies [Reference Shaikh, Hafeez, Rashid, Mahmood and Baig42]:
where U (T) is the partition function and λmn is the transition wavelength.
This equation indicates that
![]() is proportional to the upper level energy Em for the same atom or ion lines, and the slope is
is proportional to the upper level energy Em for the same atom or ion lines, and the slope is
![]() , which contains the temperature information of the plasma. Therefore, the temperature can be obtained without detailed knowledge of the total density of atoms or the atomic species partition function.
, which contains the temperature information of the plasma. Therefore, the temperature can be obtained without detailed knowledge of the total density of atoms or the atomic species partition function.
In our experiments, the transition lines at 13.178 nm (2p-5p), 14.705 nm (2s−4p), 19.253 nm (2p-3d), 20.240 nm (2p-3d), 22.742 nm (2p-3s), and 23.130 nm (2p-3d) for O V ions and some spectral lines of O IV ions were used, respectively, for the determination of the electron temperature, they are labeled in Figure 4 along with the calibrated lines and main carbon transitions. These lines are well resolved, the transition probabilities used here are provided by the NIST database [Reference Kramida, Ralchenko and Reader36] with a well-known uncertainty. The wavelengths, degeneracies, and transition probabilities of these oxygen lines are summarized in Table 1.
Table 1: Spectroscopic parameters of the observed oxygen lines for plasma temperature determination.

Boltzmann plots were constructed from the relative intensity of oxygen lines as shown in Figure 5. The experimental data were fitted by least-squares regression. The linear coefficient of regression r turned out to be r > 0.9 on average. As a result, the plasma temperature is 16.6 and 17.2 eV obtained from O V and O IV ions, respectively.

Figure 5: Results of plasma temperature. (a, b) The O V characteristic lines (arrows) that were used to construct the Boltzmann plot. Intensities were obtained by line fitting procedure with Gaussian line profiles, and the O IV lines can be treated similarly. (c) Boltzmann plots for O IV and O V emission lines.
The validity of the local thermodynamic equilibrium assumption (LTE) was checked using McWhirter’s criterion [Reference Martino and D’Angelo43, Reference Mal, Junjuri, Gundawar and Khare44], which requires the electron number density to satisfy the conditions:
![]() , where
, where
![]() is the electron number density, T(K) is the plasma temperature, and ΔE (eV) is the difference in the energies between the upper and lower states of all investigated transitions. With the evaluated temperature of 190 000 K in our experiment and
is the electron number density, T(K) is the plasma temperature, and ΔE (eV) is the difference in the energies between the upper and lower states of all investigated transitions. With the evaluated temperature of 190 000 K in our experiment and
![]() , the maximum energy gap ΔE at 14.705 nm, and the LTE requirements are met. The determination of the electron density will be discussed later in this section.
, the maximum energy gap ΔE at 14.705 nm, and the LTE requirements are met. The determination of the electron density will be discussed later in this section.
Furthermore, the plasma is optically thin for most lines, as checked from the absorption coefficient due to inverse Bremsstrahlung [Reference Knudtson, Green and Sutton45] and the effect of self-absorption [Reference Shaikh, Rashid, Hafeez, Jamil and Baig46]. In our experiment, the maximum absorption coefficient for inverse Bremsstrahlung is 0.057 cm−1 at 28.596 nm, since the plasma diameter is a millimeter, the weak absorption (
![]() ) due to inverse Bremsstrahlung does not affect our quantitative spectroscopy. For the optically thick lines of transitions to the ground state 1s22p2, the intensities were modified according to the self-absorption coefficient.
) due to inverse Bremsstrahlung does not affect our quantitative spectroscopy. For the optically thick lines of transitions to the ground state 1s22p2, the intensities were modified according to the self-absorption coefficient.
For the uncertainty associated with the temperature obtained from the observed emission intensity, there are a number of factors that contribute to it. The main error of the Boltzmann-plot method arises from the uncertainty of the transition probability and the measurement error of the experimental spectral intensity. In our experiment, the transition probability accuracy of the spectral lines chosen for the evaluation is ≤10% [Reference Kramida, Ralchenko and Reader36], combined with the measured intensity error, the uncertainty caused by relative intensity, fitting, and transition probability is about 18%.
It should be noted that the temperature obtained by the Boltzmann-plot method is the time average temperature of the entire plasma [Reference Shaikh, Hafeez, Rashid, Mahmood and Baig42]. The spatial distribution and temporal evolution of the plasma density and temperature at different times can be obtained by hydrodynamic simulations [Reference Rosmej, Suslov and Martsovenko18]. With a similar experimental design, the plasma temperature variation is estimated to be about 25% during the 5 to 20 ns time span. These uncertainties, however, do not cause directly similar uncertainty in the temperature determination. The relative uncertainty in the electron temperature determination by the Boltzmann-plot method scales with the factor T/Em, which is the ratio of the thermal energy of the plasma T and the level energy Em. As a result, we have estimated that our plasma temperature relative error is about 7%.
Also from previous experiments [Reference Rosmej, Suslov and Martsovenko18], it is well documented that foam layers show high hydrodynamic stability during the heating process. The matter density is almost constant and stays close to the initial line density value. As a result of this, the radiative heat wave is supersonic. Thus, the radiative heat transfer proceeds at a higher speed than the thermal expansion.
Calculation of the ion charge state distributions using the collisional radiative code FLYCHK [Reference Lee, Chen, Morgan and Chung47] shows that the ionization degree of CHO foam is around
![]() for the 16.8 ± 1.1 eV electron temperature that we obtained from the Boltzmann-plot method and the corresponding free electron density of
for the 16.8 ± 1.1 eV electron temperature that we obtained from the Boltzmann-plot method and the corresponding free electron density of
![]() . Here the relative error is 7%. The mean ion charge state
. Here the relative error is 7%. The mean ion charge state
![]() is q = 2-3.
is q = 2-3.
4. Conclusions
In our experimental campaign, we used a foam target (TCA) and subjected it to broadband thermal soft X-ray radiation generated in an attached cylindrical hohlraum. The resulting plasma is characterized by a large volume with high uniformity and long lifetime and near-critical density of free electrons of
![]() and a temperature of 16.8 ± 1.1 eV. We applied high-resolution spectroscopy to determine the hohlraum and plasma characteristics. We used a single-order diffraction grating and flat-field grating spectrometer. In addition, the spectroscopy and Boltzmann-plot method were successfully used for the diagnosis of plasma temperature by analyzing time-averaged emission spectra. The free electron density was determined based on the ionization degree and electronic structure information of the CHO plasma. Moreover, the plasma is a good test bed for laser-NCD (near-critical density) plasma interaction to generate high energy and brilliant charged particle and photon beams.
and a temperature of 16.8 ± 1.1 eV. We applied high-resolution spectroscopy to determine the hohlraum and plasma characteristics. We used a single-order diffraction grating and flat-field grating spectrometer. In addition, the spectroscopy and Boltzmann-plot method were successfully used for the diagnosis of plasma temperature by analyzing time-averaged emission spectra. The free electron density was determined based on the ionization degree and electronic structure information of the CHO plasma. Moreover, the plasma is a good test bed for laser-NCD (near-critical density) plasma interaction to generate high energy and brilliant charged particle and photon beams.
Data Availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Authors’ Contributions
Yongtao Zhao initiated and organized the experiments. Jieru Ren and Yongtao Zhao carried out the experiments together with the high-power laser team (Zongqing Zhao, Weimin Zhou, and Yuqiu Gu), the plasma diagnostics team, including the XRD team (Zhurong Cao, Xing Wang, Lirong Liu, and Bo Cui), the Flat Field Grating Spectrometer team (Shaoyi Wang, Bubo Ma, Yong Chen, and Leifeng Cao), the Transmission Grating Spectrometer team (Quanping Fan, Bubo Ma, Yong Chen, and Leifeng Cao) as well as the experimental setup installation and collimation team (Zhigang Deng, Wei Qi, Rui Cheng, Wenqing Wei, Xing Xu, Wei Liu, Shuai Yin, Jianhua Feng, Zhongmin Hu, and Hao Xu). Bubo Ma, Shaoyi Wang, Quanping Fan, and Jieru Ren analyzed the spectral data. Benzheng Chen, Shizheng Zhang, Zhongfeng Xu, Fangfang Li, Taotao Li, Yutian Li, Yingying Wang, Quanxi Xue, Yongtao Zhao, and Dieter Hoffmann contributed to the physical interpretation of experimental data. Bubo Ma, Jieru Ren, Yongtao Zhao, and Dieter Hoffmann drafted the article and all the coauthors revised the manuscript critically. Zhigang Deng, Wei Qi, Rui Cheng, Wenqing Wei, Xing Xu, Wei Liu, Shuai Yin, Jianhua Feng, Zhongmin Hu, Hao Xu, Zongqing Zhao, Weimin Zhou, and Yuqiu Gu made a critical revision to the experimental setup section and improved Figure 1. Zhurong Cao, Xing Wang, Lirong Liu, and Bo Cui made a critical revision in discussions related to Figure 2(a). Jieru Ren, Zhigang Deng, Wei Qi, and Wenqing Wei made critical modifications in discussions related to Figure 2(b). Quanping Fan, Bubo Ma, Yong Chen, and Leifeng Cao made a critical revision in discussions related to Figure 3. Shaoyi Wang, Yong Chen, and Leifeng Cao performed the design and calibration of the spectrometers and made a critical revision in discussions related to Figure 4. Benzheng Chen, Shizheng Zhang, Zhongfeng Xu, Fangfang Li, Taotao Li, Yutian Li, Yingying Wang, and Quanxi Xue made a critical revision in discussions related to the temperature determination. All the authors approved the final version to be published and agreed to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Acknowledgments
The experiment was performed at the XG-III facility in Mianyang. The authors are grateful to the staff of Laser Fusion Research Center. The work was supported by National Key R&D Program of China, No. 2019YFA0404900, Chinese Science Challenge Project, No. TZ2016005, National Natural Science Foundation of China (Grant Nos. U2030104, 12120101005, 12175174, and 11975174), China Postdoctoral Science Foundation (Grant no. 2017M623145), State Key Laboratory Foundation of Laser Interaction with Matter (Nos. SKLLIM1807 and SKLLIM2106), and the Fundamental Research Funds for the Central Universities.