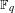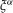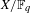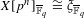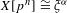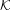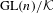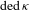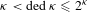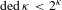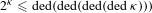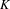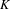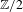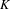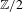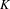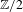Research Article
LOCAL INTERDEFINABILITY OF WEIERSTRASS ELLIPTIC FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 24 November 2014, pp. 673-691
-
- Article
- Export citation
THE DISTRIBUTION OF TORSION SUBSCHEMES OF ABELIAN VARIETIES
- Part of:
-
- Published online by Cambridge University Press:
- 15 December 2014, pp. 693-710
-
- Article
- Export citation
WHITTAKER PERIODS, MOTIVIC PERIODS, AND SPECIAL VALUES OF TENSOR PRODUCT
 $L$-FUNCTIONS
$L$-FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 31 March 2015, pp. 711-769
-
- Article
-
- You have access
- Export citation
ON THE NUMBER OF DEDEKIND CUTS AND TWO-CARDINAL MODELS OF DEPENDENT THEORIES
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 771-784
-
- Article
- Export citation
CENTER MANIFOLDS FOR PARTIALLY HYPERBOLIC SETS WITHOUT STRONG UNSTABLE CONNECTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 11 March 2015, pp. 785-828
-
- Article
-
- You have access
- Export citation
EQUIVARIANT CALCULUS OF FUNCTORS AND
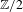 $\mathbb{Z}/2$-ANALYTICITY OF REAL ALGEBRAIC
$\mathbb{Z}/2$-ANALYTICITY OF REAL ALGEBRAIC 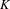 $K$-THEORY
$K$-THEORY
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2015, pp. 829-883
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
JMJ volume 15 Issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 14 September 2016, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
JMJ volume 15 Issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 14 September 2016, pp. b1-b7
-
- Article
-
- You have access
- Export citation