Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gillet, Henri
Gorchinskiy, Sergey
and
Ovchinnikov, Alexey
2013.
Parameterized Picard–Vessiot extensions and Atiyah extensions.
Advances in Mathematics,
Vol. 238,
Issue. ,
p.
322.
Ovchinnikov, Alexey
2014.
Difference integrability conditions for parameterized linear difference and differential equations.
Advances in Applied Mathematics,
Vol. 53,
Issue. ,
p.
61.
Arreche, Carlos E.
2014.
Computation of the unipotent radical of the differential Galois group for a parameterized second-order linear differential equation.
Advances in Applied Mathematics,
Vol. 57,
Issue. ,
p.
44.
Gorchinskiy, Sergey
and
Ovchinnikov, Alexey
2014.
Isomonodromic differential equations and differential categories.
Journal de Mathématiques Pures et Appliquées,
Vol. 102,
Issue. 1,
p.
48.
Minchenko, Andrey
Ovchinnikov, Alexey
and
Singer, Michael F.
2015.
Reductive Linear Differential Algebraic Groups and the Galois Groups of Parameterized Linear Differential Equations.
International Mathematics Research Notices,
Vol. 2015,
Issue. 7,
p.
1733.
Maier, Annette
2015.
On the parameterized differential inverse Galois problem over k((t))(x).
Journal of Algebra,
Vol. 428,
Issue. ,
p.
43.
Arreche, Carlos E.
2016.
On the computation of the parameterized differential Galois group for a second-order linear differential equation with differential parameters.
Journal of Symbolic Computation,
Vol. 75,
Issue. ,
p.
25.
Mitschi, Claude
2016.
Некоторые приложения параметрической теории Пикара-Вессио.
Известия Российской академии наук. Серия математическая,
Vol. 80,
Issue. 1,
p.
177.
Mitschi, C
2016.
Some applications of parameterized Picard-Vessiot theory.
Izvestiya: Mathematics,
Vol. 80,
Issue. 1,
p.
167.
Arreche, Carlos E.
2017.
Computation of the difference-differential Galois group and differential relations among solutions for a second-order linear difference equation.
Communications in Contemporary Mathematics,
Vol. 19,
Issue. 06,
p.
1650056.
Di Vizio, Lucia
Hardouin, Charlotte
and
Wibmer, Michael
2017.
DIFFERENCE ALGEBRAIC RELATIONS AMONG SOLUTIONS OF LINEAR DIFFERENTIAL EQUATIONS.
Journal of the Institute of Mathematics of Jussieu,
Vol. 16,
Issue. 1,
p.
59.
Ovchinnikov, Alexey
and
Wibmer, Michael
2017.
Tannakian Categories With Semigroup
Actions.
Canadian Journal of Mathematics,
Vol. 69,
Issue. 3,
p.
687.
Hardouin, Charlotte
Minchenko, Andrei
and
Ovchinnikov, Alexey
2017.
Calculating differential Galois groups of parametrized differential equations, with applications to hypertranscendence.
Mathematische Annalen,
Vol. 368,
Issue. 1-2,
p.
587.
Minchenko, Andrei
and
Ovchinnikov, Alexey
2018.
Calculating Galois groups of third-order linear differential equations with parameters.
Communications in Contemporary Mathematics,
Vol. 20,
Issue. 04,
p.
1750038.
Bachmayr, Annette
2018.
New classes of parameterized differential Galois groups.
Mathematische Zeitschrift,
Vol. 288,
Issue. 1-2,
p.
361.
Di Vizio, Lucia
2019.
Action of an endomorphism on (the solutions of) a linear differential equation.
Publications mathématiques de Besançon. Algèbre et théorie des nombres,
p.
21.
Wibmer, Michael
2021.
Almost-simple affine difference algebraic groups.
Mathematische Zeitschrift,
Vol. 299,
Issue. 1-2,
p.
473.
Amzallag, Eli
Minchenko, Andrei
and
Pogudin, Gleb
2021.
Degree bound for toric envelope of a linear algebraic group.
Mathematics of Computation,
Bachmayr, Annette
and
Wibmer, Michael
2022.
Algebraic groups as difference Galois groups of linear differential equations.
Journal of Pure and Applied Algebra,
Vol. 226,
Issue. 2,
p.
106854.
Arreche, Carlos E.
and
Zhang, Yi
2022.
Computing differential Galois groups of second-order linear q-difference equations.
Advances in Applied Mathematics,
Vol. 132,
Issue. ,
p.
102273.
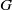 $G$ is a PPV Galois group over these fields if and only if
$G$ is a PPV Galois group over these fields if and only if 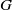 $G$ contains a Kolchin-dense finitely generated group. We show that, for a class of LDAGs
$G$ contains a Kolchin-dense finitely generated group. We show that, for a class of LDAGs 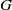 $G$, including unipotent groups,
$G$, including unipotent groups, 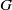 $G$ is such a group if and only if it has differential type
$G$ is such a group if and only if it has differential type 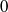 $0$. We give a procedure to determine if a parameterized linear differential equation has a PPV Galois group in this class and show how one can calculate the PPV Galois group of a parameterized linear differential equation if its Galois group has differential type
$0$. We give a procedure to determine if a parameterized linear differential equation has a PPV Galois group in this class and show how one can calculate the PPV Galois group of a parameterized linear differential equation if its Galois group has differential type 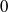 $0$.
$0$.

