Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-17T18:18:46.671Z Has data issue: false hasContentIssue false
  • English
  • Français

SUB-RIEMANNIAN RICCI CURVATURES AND UNIVERSAL DIAMETER BOUNDS FOR 3-SASAKIAN MANIFOLDS

Part of: Global differential geometry

Published online by Cambridge University Press:  21 June 2017

Luca Rizzi Open the ORCID record for Luca Rizzi [Opens in a new window]  and
Pavel Silveira
Luca Rizzi
Affiliation:
University of Grenoble Alpes, CNRS, Institut Fourier, F-38000 Grenoble, France Inria, team GECO & CMAP, École Polytechnique, CNRS, Université Paris-Saclay, Palaiseau, France (past institution) (luca.rizzi@univ-grenoble-alpes.fr)
Pavel Silveira
Affiliation:
Leibniz Universität Hannover, Institut für Analysis, Germany (psilveir@math.uni-hannover.de)
Get access Rights & Permissions [Opens in a new window]

Abstract

For a fat sub-Riemannian structure, we introduce three canonical Ricci curvatures in the sense of Agrachev–Zelenko–Li. Under appropriate bounds we prove comparison theorems for conjugate lengths, Bonnet–Myers type results and Laplacian comparison theorems for the intrinsic sub-Laplacian. As an application, we consider the sub-Riemannian structure of 3-Sasakian manifolds, for which we provide explicit curvature formulas. We prove that any complete 3-Sasakian structure of dimension 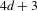$4d+3$, with 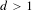$d>1$, has sub-Riemannian diameter bounded by $\unicode[STIX]{x1D70B}$. When 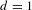$d=1$, a similar statement holds under additional Ricci bounds. These results are sharp for the natural sub-Riemannian structure on 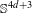$\mathbb{S}^{4d+3}$ of the quaternionic Hopf fibrations:

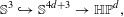$$\begin{eqnarray}\mathbb{S}^{3}{\hookrightarrow}\mathbb{S}^{4d+3}\rightarrow \mathbb{HP}^{d},\end{eqnarray}$$
whose exact sub-Riemannian diameter is $\unicode[STIX]{x1D70B}$, for all 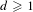$d\geqslant 1$.

Keywords

53-XX differential geometrysub-Riemannian geometry3-Sasakiancurvature

MSC classification

Primary: 53C17: Sub-Riemannian geometry 53C21: Methods of Riemannian geometry, including PDE methods; curvature restrictions 53C22: Geodesics 53C25: Special Riemannian manifolds (Einstein, Sasakian, etc.) 53C26: Hyper-Kähler and quaternionic Kähler geometry, “special” geometry
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 18 , Issue 4 , July 2019 , pp. 783 - 827
Copyright
© Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abou-Kandil, H., Freiling, G., Ionescu, V. and Jank, G., Matrix Riccati Equations: In Control and Systems Theory, Systems & Control: Foundations and Applications (Springer, NY, 2003).Google Scholar
Agrachev, A., Any sub-Riemannian metric has points of smoothness, Dokl. Akad. Nauk 424(3) (2009), 295–298.Google Scholar
Agrachev, A., Some open problems, in Geometric Control Theory and sub-Riemannian Geometry, Springer INdAM Series, Volume 5, pp. 1–13 (Springer, Cham, 2014).Google Scholar
Agrachev, A., Barilari, D. and Paoli, E., Volume geodesic distortion and Ricci curvature for Hamiltonian dynamics, Preprint, 2016.Google Scholar
Agrachev, A., Barilari, D. and Rizzi, L., Curvature: a variational approach, Mem. Amer. Math. Soc. (2015), in press.Google Scholar
Agrachev, A., Barilari, D. and Rizzi, L., Sub-Riemannian curvature in contact geometry, J. Geom. Anal. 27(1) (2017), 366–408.Google Scholar
Agrachev, A., Boscain, U., Gauthier, J.-P. and Rossi, F., The intrinsic hypoelliptic Laplacian and its heat kernel on unimodular Lie groups, J. Funct. Anal. 256(8) (2009), 2621–2655.Google Scholar
Agrachev, A. and Gamkrelidze, R. V., Feedback-invariant optimal control theory and differential geometry. I. Regular extremals, J. Dyn. Control Syst. 3(3) (1997), 343–389.Google Scholar
Agrachev, A. and Lee, P. W. Y., Generalized Ricci curvature bounds for three dimensional contact sub-Riemannian manifolds, Math. Ann. 360(1–2) (2014), 209–253.Google Scholar
Agrachev, A. and Lee, P. W. Y., Bishop and Laplacian comparison theorems on three-dimensional contact sub-Riemannian manifolds with symmetry, J. Geom. Anal. 25(1) (2015), 512–535.Google Scholar
Agrachev, A., Rizzi, L. and Silveira, P., On conjugate times of LQ optimal control problems, J. Dyn. Control Syst. 21(4) (2015), 625–641.Google Scholar
Agrachev, A. and Sachkov, Y., Control Theory From the Geometric Viewpoint, Encyclopaedia of Mathematical Sciences, Volume 87 (Springer, Berlin, 2004). Control Theory and Optimization, II.Google Scholar
Agrachev, A. and Zelenko, I., Geometry of Jacobi curves. I, J. Dyn. Control Syst. 8(1) (2002), 93–140.Google Scholar
Agrachev, A. and Zelenko, I., Geometry of Jacobi curves. II, J. Dyn. Control Syst. 8(2) (2002), 167–215.Google Scholar
Agrachev, A. A., Barilari, D. and Boscain, U., Introduction to Riemannian and sub-Riemannian geometry (Lecture Notes). http://webusers.imj-prg.fr/∼davide.barilari/notes.php, 2016.Google Scholar
Barilari, D., Boscain, U., Charlot, G. and Neel, R. W., On the heat diffusion for generic Riemannian and sub-Riemannian structures, Int. Math. Res. Not. (2016), in press.Google Scholar
Barilari, D., Boscain, U. and Neel, R. W., Small-time heat kernel asymptotics at the sub-Riemannian cut locus, J. Differential Geom. 92(3) (2012), 373–416.Google Scholar
Barilari, D. and Ivanov, S., A sub-Riemannian Bonnet–Myers theorem for quaternionic contact structures, Preprint, 2017.Google Scholar
Barilari, D. and Rizzi, L., A formula for Popp’s volume in sub-Riemannian geometry, Anal. Geom. Metr. Spaces 1 (2013), 42–57.Google Scholar
Barilari, D. and Rizzi, L., On Jacobi fields and canonical connection in sub-Riemannian geometry, Arch. Math. (Brno) 53 (2017), 77–92.Google Scholar
Barilari, D. and Rizzi, L., Comparison theorems for conjugate points in sub-Riemannian geometry, ESAIM Control Optim. Calc. Var. 22(2) (2016), 439–472.Google Scholar
Baudoin, F., Bonnefont, M. and Garofalo, N., A sub-Riemannian curvature-dimension inequality, volume doubling property and the Poincaré inequality, Math. Ann. 358(3–4) (2014), 833–860.Google Scholar
Baudoin, F., Bonnefont, M., Garofalo, N. and Munive, I. H., Volume and distance comparison theorems for sub-Riemannian manifolds, J. Funct. Anal. 267(7) (2014), 2005–2027.Google Scholar
Baudoin, F. and Garofalo, N., Curvature-dimension inequalities and Ricci lower bounds for sub-Riemannian manifolds with transverse symmetries, J. Eur. Math. Soc. 19(1) (2017), 151–219.Google Scholar
Baudoin, F. and Kim, B., The Lichnerowicz-Obata theorem on sub-Riemannian manifolds with transverse symmetries, J. Geom. Anal. 26(1) (2016), 156–170.Google Scholar
Baudoin, F., Kim, B. and Wang, J., Transverse Weitzenböck formulas and curvature dimension inequalities on Riemannian foliations with totally geodesic leaves, Comm. Anal. Geom. 24(5) (2016), 913–937.Google Scholar
Baudoin, F. and Wang, J., The subelliptic heat kernel on the CR sphere, Math. Z. 275(1–2) (2013), 135–150.Google Scholar
Baudoin, F. and Wang, J., Curvature-dimension inequalities and subelliptic heat kernel gradient bounds on contact manifolds, Potential Anal. 40 (2014), 163–193.Google Scholar
Baudoin, F. and Wang, J., The subelliptic heat kernels of the quaternionic Hopf fibration, Potential Anal. 41(3) (2014), 959–982.Google Scholar
Blair, D. E., Riemannian Geometry of Contact and Symplectic Manifolds, 2nd edn, Progress in Mathematics, Volume 203 (Birkhäuser, Boston, MA, 2010).Google Scholar
Boyer, C. P., Galicki, K. and Mann, B. M., The geometry and topology of 3-Sasakian manifolds, J. Reine Angew. Math. 455 (1994), 183–220.Google Scholar
Coron, J.-M., Control and Nonlinearity, Mathematical Surveys and Monographs, Volume 136 (American Mathematical Society, Providence, RI, 2007).Google Scholar
Eschenburg, J.-H. and Heintze, E., Comparison theory for Riccati equations, Manuscripta Math. 68(2) (1990), 209–214.Google Scholar
Gallot, S., Hulin, D. and Lafontaine, J., Riemannian Geometry, 3rd edn (Universitext. Springer, Berlin, 2004).Google Scholar
Hasegawa, I. and Seino, M., Some remarks on Sasakian geometry—applications of Myers’ theorem and the canonical affine connection, J. Hokkaido Univ. Educ. Sect. II A 32(1) (1981/82), 1–7.Google Scholar
Hladky, R. K., The topology of quaternionic contact manifolds, Ann. Global Anal. Geom. 47(1) (2015), 99–115.Google Scholar
Iliev, B. Z., Handbook of Normal Frames and Coordinates, Progress in Mathematical Physics, Volume 42 (Birkhäuser, Basel, 2006).Google Scholar
Ivanov, S., Minchev, I. and Vassilev, D., Quaternionic contact Einstein structures and the quaternionic contact Yamabe problem, Mem. Amer. Math. Soc. 231(1086) (2014), vi+82.Google Scholar
Ivanov, S., Minchev, I. and Vassilev, D., Quaternionic contact Einstein manifolds, Math. Res. Lett. 23(5) (2016), 1405–1432.Google Scholar
Ivanov, S. and Vassilev, D., The Lichnerowicz and Obata first eigenvalue theorems and the Obata uniqueness result in the Yamabe problem on CR and quaternionic contact manifolds, Nonlinear Anal.: Theory Methods Appl. 126 (2015), 262–323.Google Scholar
Jurdjevic, V., Geometric Control Theory, Cambridge Studies in Advanced Mathematics, Volume 52 (Cambridge University Press, Cambridge, 1997).Google Scholar
Kashiwada, T., On a contact 3-structure, Math. Z. 238(4) (2001), 829–832.Google Scholar
Lee, P. W. Y. and Li, C., Bishop and Laplacian comparison theorems on Sasakian manifolds, Preprint, 2013.Google Scholar
Lee, P. W. Y., Li, C. and Zelenko, I., Ricci curvature type lower bounds for sub-Riemannian structures on Sasakian manifolds, Discrete Contin. Dyn. Syst. 36(1) (2016), 303–321.Google Scholar
Li, C. and Zelenko, I., Jacobi equations and comparison theorems for corank 1 sub-Riemannian structures with symmetries, J. Geom. Phys. 61(4) (2011), 781–807.Google Scholar
Manasse, F. K. and Misner, C. W., Fermi normal coordinates and some basic concepts in differential geometry, J. Math. Phys. 4 (1963), 735–745.Google Scholar
Montgomery, R., A tour of Sub-Riemannian Geometries, their Geodesics and Applications, Mathematical Surveys and Monographs, Volume 91 (American Mathematical Society, Providence, RI, 2002).Google Scholar
Myers, S. B., Riemannian manifolds with positive mean curvature, Duke Math. J. 8 (1941), 401–404.Google Scholar
Nitta, Y., A diameter bound for Sasaki manifolds, Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 13(1) (2014), 207–224.Google Scholar
Rifford, L., Sub-Riemannian Geometry and Optimal Transport, SpringerBriefs in Mathematics (Springer, Cham, 2014). viii+140 pp.Google Scholar
Royden, H. L., Comparison theorems for the matrix Riccati equation, Comm. Pure Appl. Math. 41(5) (1988), 739–746.Google Scholar
Strichartz, R. S., Sub-Riemannian geometry, J. Differential Geom. 24(2) (1986), 221–263.Google Scholar
Strichartz, R. S., Corrections to: ‘Sub-Riemannian geometry’. J. Differential Geom. 24 (1986), no. 2, 221–263; MR0862049 (88b:53055), J. Differential Geom. 30(2) (1989), 595–596.Google Scholar
Tanno, S., Killing vectors on contact Riemannian manifolds and fiberings related to the Hopf fibrations, Tôhoku Math. J. (2) 23 (1971), 313–333.Google Scholar
Villani, C., Optimal Transport, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], Volume 338 (Springer, Berlin, 2009). Old and new.Google Scholar
Zelenko, I. and Li, C., Differential geometry of curves in Lagrange Grassmannians with given young diagram, Differential Geom. Appl. 27(6) (2009), 723–742.Google Scholar