Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-16T06:54:25.468Z Has data issue: false hasContentIssue false
  • English
  • Français

A robustly chain transitive attractor with singularities of different indices

Part of: Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  01 June 2012

Christian Bonatti ,
Ming Li  and
Dawei Yang
Christian Bonatti
Affiliation:
Institut de Mathématiques de Bourgogne, Université de Bourgogne, Dijon 21004, France (bonatti@u-bourgogne.fr)
Ming Li
Affiliation:
School of Mathematical Sciences, Nankai University, Tianjin 300071, PR China (limingmath@nankai.edu.cn)
Dawei Yang
Affiliation:
School of Mathematics, Jilin University, Changchun 130012, PR China (yangdw1981@gmail.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a 4-manifold, we build a non-empty 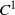${C}^{1} $-open set of vector fields having a (chain transitive) attractor containing singularities of different indices. Then, we begin the study of the hyperbolic properties of such a robust singular attractor.

Keywords

singular attractorrobustly chain transitivepartially hyperbolicindex

MSC classification

Secondary: 37D30: Partially hyperbolic systems and dominated splittings
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 12 , Issue 3 , July 2013 , pp. 449 - 501
Copyright
©Cambridge University Press 2012 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afraĭmovič, V., Bykov, V. and Shilnikov, L., The origin and structure of the Lorenz attractor, Dokl. Akad. Nauk SSSR 234 (1977), 336–339.Google Scholar
Aoki, N., The set of Axiom A diffeomorphisms with no cycles, Bol. Soc. Bras. Mat. 23 (1992), 21–65.Google Scholar
Arroyo, A. and Rodriguez Hertz, F., Homoclinic bifurcations and uniform hyperbolicity for three-dimensional flows, Ann. Inst. H. Poincaré Anal. Non Linéaire 20 (2003), 805–841.Google Scholar
Bamón, R., Kiwi, J. and Rivera, J., Wild Lorenz like attractors, preprint (2006).Google Scholar
Bonatti, C. and Crovisier, S., Récurrence et généricité, Invent. Math. 158 (1) (2004), 33–104.CrossRefGoogle Scholar
Bonatti, C. and Díaz, L., Persistent nonhyperbolic transitive diffeomorphisms, Ann. of Math. (2) 143 (1996), 357–396.CrossRefGoogle Scholar
Bonatti, C., Díaz, L. and Pujals, E., A ${C}^{1} $-generic dichotomy for diffeomorphisms: Weak forms of hyperbolicty or infinitely many sinks or sources, Ann. of Math. (2) 158 (2003), 355–418.Google Scholar
Bonatti, C., Díaz, L., Pujals, E. and Rocha, J., Robustly transitive sets and heterodimensional cycles. Geometric methods in dynamics. I, Astérisque 286 (2003), 187–222.Google Scholar
Bonatti, C., Díaz, L. and Viana, M., Discontinuity of the Hausdorff dimension of hyperbolic sets, C. R. Acad. Sci. Paris Sér. I Math. 320 (6) (1995), 713–718.Google Scholar
Bonatti, C., Gourmelon, N. and Vivier, T., Perturbations of the derivative along periodic orbits, Ergodic Theory Dynam. Systems 26 (2006), 1307–1337.CrossRefGoogle Scholar
Bonatti, C., Li, M. and Yang, D., On the existence of attractors, preprint (2008).Google Scholar
Bonatti, C. and Viana, M., SRB measures for partially hyperbolic systems whose central direction is mostly contracting, Israel J. Math. 115 (2002), 157–193.Google Scholar
Bonatti, C., Pumariño, A. and Viana, M., Lorenz attractors with arbitrary expanding dimension, C. R. Acad. Sci. Paris 325 (1997), 883–888.Google Scholar
Doering, C. I., Persistently transitive vector fields on three dimensional manifolds, Proc. on dynamical systems and bifurcation theory, Pitman Res. Notes Math. Ser. 160 (1987), 59–89.Google Scholar
Díaz, L., Pujals, E. and Ures, R., Partial hyperbolicity and robust transitivity, Acta Math. 183 (1999), 1–43.Google Scholar
Gan, S., Li, M. and Wen, L., Robustly transitive singular sets via approach of an extended linear Poincaré flow, Discrete Contin. Dyn. Syst. 13 (2005), 239–269.Google Scholar
Gan, S. and Wen, L., Nonsingular star flows satisfy Axiom A and the nocycle condition, Invent. Math. 164 (2006), 279–315.Google Scholar
Gan, S., Wen, L. and Zhu, S., Indices of singularities of robustly transitive sets, preprint (2007).Google Scholar
Guchenheimer, J., A strange, strange attractor, in The Hopf bifurcation theorems and its applications, Applied Mathematical Series, 19. pp. 368–381. (Springer-Verlag, 1976).Google Scholar
Guchenheimer, J. and Williams, R., Structural stability of Lorenz attractors, Publ. Math. Inst. Hautes Études Sci. 50 (1979), 59–72.Google Scholar
Hayashi, S., Diffeomorphisms in ${ \mathcal{F} }^{1} (M)$ satisfy Axiom A, Ergodic Theory Dyn. Syst. 12 (1992), 233–253.CrossRefGoogle Scholar
Hayashi, S., Connecting invariant manifolds and the solution of the ${C}^{1} $ stability conjecture and $\Omega $-stability conjecture for flows, Ann. of Math. (2) 145 (1997), 81–137.Google Scholar
Liao, S., On the stability conjecture, Chin. Ann. Math. 1 (1980), 9–30.Google Scholar
Lorenz, E. N., Deterministic nonperiodic flow, J. Atmospheric Sci. 20 (1963), 130–141.2.0.CO;2>CrossRefGoogle Scholar
Mañé, R., An ergodic closing lemma, Ann. of Math. (2) 116 (1982), 503–540.CrossRefGoogle Scholar
Mañé, R., A proof of the ${C}^{1} $ stability Conjecture, Publ. Math. Inst. Hautes Études Sci. 66 (1988), 161–210.Google Scholar
Metzger, R. and Morales, C., Sectional-hyperbolic systems, preprint (2005).Google Scholar
Morales, C. and Pacifico, M., A dichotomy for three-dimensional vector fields, Ergodic Theory Dynam. Systems 23 (2003), 1575–1600.Google Scholar
Morales, C., Pacifico, M. and Pujals, E., On ${C}^{1} $ robust singular transitive sets for three-dimensional flows, C. R. Acad. Sci. Paris 326 (1998), 81–86.CrossRefGoogle Scholar
Morales, C., Pacifico, M. and Pujals, E., Robust transitive singular sets for 3-flows are partially hyperbolic attractors or repellers, Ann. of Math. (2) 160 (2004), 375–432.CrossRefGoogle Scholar
Morales, C. and Pujals, E., Singular strange attractors on the boundary of Morse–Smale systems, Ann. Sci. Éc. Norm. Supér. (4) 30 (1997), 693–717.Google Scholar
Pugh, C., The closing lemma, Amer. J. Math. 89 (1967), 956–1009.CrossRefGoogle Scholar
Pujals, E. R. and Sambarino, M., Homoclinic tangencies and hyperbolicity for surface diffeomorphisms, Ann. of Math. (2) 151 (3) (2000), 961–1023.CrossRefGoogle Scholar
Shilnikov, L. P., Shilnikov, A. L., Taruve, D. V. and Chua, L. O., Methods of qualitative theory in nonlinear dynamics, World Scientific, Series A, Volume 5.Google Scholar
Vivier, T., Flots robustement transitifs sur les variétés compactes, C. R. Acad. Sci. Paris 337 (2003), 791–796.CrossRefGoogle Scholar
Wen, L., On the C1-stability conjecture for flows, J. Differential Equations 129 (1996), 334–357.Google Scholar
Wen, L., Homoclinic tangencies and dominated splittings, Nonlinearity 15 (2002), 1445–1469.Google Scholar
Wen, L., Generic diffeomorphisms away from homoclinic tangencies and heterodimensional cycles, Bull. Braz. Math. Soc. (N.S.) 35 (2004), 419–452.Google Scholar