Article contents
RIEMANN–HILBERT CORRESPONDENCE FOR MIXED TWISTOR 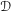 ${\mathcal{D}}$-MODULES
${\mathcal{D}}$-MODULES
Published online by Cambridge University Press: 19 May 2017
Abstract
We introduce the notion of regularity for a relative holonomic 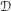 ${\mathcal{D}}$-module in the sense of Monteiro Fernandes and Sabbah [Internat. Math. Res. Not. (21) (2013), 4961–4984]. We prove that the solution functor from the bounded derived category of regular relative holonomic modules to that of relative constructible complexes is essentially surjective by constructing a right quasi-inverse functor. When restricted to relative
${\mathcal{D}}$-module in the sense of Monteiro Fernandes and Sabbah [Internat. Math. Res. Not. (21) (2013), 4961–4984]. We prove that the solution functor from the bounded derived category of regular relative holonomic modules to that of relative constructible complexes is essentially surjective by constructing a right quasi-inverse functor. When restricted to relative 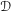 ${\mathcal{D}}$-modules underlying a regular mixed twistor
${\mathcal{D}}$-modules underlying a regular mixed twistor 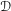 ${\mathcal{D}}$-module, this functor satisfies the left quasi-inverse property.
${\mathcal{D}}$-module, this functor satisfies the left quasi-inverse property.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press 2017
Footnotes
The research of TMF was supported by Fundação para a Ciência e Tecnologia UID/MAT/04561/2013. The research of CS was supported by the grant ANR-13-IS01-0001-01 of the Agence nationale de la recherche.
References
- 3
- Cited by


