Article contents
THE RENORMALIZED VOLUME AND UNIFORMIZATION OF CONFORMAL STRUCTURES
Published online by Cambridge University Press: 30 June 2016
Abstract
We study the renormalized volume of asymptotically hyperbolic Einstein (AHE in short) manifolds 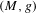 $(M,g)$ when the conformal boundary
$(M,g)$ when the conformal boundary 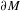 $\unicode[STIX]{x2202}M$ has dimension
$\unicode[STIX]{x2202}M$ has dimension  $n$ even. Its definition depends on the choice of metric
$n$ even. Its definition depends on the choice of metric 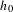 $h_{0}$ on
$h_{0}$ on 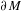 $\unicode[STIX]{x2202}M$ in the conformal class at infinity determined by
$\unicode[STIX]{x2202}M$ in the conformal class at infinity determined by  $g$, we denote it by
$g$, we denote it by 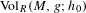 $\text{Vol}_{R}(M,g;h_{0})$. We show that
$\text{Vol}_{R}(M,g;h_{0})$. We show that 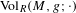 $\text{Vol}_{R}(M,g;\cdot )$ is a functional admitting a ‘Polyakov type’ formula in the conformal class
$\text{Vol}_{R}(M,g;\cdot )$ is a functional admitting a ‘Polyakov type’ formula in the conformal class 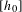 $[h_{0}]$ and we describe the critical points as solutions of some non-linear equation
$[h_{0}]$ and we describe the critical points as solutions of some non-linear equation 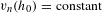 $v_{n}(h_{0})=\text{constant}$, satisfied in particular by Einstein metrics. When
$v_{n}(h_{0})=\text{constant}$, satisfied in particular by Einstein metrics. When 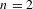 $n=2$, choosing extremizers in the conformal class amounts to uniformizing the surface, while if
$n=2$, choosing extremizers in the conformal class amounts to uniformizing the surface, while if 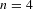 $n=4$ this amounts to solving the
$n=4$ this amounts to solving the 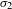 $\unicode[STIX]{x1D70E}_{2}$-Yamabe problem. Next, we consider the variation of
$\unicode[STIX]{x1D70E}_{2}$-Yamabe problem. Next, we consider the variation of 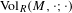 $\text{Vol}_{R}(M,\cdot ;\cdot )$ along a curve of AHE metrics
$\text{Vol}_{R}(M,\cdot ;\cdot )$ along a curve of AHE metrics 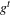 $g^{t}$ with boundary metric
$g^{t}$ with boundary metric 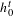 $h_{0}^{t}$ and we use this to show that, provided conformal classes can be (locally) parametrized by metrics
$h_{0}^{t}$ and we use this to show that, provided conformal classes can be (locally) parametrized by metrics 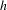 $h$ solving
$h$ solving 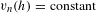 $v_{n}(h)=\text{constant}$ and
$v_{n}(h)=\text{constant}$ and 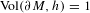 $\text{Vol}(\unicode[STIX]{x2202}M,h)=1$, the set of ends of AHE manifolds (up to diffeomorphisms isotopic to the identity) can be viewed as a Lagrangian submanifold in the cotangent space to the space
$\text{Vol}(\unicode[STIX]{x2202}M,h)=1$, the set of ends of AHE manifolds (up to diffeomorphisms isotopic to the identity) can be viewed as a Lagrangian submanifold in the cotangent space to the space 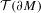 ${\mathcal{T}}(\unicode[STIX]{x2202}M)$ of conformal structures on
${\mathcal{T}}(\unicode[STIX]{x2202}M)$ of conformal structures on 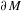 $\unicode[STIX]{x2202}M$. We obtain, as a consequence, a higher-dimensional version of McMullen’s quasi-Fuchsian reciprocity. We finally show that conformal classes admitting negatively curved Einstein metrics are local minima for the renormalized volume for a warped product type filling.
$\unicode[STIX]{x2202}M$. We obtain, as a consequence, a higher-dimensional version of McMullen’s quasi-Fuchsian reciprocity. We finally show that conformal classes admitting negatively curved Einstein metrics are local minima for the renormalized volume for a warped product type filling.
Keywords
MSC classification
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 17 , Issue 4 , September 2018 , pp. 853 - 912
- Copyright
- © Cambridge University Press 2016
Footnotes
C. G. was partially supported by the A.N.R. project ACG ANR-10-BLAN-0105. S. M. was partially supported by the CNCS project PN-II-RU-TE-2011-3-0053; he thanks the Fondation des Sciences Mathématiques de Paris and the École Normale Supérieure for additional support. J.-M. S. was partially supported by the A.N.R. through projects ETTT, ANR-09-BLAN-0116-01, and ACG, ANR-10-BLAN-0105.
References
- 2
- Cited by


