Article contents
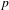 $p$-ADIC
$p$-ADIC  $L$-FUNCTIONS FOR ORDINARY FAMILIES ON SYMPLECTIC GROUPS
$L$-FUNCTIONS FOR ORDINARY FAMILIES ON SYMPLECTIC GROUPS
Published online by Cambridge University Press: 14 January 2019
Abstract
We construct the 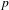 $p$-adic standard
$p$-adic standard  $L$-functions for ordinary families of Hecke eigensystems of the symplectic group
$L$-functions for ordinary families of Hecke eigensystems of the symplectic group 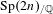 $\operatorname{Sp}(2n)_{/\mathbb{Q}}$ using the doubling method. We explain a clear and simple strategy of choosing the local sections for the Siegel Eisenstein series on the doubling group
$\operatorname{Sp}(2n)_{/\mathbb{Q}}$ using the doubling method. We explain a clear and simple strategy of choosing the local sections for the Siegel Eisenstein series on the doubling group 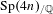 $\operatorname{Sp}(4n)_{/\mathbb{Q}}$, which guarantees the nonvanishing of local zeta integrals and allows us to
$\operatorname{Sp}(4n)_{/\mathbb{Q}}$, which guarantees the nonvanishing of local zeta integrals and allows us to 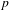 $p$-adically interpolate the restrictions of the Siegel Eisenstein series to
$p$-adically interpolate the restrictions of the Siegel Eisenstein series to 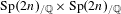 $\operatorname{Sp}(2n)_{/\mathbb{Q}}\times \operatorname{Sp}(2n)_{/\mathbb{Q}}$.
$\operatorname{Sp}(2n)_{/\mathbb{Q}}\times \operatorname{Sp}(2n)_{/\mathbb{Q}}$.
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 4 , July 2020 , pp. 1287 - 1347
- Copyright
- © Cambridge University Press 2019
References
- 9
- Cited by



