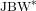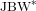Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Huang, Xujian
and
Tan, Dongni
2019.
A Tingley’s type problem in n-normed spaces.
Aequationes mathematicae,
Vol. 93,
Issue. 5,
p.
905.
Cueto-Avellaneda, María
and
Peralta, Antonio M.
2020.
Metric Characterisation of Unitaries in $$\hbox {JB}^*$$-Algebras.
Mediterranean Journal of Mathematics,
Vol. 17,
Issue. 4,
Kalenda, Ondřej F. K.
and
Peralta, Antonio M.
2021.
Extension of isometries from the unit sphere of a rank-2 Cartan factor.
Analysis and Mathematical Physics,
Vol. 11,
Issue. 1,
Tan, Dongni
and
Zhao, Kexin
2021.
A Property in Vector-Valued Function Spaces.
Results in Mathematics,
Vol. 76,
Issue. 1,
Cueto-Avellaneda, María
and
Peralta, Antonio M.
2022.
Can one identify two unital JB*-algebras by the metric spaces determined by their sets of unitaries?.
Linear and Multilinear Algebra,
Vol. 70,
Issue. 22,
p.
7702.
Cabezas, David
Cueto-Avellaneda, María
Hirota, Daisuke
Miura, Takeshi
and
Peralta, Antonio M.
2022.
Every commutative JB$$^*$$-triple satisfies the complex Mazur–Ulam property.
Annals of Functional Analysis,
Vol. 13,
Issue. 4,
Moslehian, M. S.
Muñoz-Fernández, G. A.
Peralta, A. M.
and
Seoane-Sepúlveda, J. B.
2022.
Similarities and differences between real and complex Banach spaces: an overview and recent developments.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 116,
Issue. 2,
Peralta, Antonio
2022.
On the extension of surjective isometries whose domain is the unit sphere of a space of compact operators.
Filomat,
Vol. 36,
Issue. 9,
p.
3075.
Jung, Soon-Mo
2022.
Extension of isometries in real Hilbert spaces.
Open Mathematics,
Vol. 20,
Issue. 1,
p.
1353.
Cueto-Avellaneda, María
Enami, Yuta
Hirota, Daisuke
Miura, Takeshi
and
Peralta, Antonio M.
2022.
Surjective isometries between unitary sets of unital JB⁎-algebras.
Linear Algebra and its Applications,
Vol. 643,
Issue. ,
p.
39.
Cueto-Avellaneda, María
Hirota, Daisuke
Miura, Takeshi
and
Peralta, Antonio M.
2023.
Exploring new solutions to Tingley’s problem for function algebras.
Quaestiones Mathematicae,
Vol. 46,
Issue. 7,
p.
1315.