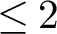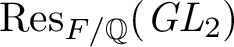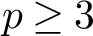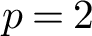1 Introduction
Let p be a rational prime and let N be a positive integer which is prime to p. We fix an algebraic closure
![]() $\bar {\mathbb {Q}}_{p}$
of
$\bar {\mathbb {Q}}_{p}$
of
![]() $\mathbb {Q}_{p}$
and denote its p-adic completion by
$\mathbb {Q}_{p}$
and denote its p-adic completion by
![]() $\mathbb {C}_{p}$
. Let
$\mathbb {C}_{p}$
. Let
![]() $\mathcal {W}_{\mathbb {Q}}$
be the weight space for
$\mathcal {W}_{\mathbb {Q}}$
be the weight space for
![]() $GL_{2,\mathbb {Q}}$
, which is a rigid analytic variety over
$GL_{2,\mathbb {Q}}$
, which is a rigid analytic variety over
![]() $\mathbb {Q}_{p}$
such that the set of
$\mathbb {Q}_{p}$
such that the set of
![]() $ \mathbb {C}_{p}$
-valued points
$ \mathbb {C}_{p}$
-valued points
![]() $\mathcal {W}_{\mathbb {Q}}\left (\mathbb {C}_{p}\right )$
is identified with the set of continuous homomorphisms
$\mathcal {W}_{\mathbb {Q}}\left (\mathbb {C}_{p}\right )$
is identified with the set of continuous homomorphisms
![]() $\mathbb {Z}_{p}^{\times }\to \mathbb {C}_{p}^{\times }$
.
$\mathbb {Z}_{p}^{\times }\to \mathbb {C}_{p}^{\times }$
.
In [Reference Coleman and Mazur15, Reference Buzzard12], Coleman and Mazur and Buzzard defined a rigid analytic curve
![]() $\mathcal {C}_{N}$
with a morphism
$\mathcal {C}_{N}$
with a morphism
![]() $\kappa : \mathcal {C}_{N}\to \mathcal {W}_{\mathbb {Q}}$
such that the set of
$\kappa : \mathcal {C}_{N}\to \mathcal {W}_{\mathbb {Q}}$
such that the set of
![]() $\mathbb {C}_{p}$
-valued points
$\mathbb {C}_{p}$
-valued points
![]() $\mathcal {C}_{N}\left (\mathbb {C}_{p}\right )$
is in bijection with the set of normalized overconvergent elliptic eigenforms of tame level N which are of finite slopes, in such a way that the eigenform f corresponding to a point
$\mathcal {C}_{N}\left (\mathbb {C}_{p}\right )$
is in bijection with the set of normalized overconvergent elliptic eigenforms of tame level N which are of finite slopes, in such a way that the eigenform f corresponding to a point
![]() $x\in \mathcal {C}_{N}\left (\mathbb {C}_{p}\right )$
is of weight
$x\in \mathcal {C}_{N}\left (\mathbb {C}_{p}\right )$
is of weight
![]() $\kappa (x)$
. The curve
$\kappa (x)$
. The curve
![]() $\mathcal {C}_{N}$
is called the Coleman–Mazur eigencurve, and it has played an important role in arithmetic geometry, since it turned out to be useful to control p-adic congruences of elliptic modular forms. After their construction of the eigencurve, much progress has been made to generalize it to the case of automorphic forms on algebraic groups other than
$\mathcal {C}_{N}$
is called the Coleman–Mazur eigencurve, and it has played an important role in arithmetic geometry, since it turned out to be useful to control p-adic congruences of elliptic modular forms. After their construction of the eigencurve, much progress has been made to generalize it to the case of automorphic forms on algebraic groups other than
![]() $GL_{2,\mathbb {Q}}$
. Now we have, for various algebraic groups G over a number field, a similar rigid analytic variety
$GL_{2,\mathbb {Q}}$
. Now we have, for various algebraic groups G over a number field, a similar rigid analytic variety
![]() $\mathcal {E}$
to the Coleman–Mazur eigencurve over a weight space
$\mathcal {E}$
to the Coleman–Mazur eigencurve over a weight space
![]() $\mathcal {W}^{G}$
for G, which is called the eigenvariety for G.
$\mathcal {W}^{G}$
for G, which is called the eigenvariety for G.
Despite their importance, we still do not know much about the geometry of eigenvarieties. For example, we do not even know if an eigenvariety has finitely many irreducible components. One of the topics of active research is the smoothness of eigenvarieties at classical points. For the Coleman–Mazur eigencurve, we know the smoothness at classical points in many cases [Reference Bellaïche and Chenevier6, Reference Bellaïche and Dimitrov8, Reference Hida30, Reference Kisin32]. Bellaïche and Chenevier [Reference Bellaïche and Chenevier7] studied tangent spaces of their eigenvariety for unitary groups at certain classical points, and applied it to showing the nonvanishing of a Bloch–Kato Selmer group. On the other hand, Bellaïche proved the nonsmoothness of the eigenvariety for
![]() $U(3)$
at classical points [Reference Bellaïche5]. It is natural to think that such geometric information of eigenvarieties is related to deep p-adic properties of automorphic forms.
$U(3)$
at classical points [Reference Bellaïche5]. It is natural to think that such geometric information of eigenvarieties is related to deep p-adic properties of automorphic forms.
Another interesting topic, which this paper is concerned with, is the properness of eigenvarieties over weight spaces. Since eigenvarieties are not of finite type over weight spaces, they are not proper in the usual sense. Instead, we consider the following geometric interpretation of the nonexistence of holes: Let
![]() $ \mathcal {D}_{\mathbb {C}_{p}}=\mathrm {Sp}\left (\mathbb {C}_{p}\langle T \rangle \right )$
be the closed unit disc centered at the origin O and let
$ \mathcal {D}_{\mathbb {C}_{p}}=\mathrm {Sp}\left (\mathbb {C}_{p}\langle T \rangle \right )$
be the closed unit disc centered at the origin O and let
 $\mathcal {D}^{\times }_{\mathbb {C}_{p}}=\mathcal {D}_{\mathbb {C}_{p}}\setminus \{O\}$
be the punctured disc. For any quasi-separated rigid analytic variety
$\mathcal {D}^{\times }_{\mathbb {C}_{p}}=\mathcal {D}_{\mathbb {C}_{p}}\setminus \{O\}$
be the punctured disc. For any quasi-separated rigid analytic variety
![]() $\mathcal {X}$
, we write
$\mathcal {X}$
, we write
![]() $\mathcal {X}_{\mathbb {C}_{p}}$
for the base extension of
$\mathcal {X}_{\mathbb {C}_{p}}$
for the base extension of
![]() $\mathcal {X}$
to
$\mathcal {X}$
to
![]() $\mathrm {Sp}\left (\mathbb {C}_{p}\right )$
. Suppose that we have a commutative diagram of rigid analytic varieties
$\mathrm {Sp}\left (\mathbb {C}_{p}\right )$
. Suppose that we have a commutative diagram of rigid analytic varieties

where the vertical arrows are the natural maps. Then we say that the eigenvariety
![]() $\mathcal {E}$
is proper if there exists a morphism
$\mathcal {E}$
is proper if there exists a morphism
![]() $\mathcal {D}_{\mathbb {C}_{p}}\to \mathcal {E}_{\mathbb {C}_{p}}$
such that the diagram is still commutative with this morphism added. Roughly speaking, this means that any family of overconvergent eigenforms of finite slopes on G parametrized by the punctured disc can always be extended to the puncture. However, note that what eigenvarieties parametrize are in general not eigenforms themselves but eigensystems occurring in the space of overconvergent automorphic forms. We also note that the naive interpretation of the nonexistence of holes – that any p-adically convergent sequence of overconvergent eigenforms of finite slopes converges to an overconvergent eigenform of finite slope – is false [Reference Coleman and Stein16, Theorem 2.1].
$\mathcal {D}_{\mathbb {C}_{p}}\to \mathcal {E}_{\mathbb {C}_{p}}$
such that the diagram is still commutative with this morphism added. Roughly speaking, this means that any family of overconvergent eigenforms of finite slopes on G parametrized by the punctured disc can always be extended to the puncture. However, note that what eigenvarieties parametrize are in general not eigenforms themselves but eigensystems occurring in the space of overconvergent automorphic forms. We also note that the naive interpretation of the nonexistence of holes – that any p-adically convergent sequence of overconvergent eigenforms of finite slopes converges to an overconvergent eigenform of finite slope – is false [Reference Coleman and Stein16, Theorem 2.1].
For the properness of the Coleman–Mazur eigencurve
![]() $\mathcal {C}_{N}$
, Buzzard and Calegari first proved the properness of
$\mathcal {C}_{N}$
, Buzzard and Calegari first proved the properness of
![]() $\mathcal {C}_{N}$
for the case where
$\mathcal {C}_{N}$
for the case where
![]() $p=2$
and
$p=2$
and
![]() $N=1$
[Reference Buzzard and Calegari13]. It was followed by Calegari’s result [Reference Calegari14] on the properness of
$N=1$
[Reference Buzzard and Calegari13]. It was followed by Calegari’s result [Reference Calegari14] on the properness of
![]() $\mathcal {C}_{N}$
at integral weights: he showed the existence of the map
$\mathcal {C}_{N}$
at integral weights: he showed the existence of the map
![]() $\mathcal {D}_{\mathbb {C}_{p}}\to \mathcal {C}_{N,{\mathbb {C}_{p}}}$
as in the definition of properness if the image of the puncture O in the weight space corresponds to a classical weight. One of the key points of their proofs is to show that any nonzero overconvergent elliptic eigenform of infinite slope does not converge on a certain region of a modular curve, while any overconvergent elliptic eigenform of finite slope does converge on a larger region. In [Reference Buzzard and Calegari13], they deduced the former from the theory of canonical subgroups, especially a behavior of the
$\mathcal {D}_{\mathbb {C}_{p}}\to \mathcal {C}_{N,{\mathbb {C}_{p}}}$
as in the definition of properness if the image of the puncture O in the weight space corresponds to a classical weight. One of the key points of their proofs is to show that any nonzero overconvergent elliptic eigenform of infinite slope does not converge on a certain region of a modular curve, while any overconvergent elliptic eigenform of finite slope does converge on a larger region. In [Reference Buzzard and Calegari13], they deduced the former from the theory of canonical subgroups, especially a behavior of the
![]() $U_{p}$
-correspondence for elliptic curves with Hodge height
$U_{p}$
-correspondence for elliptic curves with Hodge height
![]() $p/(p+1)$
, and the latter is a consequence of a standard analytic continuation argument via the
$p/(p+1)$
, and the latter is a consequence of a standard analytic continuation argument via the
![]() $U_{p}$
-operator. Recently, the properness of the Coleman–Mazur eigencurve was proved in full generality by Diao and Liu [Reference Diao and Liu22] using p-adic Hodge theory, especially the theory of trianguline p-adic representations in families.
$U_{p}$
-operator. Recently, the properness of the Coleman–Mazur eigencurve was proved in full generality by Diao and Liu [Reference Diao and Liu22] using p-adic Hodge theory, especially the theory of trianguline p-adic representations in families.
For algebraic groups other than
![]() $GL_{2,\mathbb {Q}}$
, the properness of eigenvarieties has not been known. Note that in Diao and Liu’s proof of the properness of the Coleman–Mazur eigencurve, in order to apply p-adic Hodge theory it seems crucial that we have a Galois representation, not just a Galois pseudorepresentation, over (the normalization of) the eigencurve. This is a consequence of the fact that we can convert pseudorepresentations into representations over smooth rigid analytic curves [Reference Coleman and Mazur15, remark after Theorem 5.1.2]. Thus, at present, it is unclear if their proof can be generalized to show the properness of eigenvarieties of dimension greater than
$GL_{2,\mathbb {Q}}$
, the properness of eigenvarieties has not been known. Note that in Diao and Liu’s proof of the properness of the Coleman–Mazur eigencurve, in order to apply p-adic Hodge theory it seems crucial that we have a Galois representation, not just a Galois pseudorepresentation, over (the normalization of) the eigencurve. This is a consequence of the fact that we can convert pseudorepresentations into representations over smooth rigid analytic curves [Reference Coleman and Mazur15, remark after Theorem 5.1.2]. Thus, at present, it is unclear if their proof can be generalized to show the properness of eigenvarieties of dimension greater than
![]() $1$
on the components where the residual Galois representations attached to automorphic forms are absolutely reducible.
$1$
on the components where the residual Galois representations attached to automorphic forms are absolutely reducible.
The aim of this paper is to generalize the method of Buzzard and Calegari to the case of Hilbert modular forms and to obtain the properness of the Hilbert eigenvariety constructed by Andreatta, Iovita, and Pilloni [Reference Andreatta, Iovita and Pilloni4] at integral weights in some cases.
To state the main theorem, we fix some notation. For any totally real number field F with ring of integers
![]() $\mathcal {O}_{F}$
, put
$\mathcal {O}_{F}$
, put
![]() $G=\mathrm {Res}_{F/\mathbb {Q}}(\mathit {GL}_{2})$
and
$G=\mathrm {Res}_{F/\mathbb {Q}}(\mathit {GL}_{2})$
and
![]() $\mathbb {T}=\mathrm {Res}_{\mathcal {O}_{F}/\mathbb {Z}}(\mathbb {G}_{\mathrm {m}})$
. Let
$\mathbb {T}=\mathrm {Res}_{\mathcal {O}_{F}/\mathbb {Z}}(\mathbb {G}_{\mathrm {m}})$
. Let
![]() $K/\mathbb {Q}_{p}$
be a finite extension such that
$K/\mathbb {Q}_{p}$
be a finite extension such that
![]() $F\otimes K$
splits completely. Let
$F\otimes K$
splits completely. Let
![]() $\mathcal {W}^{G}$
be the weight space for G over K as in [Reference Andreatta, Iovita and Pilloni4, §4.1]. By definition, we have
$\mathcal {W}^{G}$
be the weight space for G over K as in [Reference Andreatta, Iovita and Pilloni4, §4.1]. By definition, we have
 $$ \begin{align*} \mathcal{W}^{G}=\mathrm{Spf}\left(\mathcal{O}_{K}\left[\left[\mathbb{T}\left(\mathbb{Z}_{p}\right)\times \mathbb{Z}_{p}^{\times}\right]\right]\right)^{\mathrm{rig}}, \end{align*} $$
$$ \begin{align*} \mathcal{W}^{G}=\mathrm{Spf}\left(\mathcal{O}_{K}\left[\left[\mathbb{T}\left(\mathbb{Z}_{p}\right)\times \mathbb{Z}_{p}^{\times}\right]\right]\right)^{\mathrm{rig}}, \end{align*} $$
and the set of
![]() $\mathbb {C}_{p}$
-valued points
$\mathbb {C}_{p}$
-valued points
![]() $\mathcal {W}^{G}\left (\mathbb {C}_{p}\right )$
can be identified with the set of pairs of continuous characters
$\mathcal {W}^{G}\left (\mathbb {C}_{p}\right )$
can be identified with the set of pairs of continuous characters
We say that the weight
![]() $(\nu ,w)$
is
$(\nu ,w)$
is
![]() $1$
-integral if its restriction to
$1$
-integral if its restriction to
![]() $1+p\left (\mathcal {O}_{F}\otimes \mathbb {Z}_{p}\right )\times \left (1+p\mathbb {Z}_{p}\right )$
comes from an algebraic character
$1+p\left (\mathcal {O}_{F}\otimes \mathbb {Z}_{p}\right )\times \left (1+p\mathbb {Z}_{p}\right )$
comes from an algebraic character
![]() $\mathbb {T}\times \mathbb {G}_{\mathrm {m}} \to \mathbb {G}_{\mathrm {m}}$
. This restriction corresponds to a pair
$\mathbb {T}\times \mathbb {G}_{\mathrm {m}} \to \mathbb {G}_{\mathrm {m}}$
. This restriction corresponds to a pair
 $\left (\left (k_{\beta }\right )_{\beta },k_{0}\right )$
of a tuple
$\left (\left (k_{\beta }\right )_{\beta },k_{0}\right )$
of a tuple
 $\left (k_{\beta }\right )_{\beta }$
of integers indexed by the set of embeddings
$\left (k_{\beta }\right )_{\beta }$
of integers indexed by the set of embeddings
![]() $\beta : F\to K$
and an integer
$\beta : F\to K$
and an integer
![]() $k_{0}$
. We say that a
$k_{0}$
. We say that a
![]() $1$
-integral weight is
$1$
-integral weight is
![]() $1$
-doubly even if every
$1$
-doubly even if every
![]() $k_{\beta }$
and
$k_{\beta }$
and
![]() $k_{0}$
are divisible by
$k_{0}$
are divisible by
![]() $4$
. Then the main theorem in this paper is the following:
$4$
. Then the main theorem in this paper is the following:
Theorem 1.1 (Theorem 5.1)
Let F be a totally real number field which is unramified over p. Let
![]() $K/\mathbb {Q}_{p}$
be a finite extension in
$K/\mathbb {Q}_{p}$
be a finite extension in
![]() $\bar {\mathbb {Q}}_{p}$
such that
$\bar {\mathbb {Q}}_{p}$
such that
![]() $F\otimes K$
splits completely. Let
$F\otimes K$
splits completely. Let
![]() $N\geq 4$
be an integer prime to p. Let
$N\geq 4$
be an integer prime to p. Let
![]() $\mathcal {E}\to \mathcal {W}^{G}$
be the Hilbert eigenvariety of tame level N constructed in [Reference Andreatta, Iovita and Pilloni4, §5], which is defined over a finite extension of K.
$\mathcal {E}\to \mathcal {W}^{G}$
be the Hilbert eigenvariety of tame level N constructed in [Reference Andreatta, Iovita and Pilloni4, §5], which is defined over a finite extension of K.
Suppose that for any prime ideal
![]() $\mathfrak {p}$
of F dividing p, the residue degree
$\mathfrak {p}$
of F dividing p, the residue degree
![]() $f_{\mathfrak {p}}$
of
$f_{\mathfrak {p}}$
of
![]() $\mathfrak {p}$
satisfies
$\mathfrak {p}$
satisfies
![]() $f_{\mathfrak {p}}\leq 2$
(resp., p splits completely in F) if p is odd (resp., even). Then
$f_{\mathfrak {p}}\leq 2$
(resp., p splits completely in F) if p is odd (resp., even). Then
![]() $\mathcal {E}$
is proper at
$\mathcal {E}$
is proper at
![]() $1$
-integral (resp.,
$1$
-integral (resp.,
![]() $1$
-doubly even) weights. Namely, any commutative diagram of rigid analytic varieties over
$1$
-doubly even) weights. Namely, any commutative diagram of rigid analytic varieties over
![]() $\mathbb {C}_{p}$
$\mathbb {C}_{p}$

can be filled with the dotted arrow if
![]() $\psi (O)$
corresponds to a
$\psi (O)$
corresponds to a
![]() $1$
-integral (resp.,
$1$
-integral (resp.,
![]() $1$
-doubly even) weight.
$1$
-doubly even) weight.
For the proof, we basically follow the idea of Buzzard and Calegari [Reference Buzzard and Calegari13, Reference Calegari14]. Thus the key step in our case is also to show that any nonzero overconvergent Hilbert eigenform f of
![]() $1$
-integral weight and infinite slope does not converge on the locus where all the partial Hodge heights are no more than
$1$
-integral weight and infinite slope does not converge on the locus where all the partial Hodge heights are no more than
![]() $1/(p+1)$
in a Hilbert modular variety.
$1/(p+1)$
in a Hilbert modular variety.
Let us explain briefly how to show this nonconvergence property, following [Reference Buzzard and Calegari13]. For simplicity, we assume that f is of integral weight, namely the weight
![]() $(\nu ,w)$
corresponds to an algebraic character
$(\nu ,w)$
corresponds to an algebraic character
![]() $\mathbb {T}\times \mathbb {G}_{\mathrm {m}}\to \mathbb {G}_{\mathrm {m}}$
. For any Hilbert–Blumenthal abelian variety (HBAV) A with an
$\mathbb {T}\times \mathbb {G}_{\mathrm {m}}\to \mathbb {G}_{\mathrm {m}}$
. For any Hilbert–Blumenthal abelian variety (HBAV) A with an
![]() $\mathcal {O}_{F}$
-action over the ring of integers
$\mathcal {O}_{F}$
-action over the ring of integers
![]() $\mathcal {O}_{L}$
of a finite extension
$\mathcal {O}_{L}$
of a finite extension
![]() $L/K$
, we say that a finite flat closed
$L/K$
, we say that a finite flat closed
![]() $\mathcal {O}_{F}$
-subgroup scheme
$\mathcal {O}_{F}$
-subgroup scheme
![]() $\mathcal {H}$
of A over
$\mathcal {H}$
of A over
![]() $\mathcal {O}_{L}$
is p-cyclic if its generic fiber is étale locally isomorphic to the constant group scheme
$\mathcal {O}_{L}$
is p-cyclic if its generic fiber is étale locally isomorphic to the constant group scheme
![]() $\underline {\mathcal {O}_{F}/p\mathcal {O}_{F}}$
. We say that A is critical if every
$\underline {\mathcal {O}_{F}/p\mathcal {O}_{F}}$
. We say that A is critical if every
![]() $\beta $
-Hodge height of A is equal to
$\beta $
-Hodge height of A is equal to
![]() $p/(p+1)$
for any embedding
$p/(p+1)$
for any embedding
![]() $\beta : F\to K$
. Then, for any critical A and any p-cyclic subgroup scheme
$\beta : F\to K$
. Then, for any critical A and any p-cyclic subgroup scheme
![]() $\mathcal {H}$
of A, the quotient
$\mathcal {H}$
of A, the quotient
![]() $A/\mathcal {H}$
has the canonical subgroup
$A/\mathcal {H}$
has the canonical subgroup
![]() $A[p]/\mathcal {H}$
of level
$A[p]/\mathcal {H}$
of level
![]() $1$
and its
$1$
and its
![]() $\beta $
-Hodge heights are all
$\beta $
-Hodge heights are all
![]() $1/(p+1)$
[Reference Hattori29, Proposition 6.1]. This is where the assumption on residue degrees is used in the most crucial way. It is unclear if the claim holds without this assumption: at least, we have a counterexample of a similar assertion for truncated Barsotti–Tate groups if we drop the assumption on
$1/(p+1)$
[Reference Hattori29, Proposition 6.1]. This is where the assumption on residue degrees is used in the most crucial way. It is unclear if the claim holds without this assumption: at least, we have a counterexample of a similar assertion for truncated Barsotti–Tate groups if we drop the assumption on
![]() $f_{\mathfrak {p}}$
[Reference Hattori29, Remark 6.2].
$f_{\mathfrak {p}}$
[Reference Hattori29, Remark 6.2].
Consider the Hilbert modular variety classifying pairs
![]() $(A,\mathcal {H})$
of an HBAV A and its p-cyclic subgroup scheme
$(A,\mathcal {H})$
of an HBAV A and its p-cyclic subgroup scheme
![]() $\mathcal {H}$
. Let
$\mathcal {H}$
. Let
![]() $\mathcal {U}$
be the locus where
$\mathcal {U}$
be the locus where
![]() $\mathcal {H}$
is the canonical subgroup of A. Another thing we need here is to show that for any
$\mathcal {H}$
is the canonical subgroup of A. Another thing we need here is to show that for any
![]() $(A,\mathcal {H})$
with A critical, the corresponding point
$(A,\mathcal {H})$
with A critical, the corresponding point
![]() $[(A,\mathcal {H})]$
of the Hilbert modular variety has a connected admissible affinoid open neighborhood intersecting
$[(A,\mathcal {H})]$
of the Hilbert modular variety has a connected admissible affinoid open neighborhood intersecting
![]() $\mathcal {U}$
such that, if an overconvergent Hilbert eigenform f of integral weight converges on the locus where all the
$\mathcal {U}$
such that, if an overconvergent Hilbert eigenform f of integral weight converges on the locus where all the
![]() $\beta $
-Hodge heights are
$\beta $
-Hodge heights are
![]() $\leq 1/(p+1)$
, then we can evaluate
$\leq 1/(p+1)$
, then we can evaluate
![]() $U_{p}f$
on this neighborhood (Proposition 3.7). This implies that if f is in addition of infinite slope, then we have
$U_{p}f$
on this neighborhood (Proposition 3.7). This implies that if f is in addition of infinite slope, then we have
![]() $\left (U_{p}f\right )(A,\mathcal {H})=0$
for any critical A and any p-cyclic subgroup scheme
$\left (U_{p}f\right )(A,\mathcal {H})=0$
for any critical A and any p-cyclic subgroup scheme
![]() $\mathcal {H}$
. From this, by a combinatorial argument (Lemma 5.2), we obtain
$\mathcal {H}$
. From this, by a combinatorial argument (Lemma 5.2), we obtain
![]() $f(A/\mathcal {H},A[p]/\mathcal {H})=0$
for any such
$f(A/\mathcal {H},A[p]/\mathcal {H})=0$
for any such
![]() $(A,\mathcal {H})$
, which yields
$(A,\mathcal {H})$
, which yields
![]() $f=0$
, and the nonconvergence property follows. It seems that this argument using a connected neighborhood cannot be generalized immediately to the case where f is not of locally algebraic weight, since in this case
$f=0$
, and the nonconvergence property follows. It seems that this argument using a connected neighborhood cannot be generalized immediately to the case where f is not of locally algebraic weight, since in this case
![]() $U_{p} f$
is defined only on the locus
$U_{p} f$
is defined only on the locus
![]() $\mathcal {U}$
(even after taking a finite étale cover) and it cannot be evaluated for any critical A.
$\mathcal {U}$
(even after taking a finite étale cover) and it cannot be evaluated for any critical A.
Note that sheaves of overconvergent Hilbert modular forms of [Reference Andreatta, Iovita and Pilloni4] are defined on the locus in the Hilbert modular variety where canonical subgroups exist. However, the theory of canonical subgroups used in [Reference Andreatta, Iovita and Pilloni4] does not give the existence locus which is enough large to contain critical HBAVs unless p is sufficiently large. Instead, we use [Reference Hattori29, Theorem 8.1], which enables us to enlarge the locus where sheaves of overconvergent Hilbert modular forms are defined from the original locus given in [Reference Andreatta, Iovita and Pilloni4], and to include the case of
![]() $p<5$
in the main theorem.
$p<5$
in the main theorem.
What the Hilbert eigenvariety
![]() $\mathcal {E}$
of [Reference Andreatta, Iovita and Pilloni4] parametrizes are eigensystems in the space of overconvergent Hilbert modular forms. Thus, to follow the strategy of Buzzard and Calegari to reduce properness to the nonconvergence property of overconvergent modular forms, we have to convert a family of eigensystems of finite slopes, or a morphism from a rigid analytic variety to
$\mathcal {E}$
of [Reference Andreatta, Iovita and Pilloni4] parametrizes are eigensystems in the space of overconvergent Hilbert modular forms. Thus, to follow the strategy of Buzzard and Calegari to reduce properness to the nonconvergence property of overconvergent modular forms, we have to convert a family of eigensystems of finite slopes, or a morphism from a rigid analytic variety to
![]() $\mathcal {E}$
, into a family of eigenforms and vice versa. The latter direction can be treated (Proposition 2.7) as in the proof of [Reference Bellaïche and Chenevier7, Proposition 7.2.8]. For the former direction, we first prove that any family of eigensystems over any smooth rigid analytic variety over
$\mathcal {E}$
, into a family of eigenforms and vice versa. The latter direction can be treated (Proposition 2.7) as in the proof of [Reference Bellaïche and Chenevier7, Proposition 7.2.8]. For the former direction, we first prove that any family of eigensystems over any smooth rigid analytic variety over
![]() $\mathbb {C}_{p}$
can be lifted locally to a family of eigenforms (Proposition 2.5). This can be considered as a version of Deligne and Serre’s lifting lemma [Reference Deligne and Serre21, Lemme 6.11]. Then we glue the local eigenforms using a weak multiplicity one result, after we normalize the local eigenforms with respect to the first q-expansion coefficient (Proposition 4.15). This use of weak multiplicity one and normalization via a q-expansion coefficient hinders us from generalizing the main theorem to the case of
$\mathbb {C}_{p}$
can be lifted locally to a family of eigenforms (Proposition 2.5). This can be considered as a version of Deligne and Serre’s lifting lemma [Reference Deligne and Serre21, Lemme 6.11]. Then we glue the local eigenforms using a weak multiplicity one result, after we normalize the local eigenforms with respect to the first q-expansion coefficient (Proposition 4.15). This use of weak multiplicity one and normalization via a q-expansion coefficient hinders us from generalizing the main theorem to the case of
![]() $GSp_{2g}$
, where sheaves of overconvergent Siegel modular forms and the Siegel eigenvariety are constructed in a similar way [Reference Andreatta, Iovita and Pilloni3].
$GSp_{2g}$
, where sheaves of overconvergent Siegel modular forms and the Siegel eigenvariety are constructed in a similar way [Reference Andreatta, Iovita and Pilloni3].
Once we have a family of overconvergent Hilbert eigenforms f of finite slopes parametrized by
 $\mathcal {D}^{\times }_{\mathbb {C}_{p}}$
associated to the family of eigensystems
$\mathcal {D}^{\times }_{\mathbb {C}_{p}}$
associated to the family of eigensystems
 $\varphi :\mathcal {D}^{\times }_{\mathbb {C}_{p}} \to \mathcal {E}_{\mathbb {C}_{p}}$
, we extend its domain of definition in the Hilbert modular variety as large as possible by an analytic continuation using the
$\varphi :\mathcal {D}^{\times }_{\mathbb {C}_{p}} \to \mathcal {E}_{\mathbb {C}_{p}}$
, we extend its domain of definition in the Hilbert modular variety as large as possible by an analytic continuation using the
![]() $U_{p}$
-operator. Since the Hecke eigenvalues are of absolute values bounded by
$U_{p}$
-operator. Since the Hecke eigenvalues are of absolute values bounded by
![]() $1$
, we can show that q-expansion defines a rigid analytic function around a cusp parametrized by
$1$
, we can show that q-expansion defines a rigid analytic function around a cusp parametrized by
 $\mathcal {D}^{\times }_{\mathbb {C}_{p}}$
which is of absolute value bounded by
$\mathcal {D}^{\times }_{\mathbb {C}_{p}}$
which is of absolute value bounded by
![]() $1$
. Such a function automatically extends to the puncture, and a gluing shows that f also extends to the puncture (Proposition 4.19). Since we analytically continued f to a large region, the specialization
$1$
. Such a function automatically extends to the puncture, and a gluing shows that f also extends to the puncture (Proposition 4.19). Since we analytically continued f to a large region, the specialization
![]() $f(O)$
at the puncture is also defined over the same large region. Thus the nonconvergence property of eigenforms of infinite slope implies that
$f(O)$
at the puncture is also defined over the same large region. Thus the nonconvergence property of eigenforms of infinite slope implies that
![]() $f(O)$
is also of finite slope, which gives us an extended map
$f(O)$
is also of finite slope, which gives us an extended map
![]() $\mathcal {D}_{\mathbb {C}_{p}}\to \mathcal {E}_{\mathbb {C}_{p}}$
.
$\mathcal {D}_{\mathbb {C}_{p}}\to \mathcal {E}_{\mathbb {C}_{p}}$
.
The organization of this paper is as follows. In §2, we recall Buzzard’s eigenvariety machine [Reference Buzzard12], on which the construction of the Hilbert eigenvariety in [Reference Andreatta, Iovita and Pilloni4] relies, and we prove results to convert a family of eigensystems into local eigenforms and vice versa. In §3, we recall the definition of overconvergent Hilbert modular forms and the construction of the Hilbert eigenvariety, both due to Andreatta, Iovita, and Pilloni [Reference Andreatta, Iovita and Pilloni4], including generalizations of some of their results to the case over
![]() $\mathbb {C}_{p}$
. We also give a connected neighborhood of any critical point in a Hilbert modular variety, which is one of the key ingredients of the proof of Theorem 1.1. In §4, we prove properties of the q-expansion for overconvergent Hilbert modular forms. These are used to produce a global eigenform by gluing local eigenforms obtained from a family of eigensystems, and also to extend a family of overconvergent Hilbert eigenforms over the punctured unit disc to the puncture. Combining these results, we prove Theorem 1.1 in §5.
$\mathbb {C}_{p}$
. We also give a connected neighborhood of any critical point in a Hilbert modular variety, which is one of the key ingredients of the proof of Theorem 1.1. In §4, we prove properties of the q-expansion for overconvergent Hilbert modular forms. These are used to produce a global eigenform by gluing local eigenforms obtained from a family of eigensystems, and also to extend a family of overconvergent Hilbert eigenforms over the punctured unit disc to the puncture. Combining these results, we prove Theorem 1.1 in §5.
2 Lemmata on Buzzard’s eigenvariety
Let p be a rational prime and let K be a finite extension of
![]() $\mathbb {Q}_{p}$
in
$\mathbb {Q}_{p}$
in
![]() $\bar {\mathbb {Q}}_{p}$
. In this section, we establish two lemmata on Buzzard’s eigenvariety machine [Reference Buzzard12]. In the first lemma, we show that any family of Hecke eigensystems over a smooth rigid analytic variety over
$\bar {\mathbb {Q}}_{p}$
. In this section, we establish two lemmata on Buzzard’s eigenvariety machine [Reference Buzzard12]. In the first lemma, we show that any family of Hecke eigensystems over a smooth rigid analytic variety over
![]() $\mathbb {C}_{p}$
lifts locally to a family of eigenforms. The second one enables us to convert any family of Hecke eigensystems of finite slopes over a reduced rigid analytic variety into a morphism to the eigenvariety.
$\mathbb {C}_{p}$
lifts locally to a family of eigenforms. The second one enables us to convert any family of Hecke eigensystems of finite slopes over a reduced rigid analytic variety into a morphism to the eigenvariety.
2.1 Buzzard’s eigenvariety machine
First we briefly recall the construction of Buzzard’s eigenvariety. Let R be a reduced K-affinoid algebra. Let M be a Banach R-module satisfying the condition
![]() $(Pr)$
of [Reference Buzzard12, §2]. We write
$(Pr)$
of [Reference Buzzard12, §2]. We write
![]() $\mathrm {End}_{R}^{\mathrm {cont}}(M)$
for the R-algebra of continuous R-endomorphisms of M. Let
$\mathrm {End}_{R}^{\mathrm {cont}}(M)$
for the R-algebra of continuous R-endomorphisms of M. Let
![]() $\mathbf {T}$
be a commutative K-algebra endowed with a K-algebra homomorphism
$\mathbf {T}$
be a commutative K-algebra endowed with a K-algebra homomorphism
![]() $\mathbf {T}\to \mathrm {End}_{R}^{\mathrm {cont}}(M)$
. Let
$\mathbf {T}\to \mathrm {End}_{R}^{\mathrm {cont}}(M)$
. Let
![]() $\phi $
be an element of
$\phi $
be an element of
![]() $\mathbf {T}$
. Suppose that
$\mathbf {T}$
. Suppose that
![]() $\phi $
acts on M as a compact operator. We call such a quadruple
$\phi $
acts on M as a compact operator. We call such a quadruple
![]() $(R,M,\mathbf {T},\phi )$
an input datum for the eigenvariety machine over K.
$(R,M,\mathbf {T},\phi )$
an input datum for the eigenvariety machine over K.
For such M and
![]() $M^{\prime }$
, a continuous R-linear
$M^{\prime }$
, a continuous R-linear
![]() $\mathbf {T}$
-module homomorphism
$\mathbf {T}$
-module homomorphism
![]() $\alpha :M^{\prime }\to M$
is called a primitive link if there exists a compact R-linear
$\alpha :M^{\prime }\to M$
is called a primitive link if there exists a compact R-linear
![]() $\mathbf {T}$
-module homomorphism
$\mathbf {T}$
-module homomorphism
![]() $c: M\to M^{\prime }$
such that
$c: M\to M^{\prime }$
such that
![]() $\phi $
acts on M as
$\phi $
acts on M as
![]() $\alpha \circ c$
and it acts on
$\alpha \circ c$
and it acts on
![]() $M^{\prime }$
as
$M^{\prime }$
as
![]() $c\circ \alpha $
. A continuous R-linear
$c\circ \alpha $
. A continuous R-linear
![]() $\mathbf {T}$
-module homomorphism
$\mathbf {T}$
-module homomorphism
![]() $\alpha :M^{\prime }\to M$
is called a link if it is the composite of a finite number of primitive links.
$\alpha :M^{\prime }\to M$
is called a link if it is the composite of a finite number of primitive links.
Let
 $P(T)=1+\sum _{n\geq 1} c_{n} T^{n}$
be the characteristic power series of
$P(T)=1+\sum _{n\geq 1} c_{n} T^{n}$
be the characteristic power series of
![]() $\phi $
acting on M, which is an element of the ring
$\phi $
acting on M, which is an element of the ring
![]() $R\{\{T\}\}$
of entire functions over R. The spectral variety
$R\{\{T\}\}$
of entire functions over R. The spectral variety
![]() $Z_{\phi }$
for
$Z_{\phi }$
for
![]() $\phi $
is the closed analytic subvariety of
$\phi $
is the closed analytic subvariety of
![]() $\mathrm {Sp}(R)\times \mathbb {A}^{1}$
defined by
$\mathrm {Sp}(R)\times \mathbb {A}^{1}$
defined by
![]() $P(T)$
. We denote the projection
$P(T)$
. We denote the projection
![]() $Z_{\phi }\to \mathrm {Sp}(R)$
by f.
$Z_{\phi }\to \mathrm {Sp}(R)$
by f.
The eigenvariety
![]() $\mathcal {E}$
associated to
$\mathcal {E}$
associated to
![]() $(R,M,\mathbf {T},\phi )$
is the rigid analytic variety over
$(R,M,\mathbf {T},\phi )$
is the rigid analytic variety over
![]() $Z_{\phi }$
, defined as follows: let
$Z_{\phi }$
, defined as follows: let
![]() $\mathcal {C}$
be the set of admissible affinoid open subsets Y of
$\mathcal {C}$
be the set of admissible affinoid open subsets Y of
![]() $Z_{\phi }$
satisfying the condition that there exists an affinoid subdomain X of
$Z_{\phi }$
satisfying the condition that there exists an affinoid subdomain X of
![]() $\mathrm {Sp}(R)$
such that
$\mathrm {Sp}(R)$
such that
![]() $Y\subseteq f^{-1}(X)$
and the map
$Y\subseteq f^{-1}(X)$
and the map
![]() $Y\to X$
induced by f is finite and surjective. We can show that
$Y\to X$
induced by f is finite and surjective. We can show that
![]() $\mathcal {C}$
is an admissible covering of
$\mathcal {C}$
is an admissible covering of
![]() $Z_{\phi }$
[Reference Buzzard12, §4, Theorem], and we refer to
$Z_{\phi }$
[Reference Buzzard12, §4, Theorem], and we refer to
![]() $\mathcal {C}$
as the canonical admissible covering of
$\mathcal {C}$
as the canonical admissible covering of
![]() $Z_{\phi }$
.
$Z_{\phi }$
.
Let
![]() $Y=\mathrm {Sp}(B)$
be an element of
$Y=\mathrm {Sp}(B)$
be an element of
![]() $\mathcal {C}$
and let
$\mathcal {C}$
and let
![]() $X=\mathrm {Sp}(A)$
be as before. Suppose that X is connected. Then the A-algebra B is projective of constant rank d. In the ring of entire functions
$X=\mathrm {Sp}(A)$
be as before. Suppose that X is connected. Then the A-algebra B is projective of constant rank d. In the ring of entire functions
![]() $A\{\{T\}\}$
over A, we can show that
$A\{\{T\}\}$
over A, we can show that
![]() $P(T)$
can be written as
$P(T)$
can be written as
![]() $P(T)=Q(T)S(T)$
with some
$P(T)=Q(T)S(T)$
with some
![]() $S(T)\in A\{\{T\}\}$
and a polynomial
$S(T)\in A\{\{T\}\}$
and a polynomial
![]() $Q(T)$
of degree d over A with constant term
$Q(T)$
of degree d over A with constant term
![]() $1$
, and that we have a natural isomorphism
$1$
, and that we have a natural isomorphism
![]() $A[T]/(Q(T))\simeq B$
. Put
$A[T]/(Q(T))\simeq B$
. Put
 $Q^{*}(T)=T^{d} Q\left (T^{-1}\right )$
. By the Riesz theory [Reference Buzzard12, Theorem 3.3], the restriction
$Q^{*}(T)=T^{d} Q\left (T^{-1}\right )$
. By the Riesz theory [Reference Buzzard12, Theorem 3.3], the restriction
![]() $M_{A}$
of M to
$M_{A}$
of M to
![]() $X=\mathrm {Sp}(A)$
can be uniquely decomposed as
$X=\mathrm {Sp}(A)$
can be uniquely decomposed as
![]() $M_{A}=N\oplus F$
, where N is a projective A-module of rank d such that
$M_{A}=N\oplus F$
, where N is a projective A-module of rank d such that
![]() $Q^{*}(\phi )$
acts on N as the zero map and it acts on F as an isomorphism. Since
$Q^{*}(\phi )$
acts on N as the zero map and it acts on F as an isomorphism. Since
![]() $Q^{*}(0)\neq 0$
, the operator
$Q^{*}(0)\neq 0$
, the operator
![]() $\phi $
is invertible on N. Let
$\phi $
is invertible on N. Let
![]() $\mathbf {T}(Y)$
be the A-subalgebra of
$\mathbf {T}(Y)$
be the A-subalgebra of
![]() $\mathrm {End}_{A}^{\mathrm {cont}}(N)$
generated by the image of
$\mathrm {End}_{A}^{\mathrm {cont}}(N)$
generated by the image of
![]() $\mathbf {T}$
. Then the A-algebra
$\mathbf {T}$
. Then the A-algebra
![]() $ \mathbf {T}(Y)$
is finite and thus a K-affinoid algebra. Moreover, we have a natural A-algebra homomorphism
$ \mathbf {T}(Y)$
is finite and thus a K-affinoid algebra. Moreover, we have a natural A-algebra homomorphism
![]() $A[T]/(Q(T))\simeq B\to \mathbf {T}(Y)$
sending T to
$A[T]/(Q(T))\simeq B\to \mathbf {T}(Y)$
sending T to
![]() $(\phi \rvert _{N})^{-1}$
. Put
$(\phi \rvert _{N})^{-1}$
. Put
![]() $\mathcal {E}(Y)=\mathrm {Sp}(\mathbf {T}(Y))$
. If X is not connected, by decomposing X into connected components as
$\mathcal {E}(Y)=\mathrm {Sp}(\mathbf {T}(Y))$
. If X is not connected, by decomposing X into connected components as
![]() $X=\coprod _{i} X_{i}$
we put
$X=\coprod _{i} X_{i}$
we put
![]() $ \mathcal {E}(Y)=\coprod _{i} \mathcal {E}\left (Y\rvert _{X_{i}}\right )$
. Then these local pieces can be glued along the admissible covering
$ \mathcal {E}(Y)=\coprod _{i} \mathcal {E}\left (Y\rvert _{X_{i}}\right )$
. Then these local pieces can be glued along the admissible covering
![]() $\mathcal {C}$
and define the eigenvariety
$\mathcal {C}$
and define the eigenvariety
![]() $\mathcal {E}\to Z_{\phi }$
[Reference Buzzard12, §5]. By [Reference Buzzard12, Lemma 5.3], the rigid analytic varieties
$\mathcal {E}\to Z_{\phi }$
[Reference Buzzard12, §5]. By [Reference Buzzard12, Lemma 5.3], the rigid analytic varieties
![]() $\mathcal {E}$
and
$\mathcal {E}$
and
![]() $Z_{\phi }$
are separated.
$Z_{\phi }$
are separated.
By the construction, the natural map
![]() $\mathcal {E}\to Z_{\phi }$
is finite and the structure morphism
$\mathcal {E}\to Z_{\phi }$
is finite and the structure morphism
![]() $\mathcal {E}\to \mathrm {Sp}(R)$
is locally (with respect to both the source and the target) finite. Moreover, we have a K-algebra homomorphism
$\mathcal {E}\to \mathrm {Sp}(R)$
is locally (with respect to both the source and the target) finite. Moreover, we have a K-algebra homomorphism
![]() $\mathbf {T}\to \mathcal {O}(\mathcal {E})$
such that, for any admissible affinoid open subset V of
$\mathbf {T}\to \mathcal {O}(\mathcal {E})$
such that, for any admissible affinoid open subset V of
![]() $Z_{\phi }$
, the induced map
$Z_{\phi }$
, the induced map
![]() $\mathbf {T}\otimes _{K} \mathcal {O}(V)\to \mathcal {O}(\mathcal {E}\rvert _{V})$
is surjective.
$\mathbf {T}\otimes _{K} \mathcal {O}(V)\to \mathcal {O}(\mathcal {E}\rvert _{V})$
is surjective.
In some cases we can glue this construction to define the eigenvariety over a nonaffinoid base space. Let
![]() $\mathcal {W}$
be a reduced rigid analytic variety over K. Let
$\mathcal {W}$
be a reduced rigid analytic variety over K. Let
![]() $\mathbf {T}$
be a commutative K-algebra and let
$\mathbf {T}$
be a commutative K-algebra and let
![]() $\phi $
be an element of
$\phi $
be an element of
![]() $\mathbf {T}$
. Suppose that for any admissible affinoid open subset
$\mathbf {T}$
. Suppose that for any admissible affinoid open subset
![]() $X\subseteq \mathcal {W}$
, we are given a Banach
$X\subseteq \mathcal {W}$
, we are given a Banach
![]() $\mathcal {O}(X)$
-module
$\mathcal {O}(X)$
-module
![]() $M_{X}$
satisfying condition
$M_{X}$
satisfying condition
![]() $(Pr)$
with a K-algebra homomorphism
$(Pr)$
with a K-algebra homomorphism
 $\mathbf {T}\to \mathrm {End}_{\mathcal {O}(X)}^{\mathrm {cont}}(M_{X})$
such that the image of
$\mathbf {T}\to \mathrm {End}_{\mathcal {O}(X)}^{\mathrm {cont}}(M_{X})$
such that the image of
![]() $\phi $
is a compact operator. Suppose also that for any admissible affinoid open subsets
$\phi $
is a compact operator. Suppose also that for any admissible affinoid open subsets
![]() $X_{1}\subseteq X_{2}\subseteq \mathcal {W}$
, we have a continuous
$X_{1}\subseteq X_{2}\subseteq \mathcal {W}$
, we have a continuous
![]() $\mathcal {O}(X_{1})$
-module homomorphism
$\mathcal {O}(X_{1})$
-module homomorphism
 $\alpha : M_{X_{1}}\to M_{X_{2}}\hat {\otimes }_{\mathcal {O}\left (X_{2}\right )} \mathcal {O}(X_{1})$
, which is a link and satisfies a cocycle condition. Then the eigenvarieties for
$\alpha : M_{X_{1}}\to M_{X_{2}}\hat {\otimes }_{\mathcal {O}\left (X_{2}\right )} \mathcal {O}(X_{1})$
, which is a link and satisfies a cocycle condition. Then the eigenvarieties for
![]() $(\mathcal {O}(X), M_{X}, \mathbf {T}, \phi )$
can be patched into the eigenvariety
$(\mathcal {O}(X), M_{X}, \mathbf {T}, \phi )$
can be patched into the eigenvariety
![]() $\mathcal {E}\to Z_{\phi } \to \mathcal {W}$
[Reference Buzzard12, Construction 5.7], where
$\mathcal {E}\to Z_{\phi } \to \mathcal {W}$
[Reference Buzzard12, Construction 5.7], where
![]() $Z_{\phi }$
denotes the spectral variety over
$Z_{\phi }$
denotes the spectral variety over
![]() $\mathcal {W}$
constructed by gluing the spectral varieties over X.
$\mathcal {W}$
constructed by gluing the spectral varieties over X.
Let
![]() $L/K$
be an extension of complete valuation fields (of height
$L/K$
be an extension of complete valuation fields (of height
![]() $1$
). For any quasi-separated rigid analytic variety
$1$
). For any quasi-separated rigid analytic variety
![]() $\mathcal {X}$
over K and any coherent
$\mathcal {X}$
over K and any coherent
![]() $\mathcal {O}_{\mathcal {X}}$
-module
$\mathcal {O}_{\mathcal {X}}$
-module
![]() $\mathcal {F}$
, we can define base extensions
$\mathcal {F}$
, we can define base extensions
![]() $\mathcal {X}_{L}:=\mathcal {X} \hat {\otimes }_{K} L$
and
$\mathcal {X}_{L}:=\mathcal {X} \hat {\otimes }_{K} L$
and
![]() $\mathcal {F}_{L}$
of
$\mathcal {F}_{L}$
of
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $\mathcal {F}$
functorially (see [Reference Bosch, Güntzer and Remmert10, Section 9.3.6] and [Reference Conrad17, §3.1]). If the extension
$\mathcal {F}$
functorially (see [Reference Bosch, Güntzer and Remmert10, Section 9.3.6] and [Reference Conrad17, §3.1]). If the extension
![]() $L/K$
is finite, then they are just the fiber product and the pullback in the usual sense. Otherwise, it seems unclear if it has usual properties as a fiber product: for an open immersion
$L/K$
is finite, then they are just the fiber product and the pullback in the usual sense. Otherwise, it seems unclear if it has usual properties as a fiber product: for an open immersion
![]() $j: \mathcal {U}\to \mathcal {X}$
, what we know in this case is that the base extension
$j: \mathcal {U}\to \mathcal {X}$
, what we know in this case is that the base extension
![]() $j_{L}:\mathcal {U}_{L} \to \mathcal {X}_{L}$
is also an open immersion if j is quasi-compact (for example, if
$j_{L}:\mathcal {U}_{L} \to \mathcal {X}_{L}$
is also an open immersion if j is quasi-compact (for example, if
![]() $\mathcal {X}$
is quasi-separated and
$\mathcal {X}$
is quasi-separated and
![]() $\mathcal {U}$
is an admissible affinoid open subset) or a Zariski open immersion. At any rate, [Reference Bosch, Güntzer and Remmert10, Proposition 9.3.6/1 and Corollary 9.3.6/2] imply that the base extension takes any admissible affinoid covering of
$\mathcal {U}$
is an admissible affinoid open subset) or a Zariski open immersion. At any rate, [Reference Bosch, Güntzer and Remmert10, Proposition 9.3.6/1 and Corollary 9.3.6/2] imply that the base extension takes any admissible affinoid covering of
![]() $\mathcal {X}$
to that of
$\mathcal {X}$
to that of
![]() $\mathcal {X}_{L}$
. We write the set of L-valued points
$\mathcal {X}_{L}$
. We write the set of L-valued points
![]() $\mathcal {X}_{L}(L)$
also as
$\mathcal {X}_{L}(L)$
also as
![]() $\mathcal {X}(L)$
.
$\mathcal {X}(L)$
.
Let
![]() $(R,M,\mathbf {T},\phi )$
be an input datum for the eigenvariety machine over K and let
$(R,M,\mathbf {T},\phi )$
be an input datum for the eigenvariety machine over K and let
![]() $\mathcal {E}\to Z_{\phi }$
be the associated eigenvariety over
$\mathcal {E}\to Z_{\phi }$
be the associated eigenvariety over
![]() $X=\mathrm {Sp}(R)$
. We say that a K-algebra homomorphism
$X=\mathrm {Sp}(R)$
. We say that a K-algebra homomorphism
![]() $\lambda : \mathbf {T}\to L$
is an L-valued eigensystem in M if there exist an element
$\lambda : \mathbf {T}\to L$
is an L-valued eigensystem in M if there exist an element
![]() $x\in X(L)$
given by a K-algebra homomorphism
$x\in X(L)$
given by a K-algebra homomorphism
![]() $x^{*}: R\to L$
and a nonzero element m of
$x^{*}: R\to L$
and a nonzero element m of
![]() $M\hat {\otimes }_{R, x^{*}}L$
such that we have
$M\hat {\otimes }_{R, x^{*}}L$
such that we have
![]() $h m=\lambda (h) m$
for any
$h m=\lambda (h) m$
for any
![]() $h\in \mathbf {T}$
. It is said to be of finite slope if
$h\in \mathbf {T}$
. It is said to be of finite slope if
![]() $\lambda (\phi )\neq 0$
. Then there exists a natural bijection between
$\lambda (\phi )\neq 0$
. Then there exists a natural bijection between
![]() $\mathcal {E}(L)$
and the set of L-valued eigensystems
$\mathcal {E}(L)$
and the set of L-valued eigensystems
![]() $ \lambda $
in M of finite slopes [Reference Buzzard12, Lemma 5.9]. We state the following lemma for reference, which is in fact shown in [Reference Buzzard12]:
$ \lambda $
in M of finite slopes [Reference Buzzard12, Lemma 5.9]. We state the following lemma for reference, which is in fact shown in [Reference Buzzard12]:
Lemma 2.1. Let
![]() $(R,M,\mathbf {T},\phi )$
be an input datum for the eigenvariety machine over K and let
$(R,M,\mathbf {T},\phi )$
be an input datum for the eigenvariety machine over K and let
![]() $\mathcal {E}\to Z_{\phi }$
be the associated eigenvariety over
$\mathcal {E}\to Z_{\phi }$
be the associated eigenvariety over
![]() $X=\mathrm {Sp}(R)$
. Let
$X=\mathrm {Sp}(R)$
. Let
![]() $L/K$
be an extension of complete valuation fields and take
$L/K$
be an extension of complete valuation fields and take
![]() $z\in \mathcal {E}(L)$
. Let
$z\in \mathcal {E}(L)$
. Let
![]() $x\in X(L)$
and
$x\in X(L)$
and
![]() $y\in Z_{\phi }(L)$
be the images of z. Let
$y\in Z_{\phi }(L)$
be the images of z. Let
![]() $\lambda : \mathbf {T}\to L$
be the L-valued eigensystem in M corresponding to z. Let m be a nonzero element of
$\lambda : \mathbf {T}\to L$
be the L-valued eigensystem in M corresponding to z. Let m be a nonzero element of
![]() $M\hat {\otimes }_{R,x^{*}} L$
satisfying
$M\hat {\otimes }_{R,x^{*}} L$
satisfying
![]() $h m=\lambda (h) m$
for any
$h m=\lambda (h) m$
for any
![]() $h\in \mathbf {T}$
. Take an admissible affinoid open subset V in the canonical admissible covering of
$h\in \mathbf {T}$
. Take an admissible affinoid open subset V in the canonical admissible covering of
![]() $Z_{\phi }$
satisfying
$Z_{\phi }$
satisfying
![]() $y\in V(L)$
. Write
$y\in V(L)$
. Write
![]() $f(V)=\mathrm {Sp}(A)$
. Suppose
$f(V)=\mathrm {Sp}(A)$
. Suppose
![]() $f(V)$
is connected. Let
$f(V)$
is connected. Let
![]() $P(T)$
be the characteristic power series of
$P(T)$
be the characteristic power series of
![]() $\phi $
acting on M. Let
$\phi $
acting on M. Let
![]() $Q(T)$
be the factor of
$Q(T)$
be the factor of
![]() $P(T)$
in
$P(T)$
in
![]() $A\{\{T\}\}$
associated to V and let
$A\{\{T\}\}$
associated to V and let
![]() $M_{A}=N\oplus F$
be the corresponding decomposition of
$M_{A}=N\oplus F$
be the corresponding decomposition of
![]() $M_{A}$
, as before. Then we have the following:
$M_{A}$
, as before. Then we have the following:
-
(1)
 $\lambda (h)=h(z)$
in L, where
$\lambda (h)=h(z)$
in L, where
 $h(z)$
is the specialization at z of the image of h by the map
$h(z)$
is the specialization at z of the image of h by the map
 $\mathbf {T}\to \mathcal {O}(\mathcal {E})$
.
$\mathbf {T}\to \mathcal {O}(\mathcal {E})$
. -
(2) The decomposition
is the one corresponding to the factor $$ \begin{align*} M\hat{\otimes}_{R, x^{*}}L=N\otimes_{A, x^{*}}L\oplus F\hat{\otimes}_{A,x^{*}}L \end{align*} $$
$$ \begin{align*} M\hat{\otimes}_{R, x^{*}}L=N\otimes_{A, x^{*}}L\oplus F\hat{\otimes}_{A,x^{*}}L \end{align*} $$
 $Q_{x}(T)$
of
$Q_{x}(T)$
of
 $P_{x}(T)$
, where
$P_{x}(T)$
, where
 $P_{x}(T)$
and
$P_{x}(T)$
and
 $Q_{x}(T)$
are the images of
$Q_{x}(T)$
are the images of
 $P(T)$
and
$P(T)$
and
 $Q(T)$
in
$Q(T)$
in
 $L\{\{T\}\}$
by
$L\{\{T\}\}$
by
 $x^{*}$
, respectively.
$x^{*}$
, respectively.
-
(3)
 $Q_{x}\left (\lambda (\phi )^{-1}\right )=0$
and
$Q_{x}\left (\lambda (\phi )^{-1}\right )=0$
and
 $m\in N{\otimes }_{A,x^{*}} L$
.
$m\in N{\otimes }_{A,x^{*}} L$
.
Proof. The first assertion follows from the proof of [Reference Buzzard12, Lemma 5.9]. The second one follows from [Reference Buzzard12, Lemma 2.13] and the uniqueness of the decomposition in [Reference Buzzard12, Theorem 3.3]. For the third one, note that the definition of the map
![]() $\mathcal {E}(V)\to V$
implies
$\mathcal {E}(V)\to V$
implies
 $Q_{x}\left (\lambda (\phi )^{-1}\right )=Q_{x}^{*}(\lambda (\phi ))=0$
. Since
$Q_{x}\left (\lambda (\phi )^{-1}\right )=Q_{x}^{*}(\lambda (\phi ))=0$
. Since
![]() $Q_{x}^{*}(\phi )m=Q_{x}^{*}(\lambda (\phi ))m=0$
, the second assertion implies
$Q_{x}^{*}(\phi )m=Q_{x}^{*}(\lambda (\phi ))m=0$
, the second assertion implies
![]() $m \in N{\otimes }_{A,x^{*}} L$
.
$m \in N{\otimes }_{A,x^{*}} L$
.
2.2 Lifting lemma à la Deligne and Serre
In this subsection, we consider the problem of converting a family of eigensystems into a family of eigenforms. First we show a local lemma in the following setting: Let L be a complete valuation field which is algebraically closed. Let
![]() $(A,N,T,S,\varphi )$
be a tuple consisting of
$(A,N,T,S,\varphi )$
be a tuple consisting of
-
• an L-affinoid algebra A,
-
• a projective A-module N of finite rank,
-
• a finite A-algebra T equipped with an A-algebra homomorphism
 $T\to \mathrm {End}_{A}(N)$
,
$T\to \mathrm {End}_{A}(N)$
, -
• an L-affinoid algebra S which is an integral domain, and
-
• a homomorphism
 $\varphi : T\to S$
of L-affinoid algebras.
$\varphi : T\to S$
of L-affinoid algebras.
For any
![]() $x\in \mathrm {Sp}(S)$
, we write
$x\in \mathrm {Sp}(S)$
, we write
![]() $m_{x}$
for the associated maximal ideal of S.
$m_{x}$
for the associated maximal ideal of S.
Lemma 2.2. Let L be a complete valuation field which is algebraically closed. Let
![]() $(A,N,T,S,\varphi )$
be a tuple as before. Assume that for any
$(A,N,T,S,\varphi )$
be a tuple as before. Assume that for any
![]() $x\in \mathrm {Sp}(S)$
, the induced map
$x\in \mathrm {Sp}(S)$
, the induced map
is an
![]() $S/m_{x}$
-valued eigensystem in N. Namely, we assume that for any
$S/m_{x}$
-valued eigensystem in N. Namely, we assume that for any
![]() $x\in \mathrm {Sp}(S)$
, there exists a nonzero element
$x\in \mathrm {Sp}(S)$
, there exists a nonzero element
![]() $f_{x}\in N\otimes _{A} S/m_{x}$
satisfying
$f_{x}\in N\otimes _{A} S/m_{x}$
satisfying
![]() $(h\otimes 1) f_{x}=(1\otimes \varphi (h)(x))f_{x}$
for any
$(h\otimes 1) f_{x}=(1\otimes \varphi (h)(x))f_{x}$
for any
![]() $h\in T$
.
$h\in T$
.
-
(1) There exists a nonzero element
 $F\in N\otimes _{A} S$
satisfying
$F\in N\otimes _{A} S$
satisfying
 $(h\otimes 1)F=(1\otimes \varphi (h))F$
for any
$(h\otimes 1)F=(1\otimes \varphi (h))F$
for any
 $h\in T$
.
$h\in T$
. -
(2) Assume moreover that S is a principal ideal domain. We write
 $F(x)$
for the image of F in
$F(x)$
for the image of F in
 $N\otimes _{A} S/m_{x}$
. Then there exists F as in (1) satisfying
$N\otimes _{A} S/m_{x}$
. Then there exists F as in (1) satisfying
 $F(x)\neq 0$
for any
$F(x)\neq 0$
for any
 $x\in \mathrm {Sp}(S)$
.
$x\in \mathrm {Sp}(S)$
.
Proof. Put
![]() $P=\mathrm {Ker}(\varphi : T\to S)$
, which is a prime ideal of T. Consider the multiplication map
$P=\mathrm {Ker}(\varphi : T\to S)$
, which is a prime ideal of T. Consider the multiplication map
![]() $\mu :T\otimes _{A}T/P\to T/P$
, and put
$\mu :T\otimes _{A}T/P\to T/P$
, and put
Then the ideal Q is a minimal prime ideal. Indeed, since the A-algebra T is finite, the
![]() $T/P$
-algebra
$T/P$
-algebra
![]() $T\otimes _{A} T/P$
is also finite, and thus the latter ring is a finite extension of a quotient of
$T\otimes _{A} T/P$
is also finite, and thus the latter ring is a finite extension of a quotient of
![]() $T/P$
. Since the quotient
$T/P$
. Since the quotient
![]() $(T\otimes _{A} T/P)/Q$
is isomorphic to
$(T\otimes _{A} T/P)/Q$
is isomorphic to
![]() $T/P$
, we have the inequality
$T/P$
, we have the inequality
which implies
![]() $\mathrm {ht}(Q)=0$
.
$\mathrm {ht}(Q)=0$
.
The ideals
![]() $n_{x}=\varphi ^{-1}(m_{x})$
and
$n_{x}=\varphi ^{-1}(m_{x})$
and
![]() $\bar {n}^{\prime }_{x}=(\varphi \circ \mu )^{-1}(m_{x})$
are maximal ideals of the rings T and
$\bar {n}^{\prime }_{x}=(\varphi \circ \mu )^{-1}(m_{x})$
are maximal ideals of the rings T and
![]() $T\otimes _{A} T/P$
, respectively. We write
$T\otimes _{A} T/P$
, respectively. We write
![]() $\bar {n}_{x}$
for the inverse image of
$\bar {n}_{x}$
for the inverse image of
![]() $m_{x}$
by the map
$m_{x}$
by the map
![]() $T/P\to S$
, which is also a maximal ideal. Via the map
$T/P\to S$
, which is also a maximal ideal. Via the map
![]() $1\otimes \varphi : T\otimes _{A} T/P\to T\otimes _{A} S$
, the ring
$1\otimes \varphi : T\otimes _{A} T/P\to T\otimes _{A} S$
, the ring
![]() $T\otimes _{A} T/P$
acts on
$T\otimes _{A} T/P$
acts on
![]() $N\otimes _{A} S/m_{x}$
for any
$N\otimes _{A} S/m_{x}$
for any
![]() $x\in \mathrm {Sp}(S)$
.
$x\in \mathrm {Sp}(S)$
.
First we claim that
![]() $\bar {n}^{\prime }_{x}=\mathrm {Ann}_{T\otimes _{A} T/P}(f_{x})$
. Since
$\bar {n}^{\prime }_{x}=\mathrm {Ann}_{T\otimes _{A} T/P}(f_{x})$
. Since
![]() $\bar {n}^{\prime }_{x}$
is a maximal ideal and
$\bar {n}^{\prime }_{x}$
is a maximal ideal and
![]() $f_{x}\neq 0$
, it is enough to show
$f_{x}\neq 0$
, it is enough to show
![]() $\bar {n}^{\prime }_{x}\subseteq \mathrm {Ann}_{T\otimes _{A} T/P}(f_{x})$
. Since L is algebraically closed, the ideal
$\bar {n}^{\prime }_{x}\subseteq \mathrm {Ann}_{T\otimes _{A} T/P}(f_{x})$
. Since L is algebraically closed, the ideal
![]() $\mathrm {Im}(n_{x}\otimes _{A} T/P)+\mathrm {Im}(T\otimes _{A} \bar {n}_{x})$
is a maximal ideal contained in
$\mathrm {Im}(n_{x}\otimes _{A} T/P)+\mathrm {Im}(T\otimes _{A} \bar {n}_{x})$
is a maximal ideal contained in
![]() $\bar {n}^{\prime }_{x}$
, and thus they are equal. For any
$\bar {n}^{\prime }_{x}$
, and thus they are equal. For any
![]() $h\in T$
, we denote its image in
$h\in T$
, we denote its image in
![]() $T/P$
by
$T/P$
by
![]() $\bar {h}$
. Take elements
$\bar {h}$
. Take elements
![]() $h\in T$
and
$h\in T$
and
![]() $h^{\prime }\in n_{x}$
. We have
$h^{\prime }\in n_{x}$
. We have
 $\left (h\otimes \bar {h}^{\prime }\right ) f_{x}=0$
. On the other hand, we also have
$\left (h\otimes \bar {h}^{\prime }\right ) f_{x}=0$
. On the other hand, we also have
![]() $(h^{\prime }\otimes 1)f_{x}=(1\otimes \varphi (h^{\prime })(x))f_{x}=0$
by assumption. This implies
$(h^{\prime }\otimes 1)f_{x}=(1\otimes \varphi (h^{\prime })(x))f_{x}=0$
by assumption. This implies
 $\left (h^{\prime }\otimes \bar {h}\right )f_{x}=0$
, and the claim follows.
$\left (h^{\prime }\otimes \bar {h}\right )f_{x}=0$
, and the claim follows.
Next we claim that the localization
![]() $(N\otimes _{A} T/P)_{Q}$
of the
$(N\otimes _{A} T/P)_{Q}$
of the
![]() $T\otimes _{A} T/P$
-module
$T\otimes _{A} T/P$
-module
![]() $N\otimes _{A} T/P$
at Q is nonzero. Suppose the contrary. Since the
$N\otimes _{A} T/P$
at Q is nonzero. Suppose the contrary. Since the
![]() $T\otimes _{A} T/P$
-module
$T\otimes _{A} T/P$
-module
![]() $N\otimes _{A} T/P$
is finite, we can find
$N\otimes _{A} T/P$
is finite, we can find
![]() $s\notin Q$
satisfying
$s\notin Q$
satisfying
![]() $s(N\otimes _{A} T/P)=0$
. Take any
$s(N\otimes _{A} T/P)=0$
. Take any
![]() $x\in \mathrm {Sp}(S)$
. We have
$x\in \mathrm {Sp}(S)$
. We have
![]() $s(N\otimes _{A} T/n_{x})=0$
. Since L is algebraically closed, we have
$s(N\otimes _{A} T/n_{x})=0$
. Since L is algebraically closed, we have
![]() $L=T/n_{x}=S/m_{x}$
, and we also see that
$L=T/n_{x}=S/m_{x}$
, and we also see that
![]() $s(N\otimes _{A} S/m_{x})=0$
. In particular, we have
$s(N\otimes _{A} S/m_{x})=0$
. In particular, we have
![]() $sf_{x}=0$
and
$sf_{x}=0$
and
![]() $s\in \mathrm {Ann}_{T\otimes _{A} T/P}(f_{x})=\bar {n}^{\prime }_{x}$
. Thus we obtain
$s\in \mathrm {Ann}_{T\otimes _{A} T/P}(f_{x})=\bar {n}^{\prime }_{x}$
. Thus we obtain
 $$ \begin{align*} s\in \bigcap_{x \in \mathrm{Sp}(S)} \bar{n}^{\prime}_{x}=\bigcap_{x \in \mathrm{Sp}(S)} (\varphi\circ \mu)^{-1}(m_{x})= (\varphi\circ \mu)^{-1}\left(\bigcap_{x \in \mathrm{Sp}(S)} m_{x}\right). \end{align*} $$
$$ \begin{align*} s\in \bigcap_{x \in \mathrm{Sp}(S)} \bar{n}^{\prime}_{x}=\bigcap_{x \in \mathrm{Sp}(S)} (\varphi\circ \mu)^{-1}(m_{x})= (\varphi\circ \mu)^{-1}\left(\bigcap_{x \in \mathrm{Sp}(S)} m_{x}\right). \end{align*} $$
The assumption that S is a reduced L-affinoid algebra implies
 $$ \begin{align*} \bigcap_{x \in \mathrm{Sp}(S)} m_{x}=0. \end{align*} $$
$$ \begin{align*} \bigcap_{x \in \mathrm{Sp}(S)} m_{x}=0. \end{align*} $$
Hence
![]() $s\in \mathrm {Ker}(\varphi \circ \mu )=Q$
, which is a contradiction.
$s\in \mathrm {Ker}(\varphi \circ \mu )=Q$
, which is a contradiction.
Therefore we obtain
![]() $Q\in \mathrm {Supp}_{T\otimes _{A} T/P}(N\otimes _{A} T/P)$
. Since Q is a minimal prime ideal, it is also contained in
$Q\in \mathrm {Supp}_{T\otimes _{A} T/P}(N\otimes _{A} T/P)$
. Since Q is a minimal prime ideal, it is also contained in
![]() $\mathrm {Ass}_{T\otimes _{A} T/P}(N\otimes _{A} T/P)$
. Namely, the prime ideal Q is written as
$\mathrm {Ass}_{T\otimes _{A} T/P}(N\otimes _{A} T/P)$
. Namely, the prime ideal Q is written as
![]() $Q=\mathrm {Ann}_{T\otimes _{A} T/P}(G)$
with some nonzero element G of
$Q=\mathrm {Ann}_{T\otimes _{A} T/P}(G)$
with some nonzero element G of
![]() $N\otimes _{A} T/P$
. Since the A-module N is projective, the natural map
$N\otimes _{A} T/P$
. Since the A-module N is projective, the natural map
![]() $1\otimes \varphi : N\otimes _{A} T/P\to N\otimes _{A} S$
is an injection. Thus the image
$1\otimes \varphi : N\otimes _{A} T/P\to N\otimes _{A} S$
is an injection. Thus the image
![]() $F=(1\otimes \varphi )(G)$
is nonzero. Moreover, since
$F=(1\otimes \varphi )(G)$
is nonzero. Moreover, since
![]() $h\otimes 1-1\otimes \bar {h}\in Q$
for any
$h\otimes 1-1\otimes \bar {h}\in Q$
for any
![]() $h\in T$
, we have the equality
$h\in T$
, we have the equality
 $(h\otimes 1)G=\left (1\otimes \bar {h}\right )G$
. Hence we obtain
$(h\otimes 1)G=\left (1\otimes \bar {h}\right )G$
. Hence we obtain
![]() $(h\otimes 1)F=(1\otimes \varphi (h))F$
, and assertion (1) follows.
$(h\otimes 1)F=(1\otimes \varphi (h))F$
, and assertion (1) follows.
Now assume that S is a principal ideal domain. Then each maximal ideal
![]() $m_{x}$
of S is generated by a single element
$m_{x}$
of S is generated by a single element
![]() $t_{x}$
. Put
$t_{x}$
. Put
Since the A-module N is projective and the Krull dimension of S is no more than
![]() $1$
, we see that
$1$
, we see that
![]() $\Sigma (F)$
is a finite set. For any
$\Sigma (F)$
is a finite set. For any
![]() $x\in \Sigma (F)$
, the element F lies in
$x\in \Sigma (F)$
, the element F lies in
![]() $\mathrm {Ker}(N\otimes _{A} S\to N\otimes _{A} S/m_{x})=m_{x}(N\otimes _{A} S)$
. By Krull’s intersection theorem, there exists a positive integer
$\mathrm {Ker}(N\otimes _{A} S\to N\otimes _{A} S/m_{x})=m_{x}(N\otimes _{A} S)$
. By Krull’s intersection theorem, there exists a positive integer
![]() $c_{x}$
satisfying
$c_{x}$
satisfying
![]() $F\in t_{x}^{c_{x}} (N\otimes _{A} S)\setminus t_{x}^{c_{x}+1} (N\otimes _{A} S)$
. Put
$F\in t_{x}^{c_{x}} (N\otimes _{A} S)\setminus t_{x}^{c_{x}+1} (N\otimes _{A} S)$
. Put
![]() $F=t_{x}^{c_{x}} H$
with some nonzero element H of
$F=t_{x}^{c_{x}} H$
with some nonzero element H of
![]() $N\otimes _{A} S$
. We have
$N\otimes _{A} S$
. We have
![]() $H(x)\neq 0$
and
$H(x)\neq 0$
and
![]() $\Sigma (H)\subsetneq \Sigma (F)$
. Since the S-module
$\Sigma (H)\subsetneq \Sigma (F)$
. Since the S-module
![]() $N\otimes _{A} S$
is torsion free, the element H also satisfies
$N\otimes _{A} S$
is torsion free, the element H also satisfies
![]() $(h\otimes 1)H=(1\otimes \varphi (h))H$
for any
$(h\otimes 1)H=(1\otimes \varphi (h))H$
for any
![]() $h\in T$
. Repeating this, we can find F as in assertion (1) satisfying
$h\in T$
. Repeating this, we can find F as in assertion (1) satisfying
![]() $\Sigma (F)=\emptyset $
.
$\Sigma (F)=\emptyset $
.
Remark 2.3. Let
![]() $\mathrm {Sp}(S)$
be a connected affinoid subdomain of the unit disc
$\mathrm {Sp}(S)$
be a connected affinoid subdomain of the unit disc
![]() $\mathcal {D}_{\mathbb {C}_{p}}=\mathrm {Sp}\left (\mathbb {C}_{p}\langle T\rangle \right )$
. Note that
$\mathcal {D}_{\mathbb {C}_{p}}=\mathrm {Sp}\left (\mathbb {C}_{p}\langle T\rangle \right )$
. Note that
![]() $\mathbb {C}_{p}\langle T\rangle $
is a principal ideal domain, since it is a unique factorization domain of Krull dimension
$\mathbb {C}_{p}\langle T\rangle $
is a principal ideal domain, since it is a unique factorization domain of Krull dimension
![]() $1$
. [Reference Bosch, Güntzer and Remmert10, Proposition 7.2.2/1] implies that S is a regular ring of Krull dimension no more than
$1$
. [Reference Bosch, Güntzer and Remmert10, Proposition 7.2.2/1] implies that S is a regular ring of Krull dimension no more than
![]() $1$
such that every maximal ideal is principal. Since
$1$
such that every maximal ideal is principal. Since
![]() $\mathrm {Sp}(S)$
is connected, we see that S is a principal ideal domain. Hence the assumption of Lemma 2.2(2) is satisfied in this case.
$\mathrm {Sp}(S)$
is connected, we see that S is a principal ideal domain. Hence the assumption of Lemma 2.2(2) is satisfied in this case.
We say that a rigid analytic variety X is principally refined if any admissible covering of X has a refinement by an admissible affinoid covering
![]() $X=\bigcup _{i\in I} U_{i}$
such that the affinoid algebra of each affinoid open subset
$X=\bigcup _{i\in I} U_{i}$
such that the affinoid algebra of each affinoid open subset
![]() $U_{i}$
in the refined covering is a principal ideal domain.
$U_{i}$
in the refined covering is a principal ideal domain.
Remark 2.4. Remark 2.3 implies that any open subvariety of
![]() $\mathcal {D}_{\mathbb {C}_{p}}$
is principally refined.
$\mathcal {D}_{\mathbb {C}_{p}}$
is principally refined.
For the eigenvariety associated to an input datum
![]() $(R,M,\mathbf {T},\phi )$
, Lemma 2.2 implies the following proposition:
$(R,M,\mathbf {T},\phi )$
, Lemma 2.2 implies the following proposition:
Proposition 2.5. Let
![]() $(R,M,\mathbf {T},\phi )$
be an input datum for the eigenvariety machine over K and let
$(R,M,\mathbf {T},\phi )$
be an input datum for the eigenvariety machine over K and let
![]() $\mathcal {E}\to Z_{\phi }\to \mathrm {Sp}(R)$
be the associated eigenvariety. Let
$\mathcal {E}\to Z_{\phi }\to \mathrm {Sp}(R)$
be the associated eigenvariety. Let
![]() $L/K$
be an extension of complete valuation fields such that L is algebraically closed. Let X be a smooth rigid analytic variety over L and let
$L/K$
be an extension of complete valuation fields such that L is algebraically closed. Let X be a smooth rigid analytic variety over L and let
![]() $\varphi : X \to \mathcal {E}_{L}=\mathcal {E}\hat {\otimes }_{K} L$
be a morphism of rigid analytic varieties over L.
$\varphi : X \to \mathcal {E}_{L}=\mathcal {E}\hat {\otimes }_{K} L$
be a morphism of rigid analytic varieties over L.
-
(1) There exist an admissible affinoid covering
 $X=\bigcup _{i\in I} U_{i}$
and a nonzero element
$X=\bigcup _{i\in I} U_{i}$
and a nonzero element
 $F_{i}\in M\hat {\otimes }_{R} \mathcal {O}(U_{i})$
for each
$F_{i}\in M\hat {\otimes }_{R} \mathcal {O}(U_{i})$
for each
 $i\in I$
satisfying
$i\in I$
satisfying
 $(h\otimes 1)F_{i}=(1\otimes \varphi ^{*}(h))F_{i}$
for any
$(h\otimes 1)F_{i}=(1\otimes \varphi ^{*}(h))F_{i}$
for any
 $h\in \mathbf {T}$
, where
$h\in \mathbf {T}$
, where
 $\varphi ^{*}: \mathbf {T}\to \mathcal {O}(\mathcal {E})\to \mathcal {O}(U_{i})$
is the map induced by
$\varphi ^{*}: \mathbf {T}\to \mathcal {O}(\mathcal {E})\to \mathcal {O}(U_{i})$
is the map induced by
 $\varphi $
.
$\varphi $
. -
(2) Assume moreover that X is principally refined. We write
 $k(x)$
for the residue field of
$k(x)$
for the residue field of
 $x\in U_{i}$
and
$x\in U_{i}$
and
 $F_{i}(x)$
for the image of
$F_{i}(x)$
for the image of
 $F_{i}$
in
$F_{i}$
in
 $M\hat {\otimes }_{R} k(x)$
. Then we can find
$M\hat {\otimes }_{R} k(x)$
. Then we can find
 $F_{i}$
as in (1) satisfying
$F_{i}$
as in (1) satisfying
 $F_{i}(x)\neq 0$
for any
$F_{i}(x)\neq 0$
for any
 $x\in U_{i}$
.
$x\in U_{i}$
.
Proof. Let
![]() $\mathcal {C}$
be the canonical admissible covering of
$\mathcal {C}$
be the canonical admissible covering of
![]() $Z_{\phi }$
. For any
$Z_{\phi }$
. For any
![]() $V\in \mathcal {C}$
, we have the K-affinoid variety
$V\in \mathcal {C}$
, we have the K-affinoid variety
![]() $\mathcal {E}(V)=\mathrm {Sp}(\mathbf {T}(V))$
, as before. Then
$\mathcal {E}(V)=\mathrm {Sp}(\mathbf {T}(V))$
, as before. Then
![]() $\mathcal {E}_{L} =\bigcup _{V\in \mathcal {C}} \mathcal {E}(V)_{L}$
is an admissible affinoid covering of
$\mathcal {E}_{L} =\bigcup _{V\in \mathcal {C}} \mathcal {E}(V)_{L}$
is an admissible affinoid covering of
![]() $\mathcal {E}_{L}$
. Let
$\mathcal {E}_{L}$
. Let
![]() $f:Z_{\phi }\to \mathrm {Sp}(R)$
be the natural projection and write
$f:Z_{\phi }\to \mathrm {Sp}(R)$
be the natural projection and write
![]() $f(V)=\mathrm {Sp}(A)$
. For any
$f(V)=\mathrm {Sp}(A)$
. For any
![]() $V\in \mathcal {C}$
such that
$V\in \mathcal {C}$
such that
![]() $f(V)$
is connected, take an admissible affinoid covering
$f(V)$
is connected, take an admissible affinoid covering
 $\varphi ^{-1}(\mathcal {E}(V)_{L})=\bigcup _{i\in I_{V}} U_{i}$
such that
$\varphi ^{-1}(\mathcal {E}(V)_{L})=\bigcup _{i\in I_{V}} U_{i}$
such that
![]() $U_{i}=\mathrm {Sp}(S_{i})$
is connected for any
$U_{i}=\mathrm {Sp}(S_{i})$
is connected for any
![]() $i\in I_{V}$
. From the construction of the eigenvariety, we have a natural decomposition
$i\in I_{V}$
. From the construction of the eigenvariety, we have a natural decomposition
![]() $M\hat {\otimes }_{R} A=N\oplus F$
into closed A-submodules N and F. Note that the A-module N is finite and projective. Since the complete tensor product commutes with the direct sum, the
$M\hat {\otimes }_{R} A=N\oplus F$
into closed A-submodules N and F. Note that the A-module N is finite and projective. Since the complete tensor product commutes with the direct sum, the
![]() $S_{i}$
-module
$S_{i}$
-module
![]() $N\otimes _{A} S_{i}$
is a submodule of
$N\otimes _{A} S_{i}$
is a submodule of
![]() $M\hat {\otimes }_{R} S_{i}$
.
$M\hat {\otimes }_{R} S_{i}$
.
For any
![]() $i\in I_{V}$
, consider the natural map
$i\in I_{V}$
, consider the natural map
![]() $\varphi ^{*}: \mathbf {T}\to \mathbf {T}(V)\to S_{i}$
. We denote the map
$\varphi ^{*}: \mathbf {T}\to \mathbf {T}(V)\to S_{i}$
. We denote the map
![]() $\mathbf {T}(V)\to S_{i}$
also by
$\mathbf {T}(V)\to S_{i}$
also by
![]() $\varphi ^{*}$
. For any
$\varphi ^{*}$
. For any
![]() $x\in U_{i}=\mathrm {Sp}(S_{i})$
, the composite
$x\in U_{i}=\mathrm {Sp}(S_{i})$
, the composite
![]() $\mathrm {Sp}(k(x))\to U_{i}\to \mathcal {E}_{L}$
corresponds to a
$\mathrm {Sp}(k(x))\to U_{i}\to \mathcal {E}_{L}$
corresponds to a
![]() $k(x)$
-valued eigensystem of
$k(x)$
-valued eigensystem of
![]() $\mathbf {T}$
in M of finite slope. Namely, there exists a nonzero element
$\mathbf {T}$
in M of finite slope. Namely, there exists a nonzero element
![]() $g_{x}$
of
$g_{x}$
of
![]() $M\hat {\otimes }_{R} k(x)=N{\otimes }_{A} k(x)\oplus F\hat {\otimes }_{A} k(x)$
satisfying
$M\hat {\otimes }_{R} k(x)=N{\otimes }_{A} k(x)\oplus F\hat {\otimes }_{A} k(x)$
satisfying
![]() $(h\otimes 1)g_{x}=(1\otimes \varphi ^{*}(h)(x)) g_{x}$
for any
$(h\otimes 1)g_{x}=(1\otimes \varphi ^{*}(h)(x)) g_{x}$
for any
![]() $h\in \mathbf {T}$
and
$h\in \mathbf {T}$
and
![]() $(\phi \otimes 1)g_{x}\neq 0$
. Lemma 2.1(3) implies
$(\phi \otimes 1)g_{x}\neq 0$
. Lemma 2.1(3) implies
![]() $g_{x}\in N{\otimes }_{A} k(x)$
. Since
$g_{x}\in N{\otimes }_{A} k(x)$
. Since
![]() $U_{i}$
is connected and smooth, the ring
$U_{i}$
is connected and smooth, the ring
![]() $S_{i}$
is an integral domain. Applying Lemma 2.2(1) to the tuple
$S_{i}$
is an integral domain. Applying Lemma 2.2(1) to the tuple
 $\left (A\hat {\otimes }_{K} L,N\hat {\otimes }_{K} L,\mathbf {T}(V)\hat {\otimes }_{K} L, S_{i},\varphi ^{*}\otimes 1\right )$
, we obtain a nonzero element
$\left (A\hat {\otimes }_{K} L,N\hat {\otimes }_{K} L,\mathbf {T}(V)\hat {\otimes }_{K} L, S_{i},\varphi ^{*}\otimes 1\right )$
, we obtain a nonzero element
 $G_{i}\in N\otimes _{A} S_{i}=\left (N\hat {\otimes }_{K} L\right )\hat {\otimes }_{A\hat {\otimes }_{K} L} S_{i}$
satisfying
$G_{i}\in N\otimes _{A} S_{i}=\left (N\hat {\otimes }_{K} L\right )\hat {\otimes }_{A\hat {\otimes }_{K} L} S_{i}$
satisfying
![]() $(h\otimes 1)G_{i}=(1\otimes \varphi ^{*}(h))G_{i}$
for any
$(h\otimes 1)G_{i}=(1\otimes \varphi ^{*}(h))G_{i}$
for any
![]() $h\in \mathbf {T}$
. Setting
$h\in \mathbf {T}$
. Setting
![]() $F_{i}$
to be the image of
$F_{i}$
to be the image of
![]() $G_{i}$
by the injection
$G_{i}$
by the injection
![]() $N\otimes _{A} S_{i} \to M\hat {\otimes }_{R} S_{i}$
assertion (1) follows.
$N\otimes _{A} S_{i} \to M\hat {\otimes }_{R} S_{i}$
assertion (1) follows.
For assertion (2), by assumption we may assume that each
![]() $S_{i}$
is a principal domain. Then Lemma 2.2(2) allows us to find
$S_{i}$
is a principal domain. Then Lemma 2.2(2) allows us to find
![]() $G_{i}$
satisfying in addition
$G_{i}$
satisfying in addition
![]() $G_{i}(x)\neq 0$
for any
$G_{i}(x)\neq 0$
for any
![]() $x\in U_{i}$
. Since we have a commutative diagram
$x\in U_{i}$
. Since we have a commutative diagram

such that the horizontal arrows are injective, we obtain
![]() $F_{i}(x)\neq 0$
for any
$F_{i}(x)\neq 0$
for any
![]() $x\in U_{i}$
.
$x\in U_{i}$
.
2.3 Bellaïche and Chenevier’s argument
Let
![]() $(R,M,\mathbf {T},\phi )$
be an input datum for the eigenvariety machine over K and let
$(R,M,\mathbf {T},\phi )$
be an input datum for the eigenvariety machine over K and let
![]() $\mathcal {E}\to Z_{\phi }\to \mathrm {Sp}(R)$
be the associated eigenvariety. Let
$\mathcal {E}\to Z_{\phi }\to \mathrm {Sp}(R)$
be the associated eigenvariety. Let
![]() $L/K$
be an extension of complete valuation fields. Put
$L/K$
be an extension of complete valuation fields. Put
![]() $R_{L}=R\hat {\otimes }_{K} L$
. Let X be a rigid analytic variety over L equipped with a morphism
$R_{L}=R\hat {\otimes }_{K} L$
. Let X be a rigid analytic variety over L equipped with a morphism
![]() $\kappa : X\to \mathrm {Sp}(R_{L})$
. For any
$\kappa : X\to \mathrm {Sp}(R_{L})$
. For any
![]() $x\in X$
, we have a natural ring homomorphism
$x\in X$
, we have a natural ring homomorphism
![]() $\kappa ^{*}(x): R\to k(x)$
. A ring homomorphism
$\kappa ^{*}(x): R\to k(x)$
. A ring homomorphism
![]() $\varphi : \mathbf {T}\to \mathcal {O}(X)$
is said to be a family of eigensystems in M over X if, for any
$\varphi : \mathbf {T}\to \mathcal {O}(X)$
is said to be a family of eigensystems in M over X if, for any
![]() $x\in X$
, there exists a nonzero element
$x\in X$
, there exists a nonzero element
![]() $f_{x}$
of
$f_{x}$
of
 $M\hat {\otimes }_{R,\kappa ^{*}(x)} k(x)$
such that
$M\hat {\otimes }_{R,\kappa ^{*}(x)} k(x)$
such that
![]() $(h\otimes 1)f_{x}=(1\otimes \varphi (h)(x))f_{x}$
for any
$(h\otimes 1)f_{x}=(1\otimes \varphi (h)(x))f_{x}$
for any
![]() $h\in \mathbf {T}$
. It is said to be of finite slopes if
$h\in \mathbf {T}$
. It is said to be of finite slopes if
![]() $\varphi (\phi )(x)\neq 0$
for any
$\varphi (\phi )(x)\neq 0$
for any
![]() $x\in X$
. This is the same as saying that
$x\in X$
. This is the same as saying that
![]() $\varphi (\phi )\in \mathcal {O}(X)^{\times }$
. In this subsection, we show that we can convert a family of eigensystems of finite slopes over a reduced base space into a morphism to the eigenvariety, following [Reference Bellaïche and Chenevier7, Proposition 7.2.8]. First we recall the following lemma:
$\varphi (\phi )\in \mathcal {O}(X)^{\times }$
. In this subsection, we show that we can convert a family of eigensystems of finite slopes over a reduced base space into a morphism to the eigenvariety, following [Reference Bellaïche and Chenevier7, Proposition 7.2.8]. First we recall the following lemma:
Lemma 2.6.
-
(1) Let
 $f:X\to Y$
be a morphism of rigid analytic varieties over L with X reduced. Let Z be a closed analytic subvariety of Y. Suppose
$f:X\to Y$
be a morphism of rigid analytic varieties over L with X reduced. Let Z be a closed analytic subvariety of Y. Suppose
 $f(X)\subseteq Z$
. Then f factors through Z.
$f(X)\subseteq Z$
. Then f factors through Z. -
(2) Let
 $f,f^{\prime }:X\to Y$
be two morphisms of rigid analytic varieties over L with X reduced and Y separated. Suppose that these morphisms define the same map between the underlying sets. Then
$f,f^{\prime }:X\to Y$
be two morphisms of rigid analytic varieties over L with X reduced and Y separated. Suppose that these morphisms define the same map between the underlying sets. Then
 $f=f^{\prime }$
.
$f=f^{\prime }$
.
Proof. For the first assertion, we may assume that
![]() $X=\mathrm {Sp}(R_{1})$
,
$X=\mathrm {Sp}(R_{1})$
,
![]() $Y=\mathrm {Sp}(R_{2})$
, and
$Y=\mathrm {Sp}(R_{2})$
, and
![]() $Z=\mathrm {Sp}(R_{2}/I)$
for some ideal I of
$Z=\mathrm {Sp}(R_{2}/I)$
for some ideal I of
![]() $R_{2}$
. Consider the associated ring homomorphism
$R_{2}$
. Consider the associated ring homomorphism
![]() $f^{*}: R_{2}\to R_{1}$
and put
$f^{*}: R_{2}\to R_{1}$
and put
![]() $J=\mathrm {Ker}(f^{*})$
. By assumption, every maximal ideal m of
$J=\mathrm {Ker}(f^{*})$
. By assumption, every maximal ideal m of
![]() $R_{1}$
satisfies
$R_{1}$
satisfies
![]() $(f^{*})^{-1}(m)\supseteq I$
. Since
$(f^{*})^{-1}(m)\supseteq I$
. Since
![]() $R_{1}$
is Jacobson and reduced, we obtain
$R_{1}$
is Jacobson and reduced, we obtain
 $$ \begin{align*} I\subseteq \bigcap_{m\in \mathrm{Sp}\left(R_{1}\right)} (f^{*})^{-1}(m)=(f^{*})^{-1}\left(\bigcap_{m\in \mathrm{Sp}\left(R_{1}\right)} m\right)=(f^{*})^{-1}(0)=J. \end{align*} $$
$$ \begin{align*} I\subseteq \bigcap_{m\in \mathrm{Sp}\left(R_{1}\right)} (f^{*})^{-1}(m)=(f^{*})^{-1}\left(\bigcap_{m\in \mathrm{Sp}\left(R_{1}\right)} m\right)=(f^{*})^{-1}(0)=J. \end{align*} $$
Hence assertion (1) follows. Assertion (2) follows from the first one applied to
![]() $(f,f^{\prime }):X\to Y\times _{L} Y$
and the diagonal
$(f,f^{\prime }):X\to Y\times _{L} Y$
and the diagonal
![]() $Y\to Y\times _{L} Y$
.
$Y\to Y\times _{L} Y$
.
Proposition 2.7. Let
![]() $(R,M,\mathbf {T},\phi )$
be an input datum for the eigenvariety machine over K and let
$(R,M,\mathbf {T},\phi )$
be an input datum for the eigenvariety machine over K and let
![]() $\mathcal {E}\to Z_{\phi }\to \mathrm {Sp}(R)$
be the associated eigenvariety. Let
$\mathcal {E}\to Z_{\phi }\to \mathrm {Sp}(R)$
be the associated eigenvariety. Let
![]() $L/K$
be an extension of complete valuation fields. Let X be a reduced rigid analytic variety over L equipped with a morphism
$L/K$
be an extension of complete valuation fields. Let X be a reduced rigid analytic variety over L equipped with a morphism
![]() $\kappa : X\to \mathrm {Sp}(R_{L})$
. Suppose that we have a family of eigensystems of finite slopes
$\kappa : X\to \mathrm {Sp}(R_{L})$
. Suppose that we have a family of eigensystems of finite slopes
![]() $\varphi : \mathbf {T}\to \mathcal {O}(X)$
in M over X. Then there exists a unique morphism
$\varphi : \mathbf {T}\to \mathcal {O}(X)$
in M over X. Then there exists a unique morphism
![]() $\Phi :X\to \mathcal {E}_{L}$
such that the diagram
$\Phi :X\to \mathcal {E}_{L}$
such that the diagram

is commutative and, for any
![]() $x\in X$
, the eigensystem over
$x\in X$
, the eigensystem over
![]() $k(x)$
corresponding to
$k(x)$
corresponding to
 $\mathrm {Sp}(k(x))\to X\overset {\Phi }{\to } \mathcal {E}_{L}$
is the map
$\mathrm {Sp}(k(x))\to X\overset {\Phi }{\to } \mathcal {E}_{L}$
is the map
![]() $\varphi (-)(x): \mathbf {T}\to k(x)$
.
$\varphi (-)(x): \mathbf {T}\to k(x)$
.
Proof. Let
![]() $\mathcal {C}$
be the canonical admissible covering of
$\mathcal {C}$
be the canonical admissible covering of
![]() $Z_{\phi }$
. Take any
$Z_{\phi }$
. Take any
![]() $V=\mathrm {Sp}(B)\in \mathcal {C}$
and put
$V=\mathrm {Sp}(B)\in \mathcal {C}$
and put
![]() $f(V)=\mathrm {Sp}(A)$
as in the proof of Proposition 2.5. Let I be a finite subset of
$f(V)=\mathrm {Sp}(A)$
as in the proof of Proposition 2.5. Let I be a finite subset of
![]() $\mathbf {T}$
such that its image in
$\mathbf {T}$
such that its image in
![]() $\mathbf {T}(V)$
is a system of generators of the finite B-algebra
$\mathbf {T}(V)$
is a system of generators of the finite B-algebra
![]() $\mathbf {T}(V)$
. We denote by
$\mathbf {T}(V)$
. We denote by
 $\mathbb {A}^{I}_{V_{L}}$
the affine space over
$\mathbb {A}^{I}_{V_{L}}$
the affine space over
![]() $V_{L}=V\hat {\otimes }_{K} L$
whose variables are indexed by I. We have a morphism of rigid analytic varieties
$V_{L}=V\hat {\otimes }_{K} L$
whose variables are indexed by I. We have a morphism of rigid analytic varieties
 $$ \begin{align*} i_{V,I}: \mathcal{E}(V)_{L}\to \mathbb{A}^{I}_{V_{L}},\quad z\mapsto (h(z))_{h\in I}. \end{align*} $$
$$ \begin{align*} i_{V,I}: \mathcal{E}(V)_{L}\to \mathbb{A}^{I}_{V_{L}},\quad z\mapsto (h(z))_{h\in I}. \end{align*} $$
From the definition of I, we see that the map
![]() $i_{V,I}$
is a closed immersion.
$i_{V,I}$
is a closed immersion.
On the other hand, we also have a morphism of rigid analytic varieties
 $$ \begin{align*} \mu: X\to \mathrm{Sp}(R_{L})\times \mathbb{A}_{L}^{1}, \quad x\mapsto \left(\kappa(x),\varphi(\phi)^{-1}(x)\right). \end{align*} $$
$$ \begin{align*} \mu: X\to \mathrm{Sp}(R_{L})\times \mathbb{A}_{L}^{1}, \quad x\mapsto \left(\kappa(x),\varphi(\phi)^{-1}(x)\right). \end{align*} $$
Let
![]() $P(T)\in R\{\{T\}\}$
be the characteristic power series of
$P(T)\in R\{\{T\}\}$
be the characteristic power series of
![]() $\phi $
acting on M. For any
$\phi $
acting on M. For any
![]() $x\in X$
, let
$x\in X$
, let
![]() $P_{x}(T)$
be the image of
$P_{x}(T)$
be the image of
![]() $P(T)$
in
$P(T)$
in
![]() $k(x)\{\{T\}\}$
by the map
$k(x)\{\{T\}\}$
by the map
![]() $\kappa ^{*}(x): R\to k(x)$
. By [Reference Buzzard12, Lemma 2.13], it is the characteristic power series of
$\kappa ^{*}(x): R\to k(x)$
. By [Reference Buzzard12, Lemma 2.13], it is the characteristic power series of
![]() $\phi $
acting on
$\phi $
acting on
 $M\hat {\otimes }_{R,\kappa ^{*}(x)} k(x)$
. By assumption, there exists a nonzero element
$M\hat {\otimes }_{R,\kappa ^{*}(x)} k(x)$
. By assumption, there exists a nonzero element
![]() $g_{x}$
of
$g_{x}$
of
 $M\hat {\otimes }_{R,\kappa ^{*}(x)} k(x)$
satisfying
$M\hat {\otimes }_{R,\kappa ^{*}(x)} k(x)$
satisfying
Then Lemma 2.1(3) implies
 $P_{x}\left (\varphi (\phi )(x)^{-1}\right )=0$
. Using the assumption that X is reduced and Lemma 2.6(1), we see that the morphism
$P_{x}\left (\varphi (\phi )(x)^{-1}\right )=0$
. Using the assumption that X is reduced and Lemma 2.6(1), we see that the morphism
![]() $\mu $
factors through
$\mu $
factors through
![]() $Z_{\phi ,L}$
.
$Z_{\phi ,L}$
.
For any
![]() $V\in \mathcal {C}$
, put
$V\in \mathcal {C}$
, put
![]() $X_{V_{L}}=\mu ^{-1}(V_{L})$
. For any I as before, we consider the morphism of rigid analytic varieties over
$X_{V_{L}}=\mu ^{-1}(V_{L})$
. For any I as before, we consider the morphism of rigid analytic varieties over
![]() $V_{L}$
$V_{L}$
 $$ \begin{align*} j_{V,I}: X_{V_{L}} \to \mathbb{A}^{I}_{V_{L}},\quad x\mapsto (\varphi(h)(x))_{h\in I}. \end{align*} $$
$$ \begin{align*} j_{V,I}: X_{V_{L}} \to \mathbb{A}^{I}_{V_{L}},\quad x\mapsto (\varphi(h)(x))_{h\in I}. \end{align*} $$
By [Reference Buzzard12, Lemma 5.9] and Lemma 2.1(1), for any
![]() $x\in X_{V_{L}}$
there exists a unique point
$x\in X_{V_{L}}$
there exists a unique point
![]() $z_{x}\in \mathcal {E}(k(x))$
satisfying
$z_{x}\in \mathcal {E}(k(x))$
satisfying
![]() $\varphi (h)(x)=h(z_{x})$
for any
$\varphi (h)(x)=h(z_{x})$
for any
![]() $h\in \mathbf {T}$
. We claim that
$h\in \mathbf {T}$
. We claim that
![]() $z_{x}\in \mathcal {E}(V)_{L}$
. Indeed, we may assume that
$z_{x}\in \mathcal {E}(V)_{L}$
. Indeed, we may assume that
![]() $f(V)$
is connected. Let
$f(V)$
is connected. Let
![]() $Q(T)$
be the factor of
$Q(T)$
be the factor of
![]() $P(T)$
corresponding to V and let
$P(T)$
corresponding to V and let
![]() $Q_{x}(T)$
be its image by
$Q_{x}(T)$
be its image by
![]() $\kappa ^{*}(x)$
. Let N be the direct summand of
$\kappa ^{*}(x)$
. Let N be the direct summand of
![]() $M_{A}$
corresponding to V. For any
$M_{A}$
corresponding to V. For any
![]() $x\in X_{V_{L}}$
, we have
$x\in X_{V_{L}}$
, we have
![]() $\mu (x)\in V_{L}$
and
$\mu (x)\in V_{L}$
and
 $Q_{x}\left (\varphi \left (\phi ^{-1}\right ) (x)\right )=Q^{*}_{x}(\varphi (\phi )(x))=0$
. Hence
$Q_{x}\left (\varphi \left (\phi ^{-1}\right ) (x)\right )=Q^{*}_{x}(\varphi (\phi )(x))=0$
. Hence
![]() $Q^{*}_{x}(\phi )g_{x}=0$
and thus
$Q^{*}_{x}(\phi )g_{x}=0$
and thus
![]() $g_{x}\in N\otimes _{A} k(x)$
. From the proof of [Reference Buzzard12, Lemma 5.9], this implies
$g_{x}\in N\otimes _{A} k(x)$
. From the proof of [Reference Buzzard12, Lemma 5.9], this implies
![]() $z_{x}\in \mathcal {E}(V)_{L}$
, and the claim follows.
$z_{x}\in \mathcal {E}(V)_{L}$
, and the claim follows.
In particular, we have
![]() $j_{V,I}(x)=i_{V,I}(z_{x})$
for any
$j_{V,I}(x)=i_{V,I}(z_{x})$
for any
![]() $x\in X_{V_{L}}$
and thus
$x\in X_{V_{L}}$
and thus
![]() $j_{V,I}\left (X_{V_{L}}\right )\subseteq i_{V,I}(\mathcal {E}(V)_{L})$
. Since
$j_{V,I}\left (X_{V_{L}}\right )\subseteq i_{V,I}(\mathcal {E}(V)_{L})$
. Since
![]() $i_{V,I}$
is a closed immersion and
$i_{V,I}$
is a closed immersion and
![]() $X_{V_{L}}$
is reduced, Lemma 2.6(1) yields a unique morphism
$X_{V_{L}}$
is reduced, Lemma 2.6(1) yields a unique morphism
![]() $\Phi _{V,I}: X_{V_{L}}\to \mathcal {E}(V)_{L}$
over
$\Phi _{V,I}: X_{V_{L}}\to \mathcal {E}(V)_{L}$
over
![]() $V_{L}$
which makes the following diagram commutative:
$V_{L}$
which makes the following diagram commutative:

We claim that the morphism
![]() $\Phi _{V,I}$
is independent of the choice of a finite subset I of
$\Phi _{V,I}$
is independent of the choice of a finite subset I of
![]() $\mathbf {T}$
as before. Indeed, for any
$\mathbf {T}$
as before. Indeed, for any
![]() $x\in X_{V_{L}}$
, we have
$x\in X_{V_{L}}$
, we have
 $\Phi _{V,I}(x)=i_{V,I}^{-1}\left (j_{V,I}(x)\right )=z_{x}$
, which depends only on x. Since X is reduced and
$\Phi _{V,I}(x)=i_{V,I}^{-1}\left (j_{V,I}(x)\right )=z_{x}$
, which depends only on x. Since X is reduced and
![]() $\mathcal {E}$
is separated, Lemma 2.6(2) implies the claim. Moreover, for the same reason we can glue the morphisms
$\mathcal {E}$
is separated, Lemma 2.6(2) implies the claim. Moreover, for the same reason we can glue the morphisms
![]() $\Phi _{V,I}$
along
$\Phi _{V,I}$
along
![]() $V\in \mathcal {C}$
and obtain a morphism
$V\in \mathcal {C}$
and obtain a morphism
![]() $\Phi : X\to \mathcal {E}_{L}$
. Since the requirement on
$\Phi : X\to \mathcal {E}_{L}$
. Since the requirement on
![]() $\Phi $
in the proposition is the same as
$\Phi $
in the proposition is the same as
![]() $\Phi (x)=z_{x}$
, it is satisfied by the morphism
$\Phi (x)=z_{x}$
, it is satisfied by the morphism
![]() $\Phi $
we have constructed. Lemma 2.6(2) ensures uniqueness.
$\Phi $
we have constructed. Lemma 2.6(2) ensures uniqueness.
3 Hilbert eigenvariety
3.1 Hilbert modular varieties
Let p be a rational prime. Let F be a totally real number field of degree g which is unramified over p. We denote its ring of integers by
![]() $\mathfrak {o}=\mathcal {O}_{F}$
and its different by
$\mathfrak {o}=\mathcal {O}_{F}$
and its different by
![]() $\mathcal {D}_{F}$
. For any integer N, we put
$\mathcal {D}_{F}$
. For any integer N, we put
 $$ \begin{align*} U_{N}=\left\{\epsilon\in \mathcal{O}_{F}^{\times}\mid \epsilon\equiv 1 \bmod N\right\}. \end{align*} $$
$$ \begin{align*} U_{N}=\left\{\epsilon\in \mathcal{O}_{F}^{\times}\mid \epsilon\equiv 1 \bmod N\right\}. \end{align*} $$
For any prime ideal
![]() $\mathfrak {p} \mid p$
of
$\mathfrak {p} \mid p$
of
![]() $\mathcal {O}_{F}$
, let
$\mathcal {O}_{F}$
, let
![]() $f_{\mathfrak {p}}$
be the residue degree of
$f_{\mathfrak {p}}$
be the residue degree of
![]() $\mathfrak {p}$
.
$\mathfrak {p}$
.
Fix a finite extension
![]() $K/\mathbb {Q}_{p}$
in
$K/\mathbb {Q}_{p}$
in
![]() $\bar {\mathbb {Q}}_{p}$
such that
$\bar {\mathbb {Q}}_{p}$
such that
![]() $F\otimes K$
splits completely. We denote by
$F\otimes K$
splits completely. We denote by
![]() $\mathcal {O}_{K}$
the ring of integers of K, by
$\mathcal {O}_{K}$
the ring of integers of K, by
![]() $m_{K}$
the maximal ideal of
$m_{K}$
the maximal ideal of
![]() $\mathcal {O}_{K}$
, by
$\mathcal {O}_{K}$
, by
![]() $\pi _{K}$
a uniformizer of K, by e the absolute ramification index of K, by k the residue field of K, and by
$\pi _{K}$
a uniformizer of K, by e the absolute ramification index of K, by k the residue field of K, and by
![]() $W=W(k)$
the Witt ring of k. Let
$W=W(k)$
the Witt ring of k. Let
![]() $v_{p}$
be the additive valuation on K normalized as
$v_{p}$
be the additive valuation on K normalized as
![]() $v_{p}(p)=1$
. For any nonnegative real number i, we put
$v_{p}(p)=1$
. For any nonnegative real number i, we put
 $$ \begin{align*} m_{K}^{\geqslant i}=\left\{x\in \mathcal{O}_{K}\mid v_{p}(x)\geq i\right\}, \qquad \mathcal{O}_{K,i}=\mathcal{O}_{K}/m_{K}^{\geqslant i},\qquad \mathscr{S}_{i}=\mathrm{Spec}\left(\mathcal{O}_{K,i}\right). \end{align*} $$
$$ \begin{align*} m_{K}^{\geqslant i}=\left\{x\in \mathcal{O}_{K}\mid v_{p}(x)\geq i\right\}, \qquad \mathcal{O}_{K,i}=\mathcal{O}_{K}/m_{K}^{\geqslant i},\qquad \mathscr{S}_{i}=\mathrm{Spec}\left(\mathcal{O}_{K,i}\right). \end{align*} $$
For any extension
![]() $L/K$
of valuation fields, we consider the valuation on L extending
$L/K$
of valuation fields, we consider the valuation on L extending
![]() $v_{p}$
and define
$v_{p}$
and define
![]() $\mathcal {O}_{L}$
,
$\mathcal {O}_{L}$
,
![]() $m_{L}$
,
$m_{L}$
,
 $m_{L}^{\geqslant i}$
,
$m_{L}^{\geqslant i}$
,
![]() $\mathcal {O}_{L,i}$
, and
$\mathcal {O}_{L,i}$
, and
![]() $\mathscr {S}_{L,i}=\mathrm {Spec}(\mathcal {O}_{L,i})$
similarly. For any element
$\mathscr {S}_{L,i}=\mathrm {Spec}(\mathcal {O}_{L,i})$
similarly. For any element
![]() $x\in \mathcal {O}_{L,1}$
, we define the truncated valuation
$x\in \mathcal {O}_{L,1}$
, we define the truncated valuation
![]() $v_{p}(x)$
by
$v_{p}(x)$
by
with any lift
![]() $\hat {x}\in \mathcal {O}_{L}$
of x. For any
$\hat {x}\in \mathcal {O}_{L}$
of x. For any
![]() $x\in L$
, we define the absolute value of x by
$x\in L$
, we define the absolute value of x by
![]() $\lvert x\rvert =p^{-v_{p}(x)}$
.
$\lvert x\rvert =p^{-v_{p}(x)}$
.
We denote by
![]() $\mathbb {B}_{F}$
the set of embeddings
$\mathbb {B}_{F}$
the set of embeddings
![]() $F\to K$
and by
$F\to K$
and by
![]() $\mathbb {B}_{\mathfrak {p}}$
the subset of
$\mathbb {B}_{\mathfrak {p}}$
the subset of
![]() $\mathbb {B}_{F}$
consisting of embeddings which factor through the completion
$\mathbb {B}_{F}$
consisting of embeddings which factor through the completion
![]() $F_{\mathfrak {p}}$
. The set
$F_{\mathfrak {p}}$
. The set
![]() $\mathbb {B}_{F}$
is decomposed as
$\mathbb {B}_{F}$
is decomposed as
 $$ \begin{align*} \mathbb{B}_{F}=\coprod_{\mathfrak{p}\mid p} \mathbb{B}_{\mathfrak{p}}. \end{align*} $$
$$ \begin{align*} \mathbb{B}_{F}=\coprod_{\mathfrak{p}\mid p} \mathbb{B}_{\mathfrak{p}}. \end{align*} $$
For any subset X of F, we denote by
![]() $X^{+}$
the subset of totally positive elements of X. Put
$X^{+}$
the subset of totally positive elements of X. Put
![]() $F_{\mathbb {R}}=F\otimes \mathbb {R}$
and
$F_{\mathbb {R}}=F\otimes \mathbb {R}$
and
![]() $F^{*}_{\mathbb {R}}=\mathrm {Hom}_{\mathbb {Q}}(F,\mathbb {R})$
. We denote by
$F^{*}_{\mathbb {R}}=\mathrm {Hom}_{\mathbb {Q}}(F,\mathbb {R})$
. We denote by
 $F^{*,+}_{\mathbb {R}}$
the subset of
$F^{*,+}_{\mathbb {R}}$
the subset of
![]() $F^{*}_{\mathbb {R}}$
consisting of linear forms which maps the subset
$F^{*}_{\mathbb {R}}$
consisting of linear forms which maps the subset
![]() $F^{\times ,+}$
to
$F^{\times ,+}$
to
![]() $\mathbb {R}_{>0}$
. The group
$\mathbb {R}_{>0}$
. The group
![]() $U_{N}$
acts on F and
$U_{N}$
acts on F and
 $F^{*,+}_{\mathbb {R}}$
through
$F^{*,+}_{\mathbb {R}}$
through
![]() $\epsilon \mapsto \epsilon ^{2}$
.
$\epsilon \mapsto \epsilon ^{2}$
.
Let
![]() $\mathfrak {c}$
be any nonzero fractional ideal of F. For any fractional ideals
$\mathfrak {c}$
be any nonzero fractional ideal of F. For any fractional ideals
![]() $\mathfrak {a}, \mathfrak {b}$
of F satisfying
$\mathfrak {a}, \mathfrak {b}$
of F satisfying
![]() $\mathfrak {a}\mathfrak {b}^{-1}=\mathfrak {c}$
, we denote by
$\mathfrak {a}\mathfrak {b}^{-1}=\mathfrak {c}$
, we denote by
![]() $\mathrm {Dec}(\mathfrak {a},\mathfrak {b})$
the set of rational polyhedral cone decompositions
$\mathrm {Dec}(\mathfrak {a},\mathfrak {b})$
the set of rational polyhedral cone decompositions
![]() $\mathscr {C}=\{\sigma \}_{\sigma \in \mathscr {C}}$
of
$\mathscr {C}=\{\sigma \}_{\sigma \in \mathscr {C}}$
of
 $F^{*,+}_{\mathbb {R}}$
which is projective and smooth with respect to the lattice
$F^{*,+}_{\mathbb {R}}$
which is projective and smooth with respect to the lattice
![]() $\mathrm {Hom}(\mathfrak {a}\mathfrak {b},\mathbb {Z})$
such that the elements of
$\mathrm {Hom}(\mathfrak {a}\mathfrak {b},\mathbb {Z})$
such that the elements of
![]() $\mathscr {C}$
are permuted by the action of
$\mathscr {C}$
are permuted by the action of
![]() $U_{N}$
, the set
$U_{N}$
, the set
![]() $\mathscr {C}/U_{N}$
is finite, and for any
$\mathscr {C}/U_{N}$
is finite, and for any
![]() $\epsilon \in U_{N}$
and
$\epsilon \in U_{N}$
and
![]() $\sigma \in \mathscr {C}$
,
$\sigma \in \mathscr {C}$
,
![]() $\epsilon (\sigma )\cap \sigma \neq \emptyset $
implies
$\epsilon (\sigma )\cap \sigma \neq \emptyset $
implies
![]() $\epsilon =1$
, as in [Reference Hida31, §4.1.4]. Here we adopt the convention that
$\epsilon =1$
, as in [Reference Hida31, §4.1.4]. Here we adopt the convention that
![]() $\sigma $
is an open cone. Note that any two elements of
$\sigma $
is an open cone. Note that any two elements of
![]() $\mathrm {Dec}(\mathfrak {a},\mathfrak {b})$
have a common refinement which belongs to
$\mathrm {Dec}(\mathfrak {a},\mathfrak {b})$
have a common refinement which belongs to
![]() $\mathrm {Dec}(\mathfrak {a},\mathfrak {b})$
. For any such pair
$\mathrm {Dec}(\mathfrak {a},\mathfrak {b})$
. For any such pair
![]() $(\mathfrak {a},\mathfrak {b})$
, we fix once and for all a rational polyhedral cone decomposition
$(\mathfrak {a},\mathfrak {b})$
, we fix once and for all a rational polyhedral cone decomposition
![]() $\mathscr {C}(\mathfrak {a},\mathfrak {b})\in \mathrm {Dec}(\mathfrak {a},\mathfrak {b})$
and put
$\mathscr {C}(\mathfrak {a},\mathfrak {b})\in \mathrm {Dec}(\mathfrak {a},\mathfrak {b})$
and put
 $\mathscr {D}(\mathfrak {c})=\left \{\mathscr {C}(\mathfrak {a},\mathfrak {b})\mid \mathfrak {a}\mathfrak {b}^{-1}=\mathfrak {c}\right \}$
.
$\mathscr {D}(\mathfrak {c})=\left \{\mathscr {C}(\mathfrak {a},\mathfrak {b})\mid \mathfrak {a}\mathfrak {b}^{-1}=\mathfrak {c}\right \}$
.
3.1.1 Hilbert–Blumenthal abelian varieties
Let
![]() $N\geq 4$
be an integer with
$N\geq 4$
be an integer with
![]() $p\nmid N$
and let
$p\nmid N$
and let
![]() $\mathfrak {c}$
be a nonzero fractional ideal of F. Let S be a scheme over
$\mathfrak {c}$
be a nonzero fractional ideal of F. Let S be a scheme over
![]() $\mathcal {O}_{K}$
. A Hilbert–Blumenthal abelian variety over S, which we abbreviate as ‘HBAV’, is a quadruple
$\mathcal {O}_{K}$
. A Hilbert–Blumenthal abelian variety over S, which we abbreviate as ‘HBAV’, is a quadruple
![]() $(A,\iota ,\lambda ,\psi )$
such that the following are true:
$(A,\iota ,\lambda ,\psi )$
such that the following are true:
-
• A is an abelian scheme over S of relative dimension g.
-
•
 $\iota : \mathcal {O}_{F}\to \mathrm {End}_{S}(A)$
is a ring homomorphism.
$\iota : \mathcal {O}_{F}\to \mathrm {End}_{S}(A)$
is a ring homomorphism. -
•
 $\lambda $
is a
$\lambda $
is a
 $\mathfrak {c}$
-polarization. Namely,
$\mathfrak {c}$
-polarization. Namely,
 $\lambda :A\otimes _{\mathcal {O}_{F}} \mathfrak {c}\simeq A^{\vee }$
is an isomorphism of abelian schemes to the dual abelian scheme
$\lambda :A\otimes _{\mathcal {O}_{F}} \mathfrak {c}\simeq A^{\vee }$
is an isomorphism of abelian schemes to the dual abelian scheme
 $A^{\vee }$
compatible with
$A^{\vee }$
compatible with
 $\mathcal {O}_{F}$
-action such that the map induces an isomorphism of
$\mathcal {O}_{F}$
-action such that the map induces an isomorphism of $$ \begin{align*} \mathrm{Hom}_{\mathcal{O}_{F}}\left(A,A^{\vee}\right)\simeq \mathrm{Hom}_{\mathcal{O}_{F}}\left(A,A\otimes_{\mathcal{O}_{F}} \mathfrak{c}\right),\quad f\mapsto \lambda^{-1}\circ f, \end{align*} $$
$$ \begin{align*} \mathrm{Hom}_{\mathcal{O}_{F}}\left(A,A^{\vee}\right)\simeq \mathrm{Hom}_{\mathcal{O}_{F}}\left(A,A\otimes_{\mathcal{O}_{F}} \mathfrak{c}\right),\quad f\mapsto \lambda^{-1}\circ f, \end{align*} $$
 $\mathcal {O}_{F}$
-modules with notion of positivity
$\mathcal {O}_{F}$
-modules with notion of positivity
 $\left (\mathcal {P}_{A},\mathcal {P}_{A}^{+}\right )\simeq \left (\mathfrak {c},\mathfrak {c}^{+}\right )$
. Here
$\left (\mathcal {P}_{A},\mathcal {P}_{A}^{+}\right )\simeq \left (\mathfrak {c},\mathfrak {c}^{+}\right )$
. Here
 $\mathcal {P}_{A}$
denotes the
$\mathcal {P}_{A}$
denotes the
 $\mathcal {O}_{F}$
-module of symmetric
$\mathcal {O}_{F}$
-module of symmetric
 $\mathcal {O}_{F}$
-homomorphisms from A to
$\mathcal {O}_{F}$
-homomorphisms from A to
 $A^{\vee }$
,
$A^{\vee }$
,
 $\mathcal {P}_{A}^{+}$
is the subset of
$\mathcal {P}_{A}^{+}$
is the subset of
 $\mathcal {O}_{F}$
-linear polarizations, and any element
$\mathcal {O}_{F}$
-linear polarizations, and any element
 $\gamma \in \mathfrak {c}$
is identified with the element
$\gamma \in \mathfrak {c}$
is identified with the element
 $(x\mapsto x\otimes \gamma )$
of
$(x\mapsto x\otimes \gamma )$
of
 $\mathrm {Hom}_{\mathcal {O}_{F}}\left (A,A\otimes _{\mathcal {O}_{F}} \mathfrak {c}\right )$
.
$\mathrm {Hom}_{\mathcal {O}_{F}}\left (A,A\otimes _{\mathcal {O}_{F}} \mathfrak {c}\right )$
.
-
•
 $\psi : \mathcal {D}_{F}^{-1}\otimes \mu _{N}\to A$
is an
$\psi : \mathcal {D}_{F}^{-1}\otimes \mu _{N}\to A$
is an
 $\mathcal {O}_{F}$
-linear closed immersion of group schemes, which we call a
$\mathcal {O}_{F}$
-linear closed immersion of group schemes, which we call a
 $\Gamma _{00}(N)$
-structure.
$\Gamma _{00}(N)$
-structure.
Note that for such data, the
![]() $\mathcal {O}_{F}\otimes \mathcal {O}_{S}$
-module
$\mathcal {O}_{F}\otimes \mathcal {O}_{S}$
-module
![]() $\mathrm {Lie}(A)$
is locally free of rank
$\mathrm {Lie}(A)$
is locally free of rank
![]() $1$
[Reference Deligne and Pappas20, Corollaire 2.9]. While the notion of an HBAV depends on
$1$
[Reference Deligne and Pappas20, Corollaire 2.9]. While the notion of an HBAV depends on
![]() $\mathfrak {c}$
, we will omit the reference to
$\mathfrak {c}$
, we will omit the reference to
![]() $\mathfrak {c}$
when there is no risk of confusion.
$\mathfrak {c}$
when there is no risk of confusion.
Let
![]() $L/K$
be an extension of complete valuation fields and let
$L/K$
be an extension of complete valuation fields and let
![]() $\mathfrak {p}$
be a prime ideal of
$\mathfrak {p}$
be a prime ideal of
![]() $\mathcal {O}_{F}$
dividing p. Let
$\mathcal {O}_{F}$
dividing p. Let
![]() $\mathcal {G}$
be a finite flat group scheme over
$\mathcal {G}$
be a finite flat group scheme over
![]() $ \mathcal {O}_{L}$
with an
$ \mathcal {O}_{L}$
with an
![]() $\mathcal {O}_{F_{\mathfrak {p}}}$
-action. We have decompositions
$\mathcal {O}_{F_{\mathfrak {p}}}$
-action. We have decompositions
 $$ \begin{align*} \omega_{\mathcal{G}}=\bigoplus_{\beta\in \mathbb{B}_{\mathfrak{p}}} \omega_{\mathcal{G},\beta},\qquad \mathrm{Lie}\left(\mathcal{G}\times \mathscr{S}_{L,n}\right)=\bigoplus_{\beta\in \mathbb{B}_{\mathfrak{p}}} \mathrm{Lie}\left(\mathcal{G}\times \mathscr{S}_{L,n}\right)_{\beta} \end{align*} $$
$$ \begin{align*} \omega_{\mathcal{G}}=\bigoplus_{\beta\in \mathbb{B}_{\mathfrak{p}}} \omega_{\mathcal{G},\beta},\qquad \mathrm{Lie}\left(\mathcal{G}\times \mathscr{S}_{L,n}\right)=\bigoplus_{\beta\in \mathbb{B}_{\mathfrak{p}}} \mathrm{Lie}\left(\mathcal{G}\times \mathscr{S}_{L,n}\right)_{\beta} \end{align*} $$
according with the decomposition
 $\mathcal {O}_{F_{\mathfrak {p}}}\otimes W\simeq \prod _{\beta \in \mathbb {B}_{\mathfrak {p}}} W$
. Write
$\mathcal {O}_{F_{\mathfrak {p}}}\otimes W\simeq \prod _{\beta \in \mathbb {B}_{\mathfrak {p}}} W$
. Write
![]() $\omega _{\mathcal {G},\beta }\simeq \bigoplus _{i} \mathcal {O}_{L}/(a_{i})$
with some
$\omega _{\mathcal {G},\beta }\simeq \bigoplus _{i} \mathcal {O}_{L}/(a_{i})$
with some
![]() $a_{i}\in \mathcal {O}_{L}$
, and define the
$a_{i}\in \mathcal {O}_{L}$
, and define the
![]() $\beta $
-degree of
$\beta $
-degree of
![]() $\mathcal {G}$
by
$\mathcal {G}$
by
![]() $\deg _{\beta }(\mathcal {G})=\sum _{i} v_{p}(a_{i})$
. Similarly, for any finite flat group scheme
$\deg _{\beta }(\mathcal {G})=\sum _{i} v_{p}(a_{i})$
. Similarly, for any finite flat group scheme
![]() $\mathcal {H}$
over
$\mathcal {H}$
over
![]() $\mathcal {O}_{L}$
with an
$\mathcal {O}_{L}$
with an
![]() $\mathcal {O}_{F}$
-action, we have decompositions
$\mathcal {O}_{F}$
-action, we have decompositions
 $$ \begin{align*} \mathcal{H}=\bigoplus_{\mathfrak{p}\mid p} \mathcal{H}_{\mathfrak{p}},\qquad \omega_{\mathcal{H}}=\bigoplus_{\beta\in \mathbb{B}_{F}} \omega_{\mathcal{H},\beta} \end{align*} $$
$$ \begin{align*} \mathcal{H}=\bigoplus_{\mathfrak{p}\mid p} \mathcal{H}_{\mathfrak{p}},\qquad \omega_{\mathcal{H}}=\bigoplus_{\beta\in \mathbb{B}_{F}} \omega_{\mathcal{H},\beta} \end{align*} $$
such that
![]() $\mathcal {H}_{\mathfrak {p}}$
is a finite flat closed subgroup scheme of
$\mathcal {H}_{\mathfrak {p}}$
is a finite flat closed subgroup scheme of
![]() $\mathcal {H}$
over
$\mathcal {H}$
over
![]() $\mathcal {O}_{L}$
and
$\mathcal {O}_{L}$
and
![]() $\omega _{\mathcal {H},\beta }=\omega _{\mathcal {H}_{\mathfrak {p}},\beta }$
for any
$\omega _{\mathcal {H},\beta }=\omega _{\mathcal {H}_{\mathfrak {p}},\beta }$
for any
![]() $\beta \in \mathbb {B}_{\mathfrak {p}}$
. We put
$\beta \in \mathbb {B}_{\mathfrak {p}}$
. We put
![]() $\deg _{\beta }(\mathcal {H})=\deg _{\beta }\left (\mathcal {H}_{\mathfrak {p}}\right )$
for any
$\deg _{\beta }(\mathcal {H})=\deg _{\beta }\left (\mathcal {H}_{\mathfrak {p}}\right )$
for any
![]() $\beta \in \mathbb {B}_{\mathfrak {p}}$
.
$\beta \in \mathbb {B}_{\mathfrak {p}}$
.
Suppose that
![]() $\mathcal {G}$
is a truncated Barsotti–Tate group of level n, height h, and dimension d over
$\mathcal {G}$
is a truncated Barsotti–Tate group of level n, height h, and dimension d over
![]() $\mathcal {O}_{L}$
. For the p-torsion part
$\mathcal {O}_{L}$
. For the p-torsion part
![]() $\mathcal {G}[p]$
of
$\mathcal {G}[p]$
of
![]() $\mathcal {G}$
, the Lie algebra
$\mathcal {G}$
, the Lie algebra
![]() $\mathrm {Lie}\left (\mathcal {G}^{\vee }[p] \times \mathscr {S}_{L,1}\right )$
is a free
$\mathrm {Lie}\left (\mathcal {G}^{\vee }[p] \times \mathscr {S}_{L,1}\right )$
is a free
![]() $\mathcal {O}_{L,1}$
-module of rank
$\mathcal {O}_{L,1}$
-module of rank
![]() $h-d$
. The Verschiebung of
$h-d$
. The Verschiebung of
![]() $\mathcal {G}^{\vee }[p]\times \mathscr {S}_{L,1}$
yields a map
$\mathcal {G}^{\vee }[p]\times \mathscr {S}_{L,1}$
yields a map
 $$ \begin{align*} \mathrm{Lie}\left(V_{\mathcal{G}^{\vee}[p]\times \mathscr{S}_{L,1}}\right): \mathrm{Lie}\left(\mathcal{G}^{\vee}[p]\times \mathscr{S}_{L,1}\right)^{(p)} \to \mathrm{Lie}\left(\mathcal{G}^{\vee}[p]\times \mathscr{S}_{L,1}\right). \end{align*} $$
$$ \begin{align*} \mathrm{Lie}\left(V_{\mathcal{G}^{\vee}[p]\times \mathscr{S}_{L,1}}\right): \mathrm{Lie}\left(\mathcal{G}^{\vee}[p]\times \mathscr{S}_{L,1}\right)^{(p)} \to \mathrm{Lie}\left(\mathcal{G}^{\vee}[p]\times \mathscr{S}_{L,1}\right). \end{align*} $$
Then the Hodge height
![]() $\mathrm {Hdg}(\mathcal {G})$
of
$\mathrm {Hdg}(\mathcal {G})$
of
![]() $\mathcal {G}$
is by definition the truncated valuation for
$\mathcal {G}$
is by definition the truncated valuation for
![]() $v_{p}$
of the determinant of a representing matrix of this map. Moreover, if the ring
$v_{p}$
of the determinant of a representing matrix of this map. Moreover, if the ring
![]() $\mathcal {O}_{F_{\mathfrak {p}}}$
acts on
$\mathcal {O}_{F_{\mathfrak {p}}}$
acts on
![]() $\mathcal {G}$
, then this map is also decomposed as the direct sum of maps
$\mathcal {G}$
, then this map is also decomposed as the direct sum of maps
 $$ \begin{align*} \mathrm{Lie}\left(V_{\mathcal{G}^{\vee}[p]\times\mathscr{S}_{L,1}}\right)_{\beta}: \mathrm{Lie}\left(\mathcal{G}^{\vee}[p]\times\mathscr{S}_{L,1}\right)_{\sigma^{-1}\circ\beta}\to \mathrm{Lie}\left(\mathcal{G}^{\vee}[p]\times\mathscr{S}_{L,1}\right)_{\beta}, \end{align*} $$
$$ \begin{align*} \mathrm{Lie}\left(V_{\mathcal{G}^{\vee}[p]\times\mathscr{S}_{L,1}}\right)_{\beta}: \mathrm{Lie}\left(\mathcal{G}^{\vee}[p]\times\mathscr{S}_{L,1}\right)_{\sigma^{-1}\circ\beta}\to \mathrm{Lie}\left(\mathcal{G}^{\vee}[p]\times\mathscr{S}_{L,1}\right)_{\beta}, \end{align*} $$
where
![]() $\sigma $
denotes the natural lift to W of the pth-power Frobenius map on k. If the
$\sigma $
denotes the natural lift to W of the pth-power Frobenius map on k. If the
![]() $\mathcal {O}_{L,1}$
-module
$\mathcal {O}_{L,1}$
-module
 $\mathrm {Lie}\left (\mathcal {G}^{\vee }[p]\times \mathscr {S}_{L,1}\right )_{\beta }$
is free for any
$\mathrm {Lie}\left (\mathcal {G}^{\vee }[p]\times \mathscr {S}_{L,1}\right )_{\beta }$
is free for any
![]() $\beta \in \mathbb {B}_{\mathfrak {p}}$
, we define the
$\beta \in \mathbb {B}_{\mathfrak {p}}$
, we define the
![]() $\beta $
-Hodge height
$\beta $
-Hodge height
![]() $\mathrm {Hdg}_{\beta }(\mathcal {G})$
of
$\mathrm {Hdg}_{\beta }(\mathcal {G})$
of
![]() $\mathcal {G}$
as the truncated valuation of the determinant of the map
$\mathcal {G}$
as the truncated valuation of the determinant of the map
 $ \mathrm {Lie}\left (V_{\mathcal {G}^{\vee }[p]\times \mathscr {S}_{L,1}}\right )_{\beta }$
. These assumptions are satisfied when
$ \mathrm {Lie}\left (V_{\mathcal {G}^{\vee }[p]\times \mathscr {S}_{L,1}}\right )_{\beta }$
. These assumptions are satisfied when
![]() $\mathcal {G}$
is the
$\mathcal {G}$
is the
![]() $\mathfrak {p}^{n}$
-torsion part
$\mathfrak {p}^{n}$
-torsion part
![]() $A[\mathfrak {p}^{n}]=A[p^{n}]_{\mathfrak {p}}$
of an HBAV A over
$A[\mathfrak {p}^{n}]=A[p^{n}]_{\mathfrak {p}}$
of an HBAV A over
![]() $\mathcal {O}_{L}$
or, more generally, when
$\mathcal {O}_{L}$
or, more generally, when
![]() $\mathcal {G}$
is an
$\mathcal {G}$
is an
![]() $\mathcal {O}_{F_{\mathfrak {p}}}$
-
$\mathcal {O}_{F_{\mathfrak {p}}}$
-
![]() $\mathrm {ADBT}_{n}$
[Reference Hattori29, §3]. For any
$\mathrm {ADBT}_{n}$
[Reference Hattori29, §3]. For any
![]() $\beta \in \mathbb {B}_{\mathfrak {p}}$
, we put
$\beta \in \mathbb {B}_{\mathfrak {p}}$
, we put
![]() $ \mathrm {Hdg}_{\beta }(A)=\mathrm {Hdg}_{\beta }(A[\mathfrak {p}^{n}])$
.
$ \mathrm {Hdg}_{\beta }(A)=\mathrm {Hdg}_{\beta }(A[\mathfrak {p}^{n}])$
.
3.1.2 Moduli spaces and toroidal compactifications
Let
![]() $M(\mu _{N},\mathfrak {c})$
be the Hilbert modular variety over
$M(\mu _{N},\mathfrak {c})$
be the Hilbert modular variety over
![]() $\mathcal {O}_{K}$
which parametrizes the isomorphism classes of HBAVs
$\mathcal {O}_{K}$
which parametrizes the isomorphism classes of HBAVs
![]() $(A,\iota , \lambda , \psi )$
such that
$(A,\iota , \lambda , \psi )$
such that
![]() $ \lambda $
is a
$ \lambda $
is a
![]() $\mathfrak {c}$
-polarization and
$\mathfrak {c}$
-polarization and
![]() $\psi $
is a
$\psi $
is a
![]() $\Gamma _{00}(N)$
-structure. The scheme
$\Gamma _{00}(N)$
-structure. The scheme
![]() $M(\mu _{N},\mathfrak {c})$
is smooth over
$M(\mu _{N},\mathfrak {c})$
is smooth over
![]() $\mathcal {O}_{K}$
[Reference Goren26, Chapter 3, Theorem 6.9]. We denote by
$\mathcal {O}_{K}$
[Reference Goren26, Chapter 3, Theorem 6.9]. We denote by
![]() $A^{\mathrm {un}}$
the universal HBAV over
$A^{\mathrm {un}}$
the universal HBAV over
![]() $M(\mu _{N},\mathfrak {c})$
.
$M(\mu _{N},\mathfrak {c})$
.
An unramified cusp for
![]() $M(\mu _{N},\mathfrak {c})$
is a triple
$M(\mu _{N},\mathfrak {c})$
is a triple
![]() $(\mathfrak {a},\mathfrak {b}, \phi _{N})$
of fractional ideals
$(\mathfrak {a},\mathfrak {b}, \phi _{N})$
of fractional ideals
![]() $\mathfrak {a},\mathfrak {b}$
of F satisfying
$\mathfrak {a},\mathfrak {b}$
of F satisfying
![]() $\mathfrak {a}\mathfrak {b}^{-1}=\mathfrak {c}$
and an isomorphism of
$\mathfrak {a}\mathfrak {b}^{-1}=\mathfrak {c}$
and an isomorphism of
![]() $\mathcal {O}_{F}$
-modules
$\mathcal {O}_{F}$
-modules
For each cusp, we have a Tate object
![]() $\mathrm {Tate}_{\mathfrak {a},\mathfrak {b}}(q)$
over a certain base scheme [Reference Rapoport36, §4], which is used to construct a toroidal compactification
$\mathrm {Tate}_{\mathfrak {a},\mathfrak {b}}(q)$
over a certain base scheme [Reference Rapoport36, §4], which is used to construct a toroidal compactification
![]() $\bar {M}(\mu _{N},\mathfrak {c})$
of
$\bar {M}(\mu _{N},\mathfrak {c})$
of
![]() $M(\mu _{N},\mathfrak {c})$
. We recall the definition for unramified cusps. Put
$M(\mu _{N},\mathfrak {c})$
. We recall the definition for unramified cusps. Put
![]() $M=\mathfrak {a} \mathfrak {b}$
,
$M=\mathfrak {a} \mathfrak {b}$
,
![]() $M_{\mathbb {R}}=M\otimes \mathbb {R}$
, and
$M_{\mathbb {R}}=M\otimes \mathbb {R}$
, and
![]() $M^{*}_{\mathbb {R}}=\mathrm {Hom}(M,\mathbb {R})$
. We identify
$M^{*}_{\mathbb {R}}=\mathrm {Hom}(M,\mathbb {R})$
. We identify
![]() $M\otimes \mathbb {Q}$
with F. Then any
$M\otimes \mathbb {Q}$
with F. Then any
![]() $\mathscr {C}\in \mathrm {Dec}(\mathfrak {a},\mathfrak {b})$
gives a rational polyhedral cone decomposition of
$\mathscr {C}\in \mathrm {Dec}(\mathfrak {a},\mathfrak {b})$
gives a rational polyhedral cone decomposition of
 $$ \begin{align*} M^{*,+}_{\mathbb{R}}=\left\{f\in M^{*}_{\mathbb{R}}\mid f(M^{+})\subseteq \mathbb{R}_{>0}\right\}. \end{align*} $$
$$ \begin{align*} M^{*,+}_{\mathbb{R}}=\left\{f\in M^{*}_{\mathbb{R}}\mid f(M^{+})\subseteq \mathbb{R}_{>0}\right\}. \end{align*} $$
For each
![]() $\sigma \in \mathscr {C}$
, put
$\sigma \in \mathscr {C}$
, put
Then we have an affine torus embedding
The affine schemes
![]() $\{S_{\sigma }\}_{\sigma \in \mathscr {C}}$
can be glued via
$\{S_{\sigma }\}_{\sigma \in \mathscr {C}}$
can be glued via
![]() $S_{\sigma }\cap S_{\tau }=S_{\sigma \cap \tau }$
to define a torus embedding
$S_{\sigma }\cap S_{\tau }=S_{\sigma \cap \tau }$
to define a torus embedding
![]() $S \to S_{\mathscr {C}}$
. We denote by
$S \to S_{\mathscr {C}}$
. We denote by
![]() $S^{\infty }_{\sigma }$
and
$S^{\infty }_{\sigma }$
and
![]() $S^{\infty }_{\mathscr {C}}=\bigcup _{\sigma \in \mathscr {C}} S^{\infty }_{\sigma }$
the complements of S in these embeddings with reduced structures. The formal completions along these closed subschemes are denoted by
$S^{\infty }_{\mathscr {C}}=\bigcup _{\sigma \in \mathscr {C}} S^{\infty }_{\sigma }$
the complements of S in these embeddings with reduced structures. The formal completions along these closed subschemes are denoted by
 $\hat {S}_{\sigma }=\mathrm {Spf}\left (\hat {R}_{\sigma }\right )$
and
$\hat {S}_{\sigma }=\mathrm {Spf}\left (\hat {R}_{\sigma }\right )$
and
![]() $\hat {S}_{\mathscr {C}}$
. By assumption, we can construct the quotient
$\hat {S}_{\mathscr {C}}$
. By assumption, we can construct the quotient
 $\hat {S}_{\mathscr {C}}/U_{N}$
by regluing
$\hat {S}_{\mathscr {C}}/U_{N}$
by regluing
 $\left \{\hat {S}_{\sigma }\right \}_{\sigma \in \mathscr {C}}$
via the action
$\left \{\hat {S}_{\sigma }\right \}_{\sigma \in \mathscr {C}}$
via the action
![]() $\epsilon : \hat {S}_{\sigma }\simeq \hat {S}_{\epsilon \sigma }$
for any
$\epsilon : \hat {S}_{\sigma }\simeq \hat {S}_{\epsilon \sigma }$
for any
![]() $\epsilon \in U_{N}$
. The closed subscheme
$\epsilon \in U_{N}$
. The closed subscheme
![]() $S^{\infty }_{\sigma }$
is defined by a principal ideal
$S^{\infty }_{\sigma }$
is defined by a principal ideal
![]() $\hat {I}_{\sigma }$
of the ring
$\hat {I}_{\sigma }$
of the ring
![]() $\hat {R}_{\sigma }$
satisfying
$\hat {R}_{\sigma }$
satisfying
 $\sqrt {\hat {I}_{\sigma }}=\hat {I}_{\sigma }$
. The ring
$\sqrt {\hat {I}_{\sigma }}=\hat {I}_{\sigma }$
. The ring
![]() $\hat {R}_{\sigma }$
is a Noetherian normal excellent ring which is complete with respect to the
$\hat {R}_{\sigma }$
is a Noetherian normal excellent ring which is complete with respect to the
![]() $\hat {I}_{\sigma }$
-adic topology. Put
$\hat {I}_{\sigma }$
-adic topology. Put
 $\bar {S}_{\sigma }=\mathrm {Spec}\left (\hat {R}_{\sigma }\right )$
,
$\bar {S}_{\sigma }=\mathrm {Spec}\left (\hat {R}_{\sigma }\right )$
,
 $\bar {S}_{\sigma }^{\infty }=V\left (\hat {I}_{\sigma }\right )$
, and
$\bar {S}_{\sigma }^{\infty }=V\left (\hat {I}_{\sigma }\right )$
, and
![]() $\bar {S}^{0}_{\sigma }=\bar {S}_{\sigma }\setminus \bar {S}_{\sigma }^{\infty }$
, where the latter is an affine scheme and we denote its affine ring by
$\bar {S}^{0}_{\sigma }=\bar {S}_{\sigma }\setminus \bar {S}_{\sigma }^{\infty }$
, where the latter is an affine scheme and we denote its affine ring by
![]() $\hat {R}_{\sigma }^{0}$
.
$\hat {R}_{\sigma }^{0}$
.
Note that the torus with character group
![]() $\mathfrak {a}$
is
$\mathfrak {a}$
is
![]() $(\mathfrak {a}\mathcal {D}_{F})^{-1}\otimes \mathbb {G}_{\mathrm {m}}$
. For any
$(\mathfrak {a}\mathcal {D}_{F})^{-1}\otimes \mathbb {G}_{\mathrm {m}}$
. For any
![]() $\eta \in \mathfrak {a}$
, we denote by
$\eta \in \mathfrak {a}$
, we denote by
![]() $\mathfrak {X}^{\eta }$
the element of
$\mathfrak {X}^{\eta }$
the element of
 $\mathcal {O}\left ((\mathfrak {a}\mathcal {D}_{F})^{-1}\otimes \mathbb {G}_{\mathrm {m}}\right )$
which the character
$\mathcal {O}\left ((\mathfrak {a}\mathcal {D}_{F})^{-1}\otimes \mathbb {G}_{\mathrm {m}}\right )$
which the character
![]() $\eta $
defines. We have an
$\eta $
defines. We have an
![]() $\mathcal {O}_{F}$
-linear homomorphism
$\mathcal {O}_{F}$
-linear homomorphism
 $$ \begin{align*} q: \mathfrak{b} \to (\mathfrak{a}\mathcal{D}_{F})^{-1}\otimes \mathbb{G}_{\mathrm{m}}\left(\bar{S}_{\sigma}^{0}\right) \end{align*} $$
$$ \begin{align*} q: \mathfrak{b} \to (\mathfrak{a}\mathcal{D}_{F})^{-1}\otimes \mathbb{G}_{\mathrm{m}}\left(\bar{S}_{\sigma}^{0}\right) \end{align*} $$
defined by
 $\xi \mapsto \left (\mathfrak {X}^{\eta }\mapsto q^{\xi \eta }\right )$
with
$\xi \mapsto \left (\mathfrak {X}^{\eta }\mapsto q^{\xi \eta }\right )$
with
![]() $\xi \in \mathfrak {b}$
and
$\xi \in \mathfrak {b}$
and
![]() $\eta \in \mathfrak {a}$
. By Mumford’s construction, we obtain the semi-abelian scheme
$\eta \in \mathfrak {a}$
. By Mumford’s construction, we obtain the semi-abelian scheme
![]() $\mathrm {Tate}_{\mathfrak {a},\mathfrak {b}}(q)$
over
$\mathrm {Tate}_{\mathfrak {a},\mathfrak {b}}(q)$
over
![]() $\bar {S}_{\sigma }$
such that its restriction to
$\bar {S}_{\sigma }$
such that its restriction to
![]() $\bar {S}_{\sigma }^{0}$
is an abelian scheme [Reference Rapoport36, §4]. It admits a natural
$\bar {S}_{\sigma }^{0}$
is an abelian scheme [Reference Rapoport36, §4]. It admits a natural
![]() $\mathcal {O}_{F}$
-action. Over
$\mathcal {O}_{F}$
-action. Over
![]() $\bar {S}_{\sigma }^{0}$
, we have a natural exact sequence
$\bar {S}_{\sigma }^{0}$
, we have a natural exact sequence

which defines, for any unramified cusp
![]() $(\mathfrak {a},\mathfrak {b},\phi _{N})$
, a
$(\mathfrak {a},\mathfrak {b},\phi _{N})$
, a
![]() $\Gamma _{00}(N)$
-structure on
$\Gamma _{00}(N)$
-structure on
 $\mathrm {Tate}_{\mathfrak {a},\mathfrak {b}}(q)\rvert _{\bar {S}_{\sigma }^{0}}$
using
$\mathrm {Tate}_{\mathfrak {a},\mathfrak {b}}(q)\rvert _{\bar {S}_{\sigma }^{0}}$
using
![]() $\phi _{N}$
. Moreover, the natural isomorphism
$\phi _{N}$
. Moreover, the natural isomorphism
 $$ \begin{align*} \left((\mathfrak{a}\mathcal{D}_{F})^{-1}\otimes \mathbb{G}_{\mathrm{m}}\right)\otimes_{\mathcal{O}_{F}}\mathfrak{c} \to (\mathfrak{b}\mathcal{D}_{F})^{-1}\otimes \mathbb{G}_{\mathrm{m}} \end{align*} $$
$$ \begin{align*} \left((\mathfrak{a}\mathcal{D}_{F})^{-1}\otimes \mathbb{G}_{\mathrm{m}}\right)\otimes_{\mathcal{O}_{F}}\mathfrak{c} \to (\mathfrak{b}\mathcal{D}_{F})^{-1}\otimes \mathbb{G}_{\mathrm{m}} \end{align*} $$
induces a
![]() $\mathfrak {c}$
-polarization
$\mathfrak {c}$
-polarization
 $$ \begin{align*} \lambda_{\mathfrak{a},\mathfrak{b}}: \mathrm{Tate}_{\mathfrak{a},\mathfrak{b}}(q)\rvert_{\bar{S}_{\sigma}^{0}} \otimes_{\mathcal{O}_{F}} \mathfrak{c}\to \mathrm{Tate}_{\mathfrak{b},\mathfrak{a}}(q)\rvert_{\bar{S}_{\sigma}^{0}} \simeq \left(\mathrm{Tate}_{\mathfrak{a},\mathfrak{b}}(q)\rvert_{\bar{S}_{\sigma}^{0}}\right)^{\vee}. \end{align*} $$
$$ \begin{align*} \lambda_{\mathfrak{a},\mathfrak{b}}: \mathrm{Tate}_{\mathfrak{a},\mathfrak{b}}(q)\rvert_{\bar{S}_{\sigma}^{0}} \otimes_{\mathcal{O}_{F}} \mathfrak{c}\to \mathrm{Tate}_{\mathfrak{b},\mathfrak{a}}(q)\rvert_{\bar{S}_{\sigma}^{0}} \simeq \left(\mathrm{Tate}_{\mathfrak{a},\mathfrak{b}}(q)\rvert_{\bar{S}_{\sigma}^{0}}\right)^{\vee}. \end{align*} $$
By these data we consider the Tate object
 $\mathrm {Tate}_{\mathfrak {a},\mathfrak {b}}(q)\rvert _{\bar {S}_{\sigma }^{0}}$
as an HBAV over
$\mathrm {Tate}_{\mathfrak {a},\mathfrak {b}}(q)\rvert _{\bar {S}_{\sigma }^{0}}$
as an HBAV over
![]() $\bar {S}_{\sigma }^{0}$
, which yields a morphism
$\bar {S}_{\sigma }^{0}$
, which yields a morphism
![]() $\bar {S} {}_{\sigma }^{0}\to M(\mu _{N},\mathfrak {c})$
. Then the toroidal compactification
$\bar {S} {}_{\sigma }^{0}\to M(\mu _{N},\mathfrak {c})$
. Then the toroidal compactification
![]() $\bar {M}^{\mathscr {D}(\mathfrak {c})}(\mu _{N},\mathfrak {c})$
of
$\bar {M}^{\mathscr {D}(\mathfrak {c})}(\mu _{N},\mathfrak {c})$
of
![]() $M(\mu _{N},\mathfrak {c})$
over
$M(\mu _{N},\mathfrak {c})$
over
![]() $\mathcal {O}_{K}$
with respect to
$\mathcal {O}_{K}$
with respect to
![]() $\mathscr {D}(\mathfrak {c})$
– which we also denote by
$\mathscr {D}(\mathfrak {c})$
– which we also denote by
![]() $\bar {M}(\mu _{N},\mathfrak {c})$
if no confusion will occur – is constructed in such a way as to satisfy the following (see [Reference Rapoport36, Théorème 6.18] and [Reference Dimitrov23, Théorème 7.2 (i)]):
$\bar {M}(\mu _{N},\mathfrak {c})$
if no confusion will occur – is constructed in such a way as to satisfy the following (see [Reference Rapoport36, Théorème 6.18] and [Reference Dimitrov23, Théorème 7.2 (i)]):
-
•
 $\bar {M}(\mu _{N},\mathfrak {c})$
is projective and smooth over
$\bar {M}(\mu _{N},\mathfrak {c})$
is projective and smooth over
 $\mathcal {O}_{K}$
.
$\mathcal {O}_{K}$
. -
•
 $M(\mu _{N},\mathfrak {c})$
is an open subscheme of
$M(\mu _{N},\mathfrak {c})$
is an open subscheme of
 $\bar {M}(\mu _{N},\mathfrak {c})$
which is fiberwise dense and the complement D of
$\bar {M}(\mu _{N},\mathfrak {c})$
which is fiberwise dense and the complement D of
 $M(\mu _{N},\mathfrak {c})$
is a normal crossing divisor. In particular,
$M(\mu _{N},\mathfrak {c})$
is a normal crossing divisor. In particular,
 $M(\mu _{N},\mathfrak {c})$
is quasi-compact.
$M(\mu _{N},\mathfrak {c})$
is quasi-compact. -
• The formal completion
 $\bar {M}(\mu _{N},\mathfrak {c})\rvert ^{\wedge }_{D}$
of
$\bar {M}(\mu _{N},\mathfrak {c})\rvert ^{\wedge }_{D}$
of
 $\bar {M}(\mu _{N},\mathfrak {c})$
along the boundary divisor D contains as a formal open subscheme, where the disjoint union runs over the set of isomorphism classes of unramified cusps.
$\bar {M}(\mu _{N},\mathfrak {c})$
along the boundary divisor D contains as a formal open subscheme, where the disjoint union runs over the set of isomorphism classes of unramified cusps. $$ \begin{align*} \coprod \hat{S}_{\mathscr{C}(\mathfrak{a},\mathfrak{b})}/U_{N} \end{align*} $$
$$ \begin{align*} \coprod \hat{S}_{\mathscr{C}(\mathfrak{a},\mathfrak{b})}/U_{N} \end{align*} $$
-
• The universal HBAV
 $A^{\mathrm {un}}$
over
$A^{\mathrm {un}}$
over
 $M(\mu _{N},\mathfrak {c})$
extends to a semi-abelian scheme
$M(\mu _{N},\mathfrak {c})$
extends to a semi-abelian scheme
 $\bar {A}^{\mathrm {un}}$
with
$\bar {A}^{\mathrm {un}}$
with
 $\mathcal {O}_{F}$
-action over
$\mathcal {O}_{F}$
-action over
 $\bar {M}(\mu _{N},\mathfrak {c})$
such that for any
$\bar {M}(\mu _{N},\mathfrak {c})$
such that for any
 $\sigma \in \mathscr {C}(\mathfrak {a},\mathfrak {b})$
, the pullback of
$\sigma \in \mathscr {C}(\mathfrak {a},\mathfrak {b})$
, the pullback of
 $\bar {A}^{\mathrm {un}}$
by the restriction to
$\bar {A}^{\mathrm {un}}$
by the restriction to
 $\bar {S}_{\sigma }^{0}$
of the unique algebraization
$\bar {S}_{\sigma }^{0}$
of the unique algebraization
 $\bar {S} {}_{\sigma }\to \bar {M}(\mu _{N},\mathfrak {c})$
of the map
$\bar {S} {}_{\sigma }\to \bar {M}(\mu _{N},\mathfrak {c})$
of the map
 $\hat {S}_{\sigma }\to \bar {M}(\mu _{N},\mathfrak {c})\rvert _{D}^{\wedge }$
for any unramified cusp
$\hat {S}_{\sigma }\to \bar {M}(\mu _{N},\mathfrak {c})\rvert _{D}^{\wedge }$
for any unramified cusp
 $(\mathfrak {a},\mathfrak {b},\phi _{N})$
is isomorphic to
$(\mathfrak {a},\mathfrak {b},\phi _{N})$
is isomorphic to
 $ \mathrm {Tate}_{\mathfrak {a},\mathfrak {b}}(q)\rvert _{\bar {S}_{\sigma }^{0}}$
.
$ \mathrm {Tate}_{\mathfrak {a},\mathfrak {b}}(q)\rvert _{\bar {S}_{\sigma }^{0}}$
.
3.1.3 Strict neighborhoods of the ordinary locus and their integral models
Let
![]() $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})$
be the p-adic formal completion of
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})$
be the p-adic formal completion of
![]() $\bar {M}(\mu _{N},\mathfrak {c})$
. Let
$\bar {M}(\mu _{N},\mathfrak {c})$
. Let
![]() $\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})$
be its Raynaud generic fiber. Let
$\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})$
be its Raynaud generic fiber. Let
![]() $ \mathcal {M}(\mu _{N},\mathfrak {c})$
be the analytification of the scheme
$ \mathcal {M}(\mu _{N},\mathfrak {c})$
be the analytification of the scheme
![]() $M(\mu _{N},\mathfrak {c})\otimes _{\mathcal {O}_{K}}K$
, which is a Zariski open subvariety of
$M(\mu _{N},\mathfrak {c})\otimes _{\mathcal {O}_{K}}K$
, which is a Zariski open subvariety of
![]() $\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})$
. The semi-abelian scheme
$\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})$
. The semi-abelian scheme
![]() $\bar {A}^{\mathrm {un}}$
defines semi-abelian objects
$\bar {A}^{\mathrm {un}}$
defines semi-abelian objects
![]() $\bar {\mathfrak {A}}^{\mathrm {un}}$
over
$\bar {\mathfrak {A}}^{\mathrm {un}}$
over
![]() $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})$
and
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})$
and
![]() $\bar {\mathcal {A}}^{\mathrm {un}}$
over
$\bar {\mathcal {A}}^{\mathrm {un}}$
over
![]() $\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})$
by taking the p-adic completion and the Raynaud generic fiber. For the zero section e of
$\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})$
by taking the p-adic completion and the Raynaud generic fiber. For the zero section e of
![]() $\bar {A}^{\mathrm {un}}$
, put
$\bar {A}^{\mathrm {un}}$
, put
 $\omega _{\bar {A}^{\mathrm {un}}}=e^{*}\Omega ^{1}_{\bar {A}^{\mathrm {un}}/\bar {M}\left (\mu _{N},\mathfrak {c}\right )}$
. For any g-tuple
$\omega _{\bar {A}^{\mathrm {un}}}=e^{*}\Omega ^{1}_{\bar {A}^{\mathrm {un}}/\bar {M}\left (\mu _{N},\mathfrak {c}\right )}$
. For any g-tuple
 $\kappa =\left (k_{\beta }\right )_{\beta \in \mathbb {B}_{F}}$
in
$\kappa =\left (k_{\beta }\right )_{\beta \in \mathbb {B}_{F}}$
in
![]() $\mathbb {Z}$
, we define
$\mathbb {Z}$
, we define
 $$ \begin{align*} \omega_{\bar{A}^{\mathrm{un}},\beta}=\omega_{\bar{A}^{\mathrm{un}}}\otimes_{\mathcal{O}_{F}, \beta}\mathcal{O}_{K},\qquad \omega^{\kappa}_{\bar{A}^{\mathrm{un}}}=\bigotimes_{\beta\in \mathbb{B}_{F}} \omega_{\bar{A} {}^{\mathrm{un}},\beta}^{\otimes k_{\beta}}. \end{align*} $$
$$ \begin{align*} \omega_{\bar{A}^{\mathrm{un}},\beta}=\omega_{\bar{A}^{\mathrm{un}}}\otimes_{\mathcal{O}_{F}, \beta}\mathcal{O}_{K},\qquad \omega^{\kappa}_{\bar{A}^{\mathrm{un}}}=\bigotimes_{\beta\in \mathbb{B}_{F}} \omega_{\bar{A} {}^{\mathrm{un}},\beta}^{\otimes k_{\beta}}. \end{align*} $$
We also define
![]() $\omega _{\bar {\mathcal {A}}^{\mathrm {un}},\beta }$
and
$\omega _{\bar {\mathcal {A}}^{\mathrm {un}},\beta }$
and
![]() $\omega ^{\kappa }_{\bar {\mathcal {A}}^{\mathrm {un}}}$
similarly. For any
$\omega ^{\kappa }_{\bar {\mathcal {A}}^{\mathrm {un}}}$
similarly. For any
![]() $\beta \in \mathbb {B}_{F}$
, let
$\beta \in \mathbb {B}_{F}$
, let
![]() $h_{\beta }$
be the
$h_{\beta }$
be the
![]() $\beta $
-partial Hasse invariant, which is a section of the invertible sheaf
$\beta $
-partial Hasse invariant, which is a section of the invertible sheaf
 $\omega _{\bar {A}^{\mathrm {un}},\sigma ^{-1} \circ \beta }^{p}\otimes \omega _{\bar {A}^{\mathrm {un}},\beta }^{-1}$
on
$\omega _{\bar {A}^{\mathrm {un}},\sigma ^{-1} \circ \beta }^{p}\otimes \omega _{\bar {A}^{\mathrm {un}},\beta }^{-1}$
on
![]() $\bar {M}(\mu _{N},\mathfrak {c})\times \mathscr {S}_{1}$
[Reference Goren and Kassaei27, §2.5] (see also [Reference Andreatta and Goren2, §7] and [Reference Emerton, Reduzzi and Xiao24, §3.1]). For any extension
$\bar {M}(\mu _{N},\mathfrak {c})\times \mathscr {S}_{1}$
[Reference Goren and Kassaei27, §2.5] (see also [Reference Andreatta and Goren2, §7] and [Reference Emerton, Reduzzi and Xiao24, §3.1]). For any extension
![]() $L/K$
of complete valuation fields, any HBAV A over
$L/K$
of complete valuation fields, any HBAV A over
![]() $\mathcal {O}_{L}$
, and any
$\mathcal {O}_{L}$
, and any
![]() $\beta \in \mathbb {B}_{F}$
, consider the element P of
$\beta \in \mathbb {B}_{F}$
, consider the element P of
![]() $\bar {\mathcal {M}} (\mu _{N},\mathfrak {c})(L)$
induced by A and a lift
$\bar {\mathcal {M}} (\mu _{N},\mathfrak {c})(L)$
induced by A and a lift
![]() $\tilde {h}_{\beta }$
of
$\tilde {h}_{\beta }$
of
![]() $h_{\beta }$
as a section of
$h_{\beta }$
as a section of
 $\omega _{\bar {A}^{\mathrm {un}},\sigma ^{-1}\circ \beta }^{p}\otimes \omega _{\bar {A}^{\mathrm {un}},\beta }^{-1}$
over an open neighborhood of P. Then we have the equality of truncated valuations
$\omega _{\bar {A}^{\mathrm {un}},\sigma ^{-1}\circ \beta }^{p}\otimes \omega _{\bar {A}^{\mathrm {un}},\beta }^{-1}$
over an open neighborhood of P. Then we have the equality of truncated valuations
 $$ \begin{align*} \mathrm{Hdg}_{\beta}(A)=v_{p}\left(\tilde{h}_{\beta}(P)\right). \end{align*} $$
$$ \begin{align*} \mathrm{Hdg}_{\beta}(A)=v_{p}\left(\tilde{h}_{\beta}(P)\right). \end{align*} $$
If
![]() $P\in \bar {\mathcal {M}}(\mu _{N},\mathfrak {c})(L)$
corresponds to a semi-abelian scheme A over
$P\in \bar {\mathcal {M}}(\mu _{N},\mathfrak {c})(L)$
corresponds to a semi-abelian scheme A over
![]() $\mathcal {O}_{L}$
which is not an abelian scheme, then we put
$\mathcal {O}_{L}$
which is not an abelian scheme, then we put
 $\mathrm {Hdg}_{\beta }(A)=v_{p}\left (\tilde {h}_{\beta }(P)\right )=0$
.
$\mathrm {Hdg}_{\beta }(A)=v_{p}\left (\tilde {h}_{\beta }(P)\right )=0$
.
Let
 $\underline {v}=\left (v_{\beta }\right )_{\beta \in \mathbb {B}_{F}}$
be a g-tuple in
$\underline {v}=\left (v_{\beta }\right )_{\beta \in \mathbb {B}_{F}}$
be a g-tuple in
![]() $[0,1]\cap \mathbb {Q}$
. We denote by
$[0,1]\cap \mathbb {Q}$
. We denote by
![]() $\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
and
$\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
and
![]() $\mathcal {M}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
the admissible open subsets of
$\mathcal {M}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
the admissible open subsets of
![]() $\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})$
and
$\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})$
and
![]() $\mathcal {M}(\mu _{N},\mathfrak {c})$
defined by
$\mathcal {M}(\mu _{N},\mathfrak {c})$
defined by
 $v_{p}\left (\tilde {h}_{\beta }(P)\right )\leq v_{\beta }$
for any
$v_{p}\left (\tilde {h}_{\beta }(P)\right )\leq v_{\beta }$
for any
![]() $\beta \in \mathbb {B}_{F}$
, respectively. Note that
$\beta \in \mathbb {B}_{F}$
, respectively. Note that
![]() $\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
is quasi-compact. We define its integral model
$\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
is quasi-compact. We define its integral model
![]() $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
as follows: Write
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
as follows: Write
![]() $v_{\beta }=a_{\beta }/b_{\beta }$
with nonnegative integers
$v_{\beta }=a_{\beta }/b_{\beta }$
with nonnegative integers
![]() $a_{\beta }$
and
$a_{\beta }$
and
![]() $b_{\beta }\neq 0$
. Take a formal open covering
$b_{\beta }\neq 0$
. Take a formal open covering
![]() $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})=\bigcup \mathfrak {U}_{i}$
such that every
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})=\bigcup \mathfrak {U}_{i}$
such that every
![]() $h_{\beta }$
lifts to a section
$h_{\beta }$
lifts to a section
![]() $\tilde {h}_{\beta }$
on each
$\tilde {h}_{\beta }$
on each
![]() $\mathfrak {U}_{i}$
. Consider the formal scheme whose restriction to each
$\mathfrak {U}_{i}$
. Consider the formal scheme whose restriction to each
![]() $\mathfrak {U}_{i}$
is the admissible blowup of
$\mathfrak {U}_{i}$
is the admissible blowup of
![]() $\mathfrak {U}_{i}$
along the ideal
$\mathfrak {U}_{i}$
along the ideal
 $\left (p^{a_{\beta }},\tilde {h}_{\beta }^{b_{\beta }}\right )$
, and its locus where this ideal is generated by
$\left (p^{a_{\beta }},\tilde {h}_{\beta }^{b_{\beta }}\right )$
, and its locus where this ideal is generated by
 $\tilde {h}_{\beta }^{b_{\beta }}$
. Repeat this for any
$\tilde {h}_{\beta }^{b_{\beta }}$
. Repeat this for any
![]() $\beta \in \mathbb {B}_{F}$
and define
$\beta \in \mathbb {B}_{F}$
and define
![]() $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
as the normalization in
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
as the normalization in
![]() $\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
of the resulting formal scheme. We denote the special fibers of
$\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
of the resulting formal scheme. We denote the special fibers of
![]() $\bar {M}(\mu _{N},\mathfrak {c})$
and
$\bar {M}(\mu _{N},\mathfrak {c})$
and
![]() $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c}) \left (\underline {v}\right )$
by
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c}) \left (\underline {v}\right )$
by
![]() $\bar {M}(\mu _{N},\mathfrak {c})_{k}$
and
$\bar {M}(\mu _{N},\mathfrak {c})_{k}$
and
![]() $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )_{k}$
, respectively. We also denote by
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )_{k}$
, respectively. We also denote by
![]() $\mathfrak {M}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
the complement in
$\mathfrak {M}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
the complement in
![]() $\bar {\mathfrak {M}} (\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
of the boundary divisor
$\bar {\mathfrak {M}} (\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
of the boundary divisor
![]() $D_{k}$
of the special fiber. Then the open immersion
$D_{k}$
of the special fiber. Then the open immersion
![]() $\mathfrak {M}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )\to \bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
is of finite type and [Reference de Jong19, Proposition 7.2.4] implies that
$\mathfrak {M}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )\to \bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
is of finite type and [Reference de Jong19, Proposition 7.2.4] implies that
 $\mathfrak {M}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )^{\mathrm {rig}}$
is quasi-compact.
$\mathfrak {M}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )^{\mathrm {rig}}$
is quasi-compact.
Let v be an element of
![]() $[0,1]\cap \mathbb {Q}$
. When
$[0,1]\cap \mathbb {Q}$
. When
![]() $v_{\beta }=v$
for any
$v_{\beta }=v$
for any
![]() $\beta \in \mathbb {B}_{F}$
, we write
$\beta \in \mathbb {B}_{F}$
, we write
![]() $\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
as
$\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
as
![]() $\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})(v)$
. Moreover, we denote by
$\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})(v)$
. Moreover, we denote by
![]() $\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})(v_{\mathrm {tot}})$
the quasi-compact admissible open subset defined similarly to
$\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})(v_{\mathrm {tot}})$
the quasi-compact admissible open subset defined similarly to
![]() $\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})(v)$
with the usual Hasse invariant
$\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})(v)$
with the usual Hasse invariant
 $$ \begin{align*} h_{\mathrm{tot}}=\prod_{\beta\in \mathbb{B}_{F}}h_{\beta} \end{align*} $$
$$ \begin{align*} h_{\mathrm{tot}}=\prod_{\beta\in \mathbb{B}_{F}}h_{\beta} \end{align*} $$
instead of
![]() $h_{\beta }$
s. We also define similar spaces for these two variants, such as
$h_{\beta }$
s. We also define similar spaces for these two variants, such as
![]() $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(v)$
and
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(v)$
and
![]() $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(v_{\mathrm {tot}})$
. Note that
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(v_{\mathrm {tot}})$
. Note that
![]() $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)$
is just the formal open subscheme of
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)$
is just the formal open subscheme of
![]() $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})$
over which all the
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})$
over which all the
![]() $\beta $
-partial Hasse invariants are invertible.
$\beta $
-partial Hasse invariants are invertible.
The formal scheme
![]() $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)$
is also a formal open subscheme of
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)$
is also a formal open subscheme of
![]() $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
containing
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
containing
![]() $D_{k}$
. Let
$D_{k}$
. Let
![]() $\mathrm {sp}:\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})\to \bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})_{k}$
be the specialization map with respect to
$\mathrm {sp}:\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})\to \bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})_{k}$
be the specialization map with respect to
![]() $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})$
. Then [Reference de Jong19, Propositions 7.2.1 and 7.2.4] yields
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})$
. Then [Reference de Jong19, Propositions 7.2.1 and 7.2.4] yields
 $$ \begin{align} \mathfrak{M}(\mu_{N},\mathfrak{c})\left(\underline{v}\right)^{\mathrm{rig}}=\bar{\mathcal{M}}(\mu_{N},\mathfrak{c})\left(\underline{v}\right)\setminus \mathrm{sp}^{-1}(D_{k}). \end{align} $$
$$ \begin{align} \mathfrak{M}(\mu_{N},\mathfrak{c})\left(\underline{v}\right)^{\mathrm{rig}}=\bar{\mathcal{M}}(\mu_{N},\mathfrak{c})\left(\underline{v}\right)\setminus \mathrm{sp}^{-1}(D_{k}). \end{align} $$
Let R be a topological
![]() $\mathcal {O}_{K}$
-algebra which is idyllic with respect to the p-adic topology [Reference Abbes1, Définition 1.10.1]. By [Reference Abbes1, Corollaire 2.13.9], any morphism
$\mathcal {O}_{K}$
-algebra which is idyllic with respect to the p-adic topology [Reference Abbes1, Définition 1.10.1]. By [Reference Abbes1, Corollaire 2.13.9], any morphism
 $\hat {f}:\mathrm {Spf}(R)\to \bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})$
has a unique algebraization
$\hat {f}:\mathrm {Spf}(R)\to \bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})$
has a unique algebraization
![]() $f:\mathrm {Spec}(R)\to \bar {M}(\mu _{N},\mathfrak {c})$
, and we have a semi-abelian scheme
$f:\mathrm {Spec}(R)\to \bar {M}(\mu _{N},\mathfrak {c})$
, and we have a semi-abelian scheme
![]() $G_{R}=f^{*}\bar {A}^{\mathrm {un}}$
over
$G_{R}=f^{*}\bar {A}^{\mathrm {un}}$
over
![]() $\mathrm {Spec}(R)$
. Taking the reduction modulo p, we see that
$\mathrm {Spec}(R)$
. Taking the reduction modulo p, we see that
![]() $\hat {f}$
factors through
$\hat {f}$
factors through
![]() $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)$
if and only if
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)$
if and only if
![]() $G_{R}$
is ordinary.
$G_{R}$
is ordinary.
Let
![]() $\mathbf {NAdm}$
be the category of admissible p-adic formal
$\mathbf {NAdm}$
be the category of admissible p-adic formal
![]() $\mathcal {O}_{K}$
-algebras R such that R is normal. Note that we have
$\mathcal {O}_{K}$
-algebras R such that R is normal. Note that we have
![]() $R[1/p]^{\circ }=R$
by [Reference Bosch, Güntzer and Remmert10, remark after Proposition 6.3.4/1]. By [Reference Rapoport36, Lemme 3.1], we can see as in [Reference Andreatta, Iovita and Pilloni3, Proposition 5.2.1.1] that any morphism
$R[1/p]^{\circ }=R$
by [Reference Bosch, Güntzer and Remmert10, remark after Proposition 6.3.4/1]. By [Reference Rapoport36, Lemme 3.1], we can see as in [Reference Andreatta, Iovita and Pilloni3, Proposition 5.2.1.1] that any morphism
 $\mathrm {Sp}(R[1/p])\to \mathfrak {M}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )^{\mathrm {rig}}$
corresponds uniquely to an isomorphism class of an HBAV A over
$\mathrm {Sp}(R[1/p])\to \mathfrak {M}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )^{\mathrm {rig}}$
corresponds uniquely to an isomorphism class of an HBAV A over
![]() $\mathrm {Spec}(R)$
such that
$\mathrm {Spec}(R)$
such that
![]() $\mathrm {Hdg}_{\beta }(A_{x})\leq v_{\beta }$
for
$\mathrm {Hdg}_{\beta }(A_{x})\leq v_{\beta }$
for
![]() $x\in \mathrm {Sp}(R[1/p])$
.
$x\in \mathrm {Sp}(R[1/p])$
.
We give a proof of the following lemma for lack of a reference:
Lemma 3.1. Let
![]() $L/K$
be an extension of complete valuation fields. Let
$L/K$
be an extension of complete valuation fields. Let
![]() $\mathcal {X}$
be a connected smooth rigid analytic variety over L and let
$\mathcal {X}$
be a connected smooth rigid analytic variety over L and let
![]() $\mathcal {F}$
be an invertible sheaf on
$\mathcal {F}$
be an invertible sheaf on
![]() $\mathcal {X}$
. Suppose that
$\mathcal {X}$
. Suppose that
![]() $f\in \mathcal {F}(\mathcal {X})$
vanishes on a nonempty admissible open subset
$f\in \mathcal {F}(\mathcal {X})$
vanishes on a nonempty admissible open subset
![]() $\mathcal {U}$
of
$\mathcal {U}$
of
![]() $\mathcal {X}$
. Then
$\mathcal {X}$
. Then
![]() $f=0$
.
$f=0$
.
Proof. Take an admissible affinoid covering
![]() $\mathcal {X}=\bigcup _{i\in I} \mathcal {X}_{i}$
such that
$\mathcal {X}=\bigcup _{i\in I} \mathcal {X}_{i}$
such that
![]() $\mathcal {X}_{i}$
is connected and
$\mathcal {X}_{i}$
is connected and
![]() $\mathcal {F}$
is trivial on
$\mathcal {F}$
is trivial on
![]() $\mathcal {X}_{i}$
for any
$\mathcal {X}_{i}$
for any
![]() $i\in I$
. We have
$i\in I$
. We have
![]() $\mathcal {X}_{i_{0}}\cap \mathcal {U}\neq \emptyset $
for some
$\mathcal {X}_{i_{0}}\cap \mathcal {U}\neq \emptyset $
for some
![]() $i_{0}$
. Then [Reference Fresnel and van der Put25, Exercise 4.6.3] implies
$i_{0}$
. Then [Reference Fresnel and van der Put25, Exercise 4.6.3] implies
![]() $f\rvert _{\mathcal {X}_{i_{0}}}=0$
.
$f\rvert _{\mathcal {X}_{i_{0}}}=0$
.
Put
![]() $I_{0}=\left \{i\in I\mid f\rvert _{\mathcal {X}_{i}}=0\right \}$
, which is nonempty. [Reference Fresnel and van der Put25, Exercise 4.6.3] also implies that
$I_{0}=\left \{i\in I\mid f\rvert _{\mathcal {X}_{i}}=0\right \}$
, which is nonempty. [Reference Fresnel and van der Put25, Exercise 4.6.3] also implies that
![]() $\mathcal {X}_{i}\cap \mathcal {X}_{j}=\emptyset $
for any
$\mathcal {X}_{i}\cap \mathcal {X}_{j}=\emptyset $
for any
![]() $i\in I_{0}$
and
$i\in I_{0}$
and
![]() $j\in I_{1}:=I\setminus I_{0}$
. Then for the subsets
$j\in I_{1}:=I\setminus I_{0}$
. Then for the subsets
 $$ \begin{align*} \mathcal{X}_{0}=\bigcup_{i\in I_{0}} \mathcal{X}_{i},\qquad \mathcal{X}_{1}=\bigcup_{i\in I_{1}} \mathcal{X}_{i} \end{align*} $$
$$ \begin{align*} \mathcal{X}_{0}=\bigcup_{i\in I_{0}} \mathcal{X}_{i},\qquad \mathcal{X}_{1}=\bigcup_{i\in I_{1}} \mathcal{X}_{i} \end{align*} $$
and
![]() $s\in \{0,1\}$
, the intersection
$s\in \{0,1\}$
, the intersection
![]() $\mathcal {X}_{s}\cap \mathcal {X}_{i}$
equals
$\mathcal {X}_{s}\cap \mathcal {X}_{i}$
equals
![]() $\mathcal {X}_{i}$
if
$\mathcal {X}_{i}$
if
![]() $i\in I_{s}$
and
$i\in I_{s}$
and
![]() $\emptyset $
if
$\emptyset $
if
![]() $i\notin I_{s}$
. Hence
$i\notin I_{s}$
. Hence
![]() $\mathcal {X}=\mathcal {X}_{0}\coprod \mathcal {X}_{1}$
is an admissible covering of
$\mathcal {X}=\mathcal {X}_{0}\coprod \mathcal {X}_{1}$
is an admissible covering of
![]() $\mathcal {X}$
. Since
$\mathcal {X}$
. Since
![]() $\mathcal {X}$
is connected, we obtain
$\mathcal {X}$
is connected, we obtain
![]() $\mathcal {X}=\mathcal {X}_{0}$
and
$\mathcal {X}=\mathcal {X}_{0}$
and
![]() $f=0$
.
$f=0$
.
Lemma 3.2. Let
![]() $L/K$
be an extension of complete valuation fields. Let
$L/K$
be an extension of complete valuation fields. Let
![]() $\mathfrak {R}$
be an admissible formal
$\mathfrak {R}$
be an admissible formal
![]() $\mathcal {O}_{L}$
-algebra such that
$\mathcal {O}_{L}$
-algebra such that
![]() $\mathfrak {R}[1/p]$
is reduced. Suppose that
$\mathfrak {R}[1/p]$
is reduced. Suppose that
![]() $\mathrm {Spec}(\mathfrak {R}/m_{L} \mathfrak {R})$
is reduced and connected. Then
$\mathrm {Spec}(\mathfrak {R}/m_{L} \mathfrak {R})$
is reduced and connected. Then
![]() $\mathrm {Sp}(\mathfrak {R}[1/p])$
is connected.
$\mathrm {Sp}(\mathfrak {R}[1/p])$
is connected.
Proof. Take a surjection
![]() $\mathcal {O}_{L}\langle T_{1},\dotsc ,T_{n}\rangle \to \mathfrak {R}$
. Then [Reference Bosch, Lütkebohmert and Raynaud11, Proposition 1.1] shows
$\mathcal {O}_{L}\langle T_{1},\dotsc ,T_{n}\rangle \to \mathfrak {R}$
. Then [Reference Bosch, Lütkebohmert and Raynaud11, Proposition 1.1] shows
![]() $(\mathfrak {R}[1/p])^{\circ }=\mathfrak {R}$
. Moreover, by [Reference Bosch, Güntzer and Remmert10, remark after Proposition 6.3.4/1]
$(\mathfrak {R}[1/p])^{\circ }=\mathfrak {R}$
. Moreover, by [Reference Bosch, Güntzer and Remmert10, remark after Proposition 6.3.4/1]
![]() $\mathfrak {R}$
is integrally closed in
$\mathfrak {R}$
is integrally closed in
![]() $\mathfrak {R}[1/p]$
. Thus we have bijections between the sets of connected components
$\mathfrak {R}[1/p]$
. Thus we have bijections between the sets of connected components
from which the lemma follows.
Lemma 3.3. Let
![]() $l/k$
be a finite extension and put
$l/k$
be a finite extension and put
![]() $W^{\prime }=W(l)$
. Let
$W^{\prime }=W(l)$
. Let
![]() $K^{\prime }$
be the composite field of K and
$K^{\prime }$
be the composite field of K and
![]() $\mathrm {Frac}(W^{\prime })$
in
$\mathrm {Frac}(W^{\prime })$
in
![]() $\bar {\mathbb {Q}}_{p}$
. Let R be a Noetherian W-algebra and let m be a maximal ideal of R with residue field l. Consider the natural maps
$\bar {\mathbb {Q}}_{p}$
. Let R be a Noetherian W-algebra and let m be a maximal ideal of R with residue field l. Consider the natural maps
induced by
![]() $R\to R/m=l$
. We denote the kernels of these maps by
$R\to R/m=l$
. We denote the kernels of these maps by
![]() $m^{\prime }$
, n, and
$m^{\prime }$
, n, and
![]() $n^{\prime }$
, respectively. Then the natural maps between complete local rings
$n^{\prime }$
, respectively. Then the natural maps between complete local rings
are bijective. In particular, we have isomorphisms
 $$ \begin{align*} (R\otimes_{W} \mathcal{O}_{K})^{\wedge}_{n}\to \left(R\otimes_{W}\mathcal{O}_{K^{\prime}}\right)_{n^{\prime}}^{\wedge}\gets(R\otimes_{W} W^{\prime})_{m^{\prime}}^{\wedge}\hat{\otimes}_{W^{\prime}}\mathcal{O}_{K^{\prime}}. \end{align*} $$
$$ \begin{align*} (R\otimes_{W} \mathcal{O}_{K})^{\wedge}_{n}\to \left(R\otimes_{W}\mathcal{O}_{K^{\prime}}\right)_{n^{\prime}}^{\wedge}\gets(R\otimes_{W} W^{\prime})_{m^{\prime}}^{\wedge}\hat{\otimes}_{W^{\prime}}\mathcal{O}_{K^{\prime}}. \end{align*} $$
Proof. For the first map, since R is Noetherian and
![]() $R/m=l$
is perfect, there exists a unique section
$R/m=l$
is perfect, there exists a unique section
![]() $W^{\prime }\to R^{\wedge }_{m}$
of the natural surjection
$W^{\prime }\to R^{\wedge }_{m}$
of the natural surjection
![]() $R^{\wedge }_{m}\to l$
. Thus we obtain a homomorphism of
$R^{\wedge }_{m}\to l$
. Thus we obtain a homomorphism of
![]() $W^{\prime }$
-algebras
$W^{\prime }$
-algebras
![]() $R\otimes _{W} W^{\prime }\to R^{\wedge }_{m}$
. This induces a map
$R\otimes _{W} W^{\prime }\to R^{\wedge }_{m}$
. This induces a map
![]() $(R\otimes _{W} W^{\prime })^{\wedge }_{m^{\prime }}\to R^{\wedge }_{m}$
, which gives the inverse of the first map.
$(R\otimes _{W} W^{\prime })^{\wedge }_{m^{\prime }}\to R^{\wedge }_{m}$
, which gives the inverse of the first map.
For the second map, since
![]() $p\in m$
and
$p\in m$
and
![]() $\mathcal {O}_{K}$
is totally ramified over W, we have
$\mathcal {O}_{K}$
is totally ramified over W, we have
![]() $n=(m,\pi _{K})$
. This yields
$n=(m,\pi _{K})$
. This yields
![]() $R^{\wedge }_{m}\hat {\otimes }_{W}\mathcal {O}_{K}\simeq (R\otimes _{W} \mathcal {O}_{K})^{\wedge }_{n}$
. The last assertion follows by applying them to
$R^{\wedge }_{m}\hat {\otimes }_{W}\mathcal {O}_{K}\simeq (R\otimes _{W} \mathcal {O}_{K})^{\wedge }_{n}$
. The last assertion follows by applying them to
![]() $R\otimes _{W} \mathcal {O}_{K}$
and
$R\otimes _{W} \mathcal {O}_{K}$
and
![]() $R\otimes _{W} W^{\prime }$
.
$R\otimes _{W} W^{\prime }$
.
Lemma 3.4. Let
![]() $\mathcal {X}_{v}$
be either of the rigid analytic varieties
$\mathcal {X}_{v}$
be either of the rigid analytic varieties
Then
![]() $\mathcal {X}_{v}\hat {\otimes }_{K}{\mathbb {C}_{p}}$
is connected for any
$\mathcal {X}_{v}\hat {\otimes }_{K}{\mathbb {C}_{p}}$
is connected for any
![]() $v\in [0,1)\cap \mathbb {Q}$
.
$v\in [0,1)\cap \mathbb {Q}$
.
Proof. Since
![]() $\mathcal {X}_{v}$
is separated, it is enough to show that for any sufficiently large finite extension
$\mathcal {X}_{v}$
is separated, it is enough to show that for any sufficiently large finite extension
![]() $K^{\prime }/K$
, the base extension
$K^{\prime }/K$
, the base extension
![]() $\mathcal {X}_{v}\hat {\otimes }_{K}{K^{\prime }}$
is connected [Reference Conrad17, Theorem 3.2.1]. Replacing K by
$\mathcal {X}_{v}\hat {\otimes }_{K}{K^{\prime }}$
is connected [Reference Conrad17, Theorem 3.2.1]. Replacing K by
![]() $K^{\prime }$
, we may assume that
$K^{\prime }$
, we may assume that
![]() $K^{\prime }=K$
and every connected component of
$K^{\prime }=K$
and every connected component of
![]() $\mathcal {X}_{v}$
has a K-rational point.
$\mathcal {X}_{v}$
has a K-rational point.
By Ribet’s theorem (see [Reference Goren26, Chapter 3, Theorem 6.19]), the ordinary locus
![]() ${\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)_{k}$
is geometrically connected. Then
${\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)_{k}$
is geometrically connected. Then
![]() $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)_{k}$
is also geometrically connected, since it is smooth over k and contains
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)_{k}$
is also geometrically connected, since it is smooth over k and contains
![]() ${\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)_{k}$
as a dense open subset. Since
${\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)_{k}$
as a dense open subset. Since
![]() $\mathcal {X}_{0}$
is the tube for the immersion
$\mathcal {X}_{0}$
is the tube for the immersion
![]() $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)_{k}\to \bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})$
, [Reference Berthelot9, Proposition 1.3.3] yields the lemma for
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)_{k}\to \bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})$
, [Reference Berthelot9, Proposition 1.3.3] yields the lemma for
![]() $v=0$
.
$v=0$
.
Consider the case of
![]() $v>0$
. Suppose that
$v>0$
. Suppose that
![]() $\mathcal {X}_{v}$
is not connected. Then we can take its connected component
$\mathcal {X}_{v}$
is not connected. Then we can take its connected component
![]() $\mathcal {U}$
which does not intersect
$\mathcal {U}$
which does not intersect
![]() $\mathcal {X}_{0}$
. Since
$\mathcal {X}_{0}$
. Since
![]() $\mathcal {U}$
is quasi-compact, there exists a finite admissible affinoid covering
$\mathcal {U}$
is quasi-compact, there exists a finite admissible affinoid covering
![]() $\mathcal {U}=\bigcup _{i=1}^{m} \mathcal {U}_{i}$
of
$\mathcal {U}=\bigcup _{i=1}^{m} \mathcal {U}_{i}$
of
![]() $\mathcal {U}$
such that any
$\mathcal {U}$
such that any
![]() $\beta $
-partial Hasse invariant can be lifted to a section over
$\beta $
-partial Hasse invariant can be lifted to a section over
![]() $\mathcal {U}_{i}$
. Using the maximal modulus principle on each
$\mathcal {U}_{i}$
. Using the maximal modulus principle on each
![]() $\mathcal {U}_{i}$
, we see that there exists a positive rational number
$\mathcal {U}_{i}$
, we see that there exists a positive rational number
![]() $\delta $
satisfying
$\delta $
satisfying
 $$ \begin{align*} \max\left\{\mathrm{Hdg}_{\beta}(x)\mid \beta\in \mathbb{B}_{F}\right\}\geq \delta \end{align*} $$
$$ \begin{align*} \max\left\{\mathrm{Hdg}_{\beta}(x)\mid \beta\in \mathbb{B}_{F}\right\}\geq \delta \end{align*} $$
for any
![]() $x\in \mathcal {U}$
. Then for any rational number
$x\in \mathcal {U}$
. Then for any rational number
![]() $\varepsilon $
satisfying
$\varepsilon $
satisfying
![]() $0<\varepsilon <\delta $
, we have
$0<\varepsilon <\delta $
, we have
![]() $\mathcal {X}_{\varepsilon }\cap \mathcal {U}=\emptyset $
.
$\mathcal {X}_{\varepsilon }\cap \mathcal {U}=\emptyset $
.
On the other hand, let us consider the specialization map
with respect to
![]() $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})$
. Take any
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})$
. Take any
![]() $P\in \mathcal {U}(K)$
and consider its specialization
$P\in \mathcal {U}(K)$
and consider its specialization
![]() $\bar {P}=\mathrm {sp}(P)$
. Since
$\bar {P}=\mathrm {sp}(P)$
. Since
![]() $P\notin \bar {\mathcal {M}}(\mu _{N},\mathfrak {c})(0)$
, the point
$P\notin \bar {\mathcal {M}}(\mu _{N},\mathfrak {c})(0)$
, the point
![]() $\bar {P}$
corresponds to an HBAV. By [Reference Goren and Kassaei27, (2.5.1)] and Lemma 3.3, the complete local ring of
$\bar {P}$
corresponds to an HBAV. By [Reference Goren and Kassaei27, (2.5.1)] and Lemma 3.3, the complete local ring of
![]() $M(\mu _{N},\mathfrak {c})$
at
$M(\mu _{N},\mathfrak {c})$
at
![]() $\bar {P}$
is isomorphic to the ring
$\bar {P}$
is isomorphic to the ring
![]() $\mathcal {O}_{K}\left [\left [t_{\beta }\mid \beta \in \mathbb {B}_{F}\right ]\right ]$
. Then [Reference de Jong19, Lemma 7.2.5] gives an identification
$\mathcal {O}_{K}\left [\left [t_{\beta }\mid \beta \in \mathbb {B}_{F}\right ]\right ]$
. Then [Reference de Jong19, Lemma 7.2.5] gives an identification
 $$ \begin{align} \mathrm{sp}^{-1}\left(\bar{P}\right)=\prod_{\beta\in\mathbb{B}_{F}} \mathcal{A}_{\beta}[0,1), \end{align} $$
$$ \begin{align} \mathrm{sp}^{-1}\left(\bar{P}\right)=\prod_{\beta\in\mathbb{B}_{F}} \mathcal{A}_{\beta}[0,1), \end{align} $$
where for any interval I we denote by
![]() $\mathcal {A}_{\beta } I$
the annulus over K with parameter
$\mathcal {A}_{\beta } I$
the annulus over K with parameter
![]() $t_{\beta }$
defined by the condition
$t_{\beta }$
defined by the condition
![]() $\left \lvert t_{\beta }\right \rvert \in I$
. By [Reference Goren and Kassaei27, §4.2], we may assume that the parameter
$\left \lvert t_{\beta }\right \rvert \in I$
. By [Reference Goren and Kassaei27, §4.2], we may assume that the parameter
![]() $t_{\beta }$
satisfies
$t_{\beta }$
satisfies
 $$ \begin{align} \mathrm{Hdg}_{\beta}(A)= \begin{cases} \min\{v_p(t_\beta(Q)),1\} & \left(\beta\in \tau\left(\bar{P}\right)\right) \\ 0 & \left(\beta\notin \tau\left(\bar{P}\right)\right) \end{cases} \end{align} $$
$$ \begin{align} \mathrm{Hdg}_{\beta}(A)= \begin{cases} \min\{v_p(t_\beta(Q)),1\} & \left(\beta\in \tau\left(\bar{P}\right)\right) \\ 0 & \left(\beta\notin \tau\left(\bar{P}\right)\right) \end{cases} \end{align} $$
for any
 $Q\in \mathrm {sp}^{-1}\left (\bar {P}\right )$
and for any
$Q\in \mathrm {sp}^{-1}\left (\bar {P}\right )$
and for any
![]() $\beta \in \mathbb {B}_{F}$
, where A is the HBAV corresponding to Q and
$\beta \in \mathbb {B}_{F}$
, where A is the HBAV corresponding to Q and
 $\tau \left (\bar {P}\right )$
is defined by [Reference Goren and Kassaei27, (2.3.3)].
$\tau \left (\bar {P}\right )$
is defined by [Reference Goren and Kassaei27, (2.3.3)].
Suppose
![]() $\mathcal {X}_{v}=\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})(v)$
. For any positive rational number
$\mathcal {X}_{v}=\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})(v)$
. For any positive rational number
![]() $\varepsilon $
, put
$\varepsilon $
, put
 $$ \begin{align*} \mathrm{sp}^{-1}\left(\bar{P}\right)(\varepsilon)^{\prime}=\prod_{\beta\in\tau\left(\bar{P}\right)} \mathcal{A}_{\beta}\left[p^{-\varepsilon},1\right)\times \prod_{\beta\notin\tau\left(\bar{P}\right)} \mathcal{A}_{\beta}[0,1). \end{align*} $$
$$ \begin{align*} \mathrm{sp}^{-1}\left(\bar{P}\right)(\varepsilon)^{\prime}=\prod_{\beta\in\tau\left(\bar{P}\right)} \mathcal{A}_{\beta}\left[p^{-\varepsilon},1\right)\times \prod_{\beta\notin\tau\left(\bar{P}\right)} \mathcal{A}_{\beta}[0,1). \end{align*} $$
Since
 $\mathrm {sp}^{-1}\left (\bar {P}\right )(v)^{\prime }$
is a connected admissible open subset of
$\mathrm {sp}^{-1}\left (\bar {P}\right )(v)^{\prime }$
is a connected admissible open subset of
![]() $\mathcal {X}_{v}$
containing P, it is contained in
$\mathcal {X}_{v}$
containing P, it is contained in
![]() $\mathcal {U}$
. However, for any
$\mathcal {U}$
. However, for any
![]() $\varepsilon $
satisfying
$\varepsilon $
satisfying
![]() $\varepsilon <\min \{\delta ,v\}$
, we have
$\varepsilon <\min \{\delta ,v\}$
, we have
 $$ \begin{align*} \emptyset \neq \mathrm{sp}^{-1}\left(\bar{P}\right)(\varepsilon)^{\prime}\subseteq \mathcal{X}_{\varepsilon}\cap \mathcal{U}, \end{align*} $$
$$ \begin{align*} \emptyset \neq \mathrm{sp}^{-1}\left(\bar{P}\right)(\varepsilon)^{\prime}\subseteq \mathcal{X}_{\varepsilon}\cap \mathcal{U}, \end{align*} $$
which is a contradiction.
When
![]() $\mathcal {X}_{v}=\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})(v_{\mathrm {tot}})$
, take any rational number
$\mathcal {X}_{v}=\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})(v_{\mathrm {tot}})$
, take any rational number
![]() $\varepsilon $
satisfying
$\varepsilon $
satisfying
![]() $0<\varepsilon <\min \{\delta ,v\}$
and
$0<\varepsilon <\min \{\delta ,v\}$
and
![]() $v_{p}\left (t_{\beta }(P)\right )\geq \varepsilon $
for any
$v_{p}\left (t_{\beta }(P)\right )\geq \varepsilon $
for any
![]() $\beta \in \mathbb {B}_{F}$
. Put
$\beta \in \mathbb {B}_{F}$
. Put
![]() $w=g^{-1}\varepsilon $
. Let
$w=g^{-1}\varepsilon $
. Let
![]() $\mathcal {V}$
be the admissible affinoid open subset of
$\mathcal {V}$
be the admissible affinoid open subset of
 $\mathrm {sp}^{-1}\left (\bar {P}\right )$
defined as
$\mathrm {sp}^{-1}\left (\bar {P}\right )$
defined as
 $$ \begin{align*} \mathcal{V}=\left\{\left(t_{\beta}\right)_{\beta\in \mathbb{B}_{F}}\in \prod_{\beta\in\mathbb{B}_{F}} \mathcal{A}_{\beta}\left[0,p^{-w}\right]\ \middle|\ \prod_{\beta\in\tau\left(\bar{P}\right)}\left\lvert t_{\beta}\right\rvert\geq p^{-v}\right\}. \end{align*} $$
$$ \begin{align*} \mathcal{V}=\left\{\left(t_{\beta}\right)_{\beta\in \mathbb{B}_{F}}\in \prod_{\beta\in\mathbb{B}_{F}} \mathcal{A}_{\beta}\left[0,p^{-w}\right]\ \middle|\ \prod_{\beta\in\tau\left(\bar{P}\right)}\left\lvert t_{\beta}\right\rvert\geq p^{-v}\right\}. \end{align*} $$
Since
![]() $P\in \mathcal {V}\subseteq \mathcal {X}_{v}$
and
$P\in \mathcal {V}\subseteq \mathcal {X}_{v}$
and
![]() $\mathcal {V}\cap \mathcal {X}_{\varepsilon }\neq \emptyset $
, by an argument as before we reduce ourselves to showing that
$\mathcal {V}\cap \mathcal {X}_{\varepsilon }\neq \emptyset $
, by an argument as before we reduce ourselves to showing that
![]() $\mathcal {V}$
is connected.
$\mathcal {V}$
is connected.
For this, replacing K by its finite extension, we may assume that there exist
![]() $a,b\in \mathcal {O}_{K}$
satisfying
$a,b\in \mathcal {O}_{K}$
satisfying
![]() $v_{p}(a)=v$
and
$v_{p}(a)=v$
and
![]() $v_{p}(b)=w$
. Consider the ring
$v_{p}(b)=w$
. Consider the ring
with
 $f=\prod _{\beta \in \tau \left (\bar {P}\right )}T_{\beta }$
. Then
$f=\prod _{\beta \in \tau \left (\bar {P}\right )}T_{\beta }$
. Then
![]() $\mathcal {V}=\mathrm {Sp}(\mathfrak {R}[1/p])$
and the special fiber
$\mathcal {V}=\mathrm {Sp}(\mathfrak {R}[1/p])$
and the special fiber
is reduced and connected. Then Lemma 3.2 concludes the proof.
3.1.4 Canonical subgroups over moduli spaces
Let n be a positive integer. Let
 $\underline {v}=\left (v_{\beta }\right )_{\beta \in \mathbb {B}_{F}}$
be a g-tuple satisfying
$\underline {v}=\left (v_{\beta }\right )_{\beta \in \mathbb {B}_{F}}$
be a g-tuple satisfying
for any
![]() $\beta \in \mathbb {B}_{F}$
. Note that the
$\beta \in \mathbb {B}_{F}$
. Note that the
![]() $1/(p^{n}(p-1))$
th lower ramification subgroups can be patched into a rigid analytic family [Reference Hattori28, Lemma 5.6]. Let R be an object of
$1/(p^{n}(p-1))$
th lower ramification subgroups can be patched into a rigid analytic family [Reference Hattori28, Lemma 5.6]. Let R be an object of
![]() $\mathbf {NAdm}$
and put
$\mathbf {NAdm}$
and put
![]() $\mathcal {U}=\mathrm {Sp}(R[1/p])$
. Let
$\mathcal {U}=\mathrm {Sp}(R[1/p])$
. Let
 $\mathcal {U}\to \mathfrak {M}(\mu _{N}, \mathfrak {c})\left (\underline {v}\right )^{\mathrm {rig}}$
be any morphism of rigid analytic varieties over K. This defines an HBAV
$\mathcal {U}\to \mathfrak {M}(\mu _{N}, \mathfrak {c})\left (\underline {v}\right )^{\mathrm {rig}}$
be any morphism of rigid analytic varieties over K. This defines an HBAV
![]() $\bar {A}^{\mathrm {un}}\rvert _{R}$
over
$\bar {A}^{\mathrm {un}}\rvert _{R}$
over
![]() $\mathrm {Spec}(R)$
. For any rig-point
$\mathrm {Spec}(R)$
. For any rig-point
![]() $x\in \mathrm {Spec}(R)$
, we have the canonical subgroup
$x\in \mathrm {Spec}(R)$
, we have the canonical subgroup
 $\mathcal {C}_{n}\left (\left (\bar {A}^{\mathrm {un}}\rvert _{R}\right )_{x}\right )$
by [Reference Hattori29, Theorem 8.1]. [Reference Hattori29, Theorem 8.1(7)] implies that they can be patched into an admissible open
$\mathcal {C}_{n}\left (\left (\bar {A}^{\mathrm {un}}\rvert _{R}\right )_{x}\right )$
by [Reference Hattori29, Theorem 8.1]. [Reference Hattori29, Theorem 8.1(7)] implies that they can be patched into an admissible open
![]() $\mathcal {O}_{F}$
-submodule
$\mathcal {O}_{F}$
-submodule
![]() $C_{n}$
of
$C_{n}$
of
![]() $\bar {\mathcal {A}}^{\mathrm {un}}[p^{n}]\rvert _{\mathcal {U}}$
. By [Reference Andreatta, Iovita and Pilloni3, Proposition 4.1.3], it uniquely extends to a finite flat subgroup scheme
$\bar {\mathcal {A}}^{\mathrm {un}}[p^{n}]\rvert _{\mathcal {U}}$
. By [Reference Andreatta, Iovita and Pilloni3, Proposition 4.1.3], it uniquely extends to a finite flat subgroup scheme
![]() $\mathcal {C}_{n}$
of
$\mathcal {C}_{n}$
of
![]() $\bar {A}^{\mathrm {un}}\rvert _{R}$
over
$\bar {A}^{\mathrm {un}}\rvert _{R}$
over
![]() $ \mathrm {Spec}(R)$
. Since
$ \mathrm {Spec}(R)$
. Since
![]() $\mathcal {C}_{n}$
agrees with the scheme-theoretic closure of
$\mathcal {C}_{n}$
agrees with the scheme-theoretic closure of
![]() $C_{n}$
in
$C_{n}$
in
 $\left (\bar {A}^{\mathrm {un}}\rvert _{R}\right )[p^{n}]$
, we see that
$\left (\bar {A}^{\mathrm {un}}\rvert _{R}\right )[p^{n}]$
, we see that
![]() $\mathcal {C}_{n}$
is stable under the
$\mathcal {C}_{n}$
is stable under the
![]() $\mathcal {O}_{F}$
-action.
$\mathcal {O}_{F}$
-action.
On the other hand, on a formal open neighborhood
![]() $\mathfrak {U}$
of a point of the boundary satisfying
$\mathfrak {U}$
of a point of the boundary satisfying
![]() $\mathfrak {U}\subseteq \bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)$
, the unit component
$\mathfrak {U}\subseteq \bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)$
, the unit component
![]() $\bar {\mathfrak {A}}^{\mathrm {un}}[p^{n}]^{0}\rvert _{\mathfrak {U}}$
is quasi-finite and flat over
$\bar {\mathfrak {A}}^{\mathrm {un}}[p^{n}]^{0}\rvert _{\mathfrak {U}}$
is quasi-finite and flat over
![]() $\mathfrak {U}$
with constant degree on each fiber by [Reference Rapoport36, p. 297(ii)]. Thus it is finite and flat. Then by gluing along
$\mathfrak {U}$
with constant degree on each fiber by [Reference Rapoport36, p. 297(ii)]. Thus it is finite and flat. Then by gluing along
![]() $\mathfrak {M}(\mu _{N},\mathfrak {c})(0)$
, we obtain a finite flat formal subgroup scheme
$\mathfrak {M}(\mu _{N},\mathfrak {c})(0)$
, we obtain a finite flat formal subgroup scheme
![]() $\mathcal {C}_{n}$
of
$\mathcal {C}_{n}$
of
![]() $\bar {\mathfrak {A}}^{\mathrm {un}}$
over
$\bar {\mathfrak {A}}^{\mathrm {un}}$
over
![]() $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
and its generic fiber
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
and its generic fiber
![]() $C_{n}$
, which we refer to as the canonical subgroup of level n.
$C_{n}$
, which we refer to as the canonical subgroup of level n.
Let R be a topological
![]() $\mathcal {O}_{K}$
-algebra which is quasi-idyllic with respect to the p-adic topology [Reference Abbes1, 1.10.1.1]. Since any finitely generated R-module is automatically p-adically complete [Reference Abbes1, Proposition 1.10.2], any finitely presented flat formal group scheme over
$\mathcal {O}_{K}$
-algebra which is quasi-idyllic with respect to the p-adic topology [Reference Abbes1, 1.10.1.1]. Since any finitely generated R-module is automatically p-adically complete [Reference Abbes1, Proposition 1.10.2], any finitely presented flat formal group scheme over
![]() $\mathrm {Spf}(R)$
can be identified with a finitely presented flat group scheme over
$\mathrm {Spf}(R)$
can be identified with a finitely presented flat group scheme over
![]() $\mathrm {Spec}(R)$
. Thus we have a theory of Cartier duality for any finitely presented flat formal group scheme
$\mathrm {Spec}(R)$
. Thus we have a theory of Cartier duality for any finitely presented flat formal group scheme
![]() $\mathcal {G}$
over any quasi-idyllic p-adic formal scheme, and we can define the Hodge–Tate map
$\mathcal {G}$
over any quasi-idyllic p-adic formal scheme, and we can define the Hodge–Tate map
 $$ \begin{align*} \mathrm{HT}_{\mathcal{G}}:\mathcal{G}(R)\to \omega_{\mathcal{G}^{\vee}},\quad x\mapsto x^{*}\left(\frac{dT}{T}\right). \end{align*} $$
$$ \begin{align*} \mathrm{HT}_{\mathcal{G}}:\mathcal{G}(R)\to \omega_{\mathcal{G}^{\vee}},\quad x\mapsto x^{*}\left(\frac{dT}{T}\right). \end{align*} $$
From the construction, we see that the restriction of the Cartier dual
 $\mathcal {C}_{n}^{\vee }\rvert _{\bar {\mathfrak {M}}\left (\mu _{N},\mathfrak {c}\right )(0)}$
to the ordinary locus is finite and étale.
$\mathcal {C}_{n}^{\vee }\rvert _{\bar {\mathfrak {M}}\left (\mu _{N},\mathfrak {c}\right )(0)}$
to the ordinary locus is finite and étale.
Note that for the function
 $$ \begin{align*} \delta_{K}(v)=\min\left([v/(p-1),+\infty)\cap e^{-1}\mathbb{Z}\right), \end{align*} $$
$$ \begin{align*} \delta_{K}(v)=\min\left([v/(p-1),+\infty)\cap e^{-1}\mathbb{Z}\right), \end{align*} $$
the ideal
 $m_{K}^{\geqslant v/(p-1)}$
is generated by
$m_{K}^{\geqslant v/(p-1)}$
is generated by
 $\pi _{K}^{e\delta _{K}(v)}$
. Then we have the following variant of [Reference Andreatta, Iovita and Pilloni3, Propositions 4.2.1 and 4.2.2]:
$\pi _{K}^{e\delta _{K}(v)}$
. Then we have the following variant of [Reference Andreatta, Iovita and Pilloni3, Propositions 4.2.1 and 4.2.2]:
Lemma 3.5. Let
 $\underline {v}=\left (v_{\beta }\right )_{\beta \in \mathbb {B}_{F}}$
be a g-tuple of nonnegative rational numbers satisfying
$\underline {v}=\left (v_{\beta }\right )_{\beta \in \mathbb {B}_{F}}$
be a g-tuple of nonnegative rational numbers satisfying
Let R be an object of
![]() $\mathbf {NAdm}$
. For any morphism of admissible formal schemes
$\mathbf {NAdm}$
. For any morphism of admissible formal schemes
 $\hat {f}:\mathrm {Spf}(R)\to \bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
over
$\hat {f}:\mathrm {Spf}(R)\to \bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
over
![]() $\mathcal {O}_{K}$
, consider the pullback
$\mathcal {O}_{K}$
, consider the pullback
![]() $G=\bar {A}^{\mathrm {un}}\rvert _{R}$
by the unique algebraization
$G=\bar {A}^{\mathrm {un}}\rvert _{R}$
by the unique algebraization
![]() $\mathrm {Spec}(R)\to \bar {M}(\mu _{N},\mathfrak {c})$
of
$\mathrm {Spec}(R)\to \bar {M}(\mu _{N},\mathfrak {c})$
of
![]() $\hat {f}$
and
$\hat {f}$
and
![]() $\mathcal {H}_{n}=\mathcal {C}_{n}\rvert _{\mathrm {Spf}(R)}$
, which is a subgroup scheme of the formal completion of G.
$\mathcal {H}_{n}=\mathcal {C}_{n}\rvert _{\mathrm {Spf}(R)}$
, which is a subgroup scheme of the formal completion of G.
-
(1) For any rational number
 $i\in e^{-1}\mathbb {Z}_{\geq 0}$
satisfying
$i\in e^{-1}\mathbb {Z}_{\geq 0}$
satisfying
 $i\leq n-v(p^{n}-1)/(p-1)$
, the natural map
$i\leq n-v(p^{n}-1)/(p-1)$
, the natural map
 $\omega _{G}\otimes _{\mathcal {O}_{K}} \mathcal {O}_{K,i}\to \omega _{\mathcal {H}_{n}} \otimes _{\mathcal {O}_{K}} \mathcal {O}_{K,i}$
is an isomorphism.
$\omega _{G}\otimes _{\mathcal {O}_{K}} \mathcal {O}_{K,i}\to \omega _{\mathcal {H}_{n}} \otimes _{\mathcal {O}_{K}} \mathcal {O}_{K,i}$
is an isomorphism. -
(2) Assume that we have an isomorphism of
 $\mathcal {O}_{F}$
-modules
$\mathcal {O}_{F}$
-modules
 $\mathcal {H}_{n}^{\vee }(R)\simeq \mathcal {O}_{F} /p^{n}\mathcal {O}_{F}$
. If there exists a rational number
$\mathcal {H}_{n}^{\vee }(R)\simeq \mathcal {O}_{F} /p^{n}\mathcal {O}_{F}$
. If there exists a rational number
 $i\in e^{-1}\mathbb {Z}_{\geq 0}$
satisfying
$i\in e^{-1}\mathbb {Z}_{\geq 0}$
satisfying
 $\delta _{K}(v)<i\leq n-v(p^{n}-1)/(p-1)$
, then the cokernel of the linearization of the Hodge–Tate map is killed by
$\delta _{K}(v)<i\leq n-v(p^{n}-1)/(p-1)$
, then the cokernel of the linearization of the Hodge–Tate map is killed by $$ \begin{align*} \mathrm{HT}_{\mathcal{H}^{\vee}_{n}}\otimes 1: \mathcal{H}_{n}^{\vee}(R)\otimes R\to \omega_{\mathcal{H}_{n}} \end{align*} $$
$$ \begin{align*} \mathrm{HT}_{\mathcal{H}^{\vee}_{n}}\otimes 1: \mathcal{H}_{n}^{\vee}(R)\otimes R\to \omega_{\mathcal{H}_{n}} \end{align*} $$
 $m_{K}^{\geqslant v/(p-1)}$
.
$m_{K}^{\geqslant v/(p-1)}$
.
Proof. Since the ordinary case is trivial, by a gluing argument we may assume that
![]() $\hat {f}$
factors through
$\hat {f}$
factors through
![]() $\mathfrak {M}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
. By replacing
$\mathfrak {M}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
. By replacing
![]() $\mathrm {Spf}(R)$
with its formal affine open subscheme, we may assume that R is an integral domain and
$\mathrm {Spf}(R)$
with its formal affine open subscheme, we may assume that R is an integral domain and
![]() $\omega _{G}$
is a free
$\omega _{G}$
is a free
![]() $\mathcal {O}_{F}\otimes R$
-module of rank
$\mathcal {O}_{F}\otimes R$
-module of rank
![]() $1$
. The first assertion follows by reducing it to [Reference Hattori29, Theorem 8.1(8)] in the same way as [Reference Andreatta, Iovita and Pilloni3, Proposition 4.2.1]. For the second assertion, take surjections
$1$
. The first assertion follows by reducing it to [Reference Hattori29, Theorem 8.1(8)] in the same way as [Reference Andreatta, Iovita and Pilloni3, Proposition 4.2.1]. For the second assertion, take surjections
![]() $R^{g} \to \mathcal {H}_{n}^{\vee }(R)\otimes R \simeq (R/p^{n} R)^{g}$
and
$R^{g} \to \mathcal {H}_{n}^{\vee }(R)\otimes R \simeq (R/p^{n} R)^{g}$
and
![]() $R^{g}\simeq \omega _{G}\to \omega _{\mathcal {H}_{n}}$
. Then the map
$R^{g}\simeq \omega _{G}\to \omega _{\mathcal {H}_{n}}$
. Then the map
![]() $\mathrm {HT}_{\mathcal {H}^{\vee }_{n}} \otimes 1$
can be identified with the reduction of the map defined by some matrix
$\mathrm {HT}_{\mathcal {H}^{\vee }_{n}} \otimes 1$
can be identified with the reduction of the map defined by some matrix
![]() $\gamma \in M_{g}(R)$
. It suffices to show
$\gamma \in M_{g}(R)$
. It suffices to show
 $m_{K}^{\geqslant v/(p-1)} R^{g}\subseteq \gamma (R^{g})$
. Let
$m_{K}^{\geqslant v/(p-1)} R^{g}\subseteq \gamma (R^{g})$
. Let
![]() $\mathfrak {p}$
be a prime ideal of R of height
$\mathfrak {p}$
be a prime ideal of R of height
![]() $1$
and let
$1$
and let
![]() $\hat {R}_{\mathfrak {p}}$
be the completion of the local ring
$\hat {R}_{\mathfrak {p}}$
be the completion of the local ring
![]() $R_{\mathfrak {p}}$
. [Reference Hattori29, Theorem 8.1(9)] implies
$R_{\mathfrak {p}}$
. [Reference Hattori29, Theorem 8.1(9)] implies
 $m_{K}^{\geqslant v/(p-1)} \hat {R}_{\mathfrak {p}}^{g}\subseteq \gamma \left (\hat {R}_{\mathfrak {p}}^{g}\right )+\pi _{K}^{e i}\hat {R}_{\mathfrak {p}}^{g}$
and thus
$m_{K}^{\geqslant v/(p-1)} \hat {R}_{\mathfrak {p}}^{g}\subseteq \gamma \left (\hat {R}_{\mathfrak {p}}^{g}\right )+\pi _{K}^{e i}\hat {R}_{\mathfrak {p}}^{g}$
and thus
 $m_{K}^{\geqslant v/(p-1)} \hat {R}_{\mathfrak {p}}^{g}\subseteq \gamma \left (\hat {R}_{\mathfrak {p}}^{g}\right )$
. This shows
$m_{K}^{\geqslant v/(p-1)} \hat {R}_{\mathfrak {p}}^{g}\subseteq \gamma \left (\hat {R}_{\mathfrak {p}}^{g}\right )$
. This shows
 $m_{K}^{\geqslant v/(p-1)} R_{\mathfrak {p}}^{g}\subseteq \gamma \left (R_{\mathfrak {p}}^{g}\right )$
and
$m_{K}^{\geqslant v/(p-1)} R_{\mathfrak {p}}^{g}\subseteq \gamma \left (R_{\mathfrak {p}}^{g}\right )$
and
![]() $\det (\gamma )\neq 0$
. Since R is normal,
$\det (\gamma )\neq 0$
. Since R is normal,
![]() $\gamma (R^{g})$
is the intersection of
$\gamma (R^{g})$
is the intersection of
 $\gamma \left (R_{\mathfrak {p}}^{g}\right )$
for every such
$\gamma \left (R_{\mathfrak {p}}^{g}\right )$
for every such
![]() $\mathfrak {p}$
, and the assertion follows.
$\mathfrak {p}$
, and the assertion follows.
3.2 Connected neighborhoods of critical points
Let
![]() $Y_{\mathfrak {c},p}$
be the moduli scheme parametrizing the isomorphism classes of pairs
$Y_{\mathfrak {c},p}$
be the moduli scheme parametrizing the isomorphism classes of pairs
![]() $(A, \mathcal {H})$
over schemes
$(A, \mathcal {H})$
over schemes
![]() $S/\mathrm {Spec}(\mathcal {O}_{K})$
, where A is an HBAV over S with
$S/\mathrm {Spec}(\mathcal {O}_{K})$
, where A is an HBAV over S with
![]() $\mathfrak {c}$
-polarization and
$\mathfrak {c}$
-polarization and
![]() $\Gamma _{00}(N)$
-structure, and
$\Gamma _{00}(N)$
-structure, and
![]() $\mathcal {H}$
is a finite locally free closed
$\mathcal {H}$
is a finite locally free closed
![]() $\mathcal {O}_{F}$
-subgroup scheme of
$\mathcal {O}_{F}$
-subgroup scheme of
![]() $A[p]$
of rank
$A[p]$
of rank
![]() $p^{g}$
over S such that
$p^{g}$
over S such that
![]() $\mathcal {H}$
is isotropic in the sense of [Reference Goren and Kassaei27, §2.1]. Then
$\mathcal {H}$
is isotropic in the sense of [Reference Goren and Kassaei27, §2.1]. Then
![]() $Y_{\mathfrak {c},p}$
is projective over
$Y_{\mathfrak {c},p}$
is projective over
![]() $M(\mu _{N},\mathfrak {c})$
[Reference Stamm38, p. 415]. For
$M(\mu _{N},\mathfrak {c})$
[Reference Stamm38, p. 415]. For
![]() $S=\mathrm {Spec}(\mathcal {O}_{L})$
with some extension
$S=\mathrm {Spec}(\mathcal {O}_{L})$
with some extension
![]() $L/K$
of complete valuation fields and an ideal
$L/K$
of complete valuation fields and an ideal
![]() $\mathfrak {a}$
of
$\mathfrak {a}$
of
![]() $\mathcal {O}_{F}$
, we say that
$\mathcal {O}_{F}$
, we say that
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $\mathfrak {a}$
-cyclic if the
$\mathfrak {a}$
-cyclic if the
![]() $\mathcal {O}_{F}$
-module
$\mathcal {O}_{F}$
-module
![]() $\mathcal {H}\left (\mathcal {O}_{\bar {L}}\right )$
is isomorphic to
$\mathcal {H}\left (\mathcal {O}_{\bar {L}}\right )$
is isomorphic to
![]() $\mathcal {O}_{F}/\mathfrak {a}$
, where
$\mathcal {O}_{F}/\mathfrak {a}$
, where
![]() $\bar {L}$
is an algebraic closure of L. Then
$\bar {L}$
is an algebraic closure of L. Then
![]() $\mathcal {H}$
is isotropic in this sense if and only if
$\mathcal {H}$
is isotropic in this sense if and only if
![]() $\mathcal {H}$
is p-cyclic.
$\mathcal {H}$
is p-cyclic.
Let
![]() $\mathfrak {Y}_{\mathfrak {c},p}$
be the p-adic formal completion of
$\mathfrak {Y}_{\mathfrak {c},p}$
be the p-adic formal completion of
![]() $Y_{\mathfrak {c},p}$
and let
$Y_{\mathfrak {c},p}$
and let
![]() $\mathcal {Y}_{\mathfrak {c},p}$
be its Raynaud generic fiber. Note that they are separated. By [Reference Rapoport36, Lemme 3.1], we have
$\mathcal {Y}_{\mathfrak {c},p}$
be its Raynaud generic fiber. Note that they are separated. By [Reference Rapoport36, Lemme 3.1], we have
![]() $\mathcal {Y}_{\mathfrak {c},p}(L)=\mathfrak {Y}_{\mathfrak {c},p}(\mathcal {O}_{L})=Y_{\mathfrak {c},p}(\mathcal {O}_{L})$
for any extension
$\mathcal {Y}_{\mathfrak {c},p}(L)=\mathfrak {Y}_{\mathfrak {c},p}(\mathcal {O}_{L})=Y_{\mathfrak {c},p}(\mathcal {O}_{L})$
for any extension
![]() $L/K$
of complete discrete valuation fields. In this subsection, we construct a connected admissible affinoid open neighborhood of a point
$L/K$
of complete discrete valuation fields. In this subsection, we construct a connected admissible affinoid open neighborhood of a point
![]() $Q=[(A,\mathcal {H})]$
of
$Q=[(A,\mathcal {H})]$
of
![]() $\mathcal {Y}_{\mathfrak {c},p}$
satisfying
$\mathcal {Y}_{\mathfrak {c},p}$
satisfying
![]() $\mathrm {Hdg}_{\beta }(A)=p/(p+1)$
for any
$\mathrm {Hdg}_{\beta }(A)=p/(p+1)$
for any
![]() $\beta \in \mathbb {B}_{F}$
inside the base extension
$\beta \in \mathbb {B}_{F}$
inside the base extension
 $\mathcal {Y}_{\mathfrak {c},p,\mathbb {C}_{p}}=\mathcal {Y}_{\mathfrak {c},p}\hat {\otimes }_{K} \mathbb {C}_{p}$
, assuming
$\mathcal {Y}_{\mathfrak {c},p,\mathbb {C}_{p}}=\mathcal {Y}_{\mathfrak {c},p}\hat {\otimes }_{K} \mathbb {C}_{p}$
, assuming
![]() $f_{\mathfrak {p}}\leq 2$
for any
$f_{\mathfrak {p}}\leq 2$
for any
![]() $\mathfrak {p}\mid p$
.
$\mathfrak {p}\mid p$
.
Lemma 3.6. There exists a point of
![]() $\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})$
corresponding to an HBAV A over the ring of integers
$\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})$
corresponding to an HBAV A over the ring of integers
![]() $\mathcal {O}_{L}$
of a finite extension
$\mathcal {O}_{L}$
of a finite extension
![]() $L/K$
satisfying
$L/K$
satisfying
![]() $ \mathrm {Hdg}_{\beta }(A)=p/(p+1)$
for any
$ \mathrm {Hdg}_{\beta }(A)=p/(p+1)$
for any
![]() $\beta \in \mathbb {B}_{F}$
.
$\beta \in \mathbb {B}_{F}$
.
Proof. Consider the stratum
![]() $W_{\mathbb {B}_{F}}$
of the special fiber
$W_{\mathbb {B}_{F}}$
of the special fiber
![]() $M(\mu _{N},\mathfrak {c})_{k}$
as in [Reference Goren and Kassaei27, §2.5]. Since
$M(\mu _{N},\mathfrak {c})_{k}$
as in [Reference Goren and Kassaei27, §2.5]. Since
![]() $W_{\mathbb {B}_{F}}$
is nonempty, there exists a point
$W_{\mathbb {B}_{F}}$
is nonempty, there exists a point
![]() $P\in \bar {\mathcal {M}}(\mu _{N},\mathfrak {c})$
such that
$P\in \bar {\mathcal {M}}(\mu _{N},\mathfrak {c})$
such that
![]() $\bar {P}=\mathrm {sp}(P)\in W_{\mathbb {B}_{F}}$
for the specialization map
$\bar {P}=\mathrm {sp}(P)\in W_{\mathbb {B}_{F}}$
for the specialization map
![]() $\mathrm {sp}: \bar {\mathcal {M}}(\mu _{N},\mathfrak {c})\to \bar {M}(\mu _{N},\mathfrak {c})_{k}$
as before. Since
$\mathrm {sp}: \bar {\mathcal {M}}(\mu _{N},\mathfrak {c})\to \bar {M}(\mu _{N},\mathfrak {c})_{k}$
as before. Since
![]() $\tau (\bar {P})=\mathbb {B}_{F}$
, the identifications (3.2) and (3.3) yield the lemma.
$\tau (\bar {P})=\mathbb {B}_{F}$
, the identifications (3.2) and (3.3) yield the lemma.
Proposition 3.7. Suppose
![]() $f_{\mathfrak {p}}\leq 2$
for any
$f_{\mathfrak {p}}\leq 2$
for any
![]() $\mathfrak {p}\mid p$
. Let
$\mathfrak {p}\mid p$
. Let
![]() $L/K$
be a finite extension in
$L/K$
be a finite extension in
![]() $\bar {\mathbb {Q}}_{p}$
and let l be the residue field of L. Let
$\bar {\mathbb {Q}}_{p}$
and let l be the residue field of L. Let
![]() $K^{\prime }$
be the composite field of K and
$K^{\prime }$
be the composite field of K and
![]() $\mathrm {Frac}(W(l))$
in
$\mathrm {Frac}(W(l))$
in
![]() $\bar {\mathbb {Q}}_{p}$
. Let
$\bar {\mathbb {Q}}_{p}$
. Let
![]() $[(A,\mathcal {H})]$
be an element of
$[(A,\mathcal {H})]$
be an element of
![]() $Y_{\mathfrak {c},p}(\mathcal {O}_{L})$
satisfying
$Y_{\mathfrak {c},p}(\mathcal {O}_{L})$
satisfying
![]() $\mathrm {Hdg}_{\beta }(A)=p/(p+1)$
for any
$\mathrm {Hdg}_{\beta }(A)=p/(p+1)$
for any
![]() $\beta \in \mathbb {B}_{F}$
, and let Q be the element of
$\beta \in \mathbb {B}_{F}$
, and let Q be the element of
![]() $\mathcal {Y}_{\mathfrak {c},p}(L)$
it defines. Let
$\mathcal {Y}_{\mathfrak {c},p}(L)$
it defines. Let
be the specialization map with respect to
![]() $\mathfrak {Y}_{\mathfrak {c},p}$
and put
$\mathfrak {Y}_{\mathfrak {c},p}$
and put
![]() $\bar {Q}=\mathrm {sp}(Q)$
. We define
$\bar {Q}=\mathrm {sp}(Q)$
. We define
 $$ \begin{align*} &\mathcal{V}_{\mathfrak{c},Q}=\left\{Q^{\prime}=[(A^{\prime},\mathcal{H}^{\prime})] \in \mathrm{sp}^{-1}\left(\bar{Q}\right) \ \middle|\ \frac{1}{p+1}\leq\deg_{\beta}(A'[p]/\mathcal{H}^{\prime})\leq \frac{p}{p+1},\right. \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\left.\mathrm{Hdg}_{\beta}(A^{\prime})\leq \frac{p}{p+1}\text{ for any }\beta\in \mathbb{B}_{F}\right\}, \end{align*} $$
$$ \begin{align*} &\mathcal{V}_{\mathfrak{c},Q}=\left\{Q^{\prime}=[(A^{\prime},\mathcal{H}^{\prime})] \in \mathrm{sp}^{-1}\left(\bar{Q}\right) \ \middle|\ \frac{1}{p+1}\leq\deg_{\beta}(A'[p]/\mathcal{H}^{\prime})\leq \frac{p}{p+1},\right. \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\left.\mathrm{Hdg}_{\beta}(A^{\prime})\leq \frac{p}{p+1}\text{ for any }\beta\in \mathbb{B}_{F}\right\}, \end{align*} $$
 $$ \begin{align*} \mathcal{V}_{\mathfrak{c},Q}\left(\tfrac{1}{p+1}\right)=\left\{Q^{\prime}=[(A^{\prime},\mathcal{H}^{\prime})] \in \mathcal{V}_{\mathfrak{c},Q}\ \middle|\ \deg_{\beta}(A^{\prime}[p]/\mathcal{H}^{\prime})\leq \frac{1}{p+1}\text{ for any }\beta\in \mathbb{B}_{F}\right\}. \end{align*} $$
$$ \begin{align*} \mathcal{V}_{\mathfrak{c},Q}\left(\tfrac{1}{p+1}\right)=\left\{Q^{\prime}=[(A^{\prime},\mathcal{H}^{\prime})] \in \mathcal{V}_{\mathfrak{c},Q}\ \middle|\ \deg_{\beta}(A^{\prime}[p]/\mathcal{H}^{\prime})\leq \frac{1}{p+1}\text{ for any }\beta\in \mathbb{B}_{F}\right\}. \end{align*} $$
Then they are admissible affinoid open subsets of
![]() $\mathcal {Y}_{\mathfrak {c},p}$
defined over
$\mathcal {Y}_{\mathfrak {c},p}$
defined over
![]() $K^{\prime }$
such that
$K^{\prime }$
such that
![]() $\mathcal {V}_{\mathfrak {c},Q}\hat {\otimes }_{K^{\prime }}\mathbb {C}_{p}$
is connected.
$\mathcal {V}_{\mathfrak {c},Q}\hat {\otimes }_{K^{\prime }}\mathbb {C}_{p}$
is connected.
Proof. By the assumption
![]() $f_{\mathfrak {p}}\leq 2$
and [Reference Hattori29, Proposition 6.1], we have the equality
$f_{\mathfrak {p}}\leq 2$
and [Reference Hattori29, Proposition 6.1], we have the equality
![]() $\deg _{\beta }(A[p]/\mathcal {H})=p/(p+1)$
for any
$\deg _{\beta }(A[p]/\mathcal {H})=p/(p+1)$
for any
![]() $\beta \in \mathbb {B}_{F}$
. [Reference Tian39, Proposition 4.2] shows that this value is equal to the one denoted by
$\beta \in \mathbb {B}_{F}$
. [Reference Tian39, Proposition 4.2] shows that this value is equal to the one denoted by
![]() $\nu _{\beta }(Q)$
in [Reference Goren and Kassaei27, §4.2]. In particular, the definition of
$\nu _{\beta }(Q)$
in [Reference Goren and Kassaei27, §4.2]. In particular, the definition of
![]() $\nu _{\beta }(Q)$
in [Reference Goren and Kassaei27, §4.2] implies
$\nu _{\beta }(Q)$
in [Reference Goren and Kassaei27, §4.2] implies
 $I\left (\bar {Q}\right )=\mathbb {B}_{F}$
with the notation of [Reference Goren and Kassaei27, (2.3.2)].
$I\left (\bar {Q}\right )=\mathbb {B}_{F}$
with the notation of [Reference Goren and Kassaei27, (2.3.2)].
We claim that the complete local ring
 $\hat {\mathcal {O}}_{Y_{\mathfrak {c},p},\bar {Q}}$
of
$\hat {\mathcal {O}}_{Y_{\mathfrak {c},p},\bar {Q}}$
of
![]() $Y_{\mathfrak {c},p}$
at
$Y_{\mathfrak {c},p}$
at
![]() $\bar {Q}$
is isomorphic to the ring
$\bar {Q}$
is isomorphic to the ring
and that there exists
![]() $g_{\beta }\in (\mathfrak {B}^{\prime })^{\times }$
such that for any finite extension
$g_{\beta }\in (\mathfrak {B}^{\prime })^{\times }$
such that for any finite extension
![]() $E/K^{\prime }$
and any
$E/K^{\prime }$
and any
![]() $\mathcal {O}_{K^{\prime }}$
-algebra homomorphism
$\mathcal {O}_{K^{\prime }}$
-algebra homomorphism
![]() $x: \mathfrak {B}^{\prime }\to \mathcal {O}_{E}$
, the corresponding
$x: \mathfrak {B}^{\prime }\to \mathcal {O}_{E}$
, the corresponding
![]() $\mathcal {O}_{E}$
-valued point
$\mathcal {O}_{E}$
-valued point
![]() $[(A^{\prime },\mathcal {H}^{\prime })]$
of
$[(A^{\prime },\mathcal {H}^{\prime })]$
of
![]() $Y_{\mathfrak {c},p}$
satisfies
$Y_{\mathfrak {c},p}$
satisfies
 $$ \begin{align*} \deg_{\beta}(A^{\prime}[p]/\mathcal{H}^{\prime})=\min\{v_p(X_\beta(x)),1\},\qquad \mathrm{Hdg}_{\beta}(A^{\prime})=\min\{v_p((X_\beta+g_\beta Y^p_{\sigma^{-1}\circ\beta})(x)),1\}. \end{align*} $$
$$ \begin{align*} \deg_{\beta}(A^{\prime}[p]/\mathcal{H}^{\prime})=\min\{v_p(X_\beta(x)),1\},\qquad \mathrm{Hdg}_{\beta}(A^{\prime})=\min\{v_p((X_\beta+g_\beta Y^p_{\sigma^{-1}\circ\beta})(x)),1\}. \end{align*} $$
Indeed, let
![]() $Y_{\mathfrak {c}}$
be a moduli scheme over W similar to
$Y_{\mathfrak {c}}$
be a moduli scheme over W similar to
![]() $Y_{\mathfrak {c},p}$
considered in [Reference Goren and Kassaei27, §2.1]. Let R be the affine algebra of an affine open neighborhood of
$Y_{\mathfrak {c},p}$
considered in [Reference Goren and Kassaei27, §2.1]. Let R be the affine algebra of an affine open neighborhood of
![]() $\bar {Q}$
in
$\bar {Q}$
in
![]() $Y_{\mathfrak {c}}$
and let
$Y_{\mathfrak {c}}$
and let
![]() $m_{\bar {Q}}$
be the maximal ideal of R corresponding to
$m_{\bar {Q}}$
be the maximal ideal of R corresponding to
![]() $\bar {Q}$
. The ring
$\bar {Q}$
. The ring
 $\hat {\mathcal {O}}_{Y_{\mathfrak {c},p},\bar {Q}}$
is equal to the completion of the local ring of
$\hat {\mathcal {O}}_{Y_{\mathfrak {c},p},\bar {Q}}$
is equal to the completion of the local ring of
![]() $R\otimes _{W} \mathcal {O}_{K}$
at the kernel
$R\otimes _{W} \mathcal {O}_{K}$
at the kernel
![]() $n_{\bar {Q}}$
of the map
$n_{\bar {Q}}$
of the map
![]() $R\otimes _{W} \mathcal {O}_{K} \to l$
associated to
$R\otimes _{W} \mathcal {O}_{K} \to l$
associated to
![]() $m_{\bar {Q}}$
.
$m_{\bar {Q}}$
.
By Stamm’s theorem [Reference Stamm38] (see also [Reference Goren and Kassaei27, Theorem 2.4.1′]), the
![]() $m_{\bar {Q}}$
-adic completion
$m_{\bar {Q}}$
-adic completion
 $\hat {R}_{m_{\bar {Q}}}$
of the localization
$\hat {R}_{m_{\bar {Q}}}$
of the localization
![]() $R_{m_{\bar {Q}}}$
is isomorphic to the ring
$R_{m_{\bar {Q}}}$
is isomorphic to the ring
Moreover, since
![]() $\mathrm {Hdg}_{\beta }(A)\neq 0$
for any
$\mathrm {Hdg}_{\beta }(A)\neq 0$
for any
![]() $\beta \in \mathbb {B}_{F}$
, equation (3.3) implies
$\beta \in \mathbb {B}_{F}$
, equation (3.3) implies
 $\tau \left (\bar {Q}\right )=\mathbb {B}_{F}$
. Thus, for any finite extension
$\tau \left (\bar {Q}\right )=\mathbb {B}_{F}$
. Thus, for any finite extension
![]() $E/\mathrm {Frac}(W(l))$
and any
$E/\mathrm {Frac}(W(l))$
and any
![]() $W(l)$
-algebra homomorphism
$W(l)$
-algebra homomorphism
![]() $x:\mathfrak {B}\to \mathcal {O}_{E}$
, the corresponding HBAV
$x:\mathfrak {B}\to \mathcal {O}_{E}$
, the corresponding HBAV
![]() $A^{\prime }$
satisfies
$A^{\prime }$
satisfies
![]() $v\left (t_{\beta }(x)\right )=\mathrm {Hdg}_{\beta }(A^{\prime })$
. By [Reference Goren and Kassaei27, Lemma 2.8.1] and the definition of
$v\left (t_{\beta }(x)\right )=\mathrm {Hdg}_{\beta }(A^{\prime })$
. By [Reference Goren and Kassaei27, Lemma 2.8.1] and the definition of
![]() $\nu _{\beta }(Q)$
in [Reference Goren and Kassaei27, §4.2], the isomorphism
$\nu _{\beta }(Q)$
in [Reference Goren and Kassaei27, §4.2], the isomorphism
 $\hat {R}_{m_{\bar {Q}}}\simeq \mathfrak {B}$
gives an identification of
$\hat {R}_{m_{\bar {Q}}}\simeq \mathfrak {B}$
gives an identification of
![]() $\deg _{\beta }$
and
$\deg _{\beta }$
and
![]() $\mathrm {Hdg}_{\beta }$
for the ring
$\mathrm {Hdg}_{\beta }$
for the ring
![]() $\mathfrak {B}$
as claimed before. Then the claim follows from Lemma 3.3.
$\mathfrak {B}$
as claimed before. Then the claim follows from Lemma 3.3.
By [Reference de Jong19, Lemma 7.2.5], we have
 $$ \begin{align*} \mathrm{sp}^{-1}\left(\bar{Q}\right)=(\mathrm{Spf}(\mathfrak{B}^{\prime}))^{\mathrm{rig}}. \end{align*} $$
$$ \begin{align*} \mathrm{sp}^{-1}\left(\bar{Q}\right)=(\mathrm{Spf}(\mathfrak{B}^{\prime}))^{\mathrm{rig}}. \end{align*} $$
Thus
![]() $\mathcal {V}_{\mathfrak {c},Q}$
is the
$\mathcal {V}_{\mathfrak {c},Q}$
is the
![]() $K^{\prime }$
-affinoid variety whose affinoid ring is the quotient of the Tate algebra
$K^{\prime }$
-affinoid variety whose affinoid ring is the quotient of the Tate algebra
by the ideal generated by
 $$ \begin{align*} X_{\beta}^{p+1}-p U_{\beta},\quad X_{\beta}^{p+1} V_{\beta} - p^{p},\quad X_{\beta} Y_{\beta}-p,\quad W_{\beta}\left(X_{\beta} +g_{\beta} Y_{\sigma^{-1}\circ \beta}^{p}\right)^{p+1} - p^{p} \end{align*} $$
$$ \begin{align*} X_{\beta}^{p+1}-p U_{\beta},\quad X_{\beta}^{p+1} V_{\beta} - p^{p},\quad X_{\beta} Y_{\beta}-p,\quad W_{\beta}\left(X_{\beta} +g_{\beta} Y_{\sigma^{-1}\circ \beta}^{p}\right)^{p+1} - p^{p} \end{align*} $$
for any
![]() $\beta \in \mathbb {B}_{F}$
. From this, we also obtain a similar description of
$\beta \in \mathbb {B}_{F}$
. From this, we also obtain a similar description of
 $\mathcal {V}_{\mathfrak {c},Q}\left (\tfrac {1}{p+1}\right )$
as a
$\mathcal {V}_{\mathfrak {c},Q}\left (\tfrac {1}{p+1}\right )$
as a
![]() $K^{\prime }$
-affinoid variety.
$K^{\prime }$
-affinoid variety.
Next we prove that the base extension
![]() $\mathcal {V}_{\mathfrak {c},Q}\hat {\otimes }_{K^{\prime }} \mathbb {C}_{p}$
is connected. Put
$\mathcal {V}_{\mathfrak {c},Q}\hat {\otimes }_{K^{\prime }} \mathbb {C}_{p}$
is connected. Put
![]() $r=1/(p+1)$
and
$r=1/(p+1)$
and
![]() $s=p/(p+1)$
. Fix a
$s=p/(p+1)$
. Fix a
![]() $(p+1)$
th root
$(p+1)$
th root
![]() $\varpi =p^{1/ (p+1)}$
of p in
$\varpi =p^{1/ (p+1)}$
of p in
![]() $\bar {\mathbb {Q}}_{p}$
. Then the affinoid ring
$\bar {\mathbb {Q}}_{p}$
. Then the affinoid ring
![]() $B_{Q,\mathbb {C}_{p}}$
of
$B_{Q,\mathbb {C}_{p}}$
of
![]() $\mathcal {V}_{\mathfrak {c},Q}\hat {\otimes }_{K^{\prime }} \mathbb {C}_{p}$
is also isomorphic to the quotient of the Tate algebra
$\mathcal {V}_{\mathfrak {c},Q}\hat {\otimes }_{K^{\prime }} \mathbb {C}_{p}$
is also isomorphic to the quotient of the Tate algebra
by the ideal generated by
 $$ \begin{align*} X_{\beta}-\varpi U_{\beta},\quad X_{\beta} V_{\beta} - \varpi^{p},\quad X_{\beta} Y_{\beta}-\varpi^{p+1},\quad W_{\beta}\left(X_{\beta} +g_{\beta} Y_{\sigma^{-1}\circ \beta}^{p}\right) - \varpi^{p} \end{align*} $$
$$ \begin{align*} X_{\beta}-\varpi U_{\beta},\quad X_{\beta} V_{\beta} - \varpi^{p},\quad X_{\beta} Y_{\beta}-\varpi^{p+1},\quad W_{\beta}\left(X_{\beta} +g_{\beta} Y_{\sigma^{-1}\circ \beta}^{p}\right) - \varpi^{p} \end{align*} $$
for any
![]() $\beta \in \mathbb {B}_{F}$
. Note that in the ring
$\beta \in \mathbb {B}_{F}$
. Note that in the ring
![]() $B_{Q,\mathbb {C}_{p}}$
we also have
$B_{Q,\mathbb {C}_{p}}$
we also have
![]() $Y_{\beta }-\varpi V_{\beta }=0$
. Hence
$Y_{\beta }-\varpi V_{\beta }=0$
. Hence
![]() $B_{Q,\mathbb {C}_{p}}$
is isomorphic to the quotient of the ring
$B_{Q,\mathbb {C}_{p}}$
is isomorphic to the quotient of the ring
by the ideal generated by
 $$ \begin{align*} U_{\beta} V_{\beta} -\varpi^{p-1},\quad F_{\beta}:=W_{\beta}\left(U_{\beta}+\varpi^{p-1} g^{\prime}_{\beta} V_{\sigma^{-1}\circ \beta}^{p}\right)-\varpi^{p-1} \end{align*} $$
$$ \begin{align*} U_{\beta} V_{\beta} -\varpi^{p-1},\quad F_{\beta}:=W_{\beta}\left(U_{\beta}+\varpi^{p-1} g^{\prime}_{\beta} V_{\sigma^{-1}\circ \beta}^{p}\right)-\varpi^{p-1} \end{align*} $$
for any
![]() $\beta \in \mathbb {B}_{F}$
with some
$\beta \in \mathbb {B}_{F}$
with some
 $g^{\prime }_{\beta }\in \mathfrak {A}_{Q,\mathbb {C}_{p}}^{\times }$
, where
$g^{\prime }_{\beta }\in \mathfrak {A}_{Q,\mathbb {C}_{p}}^{\times }$
, where
 $$ \begin{align*} \mathfrak{A}_{Q,\mathbb{C}_{p}}=\mathcal{O}_{\mathbb{C}_{p}}\left\langle U_{\beta},V_{\beta}\mid \beta\in \mathbb{B}_{F}\right\rangle/\left(U_{\beta} V_{\beta}-\varpi^{p-1}\mid \beta\in \mathbb{B}_{F}\right). \end{align*} $$
$$ \begin{align*} \mathfrak{A}_{Q,\mathbb{C}_{p}}=\mathcal{O}_{\mathbb{C}_{p}}\left\langle U_{\beta},V_{\beta}\mid \beta\in \mathbb{B}_{F}\right\rangle/\left(U_{\beta} V_{\beta}-\varpi^{p-1}\mid \beta\in \mathbb{B}_{F}\right). \end{align*} $$
From these equations, we see that
 $$ \begin{align*} G_{\beta}:=V_{\beta}-W_{\beta}\left(1+g^{\prime}_{\beta} V_{\beta} V_{\sigma^{-1}\circ \beta}^{p}\right)=0 \end{align*} $$
$$ \begin{align*} G_{\beta}:=V_{\beta}-W_{\beta}\left(1+g^{\prime}_{\beta} V_{\beta} V_{\sigma^{-1}\circ \beta}^{p}\right)=0 \end{align*} $$
in this quotient. Since
we obtain
 $$ \begin{align*} B_{Q,\mathbb{C}_{p}}\simeq \mathbb{C}_{p}\left\langle U_{\beta}, V_{\beta}, W_{\beta}\mid \beta\in \mathbb{B}_{F}\right\rangle/\left(U_{\beta} V_{\beta}-\varpi^{p-1}, G_{\beta}\mid \beta\in \mathbb{B}_{F}\right). \end{align*} $$
$$ \begin{align*} B_{Q,\mathbb{C}_{p}}\simeq \mathbb{C}_{p}\left\langle U_{\beta}, V_{\beta}, W_{\beta}\mid \beta\in \mathbb{B}_{F}\right\rangle/\left(U_{\beta} V_{\beta}-\varpi^{p-1}, G_{\beta}\mid \beta\in \mathbb{B}_{F}\right). \end{align*} $$
Note that the ring
 $$ \begin{align*} \mathfrak{B}_{Q,\mathbb{C}_{p}}=\mathcal{O}_{\mathbb{C}_{p}}\left\langle U_{\beta}, V_{\beta}, W_{\beta} \mid \beta\in \mathbb{B}_{F}\right\rangle/\left(U_{\beta} V_{\beta}-\varpi^{p-1}, G_{\beta}\mid \beta\in \mathbb{B}_{F}\right) \end{align*} $$
$$ \begin{align*} \mathfrak{B}_{Q,\mathbb{C}_{p}}=\mathcal{O}_{\mathbb{C}_{p}}\left\langle U_{\beta}, V_{\beta}, W_{\beta} \mid \beta\in \mathbb{B}_{F}\right\rangle/\left(U_{\beta} V_{\beta}-\varpi^{p-1}, G_{\beta}\mid \beta\in \mathbb{B}_{F}\right) \end{align*} $$
is a flat
![]() $\mathcal {O}_{\mathbb {C}_{p}}$
-algebra. Indeed, consider the polynomial ring
$\mathcal {O}_{\mathbb {C}_{p}}$
-algebra. Indeed, consider the polynomial ring
![]() $\mathfrak {A}_{Q,\mathbb {C}_{p}}\left [W_{\beta }\right ]$
. Since the coefficients of
$\mathfrak {A}_{Q,\mathbb {C}_{p}}\left [W_{\beta }\right ]$
. Since the coefficients of
![]() $G_{\beta }$
as a polynomial of
$G_{\beta }$
as a polynomial of
![]() $W_{\beta }$
generate the unit ideal
$W_{\beta }$
generate the unit ideal
![]() $\mathfrak {A}_{Q,\mathbb {C}_{p}}$
, by a limit argument reducing to the Noetherian case and using [Reference Matsumura34, (20.F), Corollary 2] we see that the
$\mathfrak {A}_{Q,\mathbb {C}_{p}}$
, by a limit argument reducing to the Noetherian case and using [Reference Matsumura34, (20.F), Corollary 2] we see that the
![]() $\mathfrak {A}_{Q,\mathbb {C}_{p}}$
-algebra
$\mathfrak {A}_{Q,\mathbb {C}_{p}}$
-algebra
is flat. By [Reference Abbes1, Proposition 1.10.2(ii)], the p-adic completion of this algebra is
![]() $\mathfrak {B}_{Q,\mathbb {C}_{p}}$
. Since the
$\mathfrak {B}_{Q,\mathbb {C}_{p}}$
. Since the
![]() $\mathcal {O}_{\mathbb {C}_{p}}$
-algebra
$\mathcal {O}_{\mathbb {C}_{p}}$
-algebra
![]() $\mathfrak {A}_{Q,\mathbb {C}_{p}}$
is flat, the p-adic completion
$\mathfrak {A}_{Q,\mathbb {C}_{p}}$
is flat, the p-adic completion
![]() $\mathfrak {B}_{Q,\mathbb {C}_{p}}$
is also flat over
$\mathfrak {B}_{Q,\mathbb {C}_{p}}$
is also flat over
![]() $\mathcal {O}_{\mathbb {C}_{p}}$
.
$\mathcal {O}_{\mathbb {C}_{p}}$
.
Put
![]() $\bar {G}_{\beta }=G_{\beta } \bmod m_{\mathbb {C}_{p}}$
and
$\bar {G}_{\beta }=G_{\beta } \bmod m_{\mathbb {C}_{p}}$
and
 $$ \begin{align*} \bar{R}=\bar{\mathbb{F}}_{p} \left[U_{\beta}, V_{\beta}, W_{\beta}\mid \beta\in \mathbb{B}_{F}\right],\qquad \bar{J}=\left(U_{\beta} V_{\beta}, \bar{G}_{\beta}\mid \beta\in \mathbb{B}_{F}\right). \end{align*} $$
$$ \begin{align*} \bar{R}=\bar{\mathbb{F}}_{p} \left[U_{\beta}, V_{\beta}, W_{\beta}\mid \beta\in \mathbb{B}_{F}\right],\qquad \bar{J}=\left(U_{\beta} V_{\beta}, \bar{G}_{\beta}\mid \beta\in \mathbb{B}_{F}\right). \end{align*} $$
Next we claim that the reduction
 $\bar {\mathfrak {B}}_{Q,\mathbb {C}_{p}}=\bar {R}/\bar {J}$
of
$\bar {\mathfrak {B}}_{Q,\mathbb {C}_{p}}=\bar {R}/\bar {J}$
of
![]() $\mathfrak {B}_{Q,\mathbb {C}_{p}}$
is reduced and
$\mathfrak {B}_{Q,\mathbb {C}_{p}}$
is reduced and
 $\mathrm {Spec}\left (\bar {\mathfrak {B}}_{Q,\mathbb {C}_{p}}\right )$
is connected. For reducedness, it suffices to show that the localization at every maximal ideal is reduced. Let
$\mathrm {Spec}\left (\bar {\mathfrak {B}}_{Q,\mathbb {C}_{p}}\right )$
is connected. For reducedness, it suffices to show that the localization at every maximal ideal is reduced. Let
![]() $\mathfrak {M}$
be any maximal ideal of
$\mathfrak {M}$
be any maximal ideal of
![]() $\bar {R}$
containing
$\bar {R}$
containing
![]() $\bar {J}$
. Then we have
$\bar {J}$
. Then we have
 $$ \begin{align*} 1+g^{\prime}_{\beta} V_{\beta} V_{\sigma^{-1}\circ \beta}^{p} \notin \mathfrak{M}, \end{align*} $$
$$ \begin{align*} 1+g^{\prime}_{\beta} V_{\beta} V_{\sigma^{-1}\circ \beta}^{p} \notin \mathfrak{M}, \end{align*} $$
since, supposing the contrary,
![]() $\bar {G}_{\beta }\in \mathfrak {M}$
implies
$\bar {G}_{\beta }\in \mathfrak {M}$
implies
![]() $V_{\beta }\in \mathfrak {M}$
and
$V_{\beta }\in \mathfrak {M}$
and
![]() $1\in \mathfrak {M}$
, which is a contradiction. Thus in the ring
$1\in \mathfrak {M}$
, which is a contradiction. Thus in the ring
![]() $\bar {R}_{\mathfrak {M}}$
we have
$\bar {R}_{\mathfrak {M}}$
we have
 $$ \begin{align*} W_{\beta}-V_{\beta}\left(1+g^{\prime}_{\beta} V_{\beta} V_{\sigma^{-1}\circ \beta}^{p}\right)^{-1}\in \bar{J} \bar{R}_{\mathfrak{M}} \end{align*} $$
$$ \begin{align*} W_{\beta}-V_{\beta}\left(1+g^{\prime}_{\beta} V_{\beta} V_{\sigma^{-1}\circ \beta}^{p}\right)^{-1}\in \bar{J} \bar{R}_{\mathfrak{M}} \end{align*} $$
for any
![]() $\beta \in \mathbb {B}_{F}$
. Hence the localization
$\beta \in \mathbb {B}_{F}$
. Hence the localization
 $\left (\bar {\mathfrak {B}}_{Q,\mathbb {C}_{p}}\right )_{\mathfrak {M}}$
is isomorphic to the localization of the ring
$\left (\bar {\mathfrak {B}}_{Q,\mathbb {C}_{p}}\right )_{\mathfrak {M}}$
is isomorphic to the localization of the ring
at the pullback of
![]() $\mathfrak {M}$
, which is reduced.
$\mathfrak {M}$
, which is reduced.
Let us show the connectedness. Let
![]() $\mathbb {B}_{F}=\mathbb {B}_{U} \coprod \mathbb {B}_{V}$
be a decomposition into the disjoint union of two subsets. Consider the closed subscheme
$\mathbb {B}_{F}=\mathbb {B}_{U} \coprod \mathbb {B}_{V}$
be a decomposition into the disjoint union of two subsets. Consider the closed subscheme
![]() $F_{\mathbb {B}_{U},\mathbb {B}_{V}}$
of
$F_{\mathbb {B}_{U},\mathbb {B}_{V}}$
of
 $\mathrm {Spec}\left (\bar {\mathfrak {B}}_{Q,\mathbb {C}_{p}}\right )$
defined by
$\mathrm {Spec}\left (\bar {\mathfrak {B}}_{Q,\mathbb {C}_{p}}\right )$
defined by
![]() $U_{\beta }=0$
for
$U_{\beta }=0$
for
![]() $\beta \in \mathbb {B}_{U}$
and
$\beta \in \mathbb {B}_{U}$
and
![]() $V_{\beta }=0$
for
$V_{\beta }=0$
for
![]() $\beta \in \mathbb {B}_{V}$
. Since every
$\beta \in \mathbb {B}_{V}$
. Since every
![]() $F_{\mathbb {B}_{U},\mathbb {B}_{V}}$
contains the point defined by
$F_{\mathbb {B}_{U},\mathbb {B}_{V}}$
contains the point defined by
![]() $U_{\beta }=V_{\beta }=W_{\beta }=0$
for any
$U_{\beta }=V_{\beta }=W_{\beta }=0$
for any
![]() $\beta \in \mathbb {B}_{F}$
, it is enough to show that
$\beta \in \mathbb {B}_{F}$
, it is enough to show that
![]() $F_{\mathbb {B}_{U}, \mathbb {B}_{V}}$
is connected for any such decomposition of
$F_{\mathbb {B}_{U}, \mathbb {B}_{V}}$
is connected for any such decomposition of
![]() $\mathbb {B}_{F}$
. Put
$\mathbb {B}_{F}$
. Put
Note that the
![]() $\bar {\mathfrak {A}}_{\mathbb {B}_{U},\mathbb {B}_{V}}$
-algebra
$\bar {\mathfrak {A}}_{\mathbb {B}_{U},\mathbb {B}_{V}}$
-algebra
 $$ \begin{align*} \bar{\mathfrak{A}}_{\mathbb{B}_{U},\mathbb{B}_{V}}\left[W_{\beta}\mid \beta\in \mathbb{B}_{F}\right]/\left(\bar{G}_{\beta}\mid \beta\in \mathbb{B}_{F}\right) \end{align*} $$
$$ \begin{align*} \bar{\mathfrak{A}}_{\mathbb{B}_{U},\mathbb{B}_{V}}\left[W_{\beta}\mid \beta\in \mathbb{B}_{F}\right]/\left(\bar{G}_{\beta}\mid \beta\in \mathbb{B}_{F}\right) \end{align*} $$
is flat. From this we see that the affine algebra of
![]() $F_{\mathbb {B}_{U},\mathbb {B}_{V}}$
can be identified with the subring
$F_{\mathbb {B}_{U},\mathbb {B}_{V}}$
can be identified with the subring
 $$ \begin{align*} \bar{\mathfrak{A}}_{\mathbb{B}_{U},\mathbb{B}_{V}} \left[\frac{V_{\beta}}{1+g^{\prime}_{\beta} V_{\beta} V_{\sigma^{-1}\circ\beta}}\ \middle|\ \beta\in \mathbb{B}_{F}\right] \end{align*} $$
$$ \begin{align*} \bar{\mathfrak{A}}_{\mathbb{B}_{U},\mathbb{B}_{V}} \left[\frac{V_{\beta}}{1+g^{\prime}_{\beta} V_{\beta} V_{\sigma^{-1}\circ\beta}}\ \middle|\ \beta\in \mathbb{B}_{F}\right] \end{align*} $$
of
 $\mathrm {Frac}\left (\bar {\mathfrak {A}}_{\mathbb {B}_{U},\mathbb {B}_{V}}\right )$
, which is an integral domain. Hence we obtain the connectedness of
$\mathrm {Frac}\left (\bar {\mathfrak {A}}_{\mathbb {B}_{U},\mathbb {B}_{V}}\right )$
, which is an integral domain. Hence we obtain the connectedness of
 $\bar {\mathfrak {B}}_{Q,\mathbb {C}_{p}}$
. By [Reference de Jong19, Lemma 7.1.9],
$\bar {\mathfrak {B}}_{Q,\mathbb {C}_{p}}$
. By [Reference de Jong19, Lemma 7.1.9],
 $\mathrm {sp}^{-1}\left (\bar {Q}\right )$
is reduced, and [Reference Conrad17, Lemma 3.3.1(1)] shows that
$\mathrm {sp}^{-1}\left (\bar {Q}\right )$
is reduced, and [Reference Conrad17, Lemma 3.3.1(1)] shows that
![]() $\mathcal {V}_{\mathfrak {c},Q}\hat {\otimes }_{K^{\prime }} \mathbb {C}_{p}$
is also reduced. Then Lemma 3.2 shows that
$\mathcal {V}_{\mathfrak {c},Q}\hat {\otimes }_{K^{\prime }} \mathbb {C}_{p}$
is also reduced. Then Lemma 3.2 shows that
![]() $\mathcal {V}_{\mathfrak {c},Q}\hat {\otimes }_{K^{\prime }}\mathbb {C}_{p}$
is connected.
$\mathcal {V}_{\mathfrak {c},Q}\hat {\otimes }_{K^{\prime }}\mathbb {C}_{p}$
is connected.
Lemma 3.8. Suppose
![]() $f_{\mathfrak {p}}\leq 2$
for any
$f_{\mathfrak {p}}\leq 2$
for any
![]() $\mathfrak {p}\mid p$
. Let
$\mathfrak {p}\mid p$
. Let
![]() $L/K$
be a finite extension. Let
$L/K$
be a finite extension. Let
![]() $[(A,\mathcal {H})]$
be an element of
$[(A,\mathcal {H})]$
be an element of
![]() $Y_{\mathfrak {c},p}(\mathcal {O}_{L})$
satisfying
$Y_{\mathfrak {c},p}(\mathcal {O}_{L})$
satisfying
for any
![]() $\beta \in \mathbb {B}_{F}$
. Then for any
$\beta \in \mathbb {B}_{F}$
. Then for any
![]() $\mathfrak {p}\mid p$
, either
$\mathfrak {p}\mid p$
, either
![]() $A[p]_{\mathfrak {p}}$
has the canonical subgroup of level
$A[p]_{\mathfrak {p}}$
has the canonical subgroup of level
![]() $1$
which is equal to
$1$
which is equal to
![]() $\mathcal {H}_{\mathfrak {p}}$
, or
$\mathcal {H}_{\mathfrak {p}}$
, or
![]() $\mathrm {Hdg}_{\beta }(A)=p/(p+1)$
for any
$\mathrm {Hdg}_{\beta }(A)=p/(p+1)$
for any
![]() $\beta \in \mathbb {B}_{\mathfrak {p}}$
.
$\beta \in \mathbb {B}_{\mathfrak {p}}$
.
Proof. Suppose
![]() $\mathrm {Hdg}_{\beta _{0}}(A)<p/(p+1)$
for some
$\mathrm {Hdg}_{\beta _{0}}(A)<p/(p+1)$
for some
![]() $\beta _{0}\in \mathbb {B}_{\mathfrak {p}}$
. Since we have
$\beta _{0}\in \mathbb {B}_{\mathfrak {p}}$
. Since we have
![]() $\mathrm {Hdg}_{\beta }(A)\leq p/(p+1)$
for any
$\mathrm {Hdg}_{\beta }(A)\leq p/(p+1)$
for any
![]() $\beta \in \mathbb {B}_{F}$
, the assumption on
$\beta \in \mathbb {B}_{F}$
, the assumption on
![]() $f_{\mathfrak {p}}$
implies that the inequality
$f_{\mathfrak {p}}$
implies that the inequality
holds for any
![]() $\beta \in \mathbb {B}_{\mathfrak {p}}$
. By [Reference Hattori29, Theorem 4.1], the
$\beta \in \mathbb {B}_{\mathfrak {p}}$
. By [Reference Hattori29, Theorem 4.1], the
![]() $\mathcal {O}_{F_{\mathfrak {p}}}$
-
$\mathcal {O}_{F_{\mathfrak {p}}}$
-
![]() $\mathrm {ADBT}_{1}\ A[p]_{\mathfrak {p}}$
has the canonical subgroup
$\mathrm {ADBT}_{1}\ A[p]_{\mathfrak {p}}$
has the canonical subgroup
![]() $\mathcal {C}_{\mathfrak {p}}$
.
$\mathcal {C}_{\mathfrak {p}}$
.
Suppose
![]() $\mathcal {H}_{\mathfrak {p}}\neq \mathcal {C}_{\mathfrak {p}}$
. For any
$\mathcal {H}_{\mathfrak {p}}\neq \mathcal {C}_{\mathfrak {p}}$
. For any
![]() $\beta \in \mathbb {B}_{\mathfrak {p}}$
, [Reference Hattori29, Corollary 5.3(1)] implies that
$\beta \in \mathbb {B}_{\mathfrak {p}}$
, [Reference Hattori29, Corollary 5.3(1)] implies that
 $$ \begin{align*} \mathrm{Hdg}_{\beta}\left(p^{-1}\mathcal{H}_{\mathfrak{p}}/\mathcal{H}_{\mathfrak{p}}\right)=p^{-1}\mathrm{Hdg}_{\sigma\circ\beta}\left(A[p]_{\mathfrak{p}}\right)=p^{-1}\mathrm{Hdg}_{\sigma\circ\beta}(A[p])\leq 1/(p+1) \end{align*} $$
$$ \begin{align*} \mathrm{Hdg}_{\beta}\left(p^{-1}\mathcal{H}_{\mathfrak{p}}/\mathcal{H}_{\mathfrak{p}}\right)=p^{-1}\mathrm{Hdg}_{\sigma\circ\beta}\left(A[p]_{\mathfrak{p}}\right)=p^{-1}\mathrm{Hdg}_{\sigma\circ\beta}(A[p])\leq 1/(p+1) \end{align*} $$
and that
![]() $A[p]_{\mathfrak {p}}/\mathcal {H}_{\mathfrak {p}}$
is the canonical subgroup of
$A[p]_{\mathfrak {p}}/\mathcal {H}_{\mathfrak {p}}$
is the canonical subgroup of
![]() $p^{-1}\mathcal {H}_{\mathfrak {p}}/\mathcal {H}_{\mathfrak {p}}$
. Thus we have
$p^{-1}\mathcal {H}_{\mathfrak {p}}/\mathcal {H}_{\mathfrak {p}}$
. Thus we have
 $$ \begin{align*} \deg_{\beta}(A[p]/\mathcal{H})=\deg_{\beta}\left(A[p]_{\mathfrak{p}}/\mathcal{H}_{\mathfrak{p}}\right)=1-\mathrm{Hdg}_{\beta}\left(p^{-1}\mathcal{H}_{\mathfrak{p}}/\mathcal{H}_{\mathfrak{p}}\right)\geq p/(p+1), \end{align*} $$
$$ \begin{align*} \deg_{\beta}(A[p]/\mathcal{H})=\deg_{\beta}\left(A[p]_{\mathfrak{p}}/\mathcal{H}_{\mathfrak{p}}\right)=1-\mathrm{Hdg}_{\beta}\left(p^{-1}\mathcal{H}_{\mathfrak{p}}/\mathcal{H}_{\mathfrak{p}}\right)\geq p/(p+1), \end{align*} $$
which yields
![]() $\deg _{\beta }(A[p]/\mathcal {H})=p/(p+1)$
and
$\deg _{\beta }(A[p]/\mathcal {H})=p/(p+1)$
and
![]() $\mathrm {Hdg}_{\beta }(A[p])=p/(p+1)$
for any
$\mathrm {Hdg}_{\beta }(A[p])=p/(p+1)$
for any
![]() $\beta \in \mathbb {B}_{\mathfrak {p}}$
. This contradicts the choice of
$\beta \in \mathbb {B}_{\mathfrak {p}}$
. This contradicts the choice of
![]() $\beta _{0}$
.
$\beta _{0}$
.
Corollary 3.9. Suppose
![]() $f_{\mathfrak {p}}\leq 2$
for any
$f_{\mathfrak {p}}\leq 2$
for any
![]() $\mathfrak {p}\mid p$
. Let
$\mathfrak {p}\mid p$
. Let
![]() $L/K$
be a finite extension. Let
$L/K$
be a finite extension. Let
![]() $[(A^{\prime },\mathcal {H}^{\prime })]$
be an element of
$[(A^{\prime },\mathcal {H}^{\prime })]$
be an element of
![]() $Y_{\mathfrak {c},p}(\mathcal {O}_{L})$
such that
$Y_{\mathfrak {c},p}(\mathcal {O}_{L})$
such that
![]() $\left [\left (A^{\prime }_{L},\mathcal {H}^{\prime }_{L}\right )\right ]\in \mathcal {V}_{\mathfrak {c},Q}(L)$
. Then for any finite flat closed p-cyclic
$\left [\left (A^{\prime }_{L},\mathcal {H}^{\prime }_{L}\right )\right ]\in \mathcal {V}_{\mathfrak {c},Q}(L)$
. Then for any finite flat closed p-cyclic
![]() $\mathcal {O}_{F}$
-subgroup scheme
$\mathcal {O}_{F}$
-subgroup scheme
![]() $\mathcal {D}$
of
$\mathcal {D}$
of
![]() $A^{\prime }[p]$
over
$A^{\prime }[p]$
over
![]() $\mathcal {O}_{L}$
satisfying
$\mathcal {O}_{L}$
satisfying
![]() $\mathcal {D}_{L}\cap \mathcal {H}^{\prime }_{L}=0$
, we have
$\mathcal {D}_{L}\cap \mathcal {H}^{\prime }_{L}=0$
, we have
 $$ \begin{align*} \mathrm{Hdg}_{\beta}(A^{\prime}/\mathcal{D})\leq 1/(p+1) \end{align*} $$
$$ \begin{align*} \mathrm{Hdg}_{\beta}(A^{\prime}/\mathcal{D})\leq 1/(p+1) \end{align*} $$
for any
![]() $\beta \in \mathbb {B}_{F}$
, and
$\beta \in \mathbb {B}_{F}$
, and
![]() $A^{\prime }[p]/\mathcal {D}$
is the canonical subgroup of
$A^{\prime }[p]/\mathcal {D}$
is the canonical subgroup of
![]() $A^{\prime }/\mathcal {D}$
of level
$A^{\prime }/\mathcal {D}$
of level
![]() $1$
.
$1$
.
Proof. Write
 $\mathcal {D}=\bigoplus _{\mathfrak {p}\mid p} \mathcal {D}_{\mathfrak {p}}$
. The assumption implies
$\mathcal {D}=\bigoplus _{\mathfrak {p}\mid p} \mathcal {D}_{\mathfrak {p}}$
. The assumption implies
![]() $\mathcal {D}_{\mathfrak {p}}\neq \mathcal {H}^{\prime }_{\mathfrak {p}}$
for any
$\mathcal {D}_{\mathfrak {p}}\neq \mathcal {H}^{\prime }_{\mathfrak {p}}$
for any
![]() $\mathfrak {p}\mid p$
. If
$\mathfrak {p}\mid p$
. If
![]() $\mathcal {H}^{\prime }_{\mathfrak {p}}$
is the canonical subgroup of
$\mathcal {H}^{\prime }_{\mathfrak {p}}$
is the canonical subgroup of
![]() $A^{\prime }[p]_{\mathfrak {p}}$
, then [Reference Hattori29, Corollary 5.3(1)] implies that
$A^{\prime }[p]_{\mathfrak {p}}$
, then [Reference Hattori29, Corollary 5.3(1)] implies that
 $$ \begin{align*} \mathrm{Hdg}_{\beta}(A^{\prime}/\mathcal{D})=\mathrm{Hdg}_{\beta}\left(p^{-1}\mathcal{D}_{\mathfrak{p}}/\mathcal{D}_{\mathfrak{p}}\right)=p^{-1}\mathrm{Hdg}_{\sigma\circ\beta}(A^{\prime}[p])\leq 1/(p+1) \end{align*} $$
$$ \begin{align*} \mathrm{Hdg}_{\beta}(A^{\prime}/\mathcal{D})=\mathrm{Hdg}_{\beta}\left(p^{-1}\mathcal{D}_{\mathfrak{p}}/\mathcal{D}_{\mathfrak{p}}\right)=p^{-1}\mathrm{Hdg}_{\sigma\circ\beta}(A^{\prime}[p])\leq 1/(p+1) \end{align*} $$
for any
![]() $\beta \in \mathbb {B}_{\mathfrak {p}}$
and that
$\beta \in \mathbb {B}_{\mathfrak {p}}$
and that
![]() $A^{\prime }[p]_{\mathfrak {p}}/\mathcal {D}_{\mathfrak {p}}$
is the canonical subgroup of
$A^{\prime }[p]_{\mathfrak {p}}/\mathcal {D}_{\mathfrak {p}}$
is the canonical subgroup of
![]() $p^{-1}\mathcal {D}_{\mathfrak {p}}/\mathcal {D}_{\mathfrak {p}}=(A^{\prime }/\mathcal {D})[p]_{\mathfrak {p}}$
. Otherwise, Lemma 3.8 yields
$p^{-1}\mathcal {D}_{\mathfrak {p}}/\mathcal {D}_{\mathfrak {p}}=(A^{\prime }/\mathcal {D})[p]_{\mathfrak {p}}$
. Otherwise, Lemma 3.8 yields
![]() $\mathrm {Hdg}_{\beta }(A^{\prime })=p/(p+1)$
for any
$\mathrm {Hdg}_{\beta }(A^{\prime })=p/(p+1)$
for any
![]() $\beta \in \mathbb {B}_{\mathfrak {p}}$
. By [Reference Hattori29, Proposition 6.1], we see that
$\beta \in \mathbb {B}_{\mathfrak {p}}$
. By [Reference Hattori29, Proposition 6.1], we see that
 $$ \begin{align*} \deg_{\beta}\left(A^{\prime}[p]_{\mathfrak{p}}/\mathcal{D}_{\mathfrak{p}}\right)=p/(p+1),\qquad \mathrm{Hdg}_{\beta}\left((A^{\prime}/\mathcal{D})[p]_{\mathfrak{p}}\right)=1/(p+1) \end{align*} $$
$$ \begin{align*} \deg_{\beta}\left(A^{\prime}[p]_{\mathfrak{p}}/\mathcal{D}_{\mathfrak{p}}\right)=p/(p+1),\qquad \mathrm{Hdg}_{\beta}\left((A^{\prime}/\mathcal{D})[p]_{\mathfrak{p}}\right)=1/(p+1) \end{align*} $$
for any
![]() $\beta \in \mathbb {B}_{\mathfrak {p}}$
and that
$\beta \in \mathbb {B}_{\mathfrak {p}}$
and that
![]() $(A^{\prime }/\mathcal {D})[p]_{\mathfrak {p}}$
has the canonical subgroup
$(A^{\prime }/\mathcal {D})[p]_{\mathfrak {p}}$
has the canonical subgroup
![]() $A^{\prime }[p]_{\mathfrak {p}}/\mathcal {D}_{\mathfrak {p}}$
. Hence the HBAV
$A^{\prime }[p]_{\mathfrak {p}}/\mathcal {D}_{\mathfrak {p}}$
. Hence the HBAV
![]() $A^{\prime }/\mathcal {D}$
satisfies
$A^{\prime }/\mathcal {D}$
satisfies
 $$ \begin{align*} \mathrm{Hdg}_{\beta}(A^{\prime}/\mathcal{D})\leq 1/(p+1) \end{align*} $$
$$ \begin{align*} \mathrm{Hdg}_{\beta}(A^{\prime}/\mathcal{D})\leq 1/(p+1) \end{align*} $$
for any
![]() $\beta \in \mathbb {B}_{F}$
and has the canonical subgroup
$\beta \in \mathbb {B}_{F}$
and has the canonical subgroup
 $$ \begin{align*} A^{\prime}[p]/\mathcal{D}=\bigoplus_{\mathfrak{p}\mid p} A^{\prime}[p]_{\mathfrak{p}}/\mathcal{D}_{\mathfrak{p}} \end{align*} $$
$$ \begin{align*} A^{\prime}[p]/\mathcal{D}=\bigoplus_{\mathfrak{p}\mid p} A^{\prime}[p]_{\mathfrak{p}}/\mathcal{D}_{\mathfrak{p}} \end{align*} $$
of level
![]() $1$
. This concludes the proof of the corollary.
$1$
. This concludes the proof of the corollary.
Lemma 3.10. Suppose
![]() $f_{\mathfrak {p}}\leq 2$
for any
$f_{\mathfrak {p}}\leq 2$
for any
![]() $\mathfrak {p}\mid p$
. Then we have
$\mathfrak {p}\mid p$
. Then we have
 $$ \begin{align*} \mathcal{V}_{\mathfrak{c},Q}\left(\tfrac{1}{p+1}\right)\neq \emptyset. \end{align*} $$
$$ \begin{align*} \mathcal{V}_{\mathfrak{c},Q}\left(\tfrac{1}{p+1}\right)\neq \emptyset. \end{align*} $$
Moreover, for any finite extension
![]() $L/K$
and any element
$L/K$
and any element
![]() $[(A^{\prime },\mathcal {H}^{\prime })]$
of
$[(A^{\prime },\mathcal {H}^{\prime })]$
of
![]() $Y_{\mathfrak {c},p}(\mathcal {O}_{L})$
satisfying
$Y_{\mathfrak {c},p}(\mathcal {O}_{L})$
satisfying
 $\left [\left (A^{\prime }_{L},\mathcal {H}^{\prime }_{L}\right )\right ]\in \mathcal {V}_{\mathfrak {c},Q}\left (\tfrac {1}{p+1}\right )(L)$
, we have
$\left [\left (A^{\prime }_{L},\mathcal {H}^{\prime }_{L}\right )\right ]\in \mathcal {V}_{\mathfrak {c},Q}\left (\tfrac {1}{p+1}\right )(L)$
, we have
![]() $\mathrm {Hdg}_{\beta }(A^{\prime })\leq 1/(p+1)$
for any
$\mathrm {Hdg}_{\beta }(A^{\prime })\leq 1/(p+1)$
for any
![]() $\beta \in \mathbb {B}_{F}$
and the HBAV
$\beta \in \mathbb {B}_{F}$
and the HBAV
![]() $A^{\prime }$
has the canonical subgroup
$A^{\prime }$
has the canonical subgroup
![]() $\mathcal {H}^{\prime }$
.
$\mathcal {H}^{\prime }$
.
Proof. Recall that we have
 $\mathrm {sp}^{-1}\left (\bar {Q}\right )=(\mathrm {Spf}(\mathfrak {B}^{\prime }))^{\mathrm {rig}}$
with the ring
$\mathrm {sp}^{-1}\left (\bar {Q}\right )=(\mathrm {Spf}(\mathfrak {B}^{\prime }))^{\mathrm {rig}}$
with the ring
![]() $\mathfrak {B}^{\prime }$
of equation (3.4) in the proof of Proposition 3.7. From the description of
$\mathfrak {B}^{\prime }$
of equation (3.4) in the proof of Proposition 3.7. From the description of
![]() $\deg _{\beta }$
in terms of the parameter
$\deg _{\beta }$
in terms of the parameter
![]() $X_{\beta }$
of the ring
$X_{\beta }$
of the ring
![]() $\mathfrak {B}^{\prime }$
, we see that there exists a point
$\mathfrak {B}^{\prime }$
, we see that there exists a point
![]() $[(A^{\prime },\mathcal {H}^{\prime })]\in Y_{\mathfrak {c},p}(\mathcal {O}_{L})$
with some finite extension
$[(A^{\prime },\mathcal {H}^{\prime })]\in Y_{\mathfrak {c},p}(\mathcal {O}_{L})$
with some finite extension
![]() $L/K$
such that
$L/K$
such that
 $\left [\left (A^{\prime }_{L},\mathcal {H}^{\prime }_{L}\right )\right ]\in \mathrm {sp}^{-1}\left (\bar {Q}\right )$
and
$\left [\left (A^{\prime }_{L},\mathcal {H}^{\prime }_{L}\right )\right ]\in \mathrm {sp}^{-1}\left (\bar {Q}\right )$
and
 $$ \begin{align*} \deg_{\beta}(A^{\prime}[p]/\mathcal{H}^{\prime})=1/(p+1) \end{align*} $$
$$ \begin{align*} \deg_{\beta}(A^{\prime}[p]/\mathcal{H}^{\prime})=1/(p+1) \end{align*} $$
for any
![]() $\beta \in \mathbb {B}_{F}$
. Then [Reference Hattori29, Lemma 5.1(1)] implies that
$\beta \in \mathbb {B}_{F}$
. Then [Reference Hattori29, Lemma 5.1(1)] implies that
![]() $\mathrm {Hdg}_{\beta }(A^{\prime })=1/(p+1)$
for any
$\mathrm {Hdg}_{\beta }(A^{\prime })=1/(p+1)$
for any
![]() $\beta \in \mathbb {B}_{F}$
and thus
$\beta \in \mathbb {B}_{F}$
and thus
 $\left [\left (A^{\prime }_{L},\mathcal {H}^{\prime }_{L}\right )\right ]\in \mathcal {V}_{\mathfrak {c},Q}\left (\tfrac {1}{p+1}\right )(L)$
. The last assertion also follows from [Reference Hattori29, Lemma 5.1(1)].
$\left [\left (A^{\prime }_{L},\mathcal {H}^{\prime }_{L}\right )\right ]\in \mathcal {V}_{\mathfrak {c},Q}\left (\tfrac {1}{p+1}\right )(L)$
. The last assertion also follows from [Reference Hattori29, Lemma 5.1(1)].
Since
![]() $\mathcal {Y}_{\mathfrak {c},p}$
is separated, Proposition 3.7 implies that the base extension
$\mathcal {Y}_{\mathfrak {c},p}$
is separated, Proposition 3.7 implies that the base extension
 $\mathcal {V}_{\mathfrak {c},Q,\mathbb {C}_{p}}=\mathcal {V}_{\mathfrak {c},Q}\hat {\otimes }_{K} \mathbb {C}_{p}$
is an admissible affinoid open subset of
$\mathcal {V}_{\mathfrak {c},Q,\mathbb {C}_{p}}=\mathcal {V}_{\mathfrak {c},Q}\hat {\otimes }_{K} \mathbb {C}_{p}$
is an admissible affinoid open subset of
![]() $\mathcal {Y}_{\mathfrak {c},p,\mathbb {C}_{p}}$
whose connected components are all isomorphic to
$\mathcal {Y}_{\mathfrak {c},p,\mathbb {C}_{p}}$
whose connected components are all isomorphic to
![]() $\mathcal {V}_{\mathfrak {c},Q}\hat {\otimes }_{K^{\prime }} \mathbb {C}_{p}$
. Each connected component contains an affinoid subdomain of
$\mathcal {V}_{\mathfrak {c},Q}\hat {\otimes }_{K^{\prime }} \mathbb {C}_{p}$
. Each connected component contains an affinoid subdomain of
 $\mathcal {V}_{\mathfrak {c},Q}\left (\tfrac {1}{p+1}\right )\hat {\otimes }_{K} \mathbb {C}_{p}$
which is isomorphic to
$\mathcal {V}_{\mathfrak {c},Q}\left (\tfrac {1}{p+1}\right )\hat {\otimes }_{K} \mathbb {C}_{p}$
which is isomorphic to
 $\mathcal {V}_{\mathfrak {c},Q}\left (\tfrac {1}{p+1}\right ) \hat {\otimes }_{K^{\prime }} \mathbb {C}_{p}$
. By Lemma 3.10, we have
$\mathcal {V}_{\mathfrak {c},Q}\left (\tfrac {1}{p+1}\right ) \hat {\otimes }_{K^{\prime }} \mathbb {C}_{p}$
. By Lemma 3.10, we have
 $$ \begin{align*} \mathcal{V}_{\mathfrak{c},Q}\left(\tfrac{1}{p+1}\right)\hat{\otimes}_{K^{\prime}} \mathbb{C}_{p}\neq \emptyset. \end{align*} $$
$$ \begin{align*} \mathcal{V}_{\mathfrak{c},Q}\left(\tfrac{1}{p+1}\right)\hat{\otimes}_{K^{\prime}} \mathbb{C}_{p}\neq \emptyset. \end{align*} $$
The point
![]() $Q\in \mathcal {Y}_{\mathfrak {c},p}(L)$
defines a point of
$Q\in \mathcal {Y}_{\mathfrak {c},p}(L)$
defines a point of
![]() $\mathcal {Y}_{\mathfrak {c},p,\mathbb {C}_{p}}\left (\mathbb {C}_{p}\right )$
by the natural inclusion
$\mathcal {Y}_{\mathfrak {c},p,\mathbb {C}_{p}}\left (\mathbb {C}_{p}\right )$
by the natural inclusion
![]() $L\to \mathbb {C}_{p}$
, which we also denote by Q. Let
$L\to \mathbb {C}_{p}$
, which we also denote by Q. Let
 $ \mathcal {V}^{0}_{\mathfrak {c},Q,\mathbb {C}_{p}}$
be the connected component of
$ \mathcal {V}^{0}_{\mathfrak {c},Q,\mathbb {C}_{p}}$
be the connected component of
![]() $\mathcal {V}_{\mathfrak {c},Q,\mathbb {C}_{p}}$
containing Q and let
$\mathcal {V}_{\mathfrak {c},Q,\mathbb {C}_{p}}$
containing Q and let
 $\mathcal {V}^{0}_{\mathfrak {c},Q,\mathbb {C}_{p}}\left (\tfrac {1}{p+1}\right )$
be a copy of
$\mathcal {V}^{0}_{\mathfrak {c},Q,\mathbb {C}_{p}}\left (\tfrac {1}{p+1}\right )$
be a copy of
 $\mathcal {V}_{\mathfrak {c},Q}\left (\tfrac {1}{p+1}\right ) \hat {\otimes }_{K^{\prime }} \mathbb {C}_{p}$
which is contained in
$\mathcal {V}_{\mathfrak {c},Q}\left (\tfrac {1}{p+1}\right ) \hat {\otimes }_{K^{\prime }} \mathbb {C}_{p}$
which is contained in
 $\mathcal {V}^{0}_{\mathfrak {c},Q,\mathbb {C}_{p}}$
. These are both nonempty admissible affinoid open subsets of
$\mathcal {V}^{0}_{\mathfrak {c},Q,\mathbb {C}_{p}}$
. These are both nonempty admissible affinoid open subsets of
![]() $\mathcal {Y}_{\mathfrak {c},p,\mathbb {C}_{p}}$
.
$\mathcal {Y}_{\mathfrak {c},p,\mathbb {C}_{p}}$
.
3.3 Overconvergent Hilbert modular forms and the eigenvariety
In this subsection, we recall the construction of sheaves of overconvergent Hilbert modular forms and the associated eigenvariety, due to Andreatta, Iovita, and Pilloni [Reference Andreatta, Iovita and Pilloni4].
3.3.1 Overconvergent modular forms over Hilbert modular varieties
Put
![]() $\mathbb {T}=\mathrm {Res}_{\mathcal {O}_{F}/\mathbb {Z}}(\mathbb {G}_{\mathrm {m}})$
. Let
$\mathbb {T}=\mathrm {Res}_{\mathcal {O}_{F}/\mathbb {Z}}(\mathbb {G}_{\mathrm {m}})$
. Let
![]() $\hat {\mathbb {T}}$
be its formal completion along the unit section. For any
$\hat {\mathbb {T}}$
be its formal completion along the unit section. For any
![]() $w \in e^{-1}\mathbb {Z}_{\geq 1}$
, let
$w \in e^{-1}\mathbb {Z}_{\geq 1}$
, let
![]() $\mathbb {T}_{w}^{0}$
be the formal subgroup scheme of
$\mathbb {T}_{w}^{0}$
be the formal subgroup scheme of
![]() $\hat {\mathbb {T}}$
over
$\hat {\mathbb {T}}$
over
![]() $\mathrm {Spf}(\mathcal {O}_{K})$
representing the functor
$\mathrm {Spf}(\mathcal {O}_{K})$
representing the functor
on the category of admissible formal
![]() $\mathcal {O}_{K}$
-algebras
$\mathcal {O}_{K}$
-algebras
![]() $\mathfrak {B}$
. Then
$\mathfrak {B}$
. Then
![]() $\mathbb {T}^{0}_{w}$
is a quasi-compact admissible formal group scheme over
$\mathbb {T}^{0}_{w}$
is a quasi-compact admissible formal group scheme over
![]() $\mathcal {O}_{K}$
.
$\mathcal {O}_{K}$
.
Let
![]() $\mathcal {W}$
be the Berthelot generic fiber of
$\mathcal {W}$
be the Berthelot generic fiber of
![]() $\mathrm {Spf}\left (\mathcal {O}_{K}\left [\left [\mathbb {T}\left (\mathbb {Z}_{p}\right )\right ]\right ]\right )$
and denote the universal character on this space by
$\mathrm {Spf}\left (\mathcal {O}_{K}\left [\left [\mathbb {T}\left (\mathbb {Z}_{p}\right )\right ]\right ]\right )$
and denote the universal character on this space by
Here
![]() $\mathcal {O}^{\circ }$
is the sheaf of rigid analytic functions with absolute value bounded by
$\mathcal {O}^{\circ }$
is the sheaf of rigid analytic functions with absolute value bounded by
![]() $1$
and the last equality follows from [Reference de Jong19, Theorem 7.4.1]. For any morphism
$1$
and the last equality follows from [Reference de Jong19, Theorem 7.4.1]. For any morphism
![]() $\mathcal {X}\to \mathcal {W}$
of rigid analytic varieties over K, we denote by
$\mathcal {X}\to \mathcal {W}$
of rigid analytic varieties over K, we denote by
![]() $\kappa ^{\mathcal {X}}$
the restriction
$\kappa ^{\mathcal {X}}$
the restriction
 $$ \begin{align*} \kappa^{\mathcal{X}}:\mathbb{T}\left(\mathbb{Z}_{p}\right)\overset{\kappa^{\mathrm{un}}}{\to}\mathcal{O}^{\circ}(\mathcal{W})^{\times} \to \mathcal{O}^{\circ}(\mathcal{X})^{\times} \end{align*} $$
$$ \begin{align*} \kappa^{\mathcal{X}}:\mathbb{T}\left(\mathbb{Z}_{p}\right)\overset{\kappa^{\mathrm{un}}}{\to}\mathcal{O}^{\circ}(\mathcal{W})^{\times} \to \mathcal{O}^{\circ}(\mathcal{X})^{\times} \end{align*} $$
of
![]() $\kappa ^{\mathrm {un}}$
to
$\kappa ^{\mathrm {un}}$
to
![]() $\mathcal {X}$
. Consider the case where
$\mathcal {X}$
. Consider the case where
![]() $\mathcal {X}$
is a reduced K-affinoid variety
$\mathcal {X}$
is a reduced K-affinoid variety
![]() $\mathcal {U}=\mathrm {Sp}(A)$
. Then the subring
$\mathcal {U}=\mathrm {Sp}(A)$
. Then the subring
![]() $A^{\circ }$
of power-bounded elements is p-adically complete. For any positive integer n, put
$A^{\circ }$
of power-bounded elements is p-adically complete. For any positive integer n, put
![]() $q_{n}=2$
if
$q_{n}=2$
if
![]() $p=2$
and
$p=2$
and
![]() $n=1$
, and
$n=1$
, and
![]() $q_{n}=1$
otherwise. When we consider the case of
$q_{n}=1$
otherwise. When we consider the case of
![]() $p=2$
and
$p=2$
and
![]() $n=1$
, we assume that
$n=1$
, we assume that
![]() $2$
splits completely in F. The character
$2$
splits completely in F. The character
![]() $\kappa ^{\mathcal {U}}$
is said to be n-analytic if the restriction to
$\kappa ^{\mathcal {U}}$
is said to be n-analytic if the restriction to
![]() $\mathbb {T}^{0}_{n}\left (\mathbb {Z}_{p}\right )$
factors as
$\mathbb {T}^{0}_{n}\left (\mathbb {Z}_{p}\right )$
factors as

with some
![]() $\mathbb {Z}_{p}$
-linear map
$\mathbb {Z}_{p}$
-linear map
![]() $\psi $
. In this case, we also say that the morphism
$\psi $
. In this case, we also say that the morphism
![]() $\mathcal {U}\to \mathcal {W}$
is n-analytic. Any
$\mathcal {U}\to \mathcal {W}$
is n-analytic. Any
![]() $\kappa ^{\mathcal {U}}$
is n-analytic for some n by the maximal modulus principle. Note that any n-analytic character defines an analytic character
$\kappa ^{\mathcal {U}}$
is n-analytic for some n by the maximal modulus principle. Note that any n-analytic character defines an analytic character
![]() $\mathbb {T}^{0}_{n}\left (\mathbb {Z}_{p}\right )\to A^{\times }$
, even for the case of
$\mathbb {T}^{0}_{n}\left (\mathbb {Z}_{p}\right )\to A^{\times }$
, even for the case of
![]() $p=2$
and
$p=2$
and
![]() $n=1$
. Moreover, put
$n=1$
. Moreover, put
 $$ \begin{align*} \delta_{n}= \begin{cases} \frac{1}{p-1}& (p\geq 3)\\ \frac{1}{4}& (p=2,\ n=1)\\ 0& (p=2,\ n\geq 2). \end{cases} \end{align*} $$
$$ \begin{align*} \delta_{n}= \begin{cases} \frac{1}{p-1}& (p\geq 3)\\ \frac{1}{4}& (p=2,\ n=1)\\ 0& (p=2,\ n\geq 2). \end{cases} \end{align*} $$
Then for any
![]() $w\in e^{-1}\mathbb {Z}$
satisfying
$w\in e^{-1}\mathbb {Z}$
satisfying
any n-analytic character extends to an analytic character
![]() $\mathbb {T}^{0}_{w}(\mathcal {O}_{K})\to A^{\times }$
.
$\mathbb {T}^{0}_{w}(\mathcal {O}_{K})\to A^{\times }$
.
Using [Reference Hattori29, Theorem 8.1] and Lemma 3.5, we can generalize the construction in [Reference Andreatta, Iovita and Pilloni4, §3.3]. Let n be a positive integer and put
 $$ \begin{align} B_{n}= \begin{cases} \frac{p-2}{p^{n}}& (p\geq 3)\\ \frac{3}{8}& (p=2,\ n=1)\\ \frac{p-1}{p^{n}}& (p=2,\ n\geq 2), \end{cases} \end{align} $$
$$ \begin{align} B_{n}= \begin{cases} \frac{p-2}{p^{n}}& (p\geq 3)\\ \frac{3}{8}& (p=2,\ n=1)\\ \frac{p-1}{p^{n}}& (p=2,\ n\geq 2), \end{cases} \end{align} $$
so that we have
 $$ \begin{align*} \frac{1}{p+1}<B_{1}. \end{align*} $$
$$ \begin{align*} \frac{1}{p+1}<B_{1}. \end{align*} $$
Let
 $\underline {v}=\left (v_{\beta }\right )_{\beta \in \mathbb {B}_{F}}$
be a g-tuple in
$\underline {v}=\left (v_{\beta }\right )_{\beta \in \mathbb {B}_{F}}$
be a g-tuple in
![]() $[0,B_{n})\cap \mathbb {Q}$
. Put
$[0,B_{n})\cap \mathbb {Q}$
. Put
![]() $v=\max \left \{v_{\beta }\mid \beta \in \mathbb {B}_{F}\right \}$
. Let
$v=\max \left \{v_{\beta }\mid \beta \in \mathbb {B}_{F}\right \}$
. Let
![]() $C_{n}$
be the canonical subgroup of
$C_{n}$
be the canonical subgroup of
![]() $\bar {\mathcal {A}}^{\mathrm {un}}$
of level n over
$\bar {\mathcal {A}}^{\mathrm {un}}$
of level n over
![]() $\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
, as before. Put
$\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
, as before. Put
 $$ \begin{align*} \bar{\mathcal{M}}(\Gamma_{1}(p^{n}),\mu_{N},\mathfrak{c})\left(\underline{v}\right)=\mathrm{Isom}_{\bar{\mathcal{M}}\left(\mu_{N},\mathfrak{c}\right)\left(\underline{v}\right)}\left(C_{n}, \mathcal{D}_{F}^{-1}\otimes \mu_{p^{n}}\right). \end{align*} $$
$$ \begin{align*} \bar{\mathcal{M}}(\Gamma_{1}(p^{n}),\mu_{N},\mathfrak{c})\left(\underline{v}\right)=\mathrm{Isom}_{\bar{\mathcal{M}}\left(\mu_{N},\mathfrak{c}\right)\left(\underline{v}\right)}\left(C_{n}, \mathcal{D}_{F}^{-1}\otimes \mu_{p^{n}}\right). \end{align*} $$
We denote by
![]() $\bar {\mathfrak {M}}(\Gamma _{1}(p^{n}),\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
the normalization of
$\bar {\mathfrak {M}}(\Gamma _{1}(p^{n}),\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
the normalization of
![]() $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
in
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
in
![]() $\bar {\mathcal {M}}(\Gamma _{1}(p^{n}), \mu _{N}, \mathfrak {c})\left (\underline {v}\right )$
. Note that since
$\bar {\mathcal {M}}(\Gamma _{1}(p^{n}), \mu _{N}, \mathfrak {c})\left (\underline {v}\right )$
. Note that since
![]() $\mathcal {C}^{\vee }_{n}$
is finite and étale over
$\mathcal {C}^{\vee }_{n}$
is finite and étale over
![]() $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)$
, we have
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)$
, we have
 $$ \begin{align} \bar{\mathfrak{M}}(\Gamma_{1}(p^{n}),\mu_{N},\mathfrak{c})(0)=\mathrm{Isom}_{\bar{\mathfrak{M}}\left(\mu_{N},\mathfrak{c}\right)(0)}\left(\mathcal{C}_{n}, \mathcal{D}_{F}^{-1}\otimes \mu_{p^{n}}\right), \end{align} $$
$$ \begin{align} \bar{\mathfrak{M}}(\Gamma_{1}(p^{n}),\mu_{N},\mathfrak{c})(0)=\mathrm{Isom}_{\bar{\mathfrak{M}}\left(\mu_{N},\mathfrak{c}\right)(0)}\left(\mathcal{C}_{n}, \mathcal{D}_{F}^{-1}\otimes \mu_{p^{n}}\right), \end{align} $$
which is a
![]() $\mathbb {T}(\mathbb {Z}/p^{n}\mathbb {Z})$
-torsor over
$\mathbb {T}(\mathbb {Z}/p^{n}\mathbb {Z})$
-torsor over
![]() $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)$
.
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)$
.
Let w be an element of
![]() $e^{-1}\mathbb {Z}$
satisfying
$e^{-1}\mathbb {Z}$
satisfying
 $$ \begin{align*} n-1+\delta_{n}< w\leq n-\frac{v(p^{n}-1)}{p-1}-\delta_{K}(v), \end{align*} $$
$$ \begin{align*} n-1+\delta_{n}< w\leq n-\frac{v(p^{n}-1)}{p-1}-\delta_{K}(v), \end{align*} $$
which exists if
 $$ \begin{align} 1-\delta_{n}-\frac{p^{n} v}{p-1}\geq \frac{2}{e}. \end{align} $$
$$ \begin{align} 1-\delta_{n}-\frac{p^{n} v}{p-1}\geq \frac{2}{e}. \end{align} $$
Note that condition (3.7) is satisfied for a sufficiently large K. Let
![]() $\mathcal {F}$
be the locally free
$\mathcal {F}$
be the locally free
![]() $\mathcal {O}_{F}\otimes \mathcal {O}_{\bar {\mathfrak {M}}\left (\Gamma _{1}\left (p^{n}\right ),\mu _{N},\mathfrak {c}\right )\left (\underline {v}\right )}$
-module of rank
$\mathcal {O}_{F}\otimes \mathcal {O}_{\bar {\mathfrak {M}}\left (\Gamma _{1}\left (p^{n}\right ),\mu _{N},\mathfrak {c}\right )\left (\underline {v}\right )}$
-module of rank
![]() $1$
constructed as in [Reference Andreatta, Iovita and Pilloni4, Proposition 3.4], using Lemma 3.5 for
$1$
constructed as in [Reference Andreatta, Iovita and Pilloni4, Proposition 3.4], using Lemma 3.5 for
![]() $i=w+\delta _{K}(v)$
. Let
$i=w+\delta _{K}(v)$
. Let
be the p-adic formal
![]() $\mathbb {T}^{0}_{w}$
-torsor over
$\mathbb {T}^{0}_{w}$
-torsor over
![]() $\bar {\mathfrak {M}}(\Gamma _{1}(p^{n}),\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
classifying, for any
$\bar {\mathfrak {M}}(\Gamma _{1}(p^{n}),\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
classifying, for any
![]() $R\in \mathbf {NAdm}$
and any morphism of p-adic formal schemes
$R\in \mathbf {NAdm}$
and any morphism of p-adic formal schemes
![]() $\gamma :\mathrm {Spf}(R)\to \bar {\mathfrak {M}}(\Gamma _{1}(p^{n}),\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
, the isomorphisms
$\gamma :\mathrm {Spf}(R)\to \bar {\mathfrak {M}}(\Gamma _{1}(p^{n}),\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
, the isomorphisms
![]() $\alpha : \gamma ^{*}\mathcal {F}\to \mathcal {O}_{F}\otimes R$
such that the composite
$\alpha : \gamma ^{*}\mathcal {F}\to \mathcal {O}_{F}\otimes R$
such that the composite
 $$ \begin{align*} \underline{\mathcal{O}_{F}/p^{n} \mathcal{O}_{F}}(R) \overset{\gamma}{\simeq} \mathcal{C}_{n}^{\vee}(R)\overset{\mathrm{HT}_{w}}{\to} \gamma^{*}\mathcal{F}/\pi_{K}^{ew} \gamma^{*}\mathcal{F} \overset{\alpha}{\simeq} \mathcal{O}_{F}\otimes R/\pi_{K}^{e w} R \end{align*} $$
$$ \begin{align*} \underline{\mathcal{O}_{F}/p^{n} \mathcal{O}_{F}}(R) \overset{\gamma}{\simeq} \mathcal{C}_{n}^{\vee}(R)\overset{\mathrm{HT}_{w}}{\to} \gamma^{*}\mathcal{F}/\pi_{K}^{ew} \gamma^{*}\mathcal{F} \overset{\alpha}{\simeq} \mathcal{O}_{F}\otimes R/\pi_{K}^{e w} R \end{align*} $$
sends
![]() $1$
to
$1$
to
![]() $1$
[Reference Andreatta, Iovita and Pilloni4, §3.4]. We also write
$1$
[Reference Andreatta, Iovita and Pilloni4, §3.4]. We also write
![]() $\mathfrak {IW}_{w}^{+}$
as
$\mathfrak {IW}_{w}^{+}$
as
 $\mathfrak {IW}^{+}_{w,\mathfrak {c}}\left (\underline {v}\right )$
. We denote the Raynaud generic fiber of
$\mathfrak {IW}^{+}_{w,\mathfrak {c}}\left (\underline {v}\right )$
. We denote the Raynaud generic fiber of
![]() $\mathfrak {IW}_{w}^{+}$
by
$\mathfrak {IW}_{w}^{+}$
by
![]() $\mathcal {IW}_{w}^{+}$
and also by
$\mathcal {IW}_{w}^{+}$
and also by
 $\mathcal {IW}^{+}_{w,\mathfrak {c}}\left (\underline {v}\right )$
. From equality (3.6), we see that the moduli interpretation of
$\mathcal {IW}^{+}_{w,\mathfrak {c}}\left (\underline {v}\right )$
. From equality (3.6), we see that the moduli interpretation of
 $\mathfrak {IW}_{w,\mathfrak {c}}^{+}(0)$
already given is also valid for the category of quasi-idyllic p-adic
$\mathfrak {IW}_{w,\mathfrak {c}}^{+}(0)$
already given is also valid for the category of quasi-idyllic p-adic
![]() $ \mathcal {O}_{K}$
-algebras R.
$ \mathcal {O}_{K}$
-algebras R.
For the structure morphism
we put
![]() $\pi _{w}=h_{n}\circ \gamma _{w}$
. We denote by
$\pi _{w}=h_{n}\circ \gamma _{w}$
. We denote by
![]() $\gamma _{w}^{\mathrm {rig}}$
,
$\gamma _{w}^{\mathrm {rig}}$
,
![]() $h_{n}^{\mathrm {rig}}$
, and
$h_{n}^{\mathrm {rig}}$
, and
![]() $\pi _{w}^{\mathrm {rig}}$
the induced morphisms on the Raynaud generic fibers. Let
$\pi _{w}^{\mathrm {rig}}$
the induced morphisms on the Raynaud generic fibers. Let
![]() $\mathbb {T}_{w}$
be the formal subgroup scheme of
$\mathbb {T}_{w}$
be the formal subgroup scheme of
![]() $\hat {\mathbb {T}}$
over
$\hat {\mathbb {T}}$
over
![]() $\mathrm {Spf}(\mathcal {O}_{K})$
whose set of
$\mathrm {Spf}(\mathcal {O}_{K})$
whose set of
![]() $\mathfrak {B}$
-valued points are the inverse image of
$\mathfrak {B}$
-valued points are the inverse image of
![]() $\mathbb {T}(\mathbb {Z}/p^{n}\mathbb {Z})$
by the map
$\mathbb {T}(\mathbb {Z}/p^{n}\mathbb {Z})$
by the map
![]() $\mathbb {T}(\mathfrak {B})\to \mathbb {T}\left (\mathfrak {B}/\pi _{K}^{e w}\mathfrak {B}\right )$
for any admissible formal
$\mathbb {T}(\mathfrak {B})\to \mathbb {T}\left (\mathfrak {B}/\pi _{K}^{e w}\mathfrak {B}\right )$
for any admissible formal
![]() $\mathcal {O}_{K}$
-algebra
$\mathcal {O}_{K}$
-algebra
![]() $\mathfrak {B}$
. The natural action of
$\mathfrak {B}$
. The natural action of
![]() $\mathbb {T}_{w}^{0}$
on
$\mathbb {T}_{w}^{0}$
on
![]() $\mathfrak {IW}_{w}^{+}$
induces an action of
$\mathfrak {IW}_{w}^{+}$
induces an action of
![]() $\mathbb {T}_{w}$
on
$\mathbb {T}_{w}$
on
![]() $\mathfrak {IW}_{w}^{+}$
over
$\mathfrak {IW}_{w}^{+}$
over
![]() $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
and also on the Raynaud generic fiber
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
and also on the Raynaud generic fiber
![]() $\mathcal {IW}_{w}^{+}$
over
$\mathcal {IW}_{w}^{+}$
over
![]() $\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
. Then for any reduced K-affinoid variety
$\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
. Then for any reduced K-affinoid variety
![]() $\mathcal {U}$
and n-analytic morphism
$\mathcal {U}$
and n-analytic morphism
![]() $\mathcal {U}\to \mathcal {W}$
, we define
$\mathcal {U}\to \mathcal {W}$
, we define
 $$ \begin{align*} \Omega^{\kappa^{\mathcal{U}}}=\left(\pi_{w}^{\mathrm{rig}}\right)_{*}\left(\mathcal{O}_{\mathcal{IW}_{w}^{+}\times \mathcal{U}}\right)\left[-\kappa^{\mathcal{U}}\right]. \end{align*} $$
$$ \begin{align*} \Omega^{\kappa^{\mathcal{U}}}=\left(\pi_{w}^{\mathrm{rig}}\right)_{*}\left(\mathcal{O}_{\mathcal{IW}_{w}^{+}\times \mathcal{U}}\right)\left[-\kappa^{\mathcal{U}}\right]. \end{align*} $$
By [Reference Andreatta, Iovita and Pilloni4, Proposition 3.13], it is an invertible sheaf which is independent of the choices of n and w. Let D be the boundary divisor of
![]() $\bar {\mathcal {M}} (\mu _{N},\mathfrak {c})$
. We also put
$\bar {\mathcal {M}} (\mu _{N},\mathfrak {c})$
. We also put
 $$ \begin{align*} M\left(\mu_{N}, \mathfrak{c}, \kappa^{\mathcal{U}}\right)\left(\underline{v}\right)&=H^{0}\left(\bar{\mathcal{M}}(\mu_{N},\mathfrak{c})\left(\underline{v}\right)\times \mathcal{U}, \Omega^{\kappa^{\mathcal{U}}}\right),\\ S\left(\mu_{N},\mathfrak{c}, \kappa^{\mathcal{U}}\right)\left(\underline{v}\right)&=H^{0}\left(\bar{\mathcal{M}}(\mu_{N},\mathfrak{c})\left(\underline{v}\right)\times \mathcal{U}, \Omega^{\kappa^{\mathcal{U}}}(-D)\right). \end{align*} $$
$$ \begin{align*} M\left(\mu_{N}, \mathfrak{c}, \kappa^{\mathcal{U}}\right)\left(\underline{v}\right)&=H^{0}\left(\bar{\mathcal{M}}(\mu_{N},\mathfrak{c})\left(\underline{v}\right)\times \mathcal{U}, \Omega^{\kappa^{\mathcal{U}}}\right),\\ S\left(\mu_{N},\mathfrak{c}, \kappa^{\mathcal{U}}\right)\left(\underline{v}\right)&=H^{0}\left(\bar{\mathcal{M}}(\mu_{N},\mathfrak{c})\left(\underline{v}\right)\times \mathcal{U}, \Omega^{\kappa^{\mathcal{U}}}(-D)\right). \end{align*} $$
For any
![]() $R\in \mathbf {NAdm}$
, let us consider tuples
$R\in \mathbf {NAdm}$
, let us consider tuples
![]() $(A, \iota ,\lambda ,\psi ,u,\alpha )$
over R consisting of an HBAV
$(A, \iota ,\lambda ,\psi ,u,\alpha )$
over R consisting of an HBAV
![]() $(A,\iota , \lambda ,\psi )$
over
$(A,\iota , \lambda ,\psi )$
over
![]() $\mathrm {Spec}(R)$
such that
$\mathrm {Spec}(R)$
such that
![]() $\mathrm {Hdg}_{\beta }(A_{x})\leq v_{\beta }$
for any
$\mathrm {Hdg}_{\beta }(A_{x})\leq v_{\beta }$
for any
![]() $x\in \mathrm {Sp}(R[1/p])$
, an isomorphism of
$x\in \mathrm {Sp}(R[1/p])$
, an isomorphism of
![]() $\mathcal {O}_{F}$
-group schemes
$\mathcal {O}_{F}$
-group schemes
 $$ \begin{align*} u: \mathcal{C}_{n}\rvert_{R\left[1/p\right]}\simeq \mathcal{D}_{F}^{-1}\otimes\mu_{p^{n}} \end{align*} $$
$$ \begin{align*} u: \mathcal{C}_{n}\rvert_{R\left[1/p\right]}\simeq \mathcal{D}_{F}^{-1}\otimes\mu_{p^{n}} \end{align*} $$
for the canonical subgroup
![]() $\mathcal {C}_{n}$
of A, and an isomorphism
$\mathcal {C}_{n}$
of A, and an isomorphism
satisfying the compatibility with u as before. By equality (3.1), any element
 $f\in H^{0}\left (\mathfrak {M}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )^{\mathrm {rig}}, \Omega ^{\kappa ^{\mathcal {U}}}\right )$
can be identified with a rule functorially associating, with any such tuple over R endowed with a map
$f\in H^{0}\left (\mathfrak {M}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )^{\mathrm {rig}}, \Omega ^{\kappa ^{\mathcal {U}}}\right )$
can be identified with a rule functorially associating, with any such tuple over R endowed with a map
![]() $\mathrm {Sp}(R[1/p])\to \mathcal {U}$
, an element
$\mathrm {Sp}(R[1/p])\to \mathcal {U}$
, an element
![]() $f(A,\iota ,\lambda ,\psi ,u,\alpha )$
of
$f(A,\iota ,\lambda ,\psi ,u,\alpha )$
of
![]() $R[1/p]$
satisfying
$R[1/p]$
satisfying
 $$ \begin{align*} f\left(A,\iota,\lambda,\psi,t^{-1}u,t^{-1}\alpha\right)=\kappa^{\mathcal{U}}(t) f(A,\iota,\lambda,\psi,u,\alpha) \end{align*} $$
$$ \begin{align*} f\left(A,\iota,\lambda,\psi,t^{-1}u,t^{-1}\alpha\right)=\kappa^{\mathcal{U}}(t) f(A,\iota,\lambda,\psi,u,\alpha) \end{align*} $$
for any
![]() $t\in \mathbb {T}\left (\mathbb {Z}_{p}\right )$
. Similarly, any element
$t\in \mathbb {T}\left (\mathbb {Z}_{p}\right )$
. Similarly, any element
 $f\in H^{0}\left (\mathfrak {M}(\mu _{N},\mathfrak {c})(0)^{\mathrm {rig}}, \Omega ^{\kappa ^{\mathcal {U}}}\right )$
has a similar description as a rule over any idyllic p-adic
$f\in H^{0}\left (\mathfrak {M}(\mu _{N},\mathfrak {c})(0)^{\mathrm {rig}}, \Omega ^{\kappa ^{\mathcal {U}}}\right )$
has a similar description as a rule over any idyllic p-adic
![]() $\mathcal {O}_{K}$
-algebra R endowed with a morphism
$\mathcal {O}_{K}$
-algebra R endowed with a morphism
![]() $\mathrm {Spf}(R)\to \bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)$
.
$\mathrm {Spf}(R)\to \bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)$
.
For later use, we also recall the definition of an integral structure of the sheaf
![]() $\Omega ^{\kappa ^{\mathcal {U}}}$
for an n-analytic map
$\Omega ^{\kappa ^{\mathcal {U}}}$
for an n-analytic map
![]() $\kappa ^{\mathcal {U}}: \mathcal {U}=\mathrm {Sp}(A)\to \mathcal {W}$
with some reduced K-affinoid algebra A. Note that
$\kappa ^{\mathcal {U}}: \mathcal {U}=\mathrm {Sp}(A)\to \mathcal {W}$
with some reduced K-affinoid algebra A. Note that
![]() $A^{\circ }$
is topologically of finite type [Reference Bosch, Güntzer and Remmert10, Corollary 6.4.1/6] and thus
$A^{\circ }$
is topologically of finite type [Reference Bosch, Güntzer and Remmert10, Corollary 6.4.1/6] and thus
![]() $\mathfrak {U}=\mathrm {Spf}(A^{\circ })$
is an admissible formal scheme over
$\mathfrak {U}=\mathrm {Spf}(A^{\circ })$
is an admissible formal scheme over
![]() $\mathrm {Spf}(\mathcal {O}_{K})$
. The map
$\mathrm {Spf}(\mathcal {O}_{K})$
. The map
![]() $\kappa ^{\mathcal {U}}$
extends to a formal character
$\kappa ^{\mathcal {U}}$
extends to a formal character
We put
 $$ \begin{align*} \mathbf{\Omega}^{\kappa^{\mathcal{U}}}=(\pi_{w})_{*}\left(\mathcal{O}_{\mathfrak{IW}_{w}^{+}\times \mathfrak{U}}\right)\left[-\boldsymbol{\kappa}^{\mathcal{U}}\right]. \end{align*} $$
$$ \begin{align*} \mathbf{\Omega}^{\kappa^{\mathcal{U}}}=(\pi_{w})_{*}\left(\mathcal{O}_{\mathfrak{IW}_{w}^{+}\times \mathfrak{U}}\right)\left[-\boldsymbol{\kappa}^{\mathcal{U}}\right]. \end{align*} $$
It is a coherent
![]() $\mathcal {O}_{\bar {\mathfrak {M}}\left (\mu _{N},\mathfrak {c}\right )\left (\underline {v}\right )\times \mathfrak {U}}$
-module which is independent of the choice of w such that its Raynaud generic fiber is
$\mathcal {O}_{\bar {\mathfrak {M}}\left (\mu _{N},\mathfrak {c}\right )\left (\underline {v}\right )\times \mathfrak {U}}$
-module which is independent of the choice of w such that its Raynaud generic fiber is
![]() $\Omega ^{\kappa ^{\mathcal {U}}}$
[Reference Andreatta, Iovita and Pilloni4, Proposition 3.13]. Since the map
$\Omega ^{\kappa ^{\mathcal {U}}}$
[Reference Andreatta, Iovita and Pilloni4, Proposition 3.13]. Since the map
![]() $h_{n}$
is an étale
$h_{n}$
is an étale
![]() $\mathbb {T}(\mathbb {Z}/p^{n}\mathbb {Z})$
-torsor over the ordinary locus
$\mathbb {T}(\mathbb {Z}/p^{n}\mathbb {Z})$
-torsor over the ordinary locus
![]() $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0) $
, the restriction of
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0) $
, the restriction of
![]() $\mathbf {\Omega }^{\kappa ^{\mathcal {U}}}$
to
$\mathbf {\Omega }^{\kappa ^{\mathcal {U}}}$
to
![]() $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)\times \mathfrak {U}$
is an invertible sheaf.
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)\times \mathfrak {U}$
is an invertible sheaf.
Let
![]() $\kappa :\mathbb {T}\left (\mathbb {Z}_{p}\right )\to K^{\times }$
be a weight character which is integral – namely, it is written as
$\kappa :\mathbb {T}\left (\mathbb {Z}_{p}\right )\to K^{\times }$
be a weight character which is integral – namely, it is written as
 $$ \begin{align*} \mathbb{T}\left(\mathbb{Z}_{p}\right)=\left(\mathcal{O}_{F}\otimes \mathbb{Z}_{p}\right)^{\times} \ni t\otimes 1\mapsto \prod_{\beta\in \mathbb{B}_{F}}\beta(t)^{k_{\beta}} \in K^{\times} \end{align*} $$
$$ \begin{align*} \mathbb{T}\left(\mathbb{Z}_{p}\right)=\left(\mathcal{O}_{F}\otimes \mathbb{Z}_{p}\right)^{\times} \ni t\otimes 1\mapsto \prod_{\beta\in \mathbb{B}_{F}}\beta(t)^{k_{\beta}} \in K^{\times} \end{align*} $$
with some g-tuple of integers
 $\left (k_{\beta }\right )_{\beta \in \mathbb {B}_{F}}$
. In this case, the sheaf
$\left (k_{\beta }\right )_{\beta \in \mathbb {B}_{F}}$
. In this case, the sheaf
![]() $\Omega ^{\kappa }$
is isomorphic to the classical automorphic sheaf [Reference Andreatta, Iovita and Pilloni4, Corollary 3.10]. Indeed, consider
$\Omega ^{\kappa }$
is isomorphic to the classical automorphic sheaf [Reference Andreatta, Iovita and Pilloni4, Corollary 3.10]. Indeed, consider
 $\mathcal {I}=\mathrm {Isom}_{\bar {\mathcal {M}}\left (\mu _{N},\mathfrak {c}\right )}\left (\mathcal {O}_{F}\otimes \mathcal {O}_{\bar {\mathcal {M}}\left (\mu _{N},\mathfrak {c}\right )}, \omega _{\bar {\mathcal {A}}^{\mathrm {un}}}\right )$
. Since the Raynaud generic fiber of the sheaf
$\mathcal {I}=\mathrm {Isom}_{\bar {\mathcal {M}}\left (\mu _{N},\mathfrak {c}\right )}\left (\mathcal {O}_{F}\otimes \mathcal {O}_{\bar {\mathcal {M}}\left (\mu _{N},\mathfrak {c}\right )}, \omega _{\bar {\mathcal {A}}^{\mathrm {un}}}\right )$
. Since the Raynaud generic fiber of the sheaf
![]() $\mathcal {F}$
is
$\mathcal {F}$
is
![]() $\omega _{\bar {\mathcal {A}}^{\mathrm {un}}}$
, we have a natural map
$\omega _{\bar {\mathcal {A}}^{\mathrm {un}}}$
, we have a natural map
![]() $\mathcal {IW}_{w}^{+}\to \mathcal {I}$
, which induces an isomorphism
$\mathcal {IW}_{w}^{+}\to \mathcal {I}$
, which induces an isomorphism
![]() $\omega _{\bar {\mathcal {A}} {}^{\mathrm {un}}}^{\kappa }\to \Omega ^{\kappa }$
. We also say that an integral weight
$\omega _{\bar {\mathcal {A}} {}^{\mathrm {un}}}^{\kappa }\to \Omega ^{\kappa }$
. We also say that an integral weight
![]() $\kappa $
is doubly even if every
$\kappa $
is doubly even if every
![]() $k_{\beta }$
is divisible by
$k_{\beta }$
is divisible by
![]() $4$
.
$4$
.
Moreover, we say that a weight character
![]() $\kappa :\mathbb {T}\left (\mathbb {Z}_{p}\right )\to K^{\times }$
is n-integral (resp., n-doubly even) if its restriction to
$\kappa :\mathbb {T}\left (\mathbb {Z}_{p}\right )\to K^{\times }$
is n-integral (resp., n-doubly even) if its restriction to
![]() $\mathbb {T}^{0}_{n}\left (\mathbb {Z}_{p}\right )$
is equal to the restriction of a character of some integral (resp., doubly even) weight
$\mathbb {T}^{0}_{n}\left (\mathbb {Z}_{p}\right )$
is equal to the restriction of a character of some integral (resp., doubly even) weight
 $\left (k_{\beta }\right )_{\beta \in \mathbb {B}_{F}}$
. Then, from the construction of the sheaf
$\left (k_{\beta }\right )_{\beta \in \mathbb {B}_{F}}$
. Then, from the construction of the sheaf
![]() $\Omega ^{\kappa }$
, we see that the pullback
$\Omega ^{\kappa }$
, we see that the pullback
 $\left (h^{\mathrm {rig}}_{n}\right )^{*}\Omega ^{\kappa }$
to
$\left (h^{\mathrm {rig}}_{n}\right )^{*}\Omega ^{\kappa }$
to
![]() $\bar {\mathcal {M}}(\Gamma _{1}(p^{n}),\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
is isomorphic to
$\bar {\mathcal {M}}(\Gamma _{1}(p^{n}),\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
is isomorphic to
 $\left (h^{\mathrm {rig}}_{n}\right )^{*} \left (\bigotimes _{\beta \in \mathbb {B}_{F}} \omega ^{\otimes k_{\beta }}_{\bar {\mathcal {A}}^{\mathrm {un}},\beta }\right )$
. Note that for the case where
$\left (h^{\mathrm {rig}}_{n}\right )^{*} \left (\bigotimes _{\beta \in \mathbb {B}_{F}} \omega ^{\otimes k_{\beta }}_{\bar {\mathcal {A}}^{\mathrm {un}},\beta }\right )$
. Note that for the case where
![]() $p=2$
splits completely in F, a
$p=2$
splits completely in F, a
![]() $1$
-integral weight is
$1$
-integral weight is
![]() $1$
-analytic if and only if it is
$1$
-analytic if and only if it is
![]() $1$
-doubly even.
$1$
-doubly even.
3.3.2 Overconvergent arithmetic Hilbert modular forms
We define the weight space
![]() $\mathcal {W}^{G}$
for overconvergent Hilbert modular forms as the Berthelot generic fiber of
$\mathcal {W}^{G}$
for overconvergent Hilbert modular forms as the Berthelot generic fiber of
 $\mathrm {Spf}\left (\mathcal {O}_{K}\left [\left [\mathbb {T}\left (\mathbb {Z}_{p}\right )\times \mathbb {Z}_{p}^{\times }\right ]\right ]\right )$
. Any morphism
$\mathrm {Spf}\left (\mathcal {O}_{K}\left [\left [\mathbb {T}\left (\mathbb {Z}_{p}\right )\times \mathbb {Z}_{p}^{\times }\right ]\right ]\right )$
. Any morphism
![]() $\mathcal {X}\to \mathcal {W}^{G}$
defines a pair
$\mathcal {X}\to \mathcal {W}^{G}$
defines a pair
 $\left (\nu ^{\mathcal {X}}, w^{\mathcal {X}}\right )$
of continuous characters
$\left (\nu ^{\mathcal {X}}, w^{\mathcal {X}}\right )$
of continuous characters
 $$ \begin{align*} \nu^{\mathcal{X}}: \mathbb{T}\left(\mathbb{Z}_{p}\right)\to \mathcal{O}^{\circ}(\mathcal{X})^{\times},\qquad w^{\mathcal{X}}:\mathbb{Z}_{p}^{\times} \to \mathcal{O}^{\circ}(\mathcal{X})^{\times} \end{align*} $$
$$ \begin{align*} \nu^{\mathcal{X}}: \mathbb{T}\left(\mathbb{Z}_{p}\right)\to \mathcal{O}^{\circ}(\mathcal{X})^{\times},\qquad w^{\mathcal{X}}:\mathbb{Z}_{p}^{\times} \to \mathcal{O}^{\circ}(\mathcal{X})^{\times} \end{align*} $$
with respect to the supremum seminorm on
![]() $\mathcal {X}$
. The map
$\mathcal {X}$
. The map
 $$ \begin{align*} \mathbb{T}\left(\mathbb{Z}_{p}\right)\to \mathbb{T}\left(\mathbb{Z}_{p}\right)\times \mathbb{Z}_{p}^{\times},\quad t\mapsto \left(t^{2}, \mathrm{N}_{F/\mathbb{Q}}(t)\right), \end{align*} $$
$$ \begin{align*} \mathbb{T}\left(\mathbb{Z}_{p}\right)\to \mathbb{T}\left(\mathbb{Z}_{p}\right)\times \mathbb{Z}_{p}^{\times},\quad t\mapsto \left(t^{2}, \mathrm{N}_{F/\mathbb{Q}}(t)\right), \end{align*} $$
induces a morphism
![]() $k: \mathcal {W}^{G}\to \mathcal {W}$
. For any morphism
$k: \mathcal {W}^{G}\to \mathcal {W}$
. For any morphism
![]() $\mathcal {X}\to \mathcal {W}^{G}$
, put
$\mathcal {X}\to \mathcal {W}^{G}$
, put
 $\kappa ^{\mathcal {X}}=k\left (\nu ^{\mathcal {X}},w^{\mathcal {X}}\right )$
. When
$\kappa ^{\mathcal {X}}=k\left (\nu ^{\mathcal {X}},w^{\mathcal {X}}\right )$
. When
![]() $\mathcal {X}$
is a reduced K-affinoid variety, we say that
$\mathcal {X}$
is a reduced K-affinoid variety, we say that
 $\left (\nu ^{\mathcal {X}},w^{\mathcal {X}}\right )$
is n-analytic if
$\left (\nu ^{\mathcal {X}},w^{\mathcal {X}}\right )$
is n-analytic if
![]() $\nu ^{\mathcal {X}}$
and
$\nu ^{\mathcal {X}}$
and
![]() $w^{\mathcal {X}}$
are both n-analytic. Note that if
$w^{\mathcal {X}}$
are both n-analytic. Note that if
 $\left (\nu ^{\mathcal {X}},w^{\mathcal {X}}\right )$
is n-analytic, then
$\left (\nu ^{\mathcal {X}},w^{\mathcal {X}}\right )$
is n-analytic, then
![]() $\kappa ^{\mathcal {X}}$
is also n-analytic. We say that a character
$\kappa ^{\mathcal {X}}$
is also n-analytic. We say that a character
![]() $(\nu ,w): \mathbb {T}\left (\mathbb {Z}_{p}\right )\times \mathbb {Z}_{p}^{\times }\to K^{\times }$
is integral if it comes from an algebraic character
$(\nu ,w): \mathbb {T}\left (\mathbb {Z}_{p}\right )\times \mathbb {Z}_{p}^{\times }\to K^{\times }$
is integral if it comes from an algebraic character
![]() $\mathbb {T}\times \mathbb {G}_{\mathrm {m}}\to \mathbb {G}_{\mathrm {m}}$
. Then it is written as
$\mathbb {T}\times \mathbb {G}_{\mathrm {m}}\to \mathbb {G}_{\mathrm {m}}$
. Then it is written as
 $$ \begin{align*} \mathbb{T}\left(\mathbb{Z}_{p}\right)\times \mathbb{Z}_{p}^{\times}\to K^{\times},\quad (t\otimes 1,s)\mapsto \prod_{\beta\in \mathbb{B}_{F}} \beta(t)^{k_{\beta}}s^{k_{0}}, \end{align*} $$
$$ \begin{align*} \mathbb{T}\left(\mathbb{Z}_{p}\right)\times \mathbb{Z}_{p}^{\times}\to K^{\times},\quad (t\otimes 1,s)\mapsto \prod_{\beta\in \mathbb{B}_{F}} \beta(t)^{k_{\beta}}s^{k_{0}}, \end{align*} $$
with some g-tuple of integers
 $\left (k_{\beta }\right )_{\beta \in \mathbb {B}_{F}}$
and an integer
$\left (k_{\beta }\right )_{\beta \in \mathbb {B}_{F}}$
and an integer
![]() $k_{0}$
. We say that it is doubly even if every
$k_{0}$
. We say that it is doubly even if every
![]() $k_{\beta }$
and
$k_{\beta }$
and
![]() $k_{0}$
are divisible by
$k_{0}$
are divisible by
![]() $4$
. We also say that
$4$
. We also say that
![]() $(\nu ,w)$
is n-integral (resp., n-doubly even) if its restriction to
$(\nu ,w)$
is n-integral (resp., n-doubly even) if its restriction to
![]() $\mathbb {T}^{0}_{n}\left (\mathbb {Z}_{p}\right )\times \left (1+p^{n}\mathbb {Z}_{p}\right )$
is equal to the restriction of some integral (resp., doubly even) character. If
$\mathbb {T}^{0}_{n}\left (\mathbb {Z}_{p}\right )\times \left (1+p^{n}\mathbb {Z}_{p}\right )$
is equal to the restriction of some integral (resp., doubly even) character. If
![]() $(\nu ,w)$
is n-integral (resp., n-doubly even), then
$(\nu ,w)$
is n-integral (resp., n-doubly even), then
![]() $k(\nu ,w)$
is also n-integral (resp., n-doubly even).
$k(\nu ,w)$
is also n-integral (resp., n-doubly even).
Let
![]() $\mathcal {U}$
be a reduced K-affinoid variety and let
$\mathcal {U}$
be a reduced K-affinoid variety and let
![]() $\mathcal {U}\to \mathcal {W}^{G}$
be an n-analytic morphism. Note that for any
$\mathcal {U}\to \mathcal {W}^{G}$
be an n-analytic morphism. Note that for any
![]() $\mathfrak {c}$
-polarization
$\mathfrak {c}$
-polarization
![]() $\lambda : A\otimes _{\mathcal {O}_{F}} \mathfrak {c}\to A^{\vee }$
and any
$\lambda : A\otimes _{\mathcal {O}_{F}} \mathfrak {c}\to A^{\vee }$
and any
![]() $x\in F^{\times ,+}$
, multiplication by x gives an
$x\in F^{\times ,+}$
, multiplication by x gives an
![]() $x^{-1}\mathfrak {c}$
-polarization
$x^{-1}\mathfrak {c}$
-polarization
 $$ \begin{align*} x\lambda: A\otimes_{\mathcal{O}_{F}} x^{-1}\mathfrak{c}\overset{\times x}{\simeq} A\otimes_{\mathcal{O}_{F}} \mathfrak{c}\overset{\lambda}{\simeq} A^{\vee}. \end{align*} $$
$$ \begin{align*} x\lambda: A\otimes_{\mathcal{O}_{F}} x^{-1}\mathfrak{c}\overset{\times x}{\simeq} A\otimes_{\mathcal{O}_{F}} \mathfrak{c}\overset{\lambda}{\simeq} A^{\vee}. \end{align*} $$
Then the group
 $\Delta =\mathcal {O}_{F}^{\times ,+}/U_{N}^{2}$
acts on the space
$\Delta =\mathcal {O}_{F}^{\times ,+}/U_{N}^{2}$
acts on the space
 $M\left (\mu _{N}, \mathfrak {c}, \kappa ^{\mathcal {U}}\right )\left (\underline {v}\right )$
by
$M\left (\mu _{N}, \mathfrak {c}, \kappa ^{\mathcal {U}}\right )\left (\underline {v}\right )$
by
 $$ \begin{align*} ([\epsilon].f)(A,\iota,\lambda,\psi, u,\alpha)=\nu^{\mathcal{U}}(\epsilon)f\left(A,\iota,\epsilon^{-1}\lambda,\psi, u,\alpha\right) \end{align*} $$
$$ \begin{align*} ([\epsilon].f)(A,\iota,\lambda,\psi, u,\alpha)=\nu^{\mathcal{U}}(\epsilon)f\left(A,\iota,\epsilon^{-1}\lambda,\psi, u,\alpha\right) \end{align*} $$
for any
 $f\in M\left (\mu _{N}, \mathfrak {c}, \kappa ^{\mathcal {U}}\right )\left (\underline {v}\right )$
and
$f\in M\left (\mu _{N}, \mathfrak {c}, \kappa ^{\mathcal {U}}\right )\left (\underline {v}\right )$
and
 $\epsilon \in \mathcal {O}_{F}^{\times ,+}$
. We define
$\epsilon \in \mathcal {O}_{F}^{\times ,+}$
. We define
 $$ \begin{align*} M^{G}\left(\mu_{N},\mathfrak{c}, \left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)\left(\underline{v}\right)&=M\left(\mu_{N}, \mathfrak{c}, \kappa^{\mathcal{U}}\right)\left(\underline{v}\right)^{\Delta},\\ S^{G}\left(\mu_{N},\mathfrak{c}, \left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)\left(\underline{v}\right)&=S\left(\mu_{N}, \mathfrak{c}, \kappa^{\mathcal{U}}\right)\left(\underline{v}\right)^{\Delta}. \end{align*} $$
$$ \begin{align*} M^{G}\left(\mu_{N},\mathfrak{c}, \left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)\left(\underline{v}\right)&=M\left(\mu_{N}, \mathfrak{c}, \kappa^{\mathcal{U}}\right)\left(\underline{v}\right)^{\Delta},\\ S^{G}\left(\mu_{N},\mathfrak{c}, \left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)\left(\underline{v}\right)&=S\left(\mu_{N}, \mathfrak{c}, \kappa^{\mathcal{U}}\right)\left(\underline{v}\right)^{\Delta}. \end{align*} $$
Let
![]() $F^{\times , +,(p)}$
be the subgroup of
$F^{\times , +,(p)}$
be the subgroup of
![]() $F^{\times ,+}$
consisting of p-adic units. For any
$F^{\times ,+}$
consisting of p-adic units. For any
![]() $x\in F^{\times ,+,(p)}$
, we define a map
$x\in F^{\times ,+,(p)}$
, we define a map
 $$ \begin{align*} L_{x}: M^{G}\left(\mu_{N},\mathfrak{c}, \left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)\left(\underline{v}\right) \to M^{G}\left(\mu_{N},x^{-1}\mathfrak{c}, \left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)\left(\underline{v}\right) \end{align*} $$
$$ \begin{align*} L_{x}: M^{G}\left(\mu_{N},\mathfrak{c}, \left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)\left(\underline{v}\right) \to M^{G}\left(\mu_{N},x^{-1}\mathfrak{c}, \left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)\left(\underline{v}\right) \end{align*} $$
by the formula
 $$ \begin{align*} (L_{x}(f))(A,\iota,\lambda,\psi,u,\alpha)=\nu^{\mathcal{U}}(x) f\left(A,\iota, x^{-1}\lambda,\psi,u,\alpha\right). \end{align*} $$
$$ \begin{align*} (L_{x}(f))(A,\iota,\lambda,\psi,u,\alpha)=\nu^{\mathcal{U}}(x) f\left(A,\iota, x^{-1}\lambda,\psi,u,\alpha\right). \end{align*} $$
Let
![]() $\mathrm {Frac}(F)^{(p)}$
be the group of fractional ideals of F which are prime to p. Then the spaces
$\mathrm {Frac}(F)^{(p)}$
be the group of fractional ideals of F which are prime to p. Then the spaces
 $$ \begin{align*} M^{G}\left(\mu_{N}, \left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)\left(\underline{v}\right),\qquad S^{G}\left(\mu_{N}, \left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)\left(\underline{v}\right) \end{align*} $$
$$ \begin{align*} M^{G}\left(\mu_{N}, \left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)\left(\underline{v}\right),\qquad S^{G}\left(\mu_{N}, \left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)\left(\underline{v}\right) \end{align*} $$
of arithmetic overconvergent Hilbert modular forms and cusp forms are defined as the quotients
 $$ \begin{align*} &\left(\bigoplus_{\mathfrak{c}\in \mathrm{Frac}(F)^{\left(p\right)}} M^{G}\left(\mu_{N},\mathfrak{c}, \left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)\left(\underline{v}\right)\right)/\left(L_{x}(f)-f\mid x\in F^{\times, +,(p)}\right),\\ &\left(\bigoplus_{\mathfrak{c}\in \mathrm{Frac}(F)^{\left(p\right)}} S^{G}\left(\mu_{N},\mathfrak{c}, \left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)\left(\underline{v}\right)\right)/\left(L_{x}(f)-f\mid x\in F^{\times, +,(p)}\right). \end{align*} $$
$$ \begin{align*} &\left(\bigoplus_{\mathfrak{c}\in \mathrm{Frac}(F)^{\left(p\right)}} M^{G}\left(\mu_{N},\mathfrak{c}, \left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)\left(\underline{v}\right)\right)/\left(L_{x}(f)-f\mid x\in F^{\times, +,(p)}\right),\\ &\left(\bigoplus_{\mathfrak{c}\in \mathrm{Frac}(F)^{\left(p\right)}} S^{G}\left(\mu_{N},\mathfrak{c}, \left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)\left(\underline{v}\right)\right)/\left(L_{x}(f)-f\mid x\in F^{\times, +,(p)}\right). \end{align*} $$
By the same construction, we also have the spaces
 $$ \begin{align*} M^{G}\left(\mu_{N}, \left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)(v_{\mathrm{tot}}),\qquad S^{G}\left(\mu_{N}, \left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)(v_{\mathrm{tot}}). \end{align*} $$
$$ \begin{align*} M^{G}\left(\mu_{N}, \left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)(v_{\mathrm{tot}}),\qquad S^{G}\left(\mu_{N}, \left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)(v_{\mathrm{tot}}). \end{align*} $$
3.3.3 Hecke operators and the Hilbert eigenvariety
Next we recall the definition of Hecke operators on the space of overconvergent Hilbert modular forms, following [Reference Andreatta, Iovita and Pilloni4, §3.7]. Let n,
![]() $\underline {v}$
, v, and w be as before. For any HBAV
$\underline {v}$
, v, and w be as before. For any HBAV
![]() $(A,\iota ,\lambda ,\psi )$
over a base scheme
$(A,\iota ,\lambda ,\psi )$
over a base scheme
![]() $S/\mathrm {Spec}(\mathcal {O}_{K})$
, the closed immersion
$S/\mathrm {Spec}(\mathcal {O}_{K})$
, the closed immersion
 $\psi : \mathcal {D}^{-1}_{F}\otimes \mu _{N} \to A$
gives a subgroup scheme
$\psi : \mathcal {D}^{-1}_{F}\otimes \mu _{N} \to A$
gives a subgroup scheme
![]() $\mathrm {Im}(\psi )$
of A which is étale locally isomorphic to
$\mathrm {Im}(\psi )$
of A which is étale locally isomorphic to
 $\underline {\mathcal {D}_{F}^{-1}/N\mathcal {D}_{F}^{-1}}$
. Let
$\underline {\mathcal {D}_{F}^{-1}/N\mathcal {D}_{F}^{-1}}$
. Let
![]() $\mathfrak {l}$
be any nonzero ideal of
$\mathfrak {l}$
be any nonzero ideal of
![]() $\mathcal {O}_{F}$
. We define
$\mathcal {O}_{F}$
. We define
 $$ \begin{align*} \mathcal{Y}^{\prime}_{\mathfrak{c},\mathfrak{l}}\left(\underline{v}\right)\subseteq \mathcal{M}(\mu_{N},\mathfrak{c})\left(\underline{v}\right)\times \mathcal{M}(\mu_{N},\mathfrak{l}\mathfrak{c})\left(\underline{v}\right) \end{align*} $$
$$ \begin{align*} \mathcal{Y}^{\prime}_{\mathfrak{c},\mathfrak{l}}\left(\underline{v}\right)\subseteq \mathcal{M}(\mu_{N},\mathfrak{c})\left(\underline{v}\right)\times \mathcal{M}(\mu_{N},\mathfrak{l}\mathfrak{c})\left(\underline{v}\right) \end{align*} $$
as the subvariety classifying pairs
![]() $((A,\iota ,\lambda ,\psi ),(A^{\prime },\iota ^{\prime },\lambda ^{\prime },\psi ^{\prime }))$
and an isogeny
$((A,\iota ,\lambda ,\psi ),(A^{\prime },\iota ^{\prime },\lambda ^{\prime },\psi ^{\prime }))$
and an isogeny
![]() $\pi _{\mathfrak {l}}:A\to A^{\prime }$
compatible with the other data such that
$\pi _{\mathfrak {l}}:A\to A^{\prime }$
compatible with the other data such that
![]() $\mathrm {Ker}(\pi _{\mathfrak {l}})$
is étale locally isomorphic to
$\mathrm {Ker}(\pi _{\mathfrak {l}})$
is étale locally isomorphic to
![]() $\underline {\mathcal {O}_{F}/\mathfrak {l} \mathcal {O}_{F}}$
,
$\underline {\mathcal {O}_{F}/\mathfrak {l} \mathcal {O}_{F}}$
,
![]() $\mathrm {Ker}(\pi _{\mathfrak {l}})\cap \mathrm {Im}(\psi )=0$
, and
$\mathrm {Ker}(\pi _{\mathfrak {l}})\cap \mathrm {Im}(\psi )=0$
, and
![]() $\mathrm {Ker}(\pi _{\mathfrak {l}})\cap C_{1}=0$
, where
$\mathrm {Ker}(\pi _{\mathfrak {l}})\cap C_{1}=0$
, where
![]() $C_{1}$
is the canonical subgroup of A of level
$C_{1}$
is the canonical subgroup of A of level
![]() $1$
. Consider the projections
$1$
. Consider the projections
 $$ \begin{align*} p_{1}: \mathcal{Y}^{\prime}_{\mathfrak{c},\mathfrak{l}}\left(\underline{v}\right)\to \mathcal{M}(\mu_{N},\mathfrak{c})\left(\underline{v}\right),\qquad p_{2}: \mathcal{Y}^{\prime}_{\mathfrak{c},\mathfrak{l}}\left(\underline{v}\right)\to \mathcal{M}(\mu_{N},\mathfrak{l}\mathfrak{c})\left(\underline{v}\right). \end{align*} $$
$$ \begin{align*} p_{1}: \mathcal{Y}^{\prime}_{\mathfrak{c},\mathfrak{l}}\left(\underline{v}\right)\to \mathcal{M}(\mu_{N},\mathfrak{c})\left(\underline{v}\right),\qquad p_{2}: \mathcal{Y}^{\prime}_{\mathfrak{c},\mathfrak{l}}\left(\underline{v}\right)\to \mathcal{M}(\mu_{N},\mathfrak{l}\mathfrak{c})\left(\underline{v}\right). \end{align*} $$
Note that map
![]() $p_{1}$
is finite and étale. For the case where
$p_{1}$
is finite and étale. For the case where
![]() $\mathfrak {l}$
is a prime ideal dividing p, we suppose that
$\mathfrak {l}$
is a prime ideal dividing p, we suppose that
![]() $p^{-1}v_{\sigma \circ \beta }\leq v_{\beta }$
for any
$p^{-1}v_{\sigma \circ \beta }\leq v_{\beta }$
for any
![]() $\beta \in \mathbb {B}_{\mathfrak {l}}$
. Set
$\beta \in \mathbb {B}_{\mathfrak {l}}$
. Set
 $\underline {v}^{\prime }=\left (v^{\prime }_{\beta }\right )_{\beta \in \mathbb {B}_{F}}$
by
$\underline {v}^{\prime }=\left (v^{\prime }_{\beta }\right )_{\beta \in \mathbb {B}_{F}}$
by
 $v^{\prime }_{\beta }=v_{\beta }$
for
$v^{\prime }_{\beta }=v_{\beta }$
for
![]() $\beta \notin \mathbb {B}_{\mathfrak {l}}$
and
$\beta \notin \mathbb {B}_{\mathfrak {l}}$
and
 $v^{\prime }_{\beta }=p^{-1}v_{\sigma \circ \beta }$
for
$v^{\prime }_{\beta }=p^{-1}v_{\sigma \circ \beta }$
for
![]() $\beta \in \mathbb {B}_{\mathfrak {l}}$
. Then [Reference Hattori29, Corollary 5.3(1)] implies that map
$\beta \in \mathbb {B}_{\mathfrak {l}}$
. Then [Reference Hattori29, Corollary 5.3(1)] implies that map
![]() $p_{2}$
factors through the admissible open subset
$p_{2}$
factors through the admissible open subset
![]() $\mathcal {M}(\mu _{N},\mathfrak {l}\mathfrak {c})\left (\underline {v}^{\prime }\right )\subseteq \mathcal {M}(\mu _{N},\mathfrak {l}\mathfrak {c})\left (\underline {v}\right )$
.
$\mathcal {M}(\mu _{N},\mathfrak {l}\mathfrak {c})\left (\underline {v}^{\prime }\right )\subseteq \mathcal {M}(\mu _{N},\mathfrak {l}\mathfrak {c})\left (\underline {v}\right )$
.
Let
![]() $\mathcal {U}$
be a smooth K-affinoid variety and let
$\mathcal {U}$
be a smooth K-affinoid variety and let
![]() $\mathcal {U}\to \mathcal {W}$
be an n-analytic map. Then [Reference Hattori29, Theorem 8.1(10)] and the proof of [Reference Andreatta, Iovita and Pilloni4, Corollary 3.26] (see also [Reference Andreatta, Iovita and Pilloni3, Lemma 6.1.1]) show that the map
$\mathcal {U}\to \mathcal {W}$
be an n-analytic map. Then [Reference Hattori29, Theorem 8.1(10)] and the proof of [Reference Andreatta, Iovita and Pilloni4, Corollary 3.26] (see also [Reference Andreatta, Iovita and Pilloni3, Lemma 6.1.1]) show that the map
![]() $\pi _{\mathfrak {l}}^{*}: \omega _{A^{\prime }}\to \omega _{A}$
induces an isomorphism
$\pi _{\mathfrak {l}}^{*}: \omega _{A^{\prime }}\to \omega _{A}$
induces an isomorphism
 $$ \begin{align*} \pi_{\mathfrak{l}}: p_{2}^{*} \mathcal{IW}_{w,\mathfrak{l} \mathfrak{c}}^{+}\left(\underline{v}\right) \simeq p_{1}^{*}\mathcal{IW}_{w,\mathfrak{c}}^{+}\left(\underline{v}\right), \end{align*} $$
$$ \begin{align*} \pi_{\mathfrak{l}}: p_{2}^{*} \mathcal{IW}_{w,\mathfrak{l} \mathfrak{c}}^{+}\left(\underline{v}\right) \simeq p_{1}^{*}\mathcal{IW}_{w,\mathfrak{c}}^{+}\left(\underline{v}\right), \end{align*} $$
which in turn defines an isomorphism
 $$ \begin{align*} \pi_{\mathfrak{l}}^{*}: p_{1}^{*}\left(\Omega^{\kappa^{\mathcal{U}}}\right)\simeq p_{2}^{*}\left(\Omega^{\kappa^{\mathcal{U}}}\right). \end{align*} $$
$$ \begin{align*} \pi_{\mathfrak{l}}^{*}: p_{1}^{*}\left(\Omega^{\kappa^{\mathcal{U}}}\right)\simeq p_{2}^{*}\left(\Omega^{\kappa^{\mathcal{U}}}\right). \end{align*} $$
This gives the Hecke operator
 $$ \begin{align*} H^{0}\left(\mathcal{M}(\mu_{N},\mathfrak{l}\mathfrak{c})\left(\underline{v}\right)\times \mathcal{U},\Omega^{\kappa^{\mathcal{U}}}\right) & \overset{p_{2}^{*}}{\to} H^{0}\left(\mathcal{Y}^{\prime}_{\mathfrak{c},\mathfrak{l}}\left(\underline{v}\right)\times \mathcal{U},p_{2}^{*}\Omega^{\kappa^{\mathcal{U}}}\right)\\ & \overset{\left(\pi_{\mathfrak{l}}^{*}\right)^{-1}}{\to} H^{0}\left(\mathcal{Y}^{\prime}_{\mathfrak{c}, \mathfrak{l}}\left(\underline{v}\right)\times \mathcal{U},p_{1}^{*}\Omega^{\kappa^{\mathcal{U}}}\right)\\ & \overset{\mathrm{N}_{F/\mathbb{Q}}(\mathfrak{l})^{-1}\mathrm{Tr}_{p_{1}}}{\to} H^{0}\left(\mathcal{M}(\mu_{N},\mathfrak{c})\left(\underline{v}\right)\times \mathcal{U},\Omega^{\kappa^{\mathcal{U}}}\right), \end{align*} $$
$$ \begin{align*} H^{0}\left(\mathcal{M}(\mu_{N},\mathfrak{l}\mathfrak{c})\left(\underline{v}\right)\times \mathcal{U},\Omega^{\kappa^{\mathcal{U}}}\right) & \overset{p_{2}^{*}}{\to} H^{0}\left(\mathcal{Y}^{\prime}_{\mathfrak{c},\mathfrak{l}}\left(\underline{v}\right)\times \mathcal{U},p_{2}^{*}\Omega^{\kappa^{\mathcal{U}}}\right)\\ & \overset{\left(\pi_{\mathfrak{l}}^{*}\right)^{-1}}{\to} H^{0}\left(\mathcal{Y}^{\prime}_{\mathfrak{c}, \mathfrak{l}}\left(\underline{v}\right)\times \mathcal{U},p_{1}^{*}\Omega^{\kappa^{\mathcal{U}}}\right)\\ & \overset{\mathrm{N}_{F/\mathbb{Q}}(\mathfrak{l})^{-1}\mathrm{Tr}_{p_{1}}}{\to} H^{0}\left(\mathcal{M}(\mu_{N},\mathfrak{c})\left(\underline{v}\right)\times \mathcal{U},\Omega^{\kappa^{\mathcal{U}}}\right), \end{align*} $$
which can be seen as a map
 $M\left (\mu _{N},\mathfrak {l}\mathfrak {c},\kappa ^{\mathcal {U}}\right )\left (\underline {v}\right )\to M\left (\mu _{N},\mathfrak {c},\kappa ^{\mathcal {U}}\right )\left (\underline {v}\right )$
by [Reference Lütkebohmert33, Theorem 1.6]. We denote this map by
$M\left (\mu _{N},\mathfrak {l}\mathfrak {c},\kappa ^{\mathcal {U}}\right )\left (\underline {v}\right )\to M\left (\mu _{N},\mathfrak {c},\kappa ^{\mathcal {U}}\right )\left (\underline {v}\right )$
by [Reference Lütkebohmert33, Theorem 1.6]. We denote this map by
![]() $T_{\mathfrak {l}}$
if
$T_{\mathfrak {l}}$
if
![]() $(\mathfrak {l},p)=1$
and
$(\mathfrak {l},p)=1$
and
![]() $T^{\prime }_{\mathfrak {l}}$
otherwise.
$T^{\prime }_{\mathfrak {l}}$
otherwise.
On the other hand, for any ideal
![]() $\mathfrak {l}$
with
$\mathfrak {l}$
with
![]() $(\mathfrak {l},pN)=1$
, we have a map
$(\mathfrak {l},pN)=1$
, we have a map
 $$ \begin{align*} s_{\mathfrak{l}}: \mathcal{M}(\mu_{N},\mathfrak{c})\left(\underline{v}\right)\to \mathcal{M}\left(\mu_{N}, \mathfrak{l}^{2} \mathfrak{c}\right)\left(\underline{v}\right),\quad (A,\iota,\lambda,\psi)\mapsto \left(A\otimes_{\mathcal{O}_{F}} \mathfrak{l}^{-1}, \iota^{\prime},\mathfrak{l}^{2}\lambda, \psi^{\prime}\right). \end{align*} $$
$$ \begin{align*} s_{\mathfrak{l}}: \mathcal{M}(\mu_{N},\mathfrak{c})\left(\underline{v}\right)\to \mathcal{M}\left(\mu_{N}, \mathfrak{l}^{2} \mathfrak{c}\right)\left(\underline{v}\right),\quad (A,\iota,\lambda,\psi)\mapsto \left(A\otimes_{\mathcal{O}_{F}} \mathfrak{l}^{-1}, \iota^{\prime},\mathfrak{l}^{2}\lambda, \psi^{\prime}\right). \end{align*} $$
Here
![]() $\iota ^{\prime }$
and
$\iota ^{\prime }$
and
![]() $\psi ^{\prime }$
are induced by
$\psi ^{\prime }$
are induced by
![]() $\iota $
and
$\iota $
and
![]() $\psi $
via the natural isogeny
$\psi $
via the natural isogeny
![]() $A\to A/A[\mathfrak {l}]\simeq A\otimes _{\mathcal {O}_{F}} \mathfrak {l}^{-1}$
, and
$A\to A/A[\mathfrak {l}]\simeq A\otimes _{\mathcal {O}_{F}} \mathfrak {l}^{-1}$
, and
![]() $\mathfrak {l}^{2}\lambda $
is the
$\mathfrak {l}^{2}\lambda $
is the
![]() $\mathfrak {l}^{2}\mathfrak {c}$
-polarization on
$\mathfrak {l}^{2}\mathfrak {c}$
-polarization on
![]() $A\otimes _{\mathcal {O}_{F}} \mathfrak {l}^{-1}$
defined by
$A\otimes _{\mathcal {O}_{F}} \mathfrak {l}^{-1}$
defined by
 $$ \begin{align*} \left(A\otimes_{\mathcal{O}_{F}} \mathfrak{l}^{-1}\right)\otimes_{\mathcal{O}_{F}} \mathfrak{l}^{2}\mathfrak{c} =\left(A\otimes {}_{\mathcal{O}_{F}}\mathfrak{c}\right)\otimes_{\mathcal{O}_{F}}\mathfrak{l}\overset{\lambda\otimes 1}{\simeq} A^{\vee}\otimes_{\mathcal{O}_{F}}\mathfrak{l}\simeq \left(A\otimes_{\mathcal{O}_{F}}\mathfrak{l}^{-1}\right)^{\vee}. \end{align*} $$
$$ \begin{align*} \left(A\otimes_{\mathcal{O}_{F}} \mathfrak{l}^{-1}\right)\otimes_{\mathcal{O}_{F}} \mathfrak{l}^{2}\mathfrak{c} =\left(A\otimes {}_{\mathcal{O}_{F}}\mathfrak{c}\right)\otimes_{\mathcal{O}_{F}}\mathfrak{l}\overset{\lambda\otimes 1}{\simeq} A^{\vee}\otimes_{\mathcal{O}_{F}}\mathfrak{l}\simeq \left(A\otimes_{\mathcal{O}_{F}}\mathfrak{l}^{-1}\right)^{\vee}. \end{align*} $$
Then we can show that there exists a natural isomorphism
 $\pi _{\mathfrak {l}}^{*}: \Omega ^{\kappa ^{\mathcal {U}}} \simeq s_{\mathfrak {l}}^{*} \Omega ^{\kappa ^{\mathcal {U}}}$
as in [Reference Andreatta, Iovita and Pilloni3, Lemma 6.1.1], and we define the operator
$\pi _{\mathfrak {l}}^{*}: \Omega ^{\kappa ^{\mathcal {U}}} \simeq s_{\mathfrak {l}}^{*} \Omega ^{\kappa ^{\mathcal {U}}}$
as in [Reference Andreatta, Iovita and Pilloni3, Lemma 6.1.1], and we define the operator
 $$ \begin{align*} S_{\mathfrak{l}}: M\left(\mu_{N},\mathfrak{l}^{2}\mathfrak{c},\kappa^{\mathcal{U}}\right)\left(\underline{v}\right)\to M\left(\mu_{N},\mathfrak{c},\kappa^{\mathcal{U}}\right)\left(\underline{v}\right) \end{align*} $$
$$ \begin{align*} S_{\mathfrak{l}}: M\left(\mu_{N},\mathfrak{l}^{2}\mathfrak{c},\kappa^{\mathcal{U}}\right)\left(\underline{v}\right)\to M\left(\mu_{N},\mathfrak{c},\kappa^{\mathcal{U}}\right)\left(\underline{v}\right) \end{align*} $$
by
 $S_{\mathfrak {l}}=\mathrm {N}_{F/\mathbb {Q}}(\mathfrak {l})^{-2}\left (\pi _{\mathfrak {l}}^{*}\right )^{-1}\circ s_{\mathfrak {l}}^{*}$
. Since
$S_{\mathfrak {l}}=\mathrm {N}_{F/\mathbb {Q}}(\mathfrak {l})^{-2}\left (\pi _{\mathfrak {l}}^{*}\right )^{-1}\circ s_{\mathfrak {l}}^{*}$
. Since
![]() $s_{\mathfrak {l}}^{m}=\mathrm {id}$
for some positive integer m, every eigenvalue of the operator
$s_{\mathfrak {l}}^{m}=\mathrm {id}$
for some positive integer m, every eigenvalue of the operator
![]() $S_{\mathfrak {l}}$
is p-integral.
$S_{\mathfrak {l}}$
is p-integral.
To define arithmetic Hecke operators for
![]() $\mathfrak {l}$
with
$\mathfrak {l}$
with
![]() $(\mathfrak {l},p)\neq 1$
, let
$(\mathfrak {l},p)\neq 1$
, let
![]() $v_{\mathfrak {p}}$
be the normalized additive valuation for any
$v_{\mathfrak {p}}$
be the normalized additive valuation for any
![]() $\mathfrak {p}\mid p$
. We fix once and for all elements
$\mathfrak {p}\mid p$
. We fix once and for all elements
![]() $x_{\mathfrak {p}}\in F^{\times ,+}$
such that
$x_{\mathfrak {p}}\in F^{\times ,+}$
such that
![]() $v_{\mathfrak {p}}\left (x_{\mathfrak {p}}\right )=1$
and
$v_{\mathfrak {p}}\left (x_{\mathfrak {p}}\right )=1$
and
![]() $v_{\mathfrak {p}^{\prime }}\left (x_{\mathfrak {p}}\right )=0$
for any
$v_{\mathfrak {p}^{\prime }}\left (x_{\mathfrak {p}}\right )=0$
for any
![]() $\mathfrak {p}^{\prime }\neq \mathfrak {p}$
satisfying
$\mathfrak {p}^{\prime }\neq \mathfrak {p}$
satisfying
![]() $\mathfrak {p}^{\prime }\mid p$
. We define a map
$\mathfrak {p}^{\prime }\mid p$
. We define a map
 $$ \begin{align*} x_{\mathfrak{p}}^{*}: M\left(\mu_{N}, x_{\mathfrak{p}}^{-1}\mathfrak{c}, \kappa^{\mathcal{U}}\right)\left(\underline{v}\right)\to M\left(\mu_{N}, \mathfrak{c},\kappa^{\mathcal{U}}\right)\left(\underline{v}\right) \end{align*} $$
$$ \begin{align*} x_{\mathfrak{p}}^{*}: M\left(\mu_{N}, x_{\mathfrak{p}}^{-1}\mathfrak{c}, \kappa^{\mathcal{U}}\right)\left(\underline{v}\right)\to M\left(\mu_{N}, \mathfrak{c},\kappa^{\mathcal{U}}\right)\left(\underline{v}\right) \end{align*} $$
by
![]() $f\mapsto \left ((A,\iota ,\lambda ,\psi )\mapsto f\left (A,\iota ,x_{\mathfrak {p}}\lambda ,\psi \right )\right )$
. Then we denote the composite
$f\mapsto \left ((A,\iota ,\lambda ,\psi )\mapsto f\left (A,\iota ,x_{\mathfrak {p}}\lambda ,\psi \right )\right )$
. Then we denote the composite
 $$ \begin{align*} \prod_{\mathfrak{p}\mid p}\left(x_{\mathfrak{p}}^{*}\right)^{v_{\mathfrak{p}}(\mathfrak{l})}\circ T^{\prime}_{\mathfrak{l}}:M\left(\mu_{N}, \prod_{\mathfrak{p}\mid p}x_{\mathfrak{p}}^{-v_{\mathfrak{p}}(\mathfrak{l})}\mathfrak{l}\mathfrak{c}, \kappa^{\mathcal{U}}\right)\left(\underline{v}\right)\to M\left(\mu_{N},\mathfrak{c},\kappa^{\mathcal{U}}\right)\left(\underline{v}\right) \end{align*} $$
$$ \begin{align*} \prod_{\mathfrak{p}\mid p}\left(x_{\mathfrak{p}}^{*}\right)^{v_{\mathfrak{p}}(\mathfrak{l})}\circ T^{\prime}_{\mathfrak{l}}:M\left(\mu_{N}, \prod_{\mathfrak{p}\mid p}x_{\mathfrak{p}}^{-v_{\mathfrak{p}}(\mathfrak{l})}\mathfrak{l}\mathfrak{c}, \kappa^{\mathcal{U}}\right)\left(\underline{v}\right)\to M\left(\mu_{N},\mathfrak{c},\kappa^{\mathcal{U}}\right)\left(\underline{v}\right) \end{align*} $$
by
![]() $T_{\mathfrak {l}}$
. We also write it as
$T_{\mathfrak {l}}$
. We also write it as
![]() $U_{\mathfrak {l}}$
if
$U_{\mathfrak {l}}$
if
![]() $\mathfrak {l}$
divides a power of p. Then the operators
$\mathfrak {l}$
divides a power of p. Then the operators
![]() $T_{\mathfrak {l}}$
for any
$T_{\mathfrak {l}}$
for any
![]() $\mathfrak {l}$
and
$\mathfrak {l}$
and
![]() $S_{\mathfrak {l}}$
for
$S_{\mathfrak {l}}$
for
![]() $(\mathfrak {l}, pN)=1$
define actions on
$(\mathfrak {l}, pN)=1$
define actions on
 $M^{G}\left (\mu _{N},\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )\left (\underline {v}\right )$
and
$M^{G}\left (\mu _{N},\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )\left (\underline {v}\right )$
and
 $S^{G}\left (\mu _{N},\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )\left (\underline {v}\right )$
which commute with each other. Note that
$S^{G}\left (\mu _{N},\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )\left (\underline {v}\right )$
which commute with each other. Note that
![]() $T_{\mathfrak {l}\mathfrak {l}^{\prime }}=T_{\mathfrak {l}} T_{\mathfrak {l}^{\prime }}$
if
$T_{\mathfrak {l}\mathfrak {l}^{\prime }}=T_{\mathfrak {l}} T_{\mathfrak {l}^{\prime }}$
if
![]() $(\mathfrak {l},\mathfrak {l}^{\prime })=1$
and that [Reference Hattori29, Theorem 8.1(10)] implies
$(\mathfrak {l},\mathfrak {l}^{\prime })=1$
and that [Reference Hattori29, Theorem 8.1(10)] implies
 $$ \begin{align} T_{\mathfrak{m}} T_{\mathfrak{m}^{s-1}}= \begin{cases} T_{\mathfrak{m}^{s}}+\mathrm{N}_{F/\mathbb{Q}}(\mathfrak{m})S_{\mathfrak{m}} T_{\mathfrak{m}^{s-2}} & (\mathfrak{m}\nmid Np)\\ T_{\mathfrak{m}^{s}} & (\mathfrak{m} \mid Np) \end{cases} \end{align} $$
$$ \begin{align} T_{\mathfrak{m}} T_{\mathfrak{m}^{s-1}}= \begin{cases} T_{\mathfrak{m}^{s}}+\mathrm{N}_{F/\mathbb{Q}}(\mathfrak{m})S_{\mathfrak{m}} T_{\mathfrak{m}^{s-2}} & (\mathfrak{m}\nmid Np)\\ T_{\mathfrak{m}^{s}} & (\mathfrak{m} \mid Np) \end{cases} \end{align} $$
for any maximal ideal
![]() $\mathfrak {m}$
.
$\mathfrak {m}$
.
Let v be an element of
 $\mathbb {Q}\cap \left (0,\frac {p-1}{p}\right )$
. Note that the foregoing definitions of Hecke operators are also valid for
$\mathbb {Q}\cap \left (0,\frac {p-1}{p}\right )$
. Note that the foregoing definitions of Hecke operators are also valid for
 $S^{G}\left (\mu _{N},\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )(v_{\mathrm {tot}})$
. Then the operator
$S^{G}\left (\mu _{N},\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )(v_{\mathrm {tot}})$
. Then the operator
![]() $U_{p}$
is a compact operator acting on
$U_{p}$
is a compact operator acting on
 $S^{G}\left (\mu _{N},\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )(v_{\mathrm {tot}})$
which factors as
$S^{G}\left (\mu _{N},\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )(v_{\mathrm {tot}})$
which factors as
 $$ \begin{align*} S^{G}\left(\mu_{N},\left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)(v_{\mathrm{tot}})\subseteq S^{G}\left(\mu_{N},\left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)\left(p^{-1}v_{\mathrm{tot}}\right)\to S^{G}\left(\mu_{N},\left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)(v_{\mathrm{tot}}) \end{align*} $$
$$ \begin{align*} S^{G}\left(\mu_{N},\left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)(v_{\mathrm{tot}})\subseteq S^{G}\left(\mu_{N},\left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)\left(p^{-1}v_{\mathrm{tot}}\right)\to S^{G}\left(\mu_{N},\left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)(v_{\mathrm{tot}}) \end{align*} $$
and, for
![]() $v<(p-1)/p^{2}$
, also as
$v<(p-1)/p^{2}$
, also as
 $$ \begin{align*} S^{G}\left(\mu_{N},\left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)(v_{\mathrm{tot}})\to S^{G}\left(\mu_{N},\left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)(p v_{\mathrm{tot}})\subseteq S^{G}\left(\mu_{N},\left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)(v_{\mathrm{tot}}). \end{align*} $$
$$ \begin{align*} S^{G}\left(\mu_{N},\left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)(v_{\mathrm{tot}})\to S^{G}\left(\mu_{N},\left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)(p v_{\mathrm{tot}})\subseteq S^{G}\left(\mu_{N},\left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)(v_{\mathrm{tot}}). \end{align*} $$
Let
![]() $\mathbf {T}$
be the polynomial ring over K with variables
$\mathbf {T}$
be the polynomial ring over K with variables
![]() $T_{\mathfrak {l}}$
for any
$T_{\mathfrak {l}}$
for any
![]() $\mathfrak {l}$
and
$\mathfrak {l}$
and
![]() $S_{\mathfrak {l}}$
for
$S_{\mathfrak {l}}$
for
![]() $(\mathfrak {l}, pN)=1$
. Then the ring
$(\mathfrak {l}, pN)=1$
. Then the ring
![]() $\mathbf {T}$
acts on
$\mathbf {T}$
acts on
 $S^{G}\left (\mu _{N},\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )(v)$
and
$S^{G}\left (\mu _{N},\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )(v)$
and
 $S^{G}\left (\mu _{N},\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )(v_{\mathrm {tot}})$
via the Hecke operators defined.
$S^{G}\left (\mu _{N},\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )(v_{\mathrm {tot}})$
via the Hecke operators defined.
Now we can construct the eigenvariety from these data, as in [Reference Andreatta, Iovita and Pilloni4, §5]. For any positive integer n, we fix a positive rational number
![]() $v_{n}<B_{n}$
satisfying
$v_{n}<B_{n}$
satisfying
![]() $v_{n}\geq v_{n+1}$
for any n, where
$v_{n}\geq v_{n+1}$
for any n, where
![]() $B_{n}$
is defined by equation (3.5). We also assume
$B_{n}$
is defined by equation (3.5). We also assume
![]() $v_{n}\leq \left (p-2+v_{p}(2)\right )/p^{n+1}$
for any
$v_{n}\leq \left (p-2+v_{p}(2)\right )/p^{n+1}$
for any
![]() $n\geq 2$
, so that replacing K with its finite extension, condition (3.7) for
$n\geq 2$
, so that replacing K with its finite extension, condition (3.7) for
![]() $v_{n}$
is satisfied for all n.
$v_{n}$
is satisfied for all n.
For any admissible affinoid open subset
![]() $\mathcal {U}\subseteq \mathcal {W}^{G}$
, we put
$\mathcal {U}\subseteq \mathcal {W}^{G}$
, we put
 $$ \begin{align*} n(\mathcal{U})=\min\left\{n\in \mathbb{Z}_{>0}\mid \left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\text{ is }\textit{n}\text{-analytic}\right\}. \end{align*} $$
$$ \begin{align*} n(\mathcal{U})=\min\left\{n\in \mathbb{Z}_{>0}\mid \left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\text{ is }\textit{n}\text{-analytic}\right\}. \end{align*} $$
We define a Banach
![]() $\mathcal {O}(\mathcal {U})$
-module
$\mathcal {O}(\mathcal {U})$
-module
![]() $M_{\mathcal {U}}$
with
$M_{\mathcal {U}}$
with
![]() $\mathbf {T}$
-action as
$\mathbf {T}$
-action as
 $$ \begin{align*} M_{\mathcal{U}}=S^{G}\left(\mu_{N},\left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)\left(v_{n(\mathcal{U}),\mathrm{tot}}\right), \end{align*} $$
$$ \begin{align*} M_{\mathcal{U}}=S^{G}\left(\mu_{N},\left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)\left(v_{n(\mathcal{U}),\mathrm{tot}}\right), \end{align*} $$
on which
![]() $U_{p}$
acts as a compact operator. The proof of [Reference Andreatta, Iovita and Pilloni4, Theorem 4.4] remains valid also for
$U_{p}$
acts as a compact operator. The proof of [Reference Andreatta, Iovita and Pilloni4, Theorem 4.4] remains valid also for
![]() $p=2$
and implies that the
$p=2$
and implies that the
![]() $\mathcal {O}(\mathcal {U})$
-module
$\mathcal {O}(\mathcal {U})$
-module
![]() $M_{\mathcal {U}}$
satisfies condition
$M_{\mathcal {U}}$
satisfies condition
![]() $(Pr)$
. For admissible affinoid open subsets
$(Pr)$
. For admissible affinoid open subsets
![]() $\mathcal {U}_{1}\subseteq \mathcal {U}_{2}$
of
$\mathcal {U}_{1}\subseteq \mathcal {U}_{2}$
of
![]() $\mathcal {W}^{G}$
, we have
$\mathcal {W}^{G}$
, we have
![]() $n(\mathcal {U}_{1})\leq n(\mathcal {U}_{2})$
and [Reference Andreatta, Iovita and Pilloni4, Proposition 3.14] yields a map
$n(\mathcal {U}_{1})\leq n(\mathcal {U}_{2})$
and [Reference Andreatta, Iovita and Pilloni4, Proposition 3.14] yields a map
 $$ \begin{align*} \alpha_{\mathcal{U}_{1},\mathcal{U}_{2}}: M_{\mathcal{U}_{1}}\to S^{G}\left(\mu_{N},\left(\nu^{\mathcal{U}_{1}},w^{\mathcal{U}_{1}}\right)\right)\left(v_{n\left(\mathcal{U}_{2}\right),\mathrm{tot}}\right)\simeq M_{\mathcal{U}_{2}}\hat{\otimes}_{\mathcal{O}\left(\mathcal{U}_{2}\right)}\mathcal{O}(\mathcal{U}_{1}), \end{align*} $$
$$ \begin{align*} \alpha_{\mathcal{U}_{1},\mathcal{U}_{2}}: M_{\mathcal{U}_{1}}\to S^{G}\left(\mu_{N},\left(\nu^{\mathcal{U}_{1}},w^{\mathcal{U}_{1}}\right)\right)\left(v_{n\left(\mathcal{U}_{2}\right),\mathrm{tot}}\right)\simeq M_{\mathcal{U}_{2}}\hat{\otimes}_{\mathcal{O}\left(\mathcal{U}_{2}\right)}\mathcal{O}(\mathcal{U}_{1}), \end{align*} $$
where the first arrow is the restriction map. Note that for any positive rational numbers
![]() $v,v^{\prime }$
satisfying
$v,v^{\prime }$
satisfying
![]() $v^{\prime }\leq v < pv^{\prime }<(p-1)/p$
, the restriction map
$v^{\prime }\leq v < pv^{\prime }<(p-1)/p$
, the restriction map
 $$ \begin{align*} S^{G}\left(\mu_{N},\left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)(v_{\mathrm{tot}})\to S^{G}\left(\mu_{N},\left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)\left(v^{\prime}_{\mathrm{tot}}\right) \end{align*} $$
$$ \begin{align*} S^{G}\left(\mu_{N},\left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)(v_{\mathrm{tot}})\to S^{G}\left(\mu_{N},\left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)\left(v^{\prime}_{\mathrm{tot}}\right) \end{align*} $$
is a primitive link. Thus the map
![]() $\alpha _{\mathcal {U}_{1},\mathcal {U}_{2}}$
is a link satisfying the cocycle condition. Hence, by applying the eigenvariety machine [Reference Buzzard12, Construction 5.7], we obtain the Hilbert eigenvariety
$\alpha _{\mathcal {U}_{1},\mathcal {U}_{2}}$
is a link satisfying the cocycle condition. Hence, by applying the eigenvariety machine [Reference Buzzard12, Construction 5.7], we obtain the Hilbert eigenvariety
![]() $\mathcal {E}\to \mathcal {W}^{G}$
as in [Reference Andreatta, Iovita and Pilloni4, Theorem 5.1].
$\mathcal {E}\to \mathcal {W}^{G}$
as in [Reference Andreatta, Iovita and Pilloni4, Theorem 5.1].
3.4 The case over
 $\mathbb {C}_{p}$
$\mathbb {C}_{p}$
Since we are ultimately interested in overconvergent Hilbert modular forms over
![]() $\mathbb {C}_{p}$
, we need to give a slight generalization of the construction in [Reference Andreatta, Iovita and Pilloni4] over
$\mathbb {C}_{p}$
, we need to give a slight generalization of the construction in [Reference Andreatta, Iovita and Pilloni4] over
![]() $\mathbb {C}_{p}$
. As before, for any quasi-separated rigid analytic variety
$\mathbb {C}_{p}$
. As before, for any quasi-separated rigid analytic variety
![]() $\mathcal {X}$
over K and any coherent
$\mathcal {X}$
over K and any coherent
![]() $\mathcal {O}_{\mathcal {X}}$
-module
$\mathcal {O}_{\mathcal {X}}$
-module
![]() $\mathcal {F}$
, we denote the base extensions of
$\mathcal {F}$
, we denote the base extensions of
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $\mathcal {F}$
to
$\mathcal {F}$
to
![]() $\mathbb {C}_{p}$
by
$\mathbb {C}_{p}$
by
![]() $\mathcal {X}_{\mathbb {C}_{p}}$
and
$\mathcal {X}_{\mathbb {C}_{p}}$
and
![]() $\mathcal {F}_{\mathbb {C}_{p}}$
, respectively. Similarly, for any quasi-separated admissible formal scheme
$\mathcal {F}_{\mathbb {C}_{p}}$
, respectively. Similarly, for any quasi-separated admissible formal scheme
![]() $\mathfrak {X}$
over
$\mathfrak {X}$
over
![]() $\mathrm {Spf}(\mathcal {O}_{K})$
and any coherent
$\mathrm {Spf}(\mathcal {O}_{K})$
and any coherent
![]() $\mathcal {O}_{\mathfrak {X}}$
-module
$\mathcal {O}_{\mathfrak {X}}$
-module
![]() $\mathfrak {F}$
, we denote their pullbacks to
$\mathfrak {F}$
, we denote their pullbacks to
 $\mathrm {Spf}\left (\mathcal {O}_{\mathbb {C}_{p}}\right )$
by
$\mathrm {Spf}\left (\mathcal {O}_{\mathbb {C}_{p}}\right )$
by
![]() $\mathfrak {X}_{\mathcal {O}_{\mathbb {C}_{p}}}$
and
$\mathfrak {X}_{\mathcal {O}_{\mathbb {C}_{p}}}$
and
![]() $\mathfrak {F}_{\mathcal {O}_{\mathbb {C}_{p}}}$
, respectively. Then on the Raynaud generic fiber we have
$\mathfrak {F}_{\mathcal {O}_{\mathbb {C}_{p}}}$
, respectively. Then on the Raynaud generic fiber we have
 $$ \begin{align*} \left(\mathfrak{X}^{\mathrm{rig}}\right)_{\mathbb{C}_{p}}=\left(\mathfrak{X}_{\mathcal{O}_{\mathbb{C}_{p}}}\right)^{\mathrm{rig}},\qquad \left(\mathfrak{F}^{\mathrm{rig}}\right)_{\mathbb{C}_{p}}=\left(\mathfrak{F}_{\mathcal{O}_{\mathbb{C}_{p}}}\right)^{\mathrm{rig}}. \end{align*} $$
$$ \begin{align*} \left(\mathfrak{X}^{\mathrm{rig}}\right)_{\mathbb{C}_{p}}=\left(\mathfrak{X}_{\mathcal{O}_{\mathbb{C}_{p}}}\right)^{\mathrm{rig}},\qquad \left(\mathfrak{F}^{\mathrm{rig}}\right)_{\mathbb{C}_{p}}=\left(\mathfrak{F}_{\mathcal{O}_{\mathbb{C}_{p}}}\right)^{\mathrm{rig}}. \end{align*} $$
Let
![]() $\mathcal {U}=\mathrm {Sp}(A)$
be a reduced
$\mathcal {U}=\mathrm {Sp}(A)$
be a reduced
![]() $\mathbb {C}_{p}$
-affinoid variety. From [Reference Bosch, Lütkebohmert and Raynaud11, Theorem 1.2] and [Reference Abbes1, Proposition 1.10.2(iii)], we see that
$\mathbb {C}_{p}$
-affinoid variety. From [Reference Bosch, Lütkebohmert and Raynaud11, Theorem 1.2] and [Reference Abbes1, Proposition 1.10.2(iii)], we see that
![]() $A^{\circ }$
is an admissible formal
$A^{\circ }$
is an admissible formal
![]() $\mathcal {O}_{\mathbb {C}_{p}}$
-algebra. Put
$\mathcal {O}_{\mathbb {C}_{p}}$
-algebra. Put
![]() $\mathfrak {U}=\mathrm {Spf}(A^{\circ })$
. For any morphism
$\mathfrak {U}=\mathrm {Spf}(A^{\circ })$
. For any morphism
![]() $\mathcal {U}\to \mathcal {W}_{\mathbb {C}_{p}}$
or
$\mathcal {U}\to \mathcal {W}_{\mathbb {C}_{p}}$
or
 $\mathcal {U}\to \mathcal {W}^{G}_{\mathbb {C}_{p}}$
, we have an associated character
$\mathcal {U}\to \mathcal {W}^{G}_{\mathbb {C}_{p}}$
, we have an associated character
![]() $\kappa ^{\mathcal {U}}$
or
$\kappa ^{\mathcal {U}}$
or
 $\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )$
and a notion of n-analyticity defined in the same way as before. Consider the base extensions
$\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )$
and a notion of n-analyticity defined in the same way as before. Consider the base extensions
 $$ \begin{align*} \pi_{w,\mathcal{O}_{\mathbb{C}_{p}}}: \mathfrak{IW}_{w,\mathcal{O}_{\mathbb{C}_{p}}}^{+} \overset{\gamma_{w,\mathcal{O}_{\mathbb{C}_{p}}}}{\to} \bar{\mathfrak{M}}(\Gamma_{1}(p^{n}),\mu_{N}, \mathfrak{c})\left(\underline{v}\right)_{\mathcal{O}_{\mathbb{C}_{p}}}\overset{h_{n,\mathcal{O}_{\mathbb{C}_{p}}}}{\to} \bar{\mathfrak{M}}(\mu_{N},\mathfrak{c})\left(\underline{v}\right)_{\mathcal{O}_{\mathbb{C}_{p}}} \end{align*} $$
$$ \begin{align*} \pi_{w,\mathcal{O}_{\mathbb{C}_{p}}}: \mathfrak{IW}_{w,\mathcal{O}_{\mathbb{C}_{p}}}^{+} \overset{\gamma_{w,\mathcal{O}_{\mathbb{C}_{p}}}}{\to} \bar{\mathfrak{M}}(\Gamma_{1}(p^{n}),\mu_{N}, \mathfrak{c})\left(\underline{v}\right)_{\mathcal{O}_{\mathbb{C}_{p}}}\overset{h_{n,\mathcal{O}_{\mathbb{C}_{p}}}}{\to} \bar{\mathfrak{M}}(\mu_{N},\mathfrak{c})\left(\underline{v}\right)_{\mathcal{O}_{\mathbb{C}_{p}}} \end{align*} $$
of the maps
![]() $\gamma _{w}$
,
$\gamma _{w}$
,
![]() $h_{n}$
, and
$h_{n}$
, and
![]() $\pi _{w}$
. Then for any n-analytic morphism
$\pi _{w}$
. Then for any n-analytic morphism
![]() $\mathcal {U}\to \mathcal {W}_{\mathbb {C}_{p}}$
, we can define the sheaves
$\mathcal {U}\to \mathcal {W}_{\mathbb {C}_{p}}$
, we can define the sheaves
 $$ \begin{align*} \Omega^{\kappa^{\mathcal{U}}}=\left(\pi^{\mathrm{rig}}_{w,\mathbb{C}_{p}}\right)_{*}\left(\mathcal{O}_{\mathcal{IW}_{w,\mathbb{C}_{p}}^{+}\times \mathcal{U}}\right)\left[-\kappa^{\mathcal{U}}\right],\qquad \mathbf{\Omega}^{\kappa^{\mathcal{U}}}=\left(\pi_{w,\mathcal{O}_{\mathbb{C}_{p}}}\right)_{*}\left(\mathcal{O}_{\mathfrak{IW}_{w,\mathcal{O}_{\mathbb{C}_{p}}}^{+}\times \mathfrak{U}}\right)\left[-\boldsymbol{\kappa}^{\mathcal{U}}\right] \end{align*} $$
$$ \begin{align*} \Omega^{\kappa^{\mathcal{U}}}=\left(\pi^{\mathrm{rig}}_{w,\mathbb{C}_{p}}\right)_{*}\left(\mathcal{O}_{\mathcal{IW}_{w,\mathbb{C}_{p}}^{+}\times \mathcal{U}}\right)\left[-\kappa^{\mathcal{U}}\right],\qquad \mathbf{\Omega}^{\kappa^{\mathcal{U}}}=\left(\pi_{w,\mathcal{O}_{\mathbb{C}_{p}}}\right)_{*}\left(\mathcal{O}_{\mathfrak{IW}_{w,\mathcal{O}_{\mathbb{C}_{p}}}^{+}\times \mathfrak{U}}\right)\left[-\boldsymbol{\kappa}^{\mathcal{U}}\right] \end{align*} $$
such that
 $\Omega ^{\kappa ^{\mathcal {U}}}=\left (\mathbf {\Omega }^{\kappa ^{\mathcal {U}}}\right )^{\mathrm {rig}}$
is an invertible
$\Omega ^{\kappa ^{\mathcal {U}}}=\left (\mathbf {\Omega }^{\kappa ^{\mathcal {U}}}\right )^{\mathrm {rig}}$
is an invertible
 $\mathcal {O}_{\bar {\mathcal {M}}\left (\mu _{N},\mathfrak {c}\right )(v)_{\mathbb {C}_{p}}\times \mathcal {U}}$
-module, as before. [Reference Abbes1, Propositions 1.9.14 and 1.10.2(iii)] implies that
$\mathcal {O}_{\bar {\mathcal {M}}\left (\mu _{N},\mathfrak {c}\right )(v)_{\mathbb {C}_{p}}\times \mathcal {U}}$
-module, as before. [Reference Abbes1, Propositions 1.9.14 and 1.10.2(iii)] implies that
![]() $\mathbf {\Omega }^{\kappa ^{\mathcal {U}}}$
is coherent and that its restriction to
$\mathbf {\Omega }^{\kappa ^{\mathcal {U}}}$
is coherent and that its restriction to
 $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)_{\mathcal {O}_{\mathbb {C}_{p}}}$
is invertible: the latter follows from a similar argument to the proof of [Reference Mumford35, §7, Proposition 2] combined with the fact that
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)_{\mathcal {O}_{\mathbb {C}_{p}}}$
is invertible: the latter follows from a similar argument to the proof of [Reference Mumford35, §7, Proposition 2] combined with the fact that
![]() $h_{n,\mathcal {O}_{\mathbb {C}_{p}}}$
is a
$h_{n,\mathcal {O}_{\mathbb {C}_{p}}}$
is a
![]() $\mathbb {T}(\mathbb {Z}/p^{n}\mathbb {Z})$
-torsor over
$\mathbb {T}(\mathbb {Z}/p^{n}\mathbb {Z})$
-torsor over
 $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)_{\mathcal {O}_{\mathbb {C}_{p}}}$
. Using
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)_{\mathcal {O}_{\mathbb {C}_{p}}}$
. Using
![]() $\Omega ^{\kappa ^{\mathcal {U}}}$
, we define
$\Omega ^{\kappa ^{\mathcal {U}}}$
, we define
 $M\left (\mu _{N},\mathfrak {c},\kappa ^{\mathcal {U}}\right )\left (\underline {v}\right )$
and its variants in the same way as in the case over K.
$M\left (\mu _{N},\mathfrak {c},\kappa ^{\mathcal {U}}\right )\left (\underline {v}\right )$
and its variants in the same way as in the case over K.
For any reduced K-affinoid variety
![]() $\mathcal {V}$
and any n-analytic morphism
$\mathcal {V}$
and any n-analytic morphism
![]() $\mathcal {V}\to \mathcal {W}$
, consider the base extension
$\mathcal {V}\to \mathcal {W}$
, consider the base extension
![]() $\mathcal {V}_{\mathbb {C}_{p}}\to \mathcal {W}_{\mathbb {C}_{p}}$
and the associated character
$\mathcal {V}_{\mathbb {C}_{p}}\to \mathcal {W}_{\mathbb {C}_{p}}$
and the associated character
![]() $\kappa ^{\mathcal {V}_{\mathbb {C}_{p}}}$
. Then we can show that there exist natural isomorphisms
$\kappa ^{\mathcal {V}_{\mathbb {C}_{p}}}$
. Then we can show that there exist natural isomorphisms
 $$ \begin{align} \left(\Omega^{\kappa^{\mathcal{V}}}\right)_{\mathbb{C}_{p}}\simeq \Omega^{\kappa^{\mathcal{V}_{\mathbb{C}_{p}}}},\qquad \Omega^{\kappa^{\mathcal{V}}}(-D)_{\mathbb{C}_{p}}\simeq \Omega^{\kappa^{\mathcal{V}_{\mathbb{C}_{p}}}}(-D) \end{align} $$
$$ \begin{align} \left(\Omega^{\kappa^{\mathcal{V}}}\right)_{\mathbb{C}_{p}}\simeq \Omega^{\kappa^{\mathcal{V}_{\mathbb{C}_{p}}}},\qquad \Omega^{\kappa^{\mathcal{V}}}(-D)_{\mathbb{C}_{p}}\simeq \Omega^{\kappa^{\mathcal{V}_{\mathbb{C}_{p}}}}(-D) \end{align} $$
in the same way as the proof of [Reference Andreatta, Iovita and Pilloni4, Proposition 3.14]. Similarly, for any morphism
![]() $f:\mathcal {U}^{\prime }\to \mathcal {U}$
of reduced
$f:\mathcal {U}^{\prime }\to \mathcal {U}$
of reduced
![]() $\mathbb {C}_{p}$
-affinoid varieties, we have natural isomorphisms
$\mathbb {C}_{p}$
-affinoid varieties, we have natural isomorphisms
 $$ \begin{align} f^{*}\Omega^{\kappa^{\mathcal{U}}}\simeq \Omega^{\kappa^{\mathcal{U}^{\prime}}},\qquad f^{*}\left(\Omega^{\kappa^{\mathcal{U}}}(-D)\right)\simeq \Omega^{\kappa^{\mathcal{U}^{\prime}}}(-D). \end{align} $$
$$ \begin{align} f^{*}\Omega^{\kappa^{\mathcal{U}}}\simeq \Omega^{\kappa^{\mathcal{U}^{\prime}}},\qquad f^{*}\left(\Omega^{\kappa^{\mathcal{U}}}(-D)\right)\simeq \Omega^{\kappa^{\mathcal{U}^{\prime}}}(-D). \end{align} $$
Let
![]() $\bar {M}^{*}(\mu _{N},\mathfrak {c})$
be the minimal compactification of
$\bar {M}^{*}(\mu _{N},\mathfrak {c})$
be the minimal compactification of
![]() $M(\mu _{N},\mathfrak {c})$
. We have a natural proper map
$M(\mu _{N},\mathfrak {c})$
. We have a natural proper map
Note that a sufficiently large power of the usual Hasse invariant can be considered as a global section of an ample invertible sheaf on
![]() $\bar {M}^{*}(\mu _{N},\mathfrak {c})$
. Let
$\bar {M}^{*}(\mu _{N},\mathfrak {c})$
. Let
![]() $\bar {\mathfrak {M}}^{*}(\mu _{N},\mathfrak {c})(v_{\mathrm {tot}})$
be the normal admissible formal scheme defined similarly to
$\bar {\mathfrak {M}}^{*}(\mu _{N},\mathfrak {c})(v_{\mathrm {tot}})$
be the normal admissible formal scheme defined similarly to
![]() $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(v_{\mathrm {tot}})$
using
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(v_{\mathrm {tot}})$
using
![]() $\bar {M}^{*}(\mu _{N},\mathfrak {c})$
instead of
$\bar {M}^{*}(\mu _{N},\mathfrak {c})$
instead of
![]() $\bar {M}(\mu _{N},\mathfrak {c})$
. Let
$\bar {M}(\mu _{N},\mathfrak {c})$
. Let
![]() $\bar {\mathcal {M}}^{*}(\mu _{N},\mathfrak {c})(v_{\mathrm {tot}})$
be its Raynaud generic fiber. By the foregoing ampleness property, we see that
$\bar {\mathcal {M}}^{*}(\mu _{N},\mathfrak {c})(v_{\mathrm {tot}})$
be its Raynaud generic fiber. By the foregoing ampleness property, we see that
![]() $\bar {\mathcal {M}}^{*}(\mu _{N},\mathfrak {c})(v_{\mathrm {tot}})$
is a K-affinoid variety. We also have proper morphisms
$\bar {\mathcal {M}}^{*}(\mu _{N},\mathfrak {c})(v_{\mathrm {tot}})$
is a K-affinoid variety. We also have proper morphisms
 $$ \begin{align*} \rho &: \bar{\mathfrak{M}}(\Gamma_{1}(p^{n}),\mu_{N},\mathfrak{c})(v_{\mathrm{tot}}) \to \bar{\mathfrak{M}}^{*}(\mu_{N},\mathfrak{c})(v_{\mathrm{tot}}),\\ \rho^{\mathrm{rig}} &: \bar{\mathcal{M}}(\Gamma_{1}(p^{n}),\mu_{N},\mathfrak{c})(v_{\mathrm{tot}})\to \bar{\mathcal{M}}^{*}(\mu_{N},\mathfrak{c})(v_{\mathrm{tot}}). \end{align*} $$
$$ \begin{align*} \rho &: \bar{\mathfrak{M}}(\Gamma_{1}(p^{n}),\mu_{N},\mathfrak{c})(v_{\mathrm{tot}}) \to \bar{\mathfrak{M}}^{*}(\mu_{N},\mathfrak{c})(v_{\mathrm{tot}}),\\ \rho^{\mathrm{rig}} &: \bar{\mathcal{M}}(\Gamma_{1}(p^{n}),\mu_{N},\mathfrak{c})(v_{\mathrm{tot}})\to \bar{\mathcal{M}}^{*}(\mu_{N},\mathfrak{c})(v_{\mathrm{tot}}). \end{align*} $$
By the base extension, these induce proper morphisms
 $$ \begin{align*} \rho_{\mathcal{O}_{\mathbb{C}_{p}}} &: \bar{\mathfrak{M}}(\Gamma_{1}(p^{n}),\mu_{N},\mathfrak{c})(v_{\mathrm{tot}})_{\mathcal{O}_{\mathbb{C}_{p}}} \to \bar{\mathfrak{M}}^{*}(\mu_{N},\mathfrak{c})(v_{\mathrm{tot}})_{\mathcal{O}_{\mathbb{C}_{p}}},\\ \rho^{\mathrm{rig}}_{\mathbb{C}_{p}} &: \bar{\mathcal{M}}(\Gamma_{1}(p^{n}),\mu_{N},\mathfrak{c})(v_{\mathrm{tot}})_{\mathbb{C}_{p}}\to \bar{\mathcal{M}}^{*}(\mu_{N},\mathfrak{c})(v_{\mathrm{tot}})_{\mathbb{C}_{p}}. \end{align*} $$
$$ \begin{align*} \rho_{\mathcal{O}_{\mathbb{C}_{p}}} &: \bar{\mathfrak{M}}(\Gamma_{1}(p^{n}),\mu_{N},\mathfrak{c})(v_{\mathrm{tot}})_{\mathcal{O}_{\mathbb{C}_{p}}} \to \bar{\mathfrak{M}}^{*}(\mu_{N},\mathfrak{c})(v_{\mathrm{tot}})_{\mathcal{O}_{\mathbb{C}_{p}}},\\ \rho^{\mathrm{rig}}_{\mathbb{C}_{p}} &: \bar{\mathcal{M}}(\Gamma_{1}(p^{n}),\mu_{N},\mathfrak{c})(v_{\mathrm{tot}})_{\mathbb{C}_{p}}\to \bar{\mathcal{M}}^{*}(\mu_{N},\mathfrak{c})(v_{\mathrm{tot}})_{\mathbb{C}_{p}}. \end{align*} $$
Lemma 3.11. Let
![]() $\mathcal {V}$
be a reduced K-affinoid variety and let
$\mathcal {V}$
be a reduced K-affinoid variety and let
![]() $\mathcal {V}\to \mathcal {W}^{G}$
be an n-analytic morphism. Then the natural base change map
$\mathcal {V}\to \mathcal {W}^{G}$
be an n-analytic morphism. Then the natural base change map
 $$ \begin{align*} (\rho\times 1)_{*} \left(\mathbf{\Omega}^{\kappa^{\mathcal{V}}}(-D)\right)_{\mathcal{O}_{\mathbb{C}_{p}}}\to \left(\rho_{\mathcal{O}_{\mathbb{C}_{p}}}\times 1\right)_{*}\left(\mathbf{\Omega}^{\kappa^{\mathcal{V}}}(-D)_{\mathcal{O}_{\mathbb{C}_{p}}}\right) \end{align*} $$
$$ \begin{align*} (\rho\times 1)_{*} \left(\mathbf{\Omega}^{\kappa^{\mathcal{V}}}(-D)\right)_{\mathcal{O}_{\mathbb{C}_{p}}}\to \left(\rho_{\mathcal{O}_{\mathbb{C}_{p}}}\times 1\right)_{*}\left(\mathbf{\Omega}^{\kappa^{\mathcal{V}}}(-D)_{\mathcal{O}_{\mathbb{C}_{p}}}\right) \end{align*} $$
is an isomorphism. Moreover, we have
 $$ \begin{align*} R^{q} \left(\rho_{\mathcal{O}_{\mathbb{C}_{p}}}\times 1\right)_{*}\left(\mathbf{\Omega}^{\kappa^{\mathcal{V}}}(-D)_{\mathcal{O}_{\mathbb{C}_{p}}}\right)=0 \end{align*} $$
$$ \begin{align*} R^{q} \left(\rho_{\mathcal{O}_{\mathbb{C}_{p}}}\times 1\right)_{*}\left(\mathbf{\Omega}^{\kappa^{\mathcal{V}}}(-D)_{\mathcal{O}_{\mathbb{C}_{p}}}\right)=0 \end{align*} $$
for any
![]() $q>0$
.
$q>0$
.
Proof. It is enough to show the claim formal-locally. Put
![]() $\mathcal {V}=\mathrm {Sp}(A)$
and
$\mathcal {V}=\mathrm {Sp}(A)$
and
![]() $\mathfrak {V}=\mathrm {Spf}(A^{\circ })$
. Let
$\mathfrak {V}=\mathrm {Spf}(A^{\circ })$
. Let
![]() $\mathfrak {Y}$
be a formal affine open subscheme of
$\mathfrak {Y}$
be a formal affine open subscheme of
![]() $\bar {\mathfrak {M}}^{*}(\mu _{N},\mathfrak {c})(v_{\mathrm {tot}})$
and put
$\bar {\mathfrak {M}}^{*}(\mu _{N},\mathfrak {c})(v_{\mathrm {tot}})$
and put
![]() $\mathfrak {X}=\rho ^{-1}(\mathfrak {Y})$
. Since
$\mathfrak {X}=\rho ^{-1}(\mathfrak {Y})$
. Since
![]() $\rho $
is proper of finite presentation and
$\rho $
is proper of finite presentation and
 $\mathbf {\Omega }^{\kappa ^{\mathcal {V}}}(-D)$
is coherent, [Reference Abbes1, (2.11.8.1)] implies that the restriction
$\mathbf {\Omega }^{\kappa ^{\mathcal {V}}}(-D)$
is coherent, [Reference Abbes1, (2.11.8.1)] implies that the restriction
 $$ \begin{align*} R^{q}(\rho\times 1)_{*} \left(\mathbf{\Omega}^{\kappa^{\mathcal{V}}}(-D)\right)\rvert_{\mathfrak{Y}\times\mathfrak{V}} \end{align*} $$
$$ \begin{align*} R^{q}(\rho\times 1)_{*} \left(\mathbf{\Omega}^{\kappa^{\mathcal{V}}}(-D)\right)\rvert_{\mathfrak{Y}\times\mathfrak{V}} \end{align*} $$
is the coherent sheaf associated to the
![]() $\mathcal {O}(\mathfrak {Y}\times \mathfrak {V})$
-module
$\mathcal {O}(\mathfrak {Y}\times \mathfrak {V})$
-module
 $$ \begin{align*} H^{q}\left(\mathfrak{X}\times \mathfrak{V},\mathbf{\Omega}^{\kappa^{\mathcal{V}}}(-D)\right). \end{align*} $$
$$ \begin{align*} H^{q}\left(\mathfrak{X}\times \mathfrak{V},\mathbf{\Omega}^{\kappa^{\mathcal{V}}}(-D)\right). \end{align*} $$
By [Reference Andreatta, Iovita and Pilloni4, Corollary 3.20], we have
 $H^{q}\left (\mathfrak {X}\times \mathfrak {V},\mathbf {\Omega }^{\kappa ^{\mathcal {V}}}(-D)\right )=0$
for any
$H^{q}\left (\mathfrak {X}\times \mathfrak {V},\mathbf {\Omega }^{\kappa ^{\mathcal {V}}}(-D)\right )=0$
for any
![]() $q>0$
.
$q>0$
.
Since
![]() $\mathfrak {X}$
is quasi-compact, we can take a finite covering
$\mathfrak {X}$
is quasi-compact, we can take a finite covering
![]() $\mathfrak {X}=\bigcup _{i=1}^{r} \mathfrak {X}_{i}$
by formal affine open subschemes
$\mathfrak {X}=\bigcup _{i=1}^{r} \mathfrak {X}_{i}$
by formal affine open subschemes
![]() $\mathfrak {X}_{i}$
. Consider the Čech complex for the coherent sheaf
$\mathfrak {X}_{i}$
. Consider the Čech complex for the coherent sheaf
 $\mathbf {\Omega }^{\kappa ^{\mathcal {V}}}(-D)$
$\mathbf {\Omega }^{\kappa ^{\mathcal {V}}}(-D)$
 $$ \begin{align*} 0 \to H^{0}\left(\mathfrak{X}\times \mathfrak{V}, \mathbf{\Omega}^{\kappa^{\mathcal{V}}}(-D)\right)\to C^{0}\left(\mathbf{\Omega}^{\kappa^{\mathcal{V}}}(-D)\right)\to C^{1}\left(\mathbf{\Omega}^{\kappa^{\mathcal{V}}}(-D)\right)\to\dotsb \end{align*} $$
$$ \begin{align*} 0 \to H^{0}\left(\mathfrak{X}\times \mathfrak{V}, \mathbf{\Omega}^{\kappa^{\mathcal{V}}}(-D)\right)\to C^{0}\left(\mathbf{\Omega}^{\kappa^{\mathcal{V}}}(-D)\right)\to C^{1}\left(\mathbf{\Omega}^{\kappa^{\mathcal{V}}}(-D)\right)\to\dotsb \end{align*} $$
with respect to the covering
![]() $\mathfrak {X}\times \mathfrak {V} =\bigcup _{i=1}^{r} \mathfrak {X}_{i}\times \mathfrak {V}$
, which is exact by the foregoing vanishing. From the definition, we see that the sheaf
$\mathfrak {X}\times \mathfrak {V} =\bigcup _{i=1}^{r} \mathfrak {X}_{i}\times \mathfrak {V}$
, which is exact by the foregoing vanishing. From the definition, we see that the sheaf
 $\mathbf {\Omega }^{\kappa ^{\mathcal {V}}}(-D)$
is flat over
$\mathbf {\Omega }^{\kappa ^{\mathcal {V}}}(-D)$
is flat over
![]() $\mathcal {O}_{K}$
and each
$\mathcal {O}_{K}$
and each
![]() $\mathcal {O}_{K}$
-module
$\mathcal {O}_{K}$
-module
 $C^{q}\left (\mathbf {\Omega }^{\kappa ^{\mathcal {V}}}(-D)\right )$
is also flat. By taking modulo
$C^{q}\left (\mathbf {\Omega }^{\kappa ^{\mathcal {V}}}(-D)\right )$
is also flat. By taking modulo
![]() $p^{n}$
, tensoring
$p^{n}$
, tensoring
![]() $\mathcal {O}_{\mathbb {C}_{p}}$
, and taking the inverse limit, we see that the sequence is exact even after taking
$\mathcal {O}_{\mathbb {C}_{p}}$
, and taking the inverse limit, we see that the sequence is exact even after taking
 $-\hat {\otimes }_{\mathcal {O}_{K}}\mathcal {O}_{\mathbb {C}_{p}}$
. This means that the Čech complex for the coherent sheaf
$-\hat {\otimes }_{\mathcal {O}_{K}}\mathcal {O}_{\mathbb {C}_{p}}$
. This means that the Čech complex for the coherent sheaf
 $\mathbf {\Omega }^{\kappa ^{\mathcal {V}}}(-D)_{\mathcal {O}_{\mathbb {C}_{p}}}$
with respect to the formal open covering
$\mathbf {\Omega }^{\kappa ^{\mathcal {V}}}(-D)_{\mathcal {O}_{\mathbb {C}_{p}}}$
with respect to the formal open covering
 $\mathfrak {X}_{\mathcal {O}_{\mathbb {C}_{p}}}\times \mathfrak {V}_{\mathcal {O}_{\mathbb {C}_{p}}}=\bigcup _{i=1}^{r} \mathfrak {X}_{i,\mathcal {O}_{\mathbb {C}_{p}}}\times \mathfrak {V}_{\mathcal {O}_{\mathbb {C}_{p}}}$
is exact except the zeroth degree. Taking the zeroth cohomology gives an isomorphism
$\mathfrak {X}_{\mathcal {O}_{\mathbb {C}_{p}}}\times \mathfrak {V}_{\mathcal {O}_{\mathbb {C}_{p}}}=\bigcup _{i=1}^{r} \mathfrak {X}_{i,\mathcal {O}_{\mathbb {C}_{p}}}\times \mathfrak {V}_{\mathcal {O}_{\mathbb {C}_{p}}}$
is exact except the zeroth degree. Taking the zeroth cohomology gives an isomorphism
 $$ \begin{align*} H^{0}\left(\mathfrak{X}\times \mathfrak{V}, \mathbf{\Omega}^{\kappa^{\mathcal{V}}}(-D)\right)\hat{\otimes}_{\mathcal{O}_{K}}\mathcal{O}_{\mathbb{C}_{p}}\to H^{0}\left(\mathfrak{X}_{\mathcal{O}_{\mathbb{C}_{p}}}\times \mathfrak{V}_{\mathcal{O}_{\mathbb{C}_{p}}}, \mathbf{\Omega}^{\kappa^{\mathcal{V}}}(-D)_{\mathcal{O}_{\mathbb{C}_{p}}}\right) \end{align*} $$
$$ \begin{align*} H^{0}\left(\mathfrak{X}\times \mathfrak{V}, \mathbf{\Omega}^{\kappa^{\mathcal{V}}}(-D)\right)\hat{\otimes}_{\mathcal{O}_{K}}\mathcal{O}_{\mathbb{C}_{p}}\to H^{0}\left(\mathfrak{X}_{\mathcal{O}_{\mathbb{C}_{p}}}\times \mathfrak{V}_{\mathcal{O}_{\mathbb{C}_{p}}}, \mathbf{\Omega}^{\kappa^{\mathcal{V}}}(-D)_{\mathcal{O}_{\mathbb{C}_{p}}}\right) \end{align*} $$
and the qth cohomology for
![]() $q>0$
gives
$q>0$
gives
 $$ \begin{align*} H^{q}\left(\mathfrak{X}_{\mathcal{O}_{\mathbb{C}_{p}}}\times \mathfrak{V}_{\mathcal{O}_{\mathbb{C}_{p}}}, \mathbf{\Omega}^{\kappa^{\mathcal{V}}}(-D)_{\mathcal{O}_{\mathbb{C}_{p}}}\right)=0. \end{align*} $$
$$ \begin{align*} H^{q}\left(\mathfrak{X}_{\mathcal{O}_{\mathbb{C}_{p}}}\times \mathfrak{V}_{\mathcal{O}_{\mathbb{C}_{p}}}, \mathbf{\Omega}^{\kappa^{\mathcal{V}}}(-D)_{\mathcal{O}_{\mathbb{C}_{p}}}\right)=0. \end{align*} $$
This concludes the proof.
Lemma 3.12. Let
![]() $\mathcal {V}$
be a reduced K-affinoid variety and let
$\mathcal {V}$
be a reduced K-affinoid variety and let
![]() $\mathcal {V}\to \mathcal {W}^{G}$
be an n-analytic morphism. Then the natural map
$\mathcal {V}\to \mathcal {W}^{G}$
be an n-analytic morphism. Then the natural map
 $$ \begin{align*} S^{G}\left(\mu_{N},\left(\nu^{\mathcal{V}},w^{\mathcal{V}}\right)\right)(v_{\mathrm{tot}})\hat{\otimes}_{K} \mathbb{C}_{p} \to S^{G}\left(\mu_{N},\left(\nu^{\mathcal{V}_{\mathbb{C}_{p}}},w^{\mathcal{V}_{\mathbb{C}_{p}}}\right)\right)(v_{\mathrm{tot}}) \end{align*} $$
$$ \begin{align*} S^{G}\left(\mu_{N},\left(\nu^{\mathcal{V}},w^{\mathcal{V}}\right)\right)(v_{\mathrm{tot}})\hat{\otimes}_{K} \mathbb{C}_{p} \to S^{G}\left(\mu_{N},\left(\nu^{\mathcal{V}_{\mathbb{C}_{p}}},w^{\mathcal{V}_{\mathbb{C}_{p}}}\right)\right)(v_{\mathrm{tot}}) \end{align*} $$
is an isomorphism.
Proof. Put
![]() $\mathcal {V}=\mathrm {Sp}(A)$
. By taking the Raynaud generic fibers and [Reference Abbes1, Propositions 4.7.23 and 4.7.36], we see from Lemma 3.11 that the base-change map
$\mathcal {V}=\mathrm {Sp}(A)$
. By taking the Raynaud generic fibers and [Reference Abbes1, Propositions 4.7.23 and 4.7.36], we see from Lemma 3.11 that the base-change map
 $$ \begin{align*} \left(\rho^{\mathrm{rig}} \times 1\right)_{*} \left(\Omega^{\kappa^{\mathcal{V}}}(-D)\right)_{\mathbb{C}_{p}}\to \left(\rho_{\mathbb{C}_{p}}\times 1\right)_{*}\left(\Omega^{\kappa^{\mathcal{V}}}(-D)_{\mathbb{C}_{p}}\right) \end{align*} $$
$$ \begin{align*} \left(\rho^{\mathrm{rig}} \times 1\right)_{*} \left(\Omega^{\kappa^{\mathcal{V}}}(-D)\right)_{\mathbb{C}_{p}}\to \left(\rho_{\mathbb{C}_{p}}\times 1\right)_{*}\left(\Omega^{\kappa^{\mathcal{V}}}(-D)_{\mathbb{C}_{p}}\right) \end{align*} $$
is an isomorphism. By formula (3.9), the latter sheaf is isomorphic to the sheaf
 $\left (\rho _{\mathbb {C}_{p}}\times 1\right )_{*}\left (\Omega ^{\kappa ^{\mathcal {V}_{\mathbb {C}_{p}}}}(-D)\right )$
. Since
$\left (\rho _{\mathbb {C}_{p}}\times 1\right )_{*}\left (\Omega ^{\kappa ^{\mathcal {V}_{\mathbb {C}_{p}}}}(-D)\right )$
. Since
![]() $\bar {\mathcal {M}}^{*}(\mu _{N},\mathfrak {c})(v_{\mathrm {tot}})_{\mathbb {C}_{p}}\times \mathcal {V}_{\mathbb {C}_{p}}$
is a
$\bar {\mathcal {M}}^{*}(\mu _{N},\mathfrak {c})(v_{\mathrm {tot}})_{\mathbb {C}_{p}}\times \mathcal {V}_{\mathbb {C}_{p}}$
is a
![]() $\mathbb {C}_{p}$
-affinoid variety, taking global sections yields an isomorphism
$\mathbb {C}_{p}$
-affinoid variety, taking global sections yields an isomorphism
 $$ \begin{align} &H^{0}\left(\bar{\mathcal{M}}(\Gamma_{1}(p^{n}), \mu_{N},\mathfrak{c})(v_{\mathrm{tot}})\times \mathcal{V},\Omega^{\kappa^{\mathcal{V}}}(-D)\right)\hat{\otimes}_{K}\mathbb{C}_{p}\to \nonumber\\ &\qquad\qquad\qquad\qquad\qquad\qquad H^{0}\left(\bar{\mathcal{M}}(\Gamma_{1}(p^{n}), \mu_{N},\mathfrak{c})(v_{\mathrm{tot}})_{\mathbb{C}_{p}}\times \mathcal{V}_{\mathbb{C}_{p}},\Omega^{\kappa^{\mathcal{V}_{\mathbb{C}_{p}}}}(-D)\right). \end{align} $$
$$ \begin{align} &H^{0}\left(\bar{\mathcal{M}}(\Gamma_{1}(p^{n}), \mu_{N},\mathfrak{c})(v_{\mathrm{tot}})\times \mathcal{V},\Omega^{\kappa^{\mathcal{V}}}(-D)\right)\hat{\otimes}_{K}\mathbb{C}_{p}\to \nonumber\\ &\qquad\qquad\qquad\qquad\qquad\qquad H^{0}\left(\bar{\mathcal{M}}(\Gamma_{1}(p^{n}), \mu_{N},\mathfrak{c})(v_{\mathrm{tot}})_{\mathbb{C}_{p}}\times \mathcal{V}_{\mathbb{C}_{p}},\Omega^{\kappa^{\mathcal{V}_{\mathbb{C}_{p}}}}(-D)\right). \end{align} $$
Taking the
![]() $\mathbb {T}(\mathbb {Z}/p^{n}\mathbb {Z})$
-equivariant part and the
$\mathbb {T}(\mathbb {Z}/p^{n}\mathbb {Z})$
-equivariant part and the
![]() $\Delta $
-fixed part, we obtain the lemma.
$\Delta $
-fixed part, we obtain the lemma.
Lemma 3.13. Let
![]() $\mathcal {V}=\mathrm {Sp}(A)$
be a reduced K-affinoid variety and let
$\mathcal {V}=\mathrm {Sp}(A)$
be a reduced K-affinoid variety and let
![]() $\mathcal {V}\to \mathcal {W}^{G}$
be an n-analytic morphism. Let x be an element of
$\mathcal {V}\to \mathcal {W}^{G}$
be an n-analytic morphism. Let x be an element of
![]() $\mathcal {V}(\mathbb {C}_{p})$
and let
$\mathcal {V}(\mathbb {C}_{p})$
and let
![]() $x^{*}:A \to \mathbb {C}_{p}$
be the ring homomorphism defined by x. Suppose that the maximal ideal
$x^{*}:A \to \mathbb {C}_{p}$
be the ring homomorphism defined by x. Suppose that the maximal ideal
![]() $m_{x}$
of
$m_{x}$
of
 $A_{\mathbb {C}_{p}}=A\hat {\otimes }_{K} \mathbb {C}_{p}$
corresponding to x is generated by a regular sequence. Put
$A_{\mathbb {C}_{p}}=A\hat {\otimes }_{K} \mathbb {C}_{p}$
corresponding to x is generated by a regular sequence. Put
 $(\nu ,w)=\left (\nu ^{\mathcal {V}}(x),w^{\mathcal {V}}(x)\right )$
. Then the specialization map
$(\nu ,w)=\left (\nu ^{\mathcal {V}}(x),w^{\mathcal {V}}(x)\right )$
. Then the specialization map
 $$ \begin{align*} S^{G}\left(\mu_{N}, \left(\nu^{\mathcal{V}},w^{\mathcal{V}}\right)\right)(v_{\mathrm{tot}})\hat{\otimes}_{A,x^{*}}\mathbb{C}_{p}\to S^{G}(\mu_{N}, (\nu,w))(v_{\mathrm{tot}}) \end{align*} $$
$$ \begin{align*} S^{G}\left(\mu_{N}, \left(\nu^{\mathcal{V}},w^{\mathcal{V}}\right)\right)(v_{\mathrm{tot}})\hat{\otimes}_{A,x^{*}}\mathbb{C}_{p}\to S^{G}(\mu_{N}, (\nu,w))(v_{\mathrm{tot}}) \end{align*} $$
is an isomorphism.
Proof. This is essentially proved in [Reference Andreatta, Iovita and Pilloni4, Proposition 3.23]. Put
 $\kappa ^{\mathcal {V}}=k\left (\nu ^{\mathcal {V}},w^{\mathcal {V}}\right )$
and
$\kappa ^{\mathcal {V}}=k\left (\nu ^{\mathcal {V}},w^{\mathcal {V}}\right )$
and
![]() $\kappa =k(\nu ,w)$
. By the assumption on
$\kappa =k(\nu ,w)$
. By the assumption on
![]() $m_{x}$
, we have the Koszul resolution
$m_{x}$
, we have the Koszul resolution
 $$ \begin{align*} 0\to A_{\mathbb{C}_{p}} \to A^{n_{r}}_{\mathbb{C}_{p}} \to \dotsb \to A^{n_{1}}_{\mathbb{C}_{p}}\to A_{\mathbb{C}_{p}} \to A_{\mathbb{C}_{p}}/m_{x} \to 0 \end{align*} $$
$$ \begin{align*} 0\to A_{\mathbb{C}_{p}} \to A^{n_{r}}_{\mathbb{C}_{p}} \to \dotsb \to A^{n_{1}}_{\mathbb{C}_{p}}\to A_{\mathbb{C}_{p}} \to A_{\mathbb{C}_{p}}/m_{x} \to 0 \end{align*} $$
with some nonnegative integers
![]() $n_{1},\dotsc ,n_{r}$
, which induces a finite resolution of the sheaf
$n_{1},\dotsc ,n_{r}$
, which induces a finite resolution of the sheaf
![]() $(1\times x)_{*}(\Omega ^{\kappa }(-D))$
by finite direct sums of
$(1\times x)_{*}(\Omega ^{\kappa }(-D))$
by finite direct sums of
 $\Omega ^{\kappa ^{\mathcal {V}}}(-D)_{\mathbb {C}_{p}}$
. By Lemma 3.11, the push-forward of this resolution by the map
$\Omega ^{\kappa ^{\mathcal {V}}}(-D)_{\mathbb {C}_{p}}$
. By Lemma 3.11, the push-forward of this resolution by the map
 $\rho ^{\mathrm {rig}}_{\mathbb {C}_{p}}\times 1$
is exact. Since
$\rho ^{\mathrm {rig}}_{\mathbb {C}_{p}}\times 1$
is exact. Since
![]() $\bar {\mathcal {M}}^{*}(\mu _{N},\mathfrak {c})(v_{\mathrm {tot}})_{\mathbb {C}_{p}}\times \mathcal {V}_{\mathbb {C}_{p}}$
is a
$\bar {\mathcal {M}}^{*}(\mu _{N},\mathfrak {c})(v_{\mathrm {tot}})_{\mathbb {C}_{p}}\times \mathcal {V}_{\mathbb {C}_{p}}$
is a
![]() $\mathbb {C}_{p}$
-affinoid variety, the sequence obtained by taking global sections is also exact. This and formula (3.11) yield isomorphisms
$\mathbb {C}_{p}$
-affinoid variety, the sequence obtained by taking global sections is also exact. This and formula (3.11) yield isomorphisms
 $$ \begin{align*} H^{0}\left(\bar{\mathcal{M}}\vphantom{\Omega^{\kappa^{\mathcal{V}}}}\right.&\left.(\Gamma_{1}(p^{n}),\mu_{N},\mathfrak{c}\vphantom{\Omega^{\kappa^{\mathcal{V}}}})(v_{\mathrm{tot}})\times \mathcal{V}, \Omega^{\kappa^{\mathcal{V}}}(-D)\right)\hat{\otimes}_{A,x^{*}}\mathbb{C}_{p}\\ &\simeq H^{0}\left(\bar{\mathcal{M}}(\Gamma_{1}(p^{n}),\mu_{N},\mathfrak{c})(v_{\mathrm{tot}})_{\mathbb{C}_{p}}\times \mathcal{V}_{\mathbb{C}_{p}}, \Omega^{\kappa^{\mathcal{V}_{\mathbb{C}_{p}}}}(-D)\right)\hat{\otimes}_{A_{\mathbb{C}_{p}},x^{*}}\mathbb{C}_{p}\\ &\simeq H^{0}\left(\bar{\mathcal{M}}(\Gamma_{1}(p^{n}),\mu_{N},\mathfrak{c})(v_{\mathrm{tot}})_{\mathbb{C}_{p}}, \Omega^{\kappa}(-D)\right). \end{align*} $$
$$ \begin{align*} H^{0}\left(\bar{\mathcal{M}}\vphantom{\Omega^{\kappa^{\mathcal{V}}}}\right.&\left.(\Gamma_{1}(p^{n}),\mu_{N},\mathfrak{c}\vphantom{\Omega^{\kappa^{\mathcal{V}}}})(v_{\mathrm{tot}})\times \mathcal{V}, \Omega^{\kappa^{\mathcal{V}}}(-D)\right)\hat{\otimes}_{A,x^{*}}\mathbb{C}_{p}\\ &\simeq H^{0}\left(\bar{\mathcal{M}}(\Gamma_{1}(p^{n}),\mu_{N},\mathfrak{c})(v_{\mathrm{tot}})_{\mathbb{C}_{p}}\times \mathcal{V}_{\mathbb{C}_{p}}, \Omega^{\kappa^{\mathcal{V}_{\mathbb{C}_{p}}}}(-D)\right)\hat{\otimes}_{A_{\mathbb{C}_{p}},x^{*}}\mathbb{C}_{p}\\ &\simeq H^{0}\left(\bar{\mathcal{M}}(\Gamma_{1}(p^{n}),\mu_{N},\mathfrak{c})(v_{\mathrm{tot}})_{\mathbb{C}_{p}}, \Omega^{\kappa}(-D)\right). \end{align*} $$
Taking the
![]() $\mathbb {T}(\mathbb {Z}/p^{n}\mathbb {Z})$
-equivariant part and the
$\mathbb {T}(\mathbb {Z}/p^{n}\mathbb {Z})$
-equivariant part and the
![]() $\Delta $
-fixed part shows the lemma.
$\Delta $
-fixed part shows the lemma.
We can naturally extend the Hecke operators over
![]() $\mathbb {C}_{p}$
: Let
$\mathbb {C}_{p}$
: Let
![]() $\mathcal {U}$
be a smooth
$\mathcal {U}$
be a smooth
![]() $\mathbb {C}_{p}$
-affinoid variety and let
$\mathbb {C}_{p}$
-affinoid variety and let
 $\mathcal {U}\to \mathcal {W}^{G}_{\mathbb {C}_{p}}$
be an n-analytic morphism. Consider the base extension of the isomorphism
$\mathcal {U}\to \mathcal {W}^{G}_{\mathbb {C}_{p}}$
be an n-analytic morphism. Consider the base extension of the isomorphism
![]() $\pi _{\mathfrak {l}}$
$\pi _{\mathfrak {l}}$
 $$ \begin{align*} \pi_{\mathfrak{l}, \mathbb{C}_{p}}: p_{2}^{*} \mathcal{IW}_{w,\mathfrak{l}\mathfrak{c}}^{+}(v)_{\mathbb{C}_{p}} \simeq p_{1}^{*}\mathcal{IW}_{w,\mathfrak{c}}^{+}(v)_{\mathbb{C}_{p}}, \end{align*} $$
$$ \begin{align*} \pi_{\mathfrak{l}, \mathbb{C}_{p}}: p_{2}^{*} \mathcal{IW}_{w,\mathfrak{l}\mathfrak{c}}^{+}(v)_{\mathbb{C}_{p}} \simeq p_{1}^{*}\mathcal{IW}_{w,\mathfrak{c}}^{+}(v)_{\mathbb{C}_{p}}, \end{align*} $$
which defines an isomorphism
 $$ \begin{align*} \pi_{\mathfrak{l},\mathbb{C}_{p}}^{*}: p_{1}^{*}\left(\Omega^{\kappa^{\mathcal{U}}}\right)\simeq p_{2}^{*}\left(\Omega^{\kappa^{\mathcal{U}}}\right). \end{align*} $$
$$ \begin{align*} \pi_{\mathfrak{l},\mathbb{C}_{p}}^{*}: p_{1}^{*}\left(\Omega^{\kappa^{\mathcal{U}}}\right)\simeq p_{2}^{*}\left(\Omega^{\kappa^{\mathcal{U}}}\right). \end{align*} $$
We define the Hecke operator
![]() $T_{\mathfrak {l}}$
over
$T_{\mathfrak {l}}$
over
![]() $\mathbb {C}_{p}$
for
$\mathbb {C}_{p}$
for
![]() $(\mathfrak {l},p)=1$
by
$(\mathfrak {l},p)=1$
by
 $$ \begin{align*} H^{0}\left(\mathcal{M}(\mu_{N},\mathfrak{l}\mathfrak{c})\left(\underline{v}\right)_{\mathbb{C}_{p}}\times \mathcal{U},\Omega^{\kappa^{\mathcal{U}}}\right)& \overset{p_{2}^{*}}{\to} H^{0}\left(\mathcal{Y}^{\prime}_{\mathfrak{c},\mathfrak{l}}\left(\underline{v}\right)_{\mathbb{C}_{p}}\times \mathcal{U},p_{2}^{*}\Omega^{\kappa^{\mathcal{U}}}\right)\\ & \overset{\left(\pi_{\mathfrak{l},\mathbb{C}_{p}}^{*}\right)^{-1}}{\to} H^{0}\left(\mathcal{Y}^{\prime}_{\mathfrak{c},\mathfrak{l}}\left(\underline{v}\right)_{\mathbb{C}_{p}}\times \mathcal{U},p_{1}^{*}\Omega^{\kappa^{\mathcal{U}}}\right)\\ & \overset{\mathrm{N}_{F/\mathbb{Q}}(\mathfrak{l})^{-1}\mathrm{Tr}_{p_{1}}}{\to} H^{0}\left(\mathcal{M}(\mu_{N},\mathfrak{c})(\underline{v})_{\mathbb{C}_{p}}\times \mathcal{U},\Omega^{\kappa^{\mathcal{U}}}\right). \end{align*} $$
$$ \begin{align*} H^{0}\left(\mathcal{M}(\mu_{N},\mathfrak{l}\mathfrak{c})\left(\underline{v}\right)_{\mathbb{C}_{p}}\times \mathcal{U},\Omega^{\kappa^{\mathcal{U}}}\right)& \overset{p_{2}^{*}}{\to} H^{0}\left(\mathcal{Y}^{\prime}_{\mathfrak{c},\mathfrak{l}}\left(\underline{v}\right)_{\mathbb{C}_{p}}\times \mathcal{U},p_{2}^{*}\Omega^{\kappa^{\mathcal{U}}}\right)\\ & \overset{\left(\pi_{\mathfrak{l},\mathbb{C}_{p}}^{*}\right)^{-1}}{\to} H^{0}\left(\mathcal{Y}^{\prime}_{\mathfrak{c},\mathfrak{l}}\left(\underline{v}\right)_{\mathbb{C}_{p}}\times \mathcal{U},p_{1}^{*}\Omega^{\kappa^{\mathcal{U}}}\right)\\ & \overset{\mathrm{N}_{F/\mathbb{Q}}(\mathfrak{l})^{-1}\mathrm{Tr}_{p_{1}}}{\to} H^{0}\left(\mathcal{M}(\mu_{N},\mathfrak{c})(\underline{v})_{\mathbb{C}_{p}}\times \mathcal{U},\Omega^{\kappa^{\mathcal{U}}}\right). \end{align*} $$
Similarly, we have Hecke operators
![]() $T_{\mathfrak {l}}$
for
$T_{\mathfrak {l}}$
for
![]() $(\mathfrak {l},p)\neq 1$
and
$(\mathfrak {l},p)\neq 1$
and
![]() $S_{\mathfrak {l}}$
over
$S_{\mathfrak {l}}$
over
![]() $\mathbb {C}_{p}$
. We can show that they are compatible with the Hecke operators over K and that the specialization map in Lemma 3.13 is
$\mathbb {C}_{p}$
. We can show that they are compatible with the Hecke operators over K and that the specialization map in Lemma 3.13 is
![]() $\mathbf {T}$
-linear.
$\mathbf {T}$
-linear.
4 q-Expansion principle
In this section, we study the q-expansion map for arithmetic overconvergent Hilbert modular forms. We fix once and for all a representative
 $$ \begin{align*} \left[\mathrm{Cl}^{+}(F)\right]^{(p)}=\left\{\mathfrak{c}_{1}=\mathfrak{o},\mathfrak{c}_{2},\dotsc, \mathfrak{c}_{h^{+}}\right\} \end{align*} $$
$$ \begin{align*} \left[\mathrm{Cl}^{+}(F)\right]^{(p)}=\left\{\mathfrak{c}_{1}=\mathfrak{o},\mathfrak{c}_{2},\dotsc, \mathfrak{c}_{h^{+}}\right\} \end{align*} $$
of the strict class group
![]() $\mathrm {Cl}^{+}(F)$
such that every
$\mathrm {Cl}^{+}(F)$
such that every
![]() $\mathfrak {c}_{i}$
is prime to p. For any smooth
$\mathfrak {c}_{i}$
is prime to p. For any smooth
![]() $\mathbb {C}_{p}$
-affinoid variety
$\mathbb {C}_{p}$
-affinoid variety
![]() $\mathcal {U}$
, any n-analytic map
$\mathcal {U}$
, any n-analytic map
 $\mathcal {U}\to \mathcal {W}^{G}_{\mathbb {C}_{p}}$
, and any
$\mathcal {U}\to \mathcal {W}^{G}_{\mathbb {C}_{p}}$
, and any
![]() $v\in \mathbb {Q}\cap [0,B_{n})$
, we have isomorphisms
$v\in \mathbb {Q}\cap [0,B_{n})$
, we have isomorphisms
 $$ \begin{align} \begin{aligned} M^{G}\left(\mu_{N}, \left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)(v)&\simeq \bigoplus_{\mathfrak{c}\in \left[\mathrm{Cl}^{+}(F)\right]^{\left(p\right)}} M^{G}\left(\mu_{N},\mathfrak{c}, \left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)(v),\\ S^{G}\left(\mu_{N}, \left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)(v)&\simeq \bigoplus_{\mathfrak{c}\in \left[\mathrm{Cl}^{+}(F)\right]^{\left(p\right)}} S^{G}\left(\mu_{N},\mathfrak{c}, \left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)(v) \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} M^{G}\left(\mu_{N}, \left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)(v)&\simeq \bigoplus_{\mathfrak{c}\in \left[\mathrm{Cl}^{+}(F)\right]^{\left(p\right)}} M^{G}\left(\mu_{N},\mathfrak{c}, \left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)(v),\\ S^{G}\left(\mu_{N}, \left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)(v)&\simeq \bigoplus_{\mathfrak{c}\in \left[\mathrm{Cl}^{+}(F)\right]^{\left(p\right)}} S^{G}\left(\mu_{N},\mathfrak{c}, \left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)(v) \end{aligned} \end{align} $$
by which we identify both sides. For any element
 $f\in M^{G}\left (\mu _{N}, \left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )(v)$
, we write
$f\in M^{G}\left (\mu _{N}, \left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )(v)$
, we write
 $(f_{\mathfrak {c}})_{\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{\left (p\right )}}$
for the image of f by these isomorphisms. We say that f is an eigenform if it is an eigenvector for any element of
$(f_{\mathfrak {c}})_{\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{\left (p\right )}}$
for the image of f by these isomorphisms. We say that f is an eigenform if it is an eigenvector for any element of
![]() $\mathbf {T}$
.
$\mathbf {T}$
.
4.1 q-Expansion of overconvergent modular forms
For any nonzero fractional ideal
![]() $\mathfrak {c}$
of F, let us consider an unramified cusp
$\mathfrak {c}$
of F, let us consider an unramified cusp
![]() $(\mathfrak {a},\mathfrak {b},\phi )$
of
$(\mathfrak {a},\mathfrak {b},\phi )$
of
![]() $M(\mu _{N},\mathfrak {c})$
as in §3.1.2. Using any polyhedral cone decomposition
$M(\mu _{N},\mathfrak {c})$
as in §3.1.2. Using any polyhedral cone decomposition
![]() $\mathscr {C}\in \mathrm {Dec}(\mathfrak {a},\mathfrak {b})$
of
$\mathscr {C}\in \mathrm {Dec}(\mathfrak {a},\mathfrak {b})$
of
 $F^{*,+}_{\mathbb {R}}$
, we have the
$F^{*,+}_{\mathbb {R}}$
, we have the
![]() $\hat {I}_{\sigma }$
-adically complete ring
$\hat {I}_{\sigma }$
-adically complete ring
![]() $\hat {R}_{\sigma }$
and the semi-abelian scheme
$\hat {R}_{\sigma }$
and the semi-abelian scheme
![]() $\mathrm {Tate}_{\mathfrak {a},\mathfrak {b}}(q)$
over
$\mathrm {Tate}_{\mathfrak {a},\mathfrak {b}}(q)$
over
 $\bar {S}_{\sigma }=\mathrm {Spec}\left (\hat {R}_{\sigma }\right )$
for any
$\bar {S}_{\sigma }=\mathrm {Spec}\left (\hat {R}_{\sigma }\right )$
for any
![]() $\sigma \in \mathscr {C}$
.
$\sigma \in \mathscr {C}$
.
Let
 $\breve {S}_{\sigma }=\mathrm {Spf}\left (\breve {R}_{\sigma }\right )$
be the
$\breve {S}_{\sigma }=\mathrm {Spf}\left (\breve {R}_{\sigma }\right )$
be the
 $\left (p,\hat {I}_{\sigma }\right )$
-adic formal completion of
$\left (p,\hat {I}_{\sigma }\right )$
-adic formal completion of
![]() $\hat {S}_{\sigma }$
. The smoothness assumption on
$\hat {S}_{\sigma }$
. The smoothness assumption on
![]() $\mathscr {C}$
implies that there exists a basis
$\mathscr {C}$
implies that there exists a basis
![]() $\xi _{1},\dotsc ,\xi _{g}$
of the
$\xi _{1},\dotsc ,\xi _{g}$
of the
![]() $\mathbb {Z}$
-module
$\mathbb {Z}$
-module
![]() $\mathfrak {a}\mathfrak {b}$
satisfying
$\mathfrak {a}\mathfrak {b}$
satisfying
with some r. For any ring B, we write
 $$ \begin{align*} B\left[X_{\leq r}, X^{\pm}_{>r}\right]:=B\left[X_{1},\dotsc,X_{r},X_{r+1}^{\pm},\dotsc,X_{g}^{\pm}\right]. \end{align*} $$
$$ \begin{align*} B\left[X_{\leq r}, X^{\pm}_{>r}\right]:=B\left[X_{1},\dotsc,X_{r},X_{r+1}^{\pm},\dotsc,X_{g}^{\pm}\right]. \end{align*} $$
For any extension
![]() $L/K$
of complete valuation fields, we denote the p-adic completion of
$L/K$
of complete valuation fields, we denote the p-adic completion of
 $\mathcal {O}_{L}\left [X_{\leq r}, X^{\pm }_{>r}\right ]$
by
$\mathcal {O}_{L}\left [X_{\leq r}, X^{\pm }_{>r}\right ]$
by
 $\mathcal {O}_{L}\left \langle X_{\leq r}, X^{\pm }_{>r}\right \rangle $
and put
$\mathcal {O}_{L}\left \langle X_{\leq r}, X^{\pm }_{>r}\right \rangle $
and put
 $$ \begin{align*} L\left\langle X_{\leq r}, X^{\pm}_{>r} \right\rangle=\mathcal{O}_{L}\left\langle X_{\leq r}, X^{\pm}_{>r}\right\rangle[1/p]. \end{align*} $$
$$ \begin{align*} L\left\langle X_{\leq r}, X^{\pm}_{>r} \right\rangle=\mathcal{O}_{L}\left\langle X_{\leq r}, X^{\pm}_{>r}\right\rangle[1/p]. \end{align*} $$
Then the
![]() $\mathcal {O}_{K}$
-algebra
$\mathcal {O}_{K}$
-algebra
![]() $\hat {R}_{\sigma }$
is isomorphic to the completion of the ring
$\hat {R}_{\sigma }$
is isomorphic to the completion of the ring
 $\mathcal {O}_{K}\left [X_{\leq r}, X^{\pm }_{>r}\right ]$
with respect to the principal ideal
$\mathcal {O}_{K}\left [X_{\leq r}, X^{\pm }_{>r}\right ]$
with respect to the principal ideal
![]() $(X_{1}\dotsm X_{r})$
via the map
$(X_{1}\dotsm X_{r})$
via the map
![]() $X_{i}\mapsto q^{\xi _{i}}$
, and the ring
$X_{i}\mapsto q^{\xi _{i}}$
, and the ring
![]() $\breve {R}_{\sigma }$
is isomorphic to the p-adic completion of
$\breve {R}_{\sigma }$
is isomorphic to the p-adic completion of
![]() $\hat {R}_{\sigma }$
. Hence the ring
$\hat {R}_{\sigma }$
. Hence the ring
![]() $\breve {R}_{\sigma }$
is normal and the formal scheme
$\breve {R}_{\sigma }$
is normal and the formal scheme
![]() $\breve {S}_{\sigma }$
is an object of the category
$\breve {S}_{\sigma }$
is an object of the category
![]() $\mathrm {FS} {}_{\mathcal {O}_{K}}$
of [Reference de Jong19, Definition 7.0.1]. In fact, the ring
$\mathrm {FS} {}_{\mathcal {O}_{K}}$
of [Reference de Jong19, Definition 7.0.1]. In fact, the ring
![]() $\breve {R}_{\sigma }$
is isomorphic to the ring
$\breve {R}_{\sigma }$
is isomorphic to the ring
 $$ \begin{align} \mathcal{O}_{K}\left\langle X_{\leq r}, X^{\pm}_{>r}\right\rangle [[Z]]/(Z-X_{1}\dotsm X_{r}). \end{align} $$
$$ \begin{align} \mathcal{O}_{K}\left\langle X_{\leq r}, X^{\pm}_{>r}\right\rangle [[Z]]/(Z-X_{1}\dotsm X_{r}). \end{align} $$
Moreover, since the natural map
 $$ \begin{align*} &\mathcal{O}_{K,m}\left[X_{\leq r}, X^{\pm}_{>r}\right]/(X_{1}\dotsm X_{r})^{n} \to \\ &\qquad\qquad\qquad\qquad\qquad\qquad\mathcal{O}_{K,m}\left[X_{r+1}^{\pm},\dotsc,X_{g}^{\pm}\right][[X_{1},\dotsc,X_{r}]]/(X_{1}\dotsm X_{r})^{n} \end{align*} $$
$$ \begin{align*} &\mathcal{O}_{K,m}\left[X_{\leq r}, X^{\pm}_{>r}\right]/(X_{1}\dotsm X_{r})^{n} \to \\ &\qquad\qquad\qquad\qquad\qquad\qquad\mathcal{O}_{K,m}\left[X_{r+1}^{\pm},\dotsc,X_{g}^{\pm}\right][[X_{1},\dotsc,X_{r}]]/(X_{1}\dotsm X_{r})^{n} \end{align*} $$
is injective for any positive integer m, by taking the limit we may identify the rings
![]() $\hat {R}_{\sigma }$
and
$\hat {R}_{\sigma }$
and
![]() $\breve {R}_{\sigma }$
with
$\breve {R}_{\sigma }$
with
![]() $\mathcal {O}_{K}$
-subalgebras of the
$\mathcal {O}_{K}$
-subalgebras of the
![]() $\mathcal {O}_{K}$
-algebra
$\mathcal {O}_{K}$
-algebra
 $$ \begin{align*} \mathcal{O}_{K}\left\langle q^{\pm\xi_{r+1}},\dotsc, q^{\pm\xi_{g}}\right\rangle\left[\left[q^{\xi_{1}},\dotsc,q^{\xi_{r}}\right]\right]. \end{align*} $$
$$ \begin{align*} \mathcal{O}_{K}\left\langle q^{\pm\xi_{r+1}},\dotsc, q^{\pm\xi_{g}}\right\rangle\left[\left[q^{\xi_{1}},\dotsc,q^{\xi_{r}}\right]\right]. \end{align*} $$
We denote by
 $\breve {S}_{\sigma }^{\mathrm {rig}}$
the Berthelot generic fiber of
$\breve {S}_{\sigma }^{\mathrm {rig}}$
the Berthelot generic fiber of
![]() $\breve {S}_{\sigma }$
. Similarly, we denote by
$\breve {S}_{\sigma }$
. Similarly, we denote by
![]() $\breve {S}_{\mathscr {C}}$
and
$\breve {S}_{\mathscr {C}}$
and
 $\breve {S}^{\mathrm {rig}}_{\mathscr {C}}$
the formal completion of
$\breve {S}^{\mathrm {rig}}_{\mathscr {C}}$
the formal completion of
![]() $\hat {S}_{\mathscr {C}}$
along the boundary of the special fiber and its Berthelot generic fiber. From the definition, we have formal open and admissible coverings
$\hat {S}_{\mathscr {C}}$
along the boundary of the special fiber and its Berthelot generic fiber. From the definition, we have formal open and admissible coverings
 $$ \begin{align*} \breve{S}_{\mathscr{C}}=\bigcup_{\sigma\in \mathscr{C}} \breve{S}_{\sigma},\qquad \breve{S}^{\mathrm{rig}}_{\mathscr{C}}=\bigcup_{\sigma\in \mathscr{C}} \breve{S}^{\mathrm{rig}}_{\sigma}. \end{align*} $$
$$ \begin{align*} \breve{S}_{\mathscr{C}}=\bigcup_{\sigma\in \mathscr{C}} \breve{S}_{\sigma},\qquad \breve{S}^{\mathrm{rig}}_{\mathscr{C}}=\bigcup_{\sigma\in \mathscr{C}} \breve{S}^{\mathrm{rig}}_{\sigma}. \end{align*} $$
Since the quotient of
![]() $\hat {S}_{\mathscr {C}}$
by the action of
$\hat {S}_{\mathscr {C}}$
by the action of
![]() $U_{N}$
is obtained by a regluing, so is the quotient
$U_{N}$
is obtained by a regluing, so is the quotient
 $\breve {S}_{\mathscr {C}}/U_{N}$
, and this coincides with the formal completion of
$\breve {S}_{\mathscr {C}}/U_{N}$
, and this coincides with the formal completion of
 $\hat {S}_{\mathscr {C}}/U_{N}$
along the boundary of the special fiber.
$\hat {S}_{\mathscr {C}}/U_{N}$
along the boundary of the special fiber.
Consider the case
![]() $\mathscr {C}=\mathscr {C}(\mathfrak {a},\mathfrak {b})$
. Since the map
$\mathscr {C}=\mathscr {C}(\mathfrak {a},\mathfrak {b})$
. Since the map
![]() $\bar {S}_{\sigma }\to \bar {M}(\mu _{N},\mathfrak {c})$
defined using
$\bar {S}_{\sigma }\to \bar {M}(\mu _{N},\mathfrak {c})$
defined using
![]() $\mathrm {Tate}_{\mathfrak {a},\mathfrak {b}}(q)$
induces an open immersion
$\mathrm {Tate}_{\mathfrak {a},\mathfrak {b}}(q)$
induces an open immersion
 $$ \begin{align*} \coprod \hat{S}_{\mathscr{C}(\mathfrak{a},\mathfrak{b})}/U_{N} \to \bar{M}(\mu_{N},\mathfrak{c})\rvert_{D}^{\wedge} \end{align*} $$
$$ \begin{align*} \coprod \hat{S}_{\mathscr{C}(\mathfrak{a},\mathfrak{b})}/U_{N} \to \bar{M}(\mu_{N},\mathfrak{c})\rvert_{D}^{\wedge} \end{align*} $$
to the formal completion of
![]() $\bar {M}(\mu _{N},\mathfrak {c})\rvert _{D}^{\wedge }$
of
$\bar {M}(\mu _{N},\mathfrak {c})\rvert _{D}^{\wedge }$
of
![]() $\bar {M}(\mu _{N},\mathfrak {c})$
along the boundary divisor D, taking the formal completion we obtain an open immersion
$\bar {M}(\mu _{N},\mathfrak {c})$
along the boundary divisor D, taking the formal completion we obtain an open immersion
 $$ \begin{align*} \coprod \breve{S}_{\mathscr{C}(\mathfrak{a},\mathfrak{b})}/U_{N} \to \bar{\mathfrak{M}}(\mu_{N},\mathfrak{c})\rvert_{D_{k}}^{\wedge} \end{align*} $$
$$ \begin{align*} \coprod \breve{S}_{\mathscr{C}(\mathfrak{a},\mathfrak{b})}/U_{N} \to \bar{\mathfrak{M}}(\mu_{N},\mathfrak{c})\rvert_{D_{k}}^{\wedge} \end{align*} $$
to the formal completion
 $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})\rvert _{D_{k}}^{\wedge }$
of
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})\rvert _{D_{k}}^{\wedge }$
of
![]() $\bar {M}(\mu _{N},\mathfrak {c})$
along the boundary
$\bar {M}(\mu _{N},\mathfrak {c})$
along the boundary
![]() $D_{k}$
of the special fiber. Let
$D_{k}$
of the special fiber. Let
![]() $\mathrm {sp}: \bar {\mathcal {M}}(\mu _{N},\mathfrak {c})\to \bar {M}(\mu _{N},\mathfrak {c})_{k}$
be the specialization map with respect to
$\mathrm {sp}: \bar {\mathcal {M}}(\mu _{N},\mathfrak {c})\to \bar {M}(\mu _{N},\mathfrak {c})_{k}$
be the specialization map with respect to
![]() $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})$
. Then [Reference de Jong19, Lemma 7.2.5] implies
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})$
. Then [Reference de Jong19, Lemma 7.2.5] implies
 $\left (\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})\rvert _{D_{k}}^{\wedge }\right )^{\mathrm {rig}}=\mathrm {sp}^{-1}(D_{k})$
.
$\left (\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})\rvert _{D_{k}}^{\wedge }\right )^{\mathrm {rig}}=\mathrm {sp}^{-1}(D_{k})$
.
Let
 $\breve {S}^{\mathrm {rig}}_{\sigma , \mathbb {C}_{p}}$
and
$\breve {S}^{\mathrm {rig}}_{\sigma , \mathbb {C}_{p}}$
and
 $\breve {S}^{\mathrm {rig}}_{\mathscr {C}, \mathbb {C}_{p}}$
be the base extensions to
$\breve {S}^{\mathrm {rig}}_{\mathscr {C}, \mathbb {C}_{p}}$
be the base extensions to
![]() $\mathrm {Sp}\left (\mathbb {C}_{p}\right )$
of
$\mathrm {Sp}\left (\mathbb {C}_{p}\right )$
of
 $\breve {S}^{\mathrm {rig}}_{\sigma }$
and
$\breve {S}^{\mathrm {rig}}_{\sigma }$
and
 $\breve {S}^{\mathrm {rig}}_{\mathscr {C}}$
, respectively. Note that
$\breve {S}^{\mathrm {rig}}_{\mathscr {C}}$
, respectively. Note that
 $\breve {S}^{\mathrm {rig}}_{\sigma ,\mathbb {C}_{p}}$
can be identified with the rigid analytic variety over
$\breve {S}^{\mathrm {rig}}_{\sigma ,\mathbb {C}_{p}}$
can be identified with the rigid analytic variety over
![]() $\mathbb {C}_{p}$
whose set of
$\mathbb {C}_{p}$
whose set of
![]() $\mathbb {C}_{p}$
-points is
$\mathbb {C}_{p}$
-points is
 $$ \begin{align} \left\{\left(x_{1},\dotsc,x_{g}\right)\in \mathbb{C}_{p}^{g}\ \middle| \begin{array}{cc} x_{i}\in \mathcal{O}_{\mathbb{C}_{p}}\ (i\leq r),\ x_{i}\in \mathcal{O}^{\times}_{\mathbb{C}_{p}}\ (i> r), \\ x_{1}\dotsm x_{r}\in m_{\mathbb{C}_{p}} \end{array} \!\!\!\!\!\right\} \end{align} $$
$$ \begin{align} \left\{\left(x_{1},\dotsc,x_{g}\right)\in \mathbb{C}_{p}^{g}\ \middle| \begin{array}{cc} x_{i}\in \mathcal{O}_{\mathbb{C}_{p}}\ (i\leq r),\ x_{i}\in \mathcal{O}^{\times}_{\mathbb{C}_{p}}\ (i> r), \\ x_{1}\dotsm x_{r}\in m_{\mathbb{C}_{p}} \end{array} \!\!\!\!\!\right\} \end{align} $$
for r as before. Then, with the notation of [Reference Conrad18, Theorem 3.1.5], we have
 $$ \begin{align*} \left(\breve{S}_{\sigma}\right)^{\mathrm{rig}}_{/\mathbb{C}_{p}}=\breve{S}^{\mathrm{rig}}_{\sigma, \mathbb{C}_{p}},\qquad \left(\breve{S}_{\mathscr{C}}\right)^{\mathrm{rig}}_{/\mathbb{C}_{p}}=\breve{S}^{\mathrm{rig}}_{\mathscr{C}, \mathbb{C}_{p}}. \end{align*} $$
$$ \begin{align*} \left(\breve{S}_{\sigma}\right)^{\mathrm{rig}}_{/\mathbb{C}_{p}}=\breve{S}^{\mathrm{rig}}_{\sigma, \mathbb{C}_{p}},\qquad \left(\breve{S}_{\mathscr{C}}\right)^{\mathrm{rig}}_{/\mathbb{C}_{p}}=\breve{S}^{\mathrm{rig}}_{\mathscr{C}, \mathbb{C}_{p}}. \end{align*} $$
Since the functor
 $(-)^{\mathrm {rig}}_{/\mathbb {C}_{p}}$
sends formal open immersions to open immersions and formal open coverings to admissible coverings, each
$(-)^{\mathrm {rig}}_{/\mathbb {C}_{p}}$
sends formal open immersions to open immersions and formal open coverings to admissible coverings, each
 $\breve {S}^{\mathrm {rig}}_{\sigma ,\mathbb {C}_{p}}$
is an admissible open subset of
$\breve {S}^{\mathrm {rig}}_{\sigma ,\mathbb {C}_{p}}$
is an admissible open subset of
 $\breve {S}^{\mathrm {rig}}_{\mathscr {C},\mathbb {C}_{p}}$
such that
$\breve {S}^{\mathrm {rig}}_{\mathscr {C},\mathbb {C}_{p}}$
such that
 $\breve {S}^{\mathrm {rig}}_{\mathscr {C},\mathbb {C}_{p}}=\bigcup _{\sigma \in \mathscr {C}} \breve {S}^{\mathrm {rig}}_{\sigma ,\mathbb {C}_{p}}$
is an admissible covering. Moreover, we have
$\breve {S}^{\mathrm {rig}}_{\mathscr {C},\mathbb {C}_{p}}=\bigcup _{\sigma \in \mathscr {C}} \breve {S}^{\mathrm {rig}}_{\sigma ,\mathbb {C}_{p}}$
is an admissible covering. Moreover, we have
 $$ \begin{align*} \left(\breve{S}_{\mathscr{C}}/U_{N}\right)^{\mathrm{rig}}_{/\mathbb{C}_{p}}=\breve{S}^{\mathrm{rig}}_{\mathscr{C},\mathbb{C}_{p}}/U_{N}. \end{align*} $$
$$ \begin{align*} \left(\breve{S}_{\mathscr{C}}/U_{N}\right)^{\mathrm{rig}}_{/\mathbb{C}_{p}}=\breve{S}^{\mathrm{rig}}_{\mathscr{C},\mathbb{C}_{p}}/U_{N}. \end{align*} $$
Note that the formation of the tube
![]() $\mathrm {sp}^{-1}(D_{k})$
is compatible with the base extension to
$\mathrm {sp}^{-1}(D_{k})$
is compatible with the base extension to
![]() $\mathbb {C}_{p}$
[Reference Berthelot9, Proposition 1.1.13]. Thus, for
$\mathbb {C}_{p}$
[Reference Berthelot9, Proposition 1.1.13]. Thus, for
![]() $\mathscr {C}=\mathscr {C}(\mathfrak {a},\mathfrak {b})$
, we obtain maps
$\mathscr {C}=\mathscr {C}(\mathfrak {a},\mathfrak {b})$
, we obtain maps
 $$ \begin{align} \coprod_{\sigma\in \mathscr{C}} \breve{S}^{\mathrm{rig}}_{\sigma,\mathbb{C}_{p}} \to \breve{S}_{\mathscr{C},\mathbb{C}_{p}}^{\mathrm{rig}}/U_{N} \to \bar{\mathcal{M}}(\mu_{N},\mathfrak{c})_{\mathbb{C}_{p}}, \end{align} $$
$$ \begin{align} \coprod_{\sigma\in \mathscr{C}} \breve{S}^{\mathrm{rig}}_{\sigma,\mathbb{C}_{p}} \to \breve{S}_{\mathscr{C},\mathbb{C}_{p}}^{\mathrm{rig}}/U_{N} \to \bar{\mathcal{M}}(\mu_{N},\mathfrak{c})_{\mathbb{C}_{p}}, \end{align} $$
where the first map is a surjective local isomorphism and the second is an open immersion factoring through
![]() $\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})(0)_{\mathbb {C}_{p}}$
.
$\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})(0)_{\mathbb {C}_{p}}$
.
We denote by
 $\breve {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
,
$\breve {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
,
 $\breve {S}_{\sigma , \mathcal {O}_{\mathbb {C}_{p}}}$
, and
$\breve {S}_{\sigma , \mathcal {O}_{\mathbb {C}_{p}}}$
, and
 $\breve {S}_{\mathscr {C}, \mathcal {O}_{\mathbb {C}_{p}}}$
the base extensions to
$\breve {S}_{\mathscr {C}, \mathcal {O}_{\mathbb {C}_{p}}}$
the base extensions to
 $\mathrm {Spf}\left (\mathcal {O}_{\mathbb {C}_{p}}\right )$
of
$\mathrm {Spf}\left (\mathcal {O}_{\mathbb {C}_{p}}\right )$
of
![]() $\breve {R}_{\sigma }$
,
$\breve {R}_{\sigma }$
,
![]() $\breve {S}_{\sigma }$
, and
$\breve {S}_{\sigma }$
, and
![]() $\breve {S}_{\mathscr {C}}$
, respectively. From the identification (4.2), we can show
$\breve {S}_{\mathscr {C}}$
, respectively. From the identification (4.2), we can show
 $$ \begin{align} \breve{R}_{\sigma,\mathcal{O}_{\mathbb{C}_{p}}}=\mathcal{O}_{\mathbb{C}_{p}}\left\langle X_{\leq r}, X^{\pm}_{>r}\right\rangle [[Z]]/(Z-X_{1}\dotsm X_{r}). \end{align} $$
$$ \begin{align} \breve{R}_{\sigma,\mathcal{O}_{\mathbb{C}_{p}}}=\mathcal{O}_{\mathbb{C}_{p}}\left\langle X_{\leq r}, X^{\pm}_{>r}\right\rangle [[Z]]/(Z-X_{1}\dotsm X_{r}). \end{align} $$
Indeed, first note that the ring
 $\breve {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
is isomorphic to
$\breve {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
is isomorphic to
 $$ \begin{align} \varprojlim_{n\geq 0}\varprojlim_{m\geq 0} \mathcal{O}_{\mathbb{C}_{p},n}\left[X_{\leq r}, X^{\pm}_{>r},Z\right]/(Z-X_{1}\dotsm X_{r}, Z^{m}). \end{align} $$
$$ \begin{align} \varprojlim_{n\geq 0}\varprojlim_{m\geq 0} \mathcal{O}_{\mathbb{C}_{p},n}\left[X_{\leq r}, X^{\pm}_{>r},Z\right]/(Z-X_{1}\dotsm X_{r}, Z^{m}). \end{align} $$
Since the ring
 $$ \begin{align*} \mathcal{O}_{\mathbb{C}_{p},n}\left[X_{\leq r}, X^{\pm}_{>r},Z\right]/(Z-X_{1}\dotsm X_{r}) \end{align*} $$
$$ \begin{align*} \mathcal{O}_{\mathbb{C}_{p},n}\left[X_{\leq r}, X^{\pm}_{>r},Z\right]/(Z-X_{1}\dotsm X_{r}) \end{align*} $$
is Z-torsion free, its Z-adic completion is
 $$ \begin{align*} \mathcal{O}_{\mathbb{C}_{p},n}\left[X_{\leq r}, X^{\pm}_{>r}\right][[Z]]/(Z-X_{1}\dotsm X_{r}). \end{align*} $$
$$ \begin{align*} \mathcal{O}_{\mathbb{C}_{p},n}\left[X_{\leq r}, X^{\pm}_{>r}\right][[Z]]/(Z-X_{1}\dotsm X_{r}). \end{align*} $$
Similarly, since an elementary argument shows that the ring
 $$ \begin{align*} \mathcal{O}_{\mathbb{C}_{p}}\left[X_{\leq r}, X^{\pm}_{>r}\right][[Z]]/(Z-X_{1}\dotsm X_{r}) \end{align*} $$
$$ \begin{align*} \mathcal{O}_{\mathbb{C}_{p}}\left[X_{\leq r}, X^{\pm}_{>r}\right][[Z]]/(Z-X_{1}\dotsm X_{r}) \end{align*} $$
is p-torsion free, taking the p-adic completion yields the claim. (The reason for this ad hoc proof is that in general we do not know if the completion is compatible with quotients for non-quasi-idyllic rings.)
Lemma 4.1. For any extension
![]() $L/K$
of complete valuation fields with residue field
$L/K$
of complete valuation fields with residue field
![]() $k_{L}$
, the rings
$k_{L}$
, the rings
 $$ \begin{align*} \mathcal{O}_{L}\left\langle X_{\leq r}, X^{\pm}_{>r}\right\rangle [[Z]]/(Z-X_{1}\dotsm X_{r}),\qquad k_{L}\left[X_{\leq r}, X^{\pm}_{>r}\right] [[Z]]/(Z-X_{1}\dotsm X_{r}) \end{align*} $$
$$ \begin{align*} \mathcal{O}_{L}\left\langle X_{\leq r}, X^{\pm}_{>r}\right\rangle [[Z]]/(Z-X_{1}\dotsm X_{r}),\qquad k_{L}\left[X_{\leq r}, X^{\pm}_{>r}\right] [[Z]]/(Z-X_{1}\dotsm X_{r}) \end{align*} $$
are integral domains. In particular, the ring
 $\breve {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
is an integral domain.
$\breve {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
is an integral domain.
Proof. For the former ring, we can show that it is a subring of the ring
 $$ \begin{align*} \breve{R}_{L}:=L\left\langle X_{\leq r}, X^{\pm}_{>r} \right\rangle [[Z]]/(Z-X_{1}\dotsm X_{r}). \end{align*} $$
$$ \begin{align*} \breve{R}_{L}:=L\left\langle X_{\leq r}, X^{\pm}_{>r} \right\rangle [[Z]]/(Z-X_{1}\dotsm X_{r}). \end{align*} $$
It suffices to show that
![]() $\breve {R}_{L}$
is an integral domain. Since the ring
$\breve {R}_{L}$
is an integral domain. Since the ring
 $L\left \langle X_{\leq r}, X^{\pm }_{>r}\right \rangle $
is Noetherian and normal, the ring
$L\left \langle X_{\leq r}, X^{\pm }_{>r}\right \rangle $
is Noetherian and normal, the ring
![]() $\breve {R}_{L}$
is also normal. Since
$\breve {R}_{L}$
is also normal. Since
![]() $\breve {R}_{L}$
is Z-adically complete and Z-torsion free and
$\breve {R}_{L}$
is Z-adically complete and Z-torsion free and
 $\mathrm {Spec}\left (\breve {R}_{L}/(Z)\right )$
is connected, we see that
$\mathrm {Spec}\left (\breve {R}_{L}/(Z)\right )$
is connected, we see that
 $\mathrm {Spec}\left (\breve {R}_{L}\right )$
is also connected, and the lemma follows. We can show the assertion on the latter ring similarly.
$\mathrm {Spec}\left (\breve {R}_{L}\right )$
is also connected, and the lemma follows. We can show the assertion on the latter ring similarly.
From the description (4.3) of
 $\breve {S}_{\sigma ,\mathbb {C}_{p}}^{\mathrm {rig}}$
, we see that there exists an inclusion
$\breve {S}_{\sigma ,\mathbb {C}_{p}}^{\mathrm {rig}}$
, we see that there exists an inclusion
 $$ \begin{align*} \mathcal{O}\left(\breve{S}_{\sigma,\mathcal{O}_{\mathbb{C}_{p}}}\right)=\breve{R}_{\sigma,\mathcal{O}_{\mathbb{C}_{p}}}\subseteq \mathcal{O}^{\circ}\left(\breve{S}^{\mathrm{rig}}_{\sigma,\mathbb{C}_{p}}\right). \end{align*} $$
$$ \begin{align*} \mathcal{O}\left(\breve{S}_{\sigma,\mathcal{O}_{\mathbb{C}_{p}}}\right)=\breve{R}_{\sigma,\mathcal{O}_{\mathbb{C}_{p}}}\subseteq \mathcal{O}^{\circ}\left(\breve{S}^{\mathrm{rig}}_{\sigma,\mathbb{C}_{p}}\right). \end{align*} $$
By gluing, this yields an inclusion
 $$ \begin{align} \mathcal{O}\left(\breve{S}_{\mathscr{C},\mathcal{O}_{\mathbb{C}_{p}}}\right) \subseteq \mathcal{O}^{\circ}\left(\breve{S}_{\mathscr{C},\mathbb{C}_{p}}^{\mathrm{rig}}\right). \end{align} $$
$$ \begin{align} \mathcal{O}\left(\breve{S}_{\mathscr{C},\mathcal{O}_{\mathbb{C}_{p}}}\right) \subseteq \mathcal{O}^{\circ}\left(\breve{S}_{\mathscr{C},\mathbb{C}_{p}}^{\mathrm{rig}}\right). \end{align} $$
By the description (4.6) of the ring
 $\breve {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
, we have a natural inclusion
$\breve {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
, we have a natural inclusion
 $$ \begin{align} \breve{R}_{\sigma,\mathcal{O}_{\mathbb{C}_{p}}} \subseteq \prod_{\xi\in \mathfrak{a}\mathfrak{b}} \mathcal{O}_{\mathbb{C}_{p}} q^{\xi}, \end{align} $$
$$ \begin{align} \breve{R}_{\sigma,\mathcal{O}_{\mathbb{C}_{p}}} \subseteq \prod_{\xi\in \mathfrak{a}\mathfrak{b}} \mathcal{O}_{\mathbb{C}_{p}} q^{\xi}, \end{align} $$
which is compatible with the restriction map
 $\breve {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}} \to \breve {R}_{\sigma ^{\prime },\mathcal {O}_{\mathbb {C}_{p}}}$
for any
$\breve {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}} \to \breve {R}_{\sigma ^{\prime },\mathcal {O}_{\mathbb {C}_{p}}}$
for any
![]() $\sigma $
and
$\sigma $
and
![]() $\sigma ^{\prime }$
such that
$\sigma ^{\prime }$
such that
![]() $\sigma ^{\prime }$
is a face of the closure
$\sigma ^{\prime }$
is a face of the closure
![]() $\bar {\sigma }$
. Then we have an isomorphism
$\bar {\sigma }$
. Then we have an isomorphism
 $$ \begin{align*} \mathcal{O}\left(\breve{S}_{\mathscr{C},\mathcal{O}_{\mathbb{C}_{p}}}\right)\simeq \bigcap_{\sigma\in \mathscr{C}} \breve{R}_{\sigma,\mathcal{O}_{\mathbb{C}_{p}}}. \end{align*} $$
$$ \begin{align*} \mathcal{O}\left(\breve{S}_{\mathscr{C},\mathcal{O}_{\mathbb{C}_{p}}}\right)\simeq \bigcap_{\sigma\in \mathscr{C}} \breve{R}_{\sigma,\mathcal{O}_{\mathbb{C}_{p}}}. \end{align*} $$
Note that if the dimension of the
![]() $\mathbb {R}$
-vector space
$\mathbb {R}$
-vector space
![]() $\mathrm {Span}_{\mathbb {R}}(\sigma )$
generated by the elements of
$\mathrm {Span}_{\mathbb {R}}(\sigma )$
generated by the elements of
![]() $\sigma $
is g, then we have
$\sigma $
is g, then we have
with some
![]() $\xi _{1},\dotsc ,\xi _{g}\in \mathfrak {a}\mathfrak {b}$
. Thus any element of
$\xi _{1},\dotsc ,\xi _{g}\in \mathfrak {a}\mathfrak {b}$
. Thus any element of
 $\breve {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
is a formal power series of
$\breve {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
is a formal power series of
![]() $q^{\xi _{1}},\dotsc ,q^{\xi _{g}}$
and the ring
$q^{\xi _{1}},\dotsc ,q^{\xi _{g}}$
and the ring
 $\mathcal {O}_{\mathbb {C}_{p}}\left [\left [q^{\xi }\mid \xi \in (\mathfrak {a}\mathfrak {b})\cap \sigma ^{\vee }\right ]\right ]$
can be identified with the subset
$\mathcal {O}_{\mathbb {C}_{p}}\left [\left [q^{\xi }\mid \xi \in (\mathfrak {a}\mathfrak {b})\cap \sigma ^{\vee }\right ]\right ]$
can be identified with the subset
 $$ \begin{align*} \left\{\left(a_{\xi} q^{\xi}\right)_{\xi \in \mathfrak{a}\mathfrak{b}}\in \prod_{\xi\in \mathfrak{a}\mathfrak{b}} \mathcal{O}_{\mathbb{C}_{p}} q^{\xi} \mid a_{\xi}=0\ \text{ for any } \xi\notin (\mathfrak{a}\mathfrak{b})\cap \sigma^{\vee} \right\}. \end{align*} $$
$$ \begin{align*} \left\{\left(a_{\xi} q^{\xi}\right)_{\xi \in \mathfrak{a}\mathfrak{b}}\in \prod_{\xi\in \mathfrak{a}\mathfrak{b}} \mathcal{O}_{\mathbb{C}_{p}} q^{\xi} \mid a_{\xi}=0\ \text{ for any } \xi\notin (\mathfrak{a}\mathfrak{b})\cap \sigma^{\vee} \right\}. \end{align*} $$
From the equality
 $$ \begin{align*} (\mathfrak{a}\mathfrak{b})^{+}\cup \{0\}=\bigcap\left\{(\mathfrak{a}\mathfrak{b})\cap \sigma^{\vee}\mid \sigma\in\mathscr{C},\ \dim_{\mathbb{R}}(\mathrm{Span}_{\mathbb{R}}(\sigma))=g\right\}, \end{align*} $$
$$ \begin{align*} (\mathfrak{a}\mathfrak{b})^{+}\cup \{0\}=\bigcap\left\{(\mathfrak{a}\mathfrak{b})\cap \sigma^{\vee}\mid \sigma\in\mathscr{C},\ \dim_{\mathbb{R}}(\mathrm{Span}_{\mathbb{R}}(\sigma))=g\right\}, \end{align*} $$
we have an inclusion
 $$ \begin{align*} \mathcal{O}_{\mathbb{C}_{p}}\left[\left[q^{\xi} \mid \xi\in (\mathfrak{a}\mathfrak{b})^{+}\cup\{0\}\right]\right]\supseteq \mathcal{O}\left(\breve{S}_{\mathscr{C},\mathcal{O}_{\mathbb{C}_{p}}}\right). \end{align*} $$
$$ \begin{align*} \mathcal{O}_{\mathbb{C}_{p}}\left[\left[q^{\xi} \mid \xi\in (\mathfrak{a}\mathfrak{b})^{+}\cup\{0\}\right]\right]\supseteq \mathcal{O}\left(\breve{S}_{\mathscr{C},\mathcal{O}_{\mathbb{C}_{p}}}\right). \end{align*} $$
On the other hand, if we identify
 $$ \begin{align*} F_{\mathbb{R}}\simeq \prod_{\beta\in \mathrm{Hom}_{\mathbb{Q}\text{-alg.}}(F,\mathbb{R})} \mathbb{R},\quad x\otimes 1\mapsto (\beta(x))_{\beta}, \end{align*} $$
$$ \begin{align*} F_{\mathbb{R}}\simeq \prod_{\beta\in \mathrm{Hom}_{\mathbb{Q}\text{-alg.}}(F,\mathbb{R})} \mathbb{R},\quad x\otimes 1\mapsto (\beta(x))_{\beta}, \end{align*} $$
then every boundary
![]() $\tau $
of
$\tau $
of
![]() $\sigma ^{\vee }$
is outside the closure of the positive cone
$\sigma ^{\vee }$
is outside the closure of the positive cone
 $F_{\mathbb {R}}^{\times ,+}$
of
$F_{\mathbb {R}}^{\times ,+}$
of
![]() $F_{\mathbb {R}}$
. Hence for any positive real number
$F_{\mathbb {R}}$
. Hence for any positive real number
![]() $\rho $
, the number of elements
$\rho $
, the number of elements
![]() $\xi $
of
$\xi $
of
![]() $(\mathfrak {a}\mathfrak {b})^{+}$
such that the distance from
$(\mathfrak {a}\mathfrak {b})^{+}$
such that the distance from
![]() $\xi $
to
$\xi $
to
![]() $\tau $
is less than
$\tau $
is less than
![]() $\rho $
is finite. This implies that any element of
$\rho $
is finite. This implies that any element of
 $\mathcal {O}_{\mathbb {C}_{p}}\left [\left [q^{\xi }\mid \xi \in (\mathfrak {a}\mathfrak {b})^{+}\cup \{0\}\right ]\right ]$
is contained in the completion of the ring
$\mathcal {O}_{\mathbb {C}_{p}}\left [\left [q^{\xi }\mid \xi \in (\mathfrak {a}\mathfrak {b})^{+}\cup \{0\}\right ]\right ]$
is contained in the completion of the ring
 $$ \begin{align*} \mathcal{O}_{\mathbb{C}_{p}}\left[q^{\xi_{1}},\dotsc, q^{\xi_{r}},q^{\pm \xi_{r+1}},\dotsc, q^{\pm \xi_{g}}\right] \end{align*} $$
$$ \begin{align*} \mathcal{O}_{\mathbb{C}_{p}}\left[q^{\xi_{1}},\dotsc, q^{\xi_{r}},q^{\pm \xi_{r+1}},\dotsc, q^{\pm \xi_{g}}\right] \end{align*} $$
with respect to the
![]() $q^{\xi _{1}}\dotsm q^{\xi _{r}}$
-adic topology. We can see that this completion is contained in
$q^{\xi _{1}}\dotsm q^{\xi _{r}}$
-adic topology. We can see that this completion is contained in
 $\breve {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
. Therefore, we obtain an identification
$\breve {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
. Therefore, we obtain an identification
 $$ \begin{align*} \mathcal{O}_{\mathbb{C}_{p}}\left[\left[q^{\xi}\mid \xi\in (\mathfrak{a}\mathfrak{b})^{+}\cup\{0\}\right]\right]\simeq \mathcal{O}\left(\breve{S}_{\mathscr{C},\mathcal{O}_{\mathbb{C}_{p}}}\right), \end{align*} $$
$$ \begin{align*} \mathcal{O}_{\mathbb{C}_{p}}\left[\left[q^{\xi}\mid \xi\in (\mathfrak{a}\mathfrak{b})^{+}\cup\{0\}\right]\right]\simeq \mathcal{O}\left(\breve{S}_{\mathscr{C},\mathcal{O}_{\mathbb{C}_{p}}}\right), \end{align*} $$
which is compatible with the inclusion (4.8).
Let
![]() $\mathfrak {c}$
be any nonzero fractional ideal of F and let
$\mathfrak {c}$
be any nonzero fractional ideal of F and let
![]() $\mathfrak {a},\mathfrak {b}$
be fractional ideals satisfying
$\mathfrak {a},\mathfrak {b}$
be fractional ideals satisfying
![]() $\mathfrak {a}\mathfrak {b}^{-1}=\mathfrak {c}$
. Suppose
$\mathfrak {a}\mathfrak {b}^{-1}=\mathfrak {c}$
. Suppose
![]() $\mathfrak {a}\subseteq \mathfrak {o}$
and
$\mathfrak {a}\subseteq \mathfrak {o}$
and
![]() $(\mathfrak {a},Np)=1$
. Then the natural inclusion
$(\mathfrak {a},Np)=1$
. Then the natural inclusion
![]() $\mathfrak {o}\subseteq \mathfrak {a}^{-1}$
induces isomorphisms
$\mathfrak {o}\subseteq \mathfrak {a}^{-1}$
induces isomorphisms
 $$ \begin{align*} \phi_{\mathfrak{a},\mathfrak{b}}: \mathfrak{a}^{-1}/N\mathfrak{a}^{-1} \simeq \mathfrak{o}/N\mathfrak{o},\qquad \phi^{\prime}_{\mathfrak{a},\mathfrak{b}}: \mathfrak{a}^{-1}/p^{n} \mathfrak{a}^{-1} \simeq \mathfrak{o}/p^{n}\mathfrak{o}. \end{align*} $$
$$ \begin{align*} \phi_{\mathfrak{a},\mathfrak{b}}: \mathfrak{a}^{-1}/N\mathfrak{a}^{-1} \simeq \mathfrak{o}/N\mathfrak{o},\qquad \phi^{\prime}_{\mathfrak{a},\mathfrak{b}}: \mathfrak{a}^{-1}/p^{n} \mathfrak{a}^{-1} \simeq \mathfrak{o}/p^{n}\mathfrak{o}. \end{align*} $$
Consider the unramified cusp
![]() $\left (\mathfrak {a},\mathfrak {b},\phi _{\mathfrak {a},\mathfrak {b}}\right )$
of
$\left (\mathfrak {a},\mathfrak {b},\phi _{\mathfrak {a},\mathfrak {b}}\right )$
of
![]() $M(\mu _{N},\mathfrak {c})$
. Take
$M(\mu _{N},\mathfrak {c})$
. Take
![]() $\mathscr {C}\in \mathrm {Dec}(\mathfrak {a},\mathfrak {b})$
and
$\mathscr {C}\in \mathrm {Dec}(\mathfrak {a},\mathfrak {b})$
and
![]() $\sigma \in \mathscr {C}$
as before. By the construction of the Tate object, the map
$\sigma \in \mathscr {C}$
as before. By the construction of the Tate object, the map
 $\phi ^{\prime }_{\mathfrak {a},\mathfrak {b}}$
yields a natural immersion
$\phi ^{\prime }_{\mathfrak {a},\mathfrak {b}}$
yields a natural immersion
 $\mathcal {D}_{F}^{-1}\otimes \mu _{p^{n}}\to \mathrm {Tate}_{\mathfrak {a},\mathfrak {b}}(q)$
over
$\mathcal {D}_{F}^{-1}\otimes \mu _{p^{n}}\to \mathrm {Tate}_{\mathfrak {a},\mathfrak {b}}(q)$
over
![]() $\bar {S}_{\sigma }$
, which induces an isomorphism
$\bar {S}_{\sigma }$
, which induces an isomorphism
 $$ \begin{align*} \omega_{\mathrm{Tate}_{\mathfrak{a},\mathfrak{b}}(q)}\otimes_{\mathcal{O}_{K}}\mathcal{O}_{K,n}\simeq \omega_{\mathcal{D}_{F}^{-1}\otimes \mu_{p^{n}}}. \end{align*} $$
$$ \begin{align*} \omega_{\mathrm{Tate}_{\mathfrak{a},\mathfrak{b}}(q)}\otimes_{\mathcal{O}_{K}}\mathcal{O}_{K,n}\simeq \omega_{\mathcal{D}_{F}^{-1}\otimes \mu_{p^{n}}}. \end{align*} $$
Note that the map
 $\mathrm {Tr}_{F/\mathbb {Q}}\otimes 1: \mathcal {D}_{F}^{-1}\otimes \mathbb {G}_{\mathrm {m}}\to \mathbb {G}_{\mathrm {m}}$
gives an element
$\mathrm {Tr}_{F/\mathbb {Q}}\otimes 1: \mathcal {D}_{F}^{-1}\otimes \mathbb {G}_{\mathrm {m}}\to \mathbb {G}_{\mathrm {m}}$
gives an element
 $\left (\mathrm {Tr}_{F/\mathbb {Q}}\otimes 1\right )^{*}\frac {dT}{T}$
of the
$\left (\mathrm {Tr}_{F/\mathbb {Q}}\otimes 1\right )^{*}\frac {dT}{T}$
of the
 $\mathcal {O}_{F}\otimes \mathcal {O}\left (\bar {S}_{\sigma }\right )$
-module
$\mathcal {O}_{F}\otimes \mathcal {O}\left (\bar {S}_{\sigma }\right )$
-module
![]() $\omega _{\mathcal {D}_{F}^{-1}\otimes \mathbb {G}_{\mathrm {m}}}\simeq \omega _{\mathrm {Tate}_{\mathfrak {a},\mathfrak {b}}(q)}$
. By the pullback, we obtain a Tate object over
$\omega _{\mathcal {D}_{F}^{-1}\otimes \mathbb {G}_{\mathrm {m}}}\simeq \omega _{\mathrm {Tate}_{\mathfrak {a},\mathfrak {b}}(q)}$
. By the pullback, we obtain a Tate object over
 $\mathrm {Spec}\left (\breve {R}_{\sigma }\right )$
with a canonical invariant differential form which are compatible with those over
$\mathrm {Spec}\left (\breve {R}_{\sigma }\right )$
with a canonical invariant differential form which are compatible with those over
 $\mathrm {Spec}\left (\breve {R}_{\tau }\right )$
for any
$\mathrm {Spec}\left (\breve {R}_{\tau }\right )$
for any
![]() $\tau \in \mathscr {C}$
satisfying
$\tau \in \mathscr {C}$
satisfying
![]() $\tau \subseteq \bar {\sigma }$
.
$\tau \subseteq \bar {\sigma }$
.
We denote the p-adic completion of
![]() $\bar {S}_{\sigma }$
by
$\bar {S}_{\sigma }$
by
![]() $\tilde {S}_{\sigma }$
. We have
$\tilde {S}_{\sigma }$
. We have
 $\tilde {S}_{\sigma }=\mathrm {Spf}\left (\breve {R}_{\sigma }\right )$
, where we consider the p-adic topology on
$\tilde {S}_{\sigma }=\mathrm {Spf}\left (\breve {R}_{\sigma }\right )$
, where we consider the p-adic topology on
![]() $\breve {R}_{\sigma }$
. Its base extension to
$\breve {R}_{\sigma }$
. Its base extension to
![]() $\mathcal {O}_{\mathbb {C}_{p}}$
is denoted by
$\mathcal {O}_{\mathbb {C}_{p}}$
is denoted by
 $\tilde {S}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}=\mathrm {Spf}\left (\tilde {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}\right )$
. Here the affine algebra
$\tilde {S}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}=\mathrm {Spf}\left (\tilde {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}\right )$
. Here the affine algebra
 $ \tilde {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
is the p-adic completion of the ring
$ \tilde {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
is the p-adic completion of the ring
 $\breve {R}_{\sigma }\otimes _{\mathcal {O}_{K}} \mathcal {O}_{\mathbb {C}_{p}}$
.
$\breve {R}_{\sigma }\otimes _{\mathcal {O}_{K}} \mathcal {O}_{\mathbb {C}_{p}}$
.
The identity map
![]() $\breve {R}_{\sigma }\to \breve {R}_{\sigma }$
is continuous if we consider the p-adic topology on the source and the
$\breve {R}_{\sigma }\to \breve {R}_{\sigma }$
is continuous if we consider the p-adic topology on the source and the
 $\left (p,\hat {I}_{\sigma }\right )$
-adic topology on the target. Then, for the case of
$\left (p,\hat {I}_{\sigma }\right )$
-adic topology on the target. Then, for the case of
![]() $\mathscr {C}=\mathscr {C}(\mathfrak {a},\mathfrak {b})$
, its composite with the p-adic completion of the map
$\mathscr {C}=\mathscr {C}(\mathfrak {a},\mathfrak {b})$
, its composite with the p-adic completion of the map
![]() $\bar {S}_{\sigma }\to \bar {M}(\mu _{N},\mathfrak {c})$
gives a morphism of formal schemes
$\bar {S}_{\sigma }\to \bar {M}(\mu _{N},\mathfrak {c})$
gives a morphism of formal schemes
 $\breve {S}_{\sigma } \to \tilde {S}_{\sigma }\to \bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)$
, and also a morphism
$\breve {S}_{\sigma } \to \tilde {S}_{\sigma }\to \bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)$
, and also a morphism
 $\breve {S}_{\mathscr {C}} \to \bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)$
by gluing. Since
$\breve {S}_{\mathscr {C}} \to \bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)$
by gluing. Since
![]() $\breve {R}_{\sigma }$
is Noetherian, the moduli interpretation of
$\breve {R}_{\sigma }$
is Noetherian, the moduli interpretation of
 $\mathfrak {IW}_{w,\mathfrak {c}}^{+}(0)$
as in §3.3.1 is also valid for
$\mathfrak {IW}_{w,\mathfrak {c}}^{+}(0)$
as in §3.3.1 is also valid for
![]() $\breve {R}_{\sigma }$
. We have a commutative diagram
$\breve {R}_{\sigma }$
. We have a commutative diagram

where the top horizontal arrow is the natural inclusion and the other horizontal arrows are induced by the map
![]() $\mathrm {Tr}_{F/\mathbb {Q}}\otimes 1$
. Thus the moduli interpretation and the base extension give a morphism of formal schemes over
$\mathrm {Tr}_{F/\mathbb {Q}}\otimes 1$
. Thus the moduli interpretation and the base extension give a morphism of formal schemes over
 $\mathrm {Spf}\left (\mathcal {O}_{\mathbb {C}_{p}}\right )$
,
$\mathrm {Spf}\left (\mathcal {O}_{\mathbb {C}_{p}}\right )$
,
 $$ \begin{align*} \tau_{\mathfrak{a},\mathfrak{b}}: \breve{S}_{\sigma,\mathcal{O}_{\mathbb{C}_{p}}}\to \tilde{S}_{\sigma,\mathcal{O}_{\mathbb{C}_{p}}} \to \mathfrak{IW}_{w,\mathfrak{c}}^{+}(0)_{\mathcal{O}_{\mathbb{C}_{p}}}. \end{align*} $$
$$ \begin{align*} \tau_{\mathfrak{a},\mathfrak{b}}: \breve{S}_{\sigma,\mathcal{O}_{\mathbb{C}_{p}}}\to \tilde{S}_{\sigma,\mathcal{O}_{\mathbb{C}_{p}}} \to \mathfrak{IW}_{w,\mathfrak{c}}^{+}(0)_{\mathcal{O}_{\mathbb{C}_{p}}}. \end{align*} $$
By gluing, this defines a morphism
 $\breve {S}_{\mathscr {C},\mathcal {O}_{\mathbb {C}_{p}}}\to \mathfrak {IW}^{+}_{w,\mathfrak {c}}(0)_{\mathcal {O}_{\mathbb {C}_{p}}}$
, which we also denote by
$\breve {S}_{\mathscr {C},\mathcal {O}_{\mathbb {C}_{p}}}\to \mathfrak {IW}^{+}_{w,\mathfrak {c}}(0)_{\mathcal {O}_{\mathbb {C}_{p}}}$
, which we also denote by
![]() $\tau _{\mathfrak {a},\mathfrak {b}}$
.
$\tau _{\mathfrak {a},\mathfrak {b}}$
.
Lemma 4.2. The natural map
 $\tilde {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}} \to \breve {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
is injective. In particular, the ring
$\tilde {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}} \to \breve {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
is injective. In particular, the ring
 $\tilde {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
is an integral domain.
$\tilde {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
is an integral domain.
Proof. We have an isomorphism
 $$ \begin{align} \tilde{R}_{\sigma,\mathcal{O}_{\mathbb{C}_{p}}}\simeq \varprojlim_{n} \varinjlim_{L/K} \mathcal{O}_{L,n}\left[X_{\leq r}, X_{>r}^{\pm}\right][[Z]]/(Z-X_{1}\dotsm X_{r}), \end{align} $$
$$ \begin{align} \tilde{R}_{\sigma,\mathcal{O}_{\mathbb{C}_{p}}}\simeq \varprojlim_{n} \varinjlim_{L/K} \mathcal{O}_{L,n}\left[X_{\leq r}, X_{>r}^{\pm}\right][[Z]]/(Z-X_{1}\dotsm X_{r}), \end{align} $$
where the direct limit is taken with respect to the directed set of finite extensions
![]() $L/K$
in
$L/K$
in
![]() $\bar {\mathbb {Q}}_{p}$
. Since the map
$\bar {\mathbb {Q}}_{p}$
. Since the map
 $$ \begin{align*} \mathcal{O}_{L,n}\left[X_{\leq r}, X_{>r}^{\pm}\right]/(X_{1}\dotsm X_{r})^{m} \to \mathcal{O}_{\mathbb{C}_{p},n}\left[X_{\leq r}, X_{>r}^{\pm}\right]/(X_{1}\dotsm X_{r})^{m} \end{align*} $$
$$ \begin{align*} \mathcal{O}_{L,n}\left[X_{\leq r}, X_{>r}^{\pm}\right]/(X_{1}\dotsm X_{r})^{m} \to \mathcal{O}_{\mathbb{C}_{p},n}\left[X_{\leq r}, X_{>r}^{\pm}\right]/(X_{1}\dotsm X_{r})^{m} \end{align*} $$
is injective for any such
![]() $L/K$
, the injectivity of the lemma follows from expression (4.6). Lemma 4.1 yields the last assertion.
$L/K$
, the injectivity of the lemma follows from expression (4.6). Lemma 4.1 yields the last assertion.
For any finite extension
![]() $L/K$
, we write the p-adic completion
$L/K$
, we write the p-adic completion
 $$ \begin{align*} \breve{R}_{\sigma} \hat{\otimes}_{\mathcal{O}_{K}} \mathcal{O}_{L}=\mathcal{O}_{L}\left\langle X_{\leq r}, X_{>r}^{\pm}\right\rangle [[Z]]/(Z-X_{1}\dotsm X_{r}) \end{align*} $$
$$ \begin{align*} \breve{R}_{\sigma} \hat{\otimes}_{\mathcal{O}_{K}} \mathcal{O}_{L}=\mathcal{O}_{L}\left\langle X_{\leq r}, X_{>r}^{\pm}\right\rangle [[Z]]/(Z-X_{1}\dotsm X_{r}) \end{align*} $$
also as
![]() $\tilde {R}_{\mathcal {O}_{L}}$
. Let
$\tilde {R}_{\mathcal {O}_{L}}$
. Let
![]() $\pi _{L}$
be a uniformizer of L. By Lemma 4.1, the ring
$\pi _{L}$
be a uniformizer of L. By Lemma 4.1, the ring
![]() $\tilde {R}_{\mathcal {O}_{L}}/(\pi _{L})$
is an integral domain. Since
$\tilde {R}_{\mathcal {O}_{L}}/(\pi _{L})$
is an integral domain. Since
![]() $\tilde {R}_{\mathcal {O}_{L}}$
is normal, the localization
$\tilde {R}_{\mathcal {O}_{L}}$
is normal, the localization
 $\left (\tilde {R}_{\mathcal {O}_{L}}\right )_{\left (\pi _{L}\right )}$
is a discrete valuation ring with uniformizer
$\left (\tilde {R}_{\mathcal {O}_{L}}\right )_{\left (\pi _{L}\right )}$
is a discrete valuation ring with uniformizer
![]() $\pi _{L}$
such that Z is invertible. Put
$\pi _{L}$
such that Z is invertible. Put
 $\tilde {R}_{\infty }=\varinjlim _{L/K} \tilde {R}_{\mathcal {O}_{L}}$
and
$\tilde {R}_{\infty }=\varinjlim _{L/K} \tilde {R}_{\mathcal {O}_{L}}$
and
 $m_{\infty }=\varinjlim _{L/K} (\pi _{L})$
, where the direct limits are taken as before. Then the localization
$m_{\infty }=\varinjlim _{L/K} (\pi _{L})$
, where the direct limits are taken as before. Then the localization
 $\left (\tilde {R}_{\infty }\right )_{m_{\infty }}=\varinjlim _{L/K} \left (\tilde {R}_{\mathcal {O}_{L}}\right )_{\left (\pi _{L}\right )}$
is a valuation ring. Let
$\left (\tilde {R}_{\infty }\right )_{m_{\infty }}=\varinjlim _{L/K} \left (\tilde {R}_{\mathcal {O}_{L}}\right )_{\left (\pi _{L}\right )}$
is a valuation ring. Let
![]() $\mathcal {O}_{\mathcal {K}_{\sigma }}$
be its p-adic completion. By formula (4.9), the ring
$\mathcal {O}_{\mathcal {K}_{\sigma }}$
be its p-adic completion. By formula (4.9), the ring
 $\tilde {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
coincides with the p-adic completion of
$\tilde {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
coincides with the p-adic completion of
![]() $\tilde {R}_{\infty }$
. Since the p-adic topology on
$\tilde {R}_{\infty }$
. Since the p-adic topology on
![]() $\tilde {R}_{\infty }$
is induced by that on
$\tilde {R}_{\infty }$
is induced by that on
 $\left (\tilde {R}_{\infty }\right )_{m_{\infty }}$
, we obtain an injection
$\left (\tilde {R}_{\infty }\right )_{m_{\infty }}$
, we obtain an injection
 $\tilde {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}\to \mathcal {O}_{\mathcal {K}_{\sigma }}$
. This defines a morphism of p-adic formal schemes
$\tilde {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}\to \mathcal {O}_{\mathcal {K}_{\sigma }}$
. This defines a morphism of p-adic formal schemes
 $\mathrm {Spf}\left (\mathcal {O}_{\mathcal {K}_{\sigma }}\right )\to \tilde {S}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
for any
$\mathrm {Spf}\left (\mathcal {O}_{\mathcal {K}_{\sigma }}\right )\to \tilde {S}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
for any
![]() $\sigma \in \mathscr {C}(\mathfrak {a},\mathfrak {b})$
. In particular, we have the pullback of
$\sigma \in \mathscr {C}(\mathfrak {a},\mathfrak {b})$
. In particular, we have the pullback of
![]() $\mathrm {Tate}_{\mathfrak {a},\mathfrak {b}}(q)$
over
$\mathrm {Tate}_{\mathfrak {a},\mathfrak {b}}(q)$
over
![]() $\mathrm {Spec}\left (\mathcal {O}_{\mathcal {K}_{\sigma }}\right )$
which is an HBAV. Since
$\mathrm {Spec}\left (\mathcal {O}_{\mathcal {K}_{\sigma }}\right )$
which is an HBAV. Since
![]() $\mathcal {O}_{\mathcal {K}_{\sigma }}$
is quasi-idyllic, we have the moduli interpretation of any morphism
$\mathcal {O}_{\mathcal {K}_{\sigma }}$
is quasi-idyllic, we have the moduli interpretation of any morphism
 $\mathrm {Spf}\left (\mathcal {O}_{\mathcal {K}_{\sigma }}\right ) \to \mathfrak {IW}^{+}_{w,\mathfrak {c}}(0)_{\mathcal {O}_{\mathbb {C}_{p}}}$
over
$\mathrm {Spf}\left (\mathcal {O}_{\mathcal {K}_{\sigma }}\right ) \to \mathfrak {IW}^{+}_{w,\mathfrak {c}}(0)_{\mathcal {O}_{\mathbb {C}_{p}}}$
over
 $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)_{\mathcal {O}_{\mathbb {C}_{p}}}$
as in §3.3.1. The additional structures of the Tate object over
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)_{\mathcal {O}_{\mathbb {C}_{p}}}$
as in §3.3.1. The additional structures of the Tate object over
 $\mathrm {Spec}\left (\breve {R}_{\sigma }\right )$
define a canonical test object
$\mathrm {Spec}\left (\breve {R}_{\sigma }\right )$
define a canonical test object
over
![]() $\mathrm {Spec}\left (\mathcal {O}_{\mathcal {K}_{\sigma }}\right )$
. This corresponds via the moduli interpretation to a map
$\mathrm {Spec}\left (\mathcal {O}_{\mathcal {K}_{\sigma }}\right )$
. This corresponds via the moduli interpretation to a map
 $$ \begin{align*} \tau_{\mathfrak{a},\mathfrak{b},\mathcal{O}_{\mathcal{K}_{\sigma}}}: \mathrm{Spf}\left(\mathcal{O}_{\mathcal{K}_{\sigma}}\right)\to \mathfrak{IW}_{w,\mathfrak{c}}^{+}(0)_{\mathcal{O}_{\mathbb{C}_{p}}} \end{align*} $$
$$ \begin{align*} \tau_{\mathfrak{a},\mathfrak{b},\mathcal{O}_{\mathcal{K}_{\sigma}}}: \mathrm{Spf}\left(\mathcal{O}_{\mathcal{K}_{\sigma}}\right)\to \mathfrak{IW}_{w,\mathfrak{c}}^{+}(0)_{\mathcal{O}_{\mathbb{C}_{p}}} \end{align*} $$
satisfying the following property: the composite
 $\breve {S}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}\to \breve {S}_{\mathscr {C},\mathcal {O}_{\mathbb {C}_{p}}}\overset {\tau _{\mathfrak {a},\mathfrak {b}}}{\to }\mathfrak {IW}_{w,\mathfrak {c}}^{+}(0)_{\mathcal {O}_{\mathbb {C}_{p}}}$
factors through
$\breve {S}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}\to \breve {S}_{\mathscr {C},\mathcal {O}_{\mathbb {C}_{p}}}\overset {\tau _{\mathfrak {a},\mathfrak {b}}}{\to }\mathfrak {IW}_{w,\mathfrak {c}}^{+}(0)_{\mathcal {O}_{\mathbb {C}_{p}}}$
factors through
 $\tilde {S}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
and its restriction to
$\tilde {S}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
and its restriction to
![]() $\mathrm {Spf}\left (\mathcal {O}_{\mathcal {K}_{\sigma }}\right )$
equals
$\mathrm {Spf}\left (\mathcal {O}_{\mathcal {K}_{\sigma }}\right )$
equals
![]() $\tau _{\mathfrak {a},\mathfrak {b},\mathcal {O}_{\mathcal {K}_{\sigma }}}$
, as in the diagram
$\tau _{\mathfrak {a},\mathfrak {b},\mathcal {O}_{\mathcal {K}_{\sigma }}}$
, as in the diagram

Let
![]() $\kappa \in \mathcal {W}\left (\mathbb {C}_{p}\right )$
be any n-analytic weight. Since the formal scheme
$\kappa \in \mathcal {W}\left (\mathbb {C}_{p}\right )$
be any n-analytic weight. Since the formal scheme
 $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(v)_{\mathcal {O}_{\mathbb {C}_{p}}}$
is quasi-compact and the sheaf
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(v)_{\mathcal {O}_{\mathbb {C}_{p}}}$
is quasi-compact and the sheaf
![]() $\mathbf {\Omega }^{\kappa }$
is coherent, we have
$\mathbf {\Omega }^{\kappa }$
is coherent, we have
 $$ \begin{align*} M(\mu_{N},\mathfrak{c},\kappa)(v)=H^{0}\left(\bar{\mathfrak{M}}(\mu_{N},\mathfrak{c})(v)_{\mathcal{O}_{\mathbb{C}_{p}}}, \mathbf{\Omega}^{\kappa}\right)[1/p]\subseteq \mathcal{O}\left(\mathfrak{IW}_{w,\mathfrak{c}}^{+}(v)_{\mathcal{O}_{\mathbb{C}_{p}}}\right)[1/p]. \end{align*} $$
$$ \begin{align*} M(\mu_{N},\mathfrak{c},\kappa)(v)=H^{0}\left(\bar{\mathfrak{M}}(\mu_{N},\mathfrak{c})(v)_{\mathcal{O}_{\mathbb{C}_{p}}}, \mathbf{\Omega}^{\kappa}\right)[1/p]\subseteq \mathcal{O}\left(\mathfrak{IW}_{w,\mathfrak{c}}^{+}(v)_{\mathcal{O}_{\mathbb{C}_{p}}}\right)[1/p]. \end{align*} $$
For any element
![]() $f_{\mathfrak {c}}$
of
$f_{\mathfrak {c}}$
of
![]() $M(\mu _{N},\mathfrak {c},\kappa )(v)$
, we define the q-expansion
$M(\mu _{N},\mathfrak {c},\kappa )(v)$
, we define the q-expansion
![]() $f_{\mathfrak {c}}(q)$
of
$f_{\mathfrak {c}}(q)$
of
![]() $f_{\mathfrak {c}}$
by
$f_{\mathfrak {c}}$
by
 $$ \begin{align*} f_{\mathfrak{c}}(q)=\tau^{*}_{\mathfrak{o},\mathfrak{c}^{-1}}(f_{\mathfrak{c}})\in \mathcal{O}\left(\breve{S}_{\mathscr{C},\mathcal{O}_{\mathbb{C}_{p}}}\right)[1/p]=\mathcal{O}_{\mathbb{C}_{p}}\left[\left[q^{\xi}\mid \xi\in \left(\mathfrak{c}^{-1}\right)^{+}\cup\{0\}\right]\right][1/p]. \end{align*} $$
$$ \begin{align*} f_{\mathfrak{c}}(q)=\tau^{*}_{\mathfrak{o},\mathfrak{c}^{-1}}(f_{\mathfrak{c}})\in \mathcal{O}\left(\breve{S}_{\mathscr{C},\mathcal{O}_{\mathbb{C}_{p}}}\right)[1/p]=\mathcal{O}_{\mathbb{C}_{p}}\left[\left[q^{\xi}\mid \xi\in \left(\mathfrak{c}^{-1}\right)^{+}\cup\{0\}\right]\right][1/p]. \end{align*} $$
Thus, for any
 $f=(f_{\mathfrak {c}})_{\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{\left (p\right )}}$
, we can write
$f=(f_{\mathfrak {c}})_{\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{\left (p\right )}}$
, we can write
 $$ \begin{align*} f_{\mathfrak{c}}(q)=a_{\mathfrak{o},\mathfrak{c}^{-1}}(f,0)+\sum_{\xi\in \left(\mathfrak{c}^{-1}\right)^{+}} a_{\mathfrak{o},\mathfrak{c}^{-1}}(f,\xi)q^{\xi} \end{align*} $$
$$ \begin{align*} f_{\mathfrak{c}}(q)=a_{\mathfrak{o},\mathfrak{c}^{-1}}(f,0)+\sum_{\xi\in \left(\mathfrak{c}^{-1}\right)^{+}} a_{\mathfrak{o},\mathfrak{c}^{-1}}(f,\xi)q^{\xi} \end{align*} $$
with some
![]() $a_{\mathfrak {o},\mathfrak {c}^{-1}}(f,\xi )\in \mathbb {C}_{p}$
. For any refinement
$a_{\mathfrak {o},\mathfrak {c}^{-1}}(f,\xi )\in \mathbb {C}_{p}$
. For any refinement
 $\mathscr {C}^{\prime }\in \mathrm {Dec}\left (\mathfrak {o},\mathfrak {c}^{-1}\right )$
of
$\mathscr {C}^{\prime }\in \mathrm {Dec}\left (\mathfrak {o},\mathfrak {c}^{-1}\right )$
of
![]() $\mathscr {C}$
, the natural map
$\mathscr {C}$
, the natural map
 $\breve {S}_{\mathscr {C}^{\prime },\mathcal {O}_{\mathbb {C}_{p}}}\to \breve {S}_{\mathscr {C},\mathcal {O}_{\mathbb {C}_{p}}}$
induces the identity map on the ring
$\breve {S}_{\mathscr {C}^{\prime },\mathcal {O}_{\mathbb {C}_{p}}}\to \breve {S}_{\mathscr {C},\mathcal {O}_{\mathbb {C}_{p}}}$
induces the identity map on the ring
 $\mathcal {O}_{\mathbb {C}_{p}}\left [\left [q^{\xi }\mid \xi \in \left (\mathfrak {c}^{-1}\right )^{+}\cup \{0\}\right ]\right ][1/p]$
. Thus we can compute the q-expansion by taking any refinement of the fixed cone decomposition
$\mathcal {O}_{\mathbb {C}_{p}}\left [\left [q^{\xi }\mid \xi \in \left (\mathfrak {c}^{-1}\right )^{+}\cup \{0\}\right ]\right ][1/p]$
. Thus we can compute the q-expansion by taking any refinement of the fixed cone decomposition
 $\mathscr {C}\left (\mathfrak {o},\mathfrak {c}^{-1}\right )$
in
$\mathscr {C}\left (\mathfrak {o},\mathfrak {c}^{-1}\right )$
in
 $\mathrm {Dec}\left (\mathfrak {o},\mathfrak {c}^{-1}\right )$
. We say that an eigenform f is normalized if
$\mathrm {Dec}\left (\mathfrak {o},\mathfrak {c}^{-1}\right )$
. We say that an eigenform f is normalized if
![]() $a_{\mathfrak {o},\mathfrak {o}}(f,1)=1$
.
$a_{\mathfrak {o},\mathfrak {o}}(f,1)=1$
.
By presentations (4.2) and (4.5), we have an isomorphism
 $$ \begin{align*} \left(\breve{R}_{\sigma}/\hat{I}_{\sigma} \breve{R}_{\sigma}\right)\hat{\otimes}_{\mathcal{O}_{K}}\mathcal{O}_{\mathbb{C}_{p}}\simeq \breve{R}_{\sigma,\mathcal{O}_{\mathbb{C}_{p}}}/\hat{I}_{\sigma} \breve{R}_{\sigma, \mathcal{O}_{\mathbb{C}_{p}}}, \end{align*} $$
$$ \begin{align*} \left(\breve{R}_{\sigma}/\hat{I}_{\sigma} \breve{R}_{\sigma}\right)\hat{\otimes}_{\mathcal{O}_{K}}\mathcal{O}_{\mathbb{C}_{p}}\simeq \breve{R}_{\sigma,\mathcal{O}_{\mathbb{C}_{p}}}/\hat{I}_{\sigma} \breve{R}_{\sigma, \mathcal{O}_{\mathbb{C}_{p}}}, \end{align*} $$
which implies
![]() $a_{\mathfrak {o},\mathfrak {c}^{-1}}(f,0)=0$
if
$a_{\mathfrak {o},\mathfrak {c}^{-1}}(f,0)=0$
if
![]() $f_{\mathfrak {c}}\in S(\mu _{N},\mathfrak {c},\kappa )(v)$
.
$f_{\mathfrak {c}}\in S(\mu _{N},\mathfrak {c},\kappa )(v)$
.
4.2 Weak multiplicity one theorem
Let
![]() $(\nu ,w)\in \mathcal {W}^{G}\left (\mathbb {C}_{p}\right )$
be an n-analytic weight. Let
$(\nu ,w)\in \mathcal {W}^{G}\left (\mathbb {C}_{p}\right )$
be an n-analytic weight. Let
 $f=(f_{\mathfrak {c}})_{\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{\left (p\right )}}$
be a nonzero eigenform in
$f=(f_{\mathfrak {c}})_{\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{\left (p\right )}}$
be a nonzero eigenform in
![]() $S^{G}(\mu _{N}, (\nu ,w))(v)$
. For any nonzero ideal
$S^{G}(\mu _{N}, (\nu ,w))(v)$
. For any nonzero ideal
![]() $\mathfrak {n}\subseteq \mathfrak {o}$
, let
$\mathfrak {n}\subseteq \mathfrak {o}$
, let
![]() $\Lambda (\mathfrak {n})$
be the eigenvalue of
$\Lambda (\mathfrak {n})$
be the eigenvalue of
![]() $T_{\mathfrak {n}}$
acting on f. We set
$T_{\mathfrak {n}}$
acting on f. We set
![]() $\Phi (\mathfrak {n})$
to be the eigenvalue of
$\Phi (\mathfrak {n})$
to be the eigenvalue of
![]() $S_{\mathfrak {n}}$
for
$S_{\mathfrak {n}}$
for
![]() $(\mathfrak {n},Np)=1$
and
$(\mathfrak {n},Np)=1$
and
![]() ${\Phi (\mathfrak {n})=}0$
otherwise. We put
${\Phi (\mathfrak {n})=}0$
otherwise. We put
 $\mu _{\mathfrak {n}}=\left (\mathcal {D}_{F}^{-1}\otimes \mathbb {G}_{\mathrm {m}}\right )[\mathfrak {n}]$
. Any element
$\mu _{\mathfrak {n}}=\left (\mathcal {D}_{F}^{-1}\otimes \mathbb {G}_{\mathrm {m}}\right )[\mathfrak {n}]$
. Any element
![]() $\zeta $
of
$\zeta $
of
 $\mu _{\mathfrak {n}}(L)\subseteq \left (\mathcal {D}^{-1}_{F}\otimes \mathbb {G}_{\mathrm {m}}\right )(L)$
with some extension
$\mu _{\mathfrak {n}}(L)\subseteq \left (\mathcal {D}^{-1}_{F}\otimes \mathbb {G}_{\mathrm {m}}\right )(L)$
with some extension
![]() $L/K$
defines a ring homomorphism
$L/K$
defines a ring homomorphism
 $\zeta : \mathcal {O}\left (\mathcal {D}^{-1}_{F}\otimes \mathbb {G}_{\mathrm {m}}\right )\to L$
. We put
$\zeta : \mathcal {O}\left (\mathcal {D}^{-1}_{F}\otimes \mathbb {G}_{\mathrm {m}}\right )\to L$
. We put
![]() $\zeta ^{\eta }=\zeta (\mathfrak {X}^{\eta })$
for any
$\zeta ^{\eta }=\zeta (\mathfrak {X}^{\eta })$
for any
![]() $\eta \in \mathfrak {o}$
, which gives a homomorphism
$\eta \in \mathfrak {o}$
, which gives a homomorphism
![]() $\mathfrak {o}/\mathfrak {n}\to L^{\times }$
. We fix an element
$\mathfrak {o}/\mathfrak {n}\to L^{\times }$
. We fix an element
 $\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
.
$\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
.
4.2.1 q-Expansion and Hecke operators
For any
![]() $\mathscr {C}\in \mathrm {Dec}(\mathfrak {a},\mathfrak {b})$
and any maximal ideal
$\mathscr {C}\in \mathrm {Dec}(\mathfrak {a},\mathfrak {b})$
and any maximal ideal
![]() $\mathfrak {m}$
of
$\mathfrak {m}$
of
![]() $\mathfrak {o}$
, we can find
$\mathfrak {o}$
, we can find
 $\mathscr {C}^{\prime }\in \mathrm {Dec}\left (\mathfrak {a},\mathfrak {m}^{-1}\mathfrak {b}\right )$
which is a refinement of
$\mathscr {C}^{\prime }\in \mathrm {Dec}\left (\mathfrak {a},\mathfrak {m}^{-1}\mathfrak {b}\right )$
which is a refinement of
![]() $\mathscr {C}$
. For any
$\mathscr {C}$
. For any
![]() $\sigma \in \mathscr {C}$
and
$\sigma \in \mathscr {C}$
and
![]() $\tau \in \mathscr {C}^{\prime }$
satisfying
$\tau \in \mathscr {C}^{\prime }$
satisfying
![]() $\sigma \supseteq \tau $
, we have natural maps
$\sigma \supseteq \tau $
, we have natural maps
![]() $\hat {R}_{\sigma }\to \hat {R}_{\tau }$
,
$\hat {R}_{\sigma }\to \hat {R}_{\tau }$
,
 $\hat {R}_{\sigma }^{0}\to \hat {R}_{\tau }^{0}$
, and
$\hat {R}_{\sigma }^{0}\to \hat {R}_{\tau }^{0}$
, and
![]() $\breve {R}_{\sigma }\to \breve {R}_{\tau }$
. Consider the case
$\breve {R}_{\sigma }\to \breve {R}_{\tau }$
. Consider the case
![]() $\mathfrak {a}=\mathfrak {o}$
. Let
$\mathfrak {a}=\mathfrak {o}$
. Let
![]() $\zeta $
be an element of
$\zeta $
be an element of
![]() $\mu _{\mathfrak {m}}(K)$
. Fix an isomorphism of
$\mu _{\mathfrak {m}}(K)$
. Fix an isomorphism of
![]() $\mathfrak {o}$
-modules
$\mathfrak {o}$
-modules
Then we have a natural ring homomorphism
We denote by
![]() $\mathrm {Tate}_{\mathfrak {o},\mathfrak {m}^{-1}\mathfrak {b}}(q\zeta ^{\rho })$
the pullback of
$\mathrm {Tate}_{\mathfrak {o},\mathfrak {m}^{-1}\mathfrak {b}}(q\zeta ^{\rho })$
the pullback of
![]() $\mathrm {Tate}_{\mathfrak {o},\mathfrak {m}^{-1}\mathfrak {b}}(q)$
by this map.
$\mathrm {Tate}_{\mathfrak {o},\mathfrak {m}^{-1}\mathfrak {b}}(q)$
by this map.
On the other hand, we have
![]() $\mathrm {Dec}(\mathfrak {a},\mathfrak {b})=\mathrm {Dec}(\mathfrak {a},\eta \mathfrak {b})$
for any unramified cusp
$\mathrm {Dec}(\mathfrak {a},\mathfrak {b})=\mathrm {Dec}(\mathfrak {a},\eta \mathfrak {b})$
for any unramified cusp
![]() $(\mathfrak {a},\mathfrak {b},\phi )$
and
$(\mathfrak {a},\mathfrak {b},\phi )$
and
![]() $\eta \in F^{\times ,+}$
. Thus any
$\eta \in F^{\times ,+}$
. Thus any
![]() $\sigma \in \mathscr {C}$
gives similar rings to
$\sigma \in \mathscr {C}$
gives similar rings to
![]() $\hat {R}_{\sigma }$
,
$\hat {R}_{\sigma }$
,
![]() $\hat {R}_{\sigma }^{0}$
, and
$\hat {R}_{\sigma }^{0}$
, and
![]() $\breve {R}_{\sigma }$
for the cusp
$\breve {R}_{\sigma }$
for the cusp
![]() $(\mathfrak {a},\eta \mathfrak {b}, \phi )$
, which are denoted by
$(\mathfrak {a},\eta \mathfrak {b}, \phi )$
, which are denoted by
 $\hat {R}_{\eta , \sigma }$
,
$\hat {R}_{\eta , \sigma }$
,
 $\hat {R}_{\eta ,\sigma }^{0}$
, and
$\hat {R}_{\eta ,\sigma }^{0}$
, and
 $\breve {R}_{\eta ,\sigma }$
, respectively. We have a natural ring homomorphism
$\breve {R}_{\eta ,\sigma }$
, respectively. We have a natural ring homomorphism
 $$ \begin{align*} q^{\eta}: \hat{R}_{\sigma} \to \hat{R}_{\eta,\sigma},\quad q^{\xi}\mapsto q^{\xi\eta}. \end{align*} $$
$$ \begin{align*} q^{\eta}: \hat{R}_{\sigma} \to \hat{R}_{\eta,\sigma},\quad q^{\xi}\mapsto q^{\xi\eta}. \end{align*} $$
We denote by
![]() $\mathrm {Tate}_{\mathfrak {a},\mathfrak {b}}(q^{\eta })$
the pullback of
$\mathrm {Tate}_{\mathfrak {a},\mathfrak {b}}(q^{\eta })$
the pullback of
![]() $\mathrm {Tate}_{\mathfrak {a},\mathfrak {b}}(q)$
by this map.
$\mathrm {Tate}_{\mathfrak {a},\mathfrak {b}}(q)$
by this map.
We will omit entries of test objects
![]() $(A,\iota ,\lambda ,\psi ,u,\alpha )$
for overconvergent Hilbert modular forms if they are clear from the context.
$(A,\iota ,\lambda ,\psi ,u,\alpha )$
for overconvergent Hilbert modular forms if they are clear from the context.
Lemma 4.3. We have an isomorphism of test objects over
 $\hat {R}_{\eta ,\sigma }^{0}$
$\hat {R}_{\eta ,\sigma }^{0}$
 $$ \begin{align*} \left(\mathrm{Tate}_{\mathfrak{o},\eta\mathfrak{c}^{-1}}(q),\lambda_{\mathfrak{o},\eta\mathfrak{c}^{-1}}\right)\simeq \left(\mathrm{Tate}_{\mathfrak{o},\mathfrak{c}^{-1}}(q^{\eta}),\eta\lambda_{\mathfrak{o},\mathfrak{c}^{-1}}\right). \end{align*} $$
$$ \begin{align*} \left(\mathrm{Tate}_{\mathfrak{o},\eta\mathfrak{c}^{-1}}(q),\lambda_{\mathfrak{o},\eta\mathfrak{c}^{-1}}\right)\simeq \left(\mathrm{Tate}_{\mathfrak{o},\mathfrak{c}^{-1}}(q^{\eta}),\eta\lambda_{\mathfrak{o},\mathfrak{c}^{-1}}\right). \end{align*} $$
Proof. We denote by
![]() $\rvert _{q^{\eta }}$
the pullback along the map
$\rvert _{q^{\eta }}$
the pullback along the map
![]() $q^{\eta }$
. Consider the composite
$q^{\eta }$
. Consider the composite
 $$ \begin{align*} \mathfrak{c}^{-1} \to \mathcal{D}_{F}^{-1}\otimes \mathbb{G}_{\mathrm{m}}\left(\hat{R}_{\sigma}^{0}\right)\to \mathcal{D}_{F}^{-1}\otimes \mathbb{G}_{\mathrm{m}}\rvert_{q^{\eta}}\left(\hat{R}_{\eta,\sigma}^{0}\right) \end{align*} $$
$$ \begin{align*} \mathfrak{c}^{-1} \to \mathcal{D}_{F}^{-1}\otimes \mathbb{G}_{\mathrm{m}}\left(\hat{R}_{\sigma}^{0}\right)\to \mathcal{D}_{F}^{-1}\otimes \mathbb{G}_{\mathrm{m}}\rvert_{q^{\eta}}\left(\hat{R}_{\eta,\sigma}^{0}\right) \end{align*} $$
of the map
 $\alpha \mapsto \left (\mathfrak {X}^{\xi }\mapsto q^{\alpha \xi }\ (\xi \in \mathfrak {o})\right )$
and the map
$\alpha \mapsto \left (\mathfrak {X}^{\xi }\mapsto q^{\alpha \xi }\ (\xi \in \mathfrak {o})\right )$
and the map
![]() $q^{\eta }$
, which we also denote by
$q^{\eta }$
, which we also denote by
![]() $q^{\eta }$
. We also have a similar map
$q^{\eta }$
. We also have a similar map
 $q^{\eta }: \eta \mathfrak {c}^{-1}\to \eta \mathcal {D}_{F}^{-1}\otimes \mathbb {G}_{\mathrm {m}}\rvert _{q^{\eta }}\left (\hat {R}_{\eta ,\sigma }^{0}\right )$
. Then the following diagram over
$q^{\eta }: \eta \mathfrak {c}^{-1}\to \eta \mathcal {D}_{F}^{-1}\otimes \mathbb {G}_{\mathrm {m}}\rvert _{q^{\eta }}\left (\hat {R}_{\eta ,\sigma }^{0}\right )$
. Then the following diagram over
 $\hat {R}_{\eta ,\sigma }^{0}$
is commutative:
$\hat {R}_{\eta ,\sigma }^{0}$
is commutative:

This yields an isomorphism
![]() $\mathrm {Tate}_{\mathfrak {o},\eta \mathfrak {c}^{-1}}(q)\to \mathrm {Tate}_{\mathfrak {o},\mathfrak {c}^{-1}}(q^{\eta })$
, as in the lemma.
$\mathrm {Tate}_{\mathfrak {o},\eta \mathfrak {c}^{-1}}(q)\to \mathrm {Tate}_{\mathfrak {o},\mathfrak {c}^{-1}}(q^{\eta })$
, as in the lemma.
Lemma 4.4. Let
![]() $\mathfrak {m}$
be a maximal ideal of
$\mathfrak {m}$
be a maximal ideal of
![]() $\mathfrak {o}$
satisfying
$\mathfrak {o}$
satisfying
![]() $\mathfrak {m}\nmid pN$
. Let
$\mathfrak {m}\nmid pN$
. Let
![]() $\mathfrak {c}$
be an element of
$\mathfrak {c}$
be an element of
 $\left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
. Take any elements
$\left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
. Take any elements
![]() $x,y\in F^{\times ,+,(p)}$
such that
$x,y\in F^{\times ,+,(p)}$
such that
![]() $\mathfrak {c}^{\prime }=x\mathfrak {m} \mathfrak {c}$
and
$\mathfrak {c}^{\prime }=x\mathfrak {m} \mathfrak {c}$
and
![]() $\mathfrak {c}^{\prime \prime }=xy^{-1}\mathfrak {m}^{-1}\mathfrak {c}$
are elements of
$\mathfrak {c}^{\prime \prime }=xy^{-1}\mathfrak {m}^{-1}\mathfrak {c}$
are elements of
 $\left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
. Fix an isomorphism of
$\left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
. Fix an isomorphism of
![]() $\mathfrak {o}$
-modules
$\mathfrak {o}$
-modules
![]() $\rho :(x\mathfrak {m}\mathfrak {c})^{-1}/(x\mathfrak {c})^{-1}\simeq \mathfrak {o}/\mathfrak {m}$
. Then we have
$\rho :(x\mathfrak {m}\mathfrak {c})^{-1}/(x\mathfrak {c})^{-1}\simeq \mathfrak {o}/\mathfrak {m}$
. Then we have
 $$ \begin{align*} (T_{\mathfrak{m}} f)_{\mathfrak{c}}(q)=\frac{\nu(x)}{\mathrm{N}_{F/\mathbb{Q}}(\mathfrak{m})}\left(\frac{\mathrm{N}_{F/\mathbb{Q}}(\mathfrak{m})^{2}\Phi(\mathfrak{m})}{\nu(y)} f_{\mathfrak{c}^{\prime\prime}}\left(q^{xy^{-1}}\right)+\sum_{\zeta\in \mu_{\mathfrak{m}}\left(\bar{\mathbb{Q}}_{p}\right)}f_{\mathfrak{c}^{\prime}}(q^{x}\zeta^{\rho})\right). \end{align*} $$
$$ \begin{align*} (T_{\mathfrak{m}} f)_{\mathfrak{c}}(q)=\frac{\nu(x)}{\mathrm{N}_{F/\mathbb{Q}}(\mathfrak{m})}\left(\frac{\mathrm{N}_{F/\mathbb{Q}}(\mathfrak{m})^{2}\Phi(\mathfrak{m})}{\nu(y)} f_{\mathfrak{c}^{\prime\prime}}\left(q^{xy^{-1}}\right)+\sum_{\zeta\in \mu_{\mathfrak{m}}\left(\bar{\mathbb{Q}}_{p}\right)}f_{\mathfrak{c}^{\prime}}(q^{x}\zeta^{\rho})\right). \end{align*} $$
Proof. For any
 $\mathscr {C}\in \mathrm {Dec}\left (\mathfrak {o},\mathfrak {c}^{-1}\right )$
and
$\mathscr {C}\in \mathrm {Dec}\left (\mathfrak {o},\mathfrak {c}^{-1}\right )$
and
 $\mathscr {C}^{\prime }\in \mathrm {Dec}\left (\mathfrak {m}, \mathfrak {c}^{-1}\right )$
, we choose
$\mathscr {C}^{\prime }\in \mathrm {Dec}\left (\mathfrak {m}, \mathfrak {c}^{-1}\right )$
, we choose
 $\mathscr {C}^{\prime \prime }\in \mathrm {Dec}\left (\mathfrak {o}, (\mathfrak {m}\mathfrak {c})^{-1}\right )$
such that
$\mathscr {C}^{\prime \prime }\in \mathrm {Dec}\left (\mathfrak {o}, (\mathfrak {m}\mathfrak {c})^{-1}\right )$
such that
![]() $\mathscr {C}^{\prime \prime }$
is a common refinement of
$\mathscr {C}^{\prime \prime }$
is a common refinement of
![]() $\mathscr {C}$
and
$\mathscr {C}$
and
![]() $\mathscr {C}^{\prime }$
. For any
$\mathscr {C}^{\prime }$
. For any
![]() $\sigma \in \mathscr {C}$
and
$\sigma \in \mathscr {C}$
and
![]() $\sigma ^{\prime }\in \mathscr {C}^{\prime }$
, take
$\sigma ^{\prime }\in \mathscr {C}^{\prime }$
, take
![]() $\tau \in \mathscr {C}^{\prime \prime }$
satisfying
$\tau \in \mathscr {C}^{\prime \prime }$
satisfying
![]() $\tau \subseteq \sigma ,\sigma ^{\prime }$
. By diagram (4.10) and the inclusions
$\tau \subseteq \sigma ,\sigma ^{\prime }$
. By diagram (4.10) and the inclusions
 $$ \begin{align*} \breve{R}_{\tau,\mathcal{O}_{\mathbb{C}_{p}}}\supseteq \tilde{R}_{\tau,\mathcal{O}_{\mathbb{C}_{p}}}\subseteq\mathcal{O}_{\mathcal{K}_{\tau}}, \end{align*} $$
$$ \begin{align*} \breve{R}_{\tau,\mathcal{O}_{\mathbb{C}_{p}}}\supseteq \tilde{R}_{\tau,\mathcal{O}_{\mathbb{C}_{p}}}\subseteq\mathcal{O}_{\mathcal{K}_{\tau}}, \end{align*} $$
it is enough to show the equality of the lemma after pulling back to
![]() $\mathrm {Spf}\left (\mathcal {O}_{\mathcal {K}_{\tau }}\right )$
.
$\mathrm {Spf}\left (\mathcal {O}_{\mathcal {K}_{\tau }}\right )$
.
Choose an element
![]() $\xi _{\mathfrak {m}}\in (x\mathfrak {m}\mathfrak {c})^{-1}$
such that the map
$\xi _{\mathfrak {m}}\in (x\mathfrak {m}\mathfrak {c})^{-1}$
such that the map
![]() $\rho $
sends the image of
$\rho $
sends the image of
![]() $\xi _{\mathfrak {m}}$
to
$\xi _{\mathfrak {m}}$
to
![]() $1\in \mathfrak {o}/\mathfrak {m}$
. For any
$1\in \mathfrak {o}/\mathfrak {m}$
. For any
 $\zeta \in \mu _{\mathfrak {m}}\left (\bar {\mathbb {Q}}_{p}\right )$
, we define elements Q and
$\zeta \in \mu _{\mathfrak {m}}\left (\bar {\mathbb {Q}}_{p}\right )$
, we define elements Q and
![]() $Q\zeta $
of
$Q\zeta $
of
 $\mathcal {D}_{F}^{-1}\otimes \mathbb {G}_{\mathrm {m}}\left (\hat {R}^{0}_{x^{-1},\tau }\right )$
by
$\mathcal {D}_{F}^{-1}\otimes \mathbb {G}_{\mathrm {m}}\left (\hat {R}^{0}_{x^{-1},\tau }\right )$
by
respectively. Let
![]() $\mathcal {H}_{Q,\zeta }$
be the
$\mathcal {H}_{Q,\zeta }$
be the
![]() $\mathfrak {m}$
-cyclic
$\mathfrak {m}$
-cyclic
![]() $\mathcal {O}_{F}$
-subgroup of the Tate object
$\mathcal {O}_{F}$
-subgroup of the Tate object
![]() $\mathrm {Tate}_{\mathfrak {o},(x\mathfrak {c})^{-1}}(q)\rvert _{\mathcal {O}_{\mathcal {K}_{\tau }}}$
generated by the image of
$\mathrm {Tate}_{\mathfrak {o},(x\mathfrak {c})^{-1}}(q)\rvert _{\mathcal {O}_{\mathcal {K}_{\tau }}}$
generated by the image of
![]() $Q\zeta $
. Then, over
$Q\zeta $
. Then, over
![]() $\mathrm {Spec}\left (\mathcal {O}_{\mathcal {K}_{\tau }}\right )$
, the
$\mathrm {Spec}\left (\mathcal {O}_{\mathcal {K}_{\tau }}\right )$
, the
![]() $\mathfrak {m}$
-cyclic
$\mathfrak {m}$
-cyclic
![]() $\mathcal {O}_{F}$
-subgroup schemes of
$\mathcal {O}_{F}$
-subgroup schemes of
![]() $\mathrm {Tate}_{\mathfrak {o},(x\mathfrak {c})^{-1}}(q)$
are exactly
$\mathrm {Tate}_{\mathfrak {o},(x\mathfrak {c})^{-1}}(q)$
are exactly
 $$ \begin{align*} \mu_{\mathfrak{m}},\qquad \mathcal{H}_{Q,\zeta}\quad \left(\zeta\in \mu_{\mathfrak{m}}\left(\bar{\mathbb{Q}}_{p}\right)\right), \end{align*} $$
$$ \begin{align*} \mu_{\mathfrak{m}},\qquad \mathcal{H}_{Q,\zeta}\quad \left(\zeta\in \mu_{\mathfrak{m}}\left(\bar{\mathbb{Q}}_{p}\right)\right), \end{align*} $$
where the former is the closed subgroup scheme induced by
 $\mu _{\mathfrak {m}}\subseteq \mathcal {D}_{F}^{-1}\otimes \mathbb {G}_{\mathrm {m}}$
. Then the pullback of
$\mu _{\mathfrak {m}}\subseteq \mathcal {D}_{F}^{-1}\otimes \mathbb {G}_{\mathrm {m}}$
. Then the pullback of
![]() $(T_{\mathfrak {m}} f)_{\mathfrak {c}}(q)$
is equal to
$(T_{\mathfrak {m}} f)_{\mathfrak {c}}(q)$
is equal to
 $$ \begin{align*} \left(L_{x} T_{\mathfrak{m}} f_{\mathfrak{c}^{\prime}}\right)\left(\mathrm{Tate}_{\mathfrak{o},\mathfrak{c}^{-1}}(q),\lambda_{\mathfrak{o},\mathfrak{c}^{-1}}\right)&=\nu(x) \left(T_{\mathfrak{m}} f_{\mathfrak{c}^{\prime}}\right)\left(\mathrm{Tate}_{\mathfrak{o},\mathfrak{c}^{-1}}(q),x^{-1}\lambda_{\mathfrak{o},\mathfrak{c}^{-1}}\right)\\ &=\nu(x) \left(T_{\mathfrak{m}} f_{\mathfrak{c}^{\prime}}\right)\left(\mathrm{Tate}_{\mathfrak{o},(x\mathfrak{c})^{-1}}(q^{x}),\lambda_{\mathfrak{o},(x\mathfrak{c})^{-1}}\right), \end{align*} $$
$$ \begin{align*} \left(L_{x} T_{\mathfrak{m}} f_{\mathfrak{c}^{\prime}}\right)\left(\mathrm{Tate}_{\mathfrak{o},\mathfrak{c}^{-1}}(q),\lambda_{\mathfrak{o},\mathfrak{c}^{-1}}\right)&=\nu(x) \left(T_{\mathfrak{m}} f_{\mathfrak{c}^{\prime}}\right)\left(\mathrm{Tate}_{\mathfrak{o},\mathfrak{c}^{-1}}(q),x^{-1}\lambda_{\mathfrak{o},\mathfrak{c}^{-1}}\right)\\ &=\nu(x) \left(T_{\mathfrak{m}} f_{\mathfrak{c}^{\prime}}\right)\left(\mathrm{Tate}_{\mathfrak{o},(x\mathfrak{c})^{-1}}(q^{x}),\lambda_{\mathfrak{o},(x\mathfrak{c})^{-1}}\right), \end{align*} $$
which equals
 $$ \begin{align*} \frac{\nu(x)}{\mathrm{N}_{F/\mathbb{Q}}(\mathfrak{m})}\left( f_{\mathfrak{c}^{\prime}} \left(\mathrm{Tate}_{\mathfrak{o},(x\mathfrak{c})^{-1}}(q^{x})/\mu_{\mathfrak{m}}\right)+\sum_{\zeta\in\mu_{\mathfrak{m}}\left(\bar{\mathbb{Q}}_{p}\right)}f_{\mathfrak{c}^{\prime}}\left(\mathrm{Tate}_{\mathfrak{o},(x\mathfrak{c})^{-1}}(q^{x})/\mathcal{H}_{Q,\zeta}\rvert_{q^{x}}\right) \right). \end{align*} $$
$$ \begin{align*} \frac{\nu(x)}{\mathrm{N}_{F/\mathbb{Q}}(\mathfrak{m})}\left( f_{\mathfrak{c}^{\prime}} \left(\mathrm{Tate}_{\mathfrak{o},(x\mathfrak{c})^{-1}}(q^{x})/\mu_{\mathfrak{m}}\right)+\sum_{\zeta\in\mu_{\mathfrak{m}}\left(\bar{\mathbb{Q}}_{p}\right)}f_{\mathfrak{c}^{\prime}}\left(\mathrm{Tate}_{\mathfrak{o},(x\mathfrak{c})^{-1}}(q^{x})/\mathcal{H}_{Q,\zeta}\rvert_{q^{x}}\right) \right). \end{align*} $$
For the first term, we have the exact sequence

For any
![]() $\xi \in (x\mathfrak {c})^{-1}$
, the natural map
$\xi \in (x\mathfrak {c})^{-1}$
, the natural map
 $\mathcal {D}_{F}^{-1}\otimes \mathbb {G}_{\mathrm {m}}\to \mathfrak {m}^{-1}\mathcal {D}_{F}^{-1}\otimes \mathbb {G}_{\mathrm {m}}$
sends the
$\mathcal {D}_{F}^{-1}\otimes \mathbb {G}_{\mathrm {m}}\to \mathfrak {m}^{-1}\mathcal {D}_{F}^{-1}\otimes \mathbb {G}_{\mathrm {m}}$
sends the
 $\hat {R}_{x^{-1},\tau }^{0}$
-valued point
$\hat {R}_{x^{-1},\tau }^{0}$
-valued point
 $\left (\mathfrak {X}^{\eta }\mapsto q^{\xi \eta }\ (\eta \in \mathfrak {o})\right )$
to
$\left (\mathfrak {X}^{\eta }\mapsto q^{\xi \eta }\ (\eta \in \mathfrak {o})\right )$
to
 $\left (\mathfrak {X}^{\eta }\mapsto q^{\xi \eta }\ (\eta \in \mathfrak {m})\right )$
, and this gives an isomorphism
$\left (\mathfrak {X}^{\eta }\mapsto q^{\xi \eta }\ (\eta \in \mathfrak {m})\right )$
, and this gives an isomorphism
compatible with natural additional structures. This implies that the evaluation
 $f_{\mathfrak {c}^{\prime }} \left (\mathrm {Tate}_{\mathfrak {o},(x\mathfrak {c})^{-1}}(q^{x})/\mu _{\mathfrak {m}}\right )$
equals
$f_{\mathfrak {c}^{\prime }} \left (\mathrm {Tate}_{\mathfrak {o},(x\mathfrak {c})^{-1}}(q^{x})/\mu _{\mathfrak {m}}\right )$
equals
 $$ \begin{align*} f_{\mathfrak{c}^{\prime}} (\mathrm{Tate}_{\mathfrak{m},(x\mathfrak{c})^{-1}}(q^{x}),&\lambda_{\mathfrak{m},(x\mathfrak{c})^{-1}})\\ &=f_{\mathfrak{c}^{\prime}} \left(\mathfrak{m}^{-1}\otimes_{\mathcal{O}_{F}} \mathrm{Tate}_{\mathfrak{o},\mathfrak{m}(x\mathfrak{c})^{-1}}(q^{x}),\mathfrak{m}^{2} \lambda_{\mathfrak{o},\mathfrak{m}(x\mathfrak{c})^{-1}}\right)\\ &=\frac{\mathrm{N}_{F/\mathbb{Q}}(\mathfrak{m})^{2}}{\nu(y)}\left(L_{y} S_{\mathfrak{m}} f_{\mathfrak{c}^{\prime}}\right)\left(\mathrm{Tate}_{\mathfrak{o},(\mathfrak{c}^{\prime\prime})^{-1}}\left(q^{xy^{-1}}\right),\lambda_{\mathfrak{o},(\mathfrak{c}^{\prime\prime})^{-1}}\right)\\ &=\frac{\mathrm{N}_{F/\mathbb{Q}}(\mathfrak{m})^{2}\Phi(\mathfrak{m})}{\nu(y)} f_{\mathfrak{c}^{\prime\prime}}\left(\mathrm{Tate}_{\mathfrak{o},(\mathfrak{c}^{\prime\prime})^{-1}}\left(q^{xy^{-1}}\right)\right). \end{align*} $$
$$ \begin{align*} f_{\mathfrak{c}^{\prime}} (\mathrm{Tate}_{\mathfrak{m},(x\mathfrak{c})^{-1}}(q^{x}),&\lambda_{\mathfrak{m},(x\mathfrak{c})^{-1}})\\ &=f_{\mathfrak{c}^{\prime}} \left(\mathfrak{m}^{-1}\otimes_{\mathcal{O}_{F}} \mathrm{Tate}_{\mathfrak{o},\mathfrak{m}(x\mathfrak{c})^{-1}}(q^{x}),\mathfrak{m}^{2} \lambda_{\mathfrak{o},\mathfrak{m}(x\mathfrak{c})^{-1}}\right)\\ &=\frac{\mathrm{N}_{F/\mathbb{Q}}(\mathfrak{m})^{2}}{\nu(y)}\left(L_{y} S_{\mathfrak{m}} f_{\mathfrak{c}^{\prime}}\right)\left(\mathrm{Tate}_{\mathfrak{o},(\mathfrak{c}^{\prime\prime})^{-1}}\left(q^{xy^{-1}}\right),\lambda_{\mathfrak{o},(\mathfrak{c}^{\prime\prime})^{-1}}\right)\\ &=\frac{\mathrm{N}_{F/\mathbb{Q}}(\mathfrak{m})^{2}\Phi(\mathfrak{m})}{\nu(y)} f_{\mathfrak{c}^{\prime\prime}}\left(\mathrm{Tate}_{\mathfrak{o},(\mathfrak{c}^{\prime\prime})^{-1}}\left(q^{xy^{-1}}\right)\right). \end{align*} $$
For the second term, the subgroup
 $$ \begin{align*} \left\{\left(\mathfrak{X}^{\eta}\mapsto q^{\xi\eta}\zeta^{\rho(\xi\eta)}\ (\eta\in \mathfrak{o})\right)\mid \xi\in (\mathfrak{c}^{\prime})^{-1}\right\}\subseteq \mathcal{D}_{F}^{-1}\otimes\mathbb{G}_{\mathrm{m}}\left(\hat{R}_{x^{-1},\tau}^{0}\right) \end{align*} $$
$$ \begin{align*} \left\{\left(\mathfrak{X}^{\eta}\mapsto q^{\xi\eta}\zeta^{\rho(\xi\eta)}\ (\eta\in \mathfrak{o})\right)\mid \xi\in (\mathfrak{c}^{\prime})^{-1}\right\}\subseteq \mathcal{D}_{F}^{-1}\otimes\mathbb{G}_{\mathrm{m}}\left(\hat{R}_{x^{-1},\tau}^{0}\right) \end{align*} $$
is generated by
![]() $Q\zeta $
and the image of the subgroup
$Q\zeta $
and the image of the subgroup
 $$ \begin{align*} \left\{\left(\mathfrak{X}^{\eta}\mapsto q^{\xi\eta}\ (\eta\in \mathfrak{o})\right)\mid \xi\in (x\mathfrak{c})^{-1}\right\}\subseteq \mathcal{D}_{F}^{-1}\otimes\mathbb{G}_{\mathrm{m}}\left(\hat{R}_{x^{-1},\sigma}^{0}\right) \end{align*} $$
$$ \begin{align*} \left\{\left(\mathfrak{X}^{\eta}\mapsto q^{\xi\eta}\ (\eta\in \mathfrak{o})\right)\mid \xi\in (x\mathfrak{c})^{-1}\right\}\subseteq \mathcal{D}_{F}^{-1}\otimes\mathbb{G}_{\mathrm{m}}\left(\hat{R}_{x^{-1},\sigma}^{0}\right) \end{align*} $$
via the natural map
 $\hat {R}_{x^{-1},\sigma }^{0}\to \hat {R}_{x^{-1},\tau }^{0}$
. This yields an isomorphism
$\hat {R}_{x^{-1},\sigma }^{0}\to \hat {R}_{x^{-1},\tau }^{0}$
. This yields an isomorphism
compatible with natural additional structures. Hence the lemma follows.
A similar proof also gives the following variant for
![]() $\mathfrak {m}\mid Np$
:
$\mathfrak {m}\mid Np$
:
Lemma 4.5.
-
(1) For any maximal ideal
 $\mathfrak {m}\mid N$
, take any element
$\mathfrak {m}\mid N$
, take any element
 $x\in F^{\times ,+,(p)}$
satisfying
$x\in F^{\times ,+,(p)}$
satisfying
 $\mathfrak {c}^{\prime }=x\mathfrak {m} \mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
. Fix an isomorphism of
$\mathfrak {c}^{\prime }=x\mathfrak {m} \mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
. Fix an isomorphism of
 $\mathfrak {o}$
-modules
$\mathfrak {o}$
-modules
 $\rho :(x\mathfrak {m}\mathfrak {c})^{-1}/(x\mathfrak {c})^{-1}\simeq \mathfrak {o}/\mathfrak {m}$
. Then we have
$\rho :(x\mathfrak {m}\mathfrak {c})^{-1}/(x\mathfrak {c})^{-1}\simeq \mathfrak {o}/\mathfrak {m}$
. Then we have  $$ \begin{align*} (T_{\mathfrak{m}} f)_{\mathfrak{c}}(q)=\frac{\nu(x)}{\mathrm{N}_{F/\mathbb{Q}}(\mathfrak{m})}\sum_{\zeta\in \mu_{\mathfrak{m}}\left(\bar{\mathbb{Q}}_{p}\right)}f_{\mathfrak{c}^{\prime}}(q^{x}\zeta^{\rho}). \end{align*} $$
$$ \begin{align*} (T_{\mathfrak{m}} f)_{\mathfrak{c}}(q)=\frac{\nu(x)}{\mathrm{N}_{F/\mathbb{Q}}(\mathfrak{m})}\sum_{\zeta\in \mu_{\mathfrak{m}}\left(\bar{\mathbb{Q}}_{p}\right)}f_{\mathfrak{c}^{\prime}}(q^{x}\zeta^{\rho}). \end{align*} $$
-
(2) For any maximal ideal
 $\mathfrak {p}\mid p$
, take any element
$\mathfrak {p}\mid p$
, take any element
 $x\in F^{\times ,+,(p)}$
satisfying
$x\in F^{\times ,+,(p)}$
satisfying
 $\mathfrak {c}^{\prime }=xx_{\mathfrak {p}}^{-1}\mathfrak {p} \mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
. Fix an isomorphism of
$\mathfrak {c}^{\prime }=xx_{\mathfrak {p}}^{-1}\mathfrak {p} \mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
. Fix an isomorphism of
 $\mathfrak {o}$
-modules
$\mathfrak {o}$
-modules
 $\rho :\left (xx_{\mathfrak {p}}^{-1}\mathfrak {p}\mathfrak {c}\right )^{-1}/\left (xx_{\mathfrak {p}}^{-1}\mathfrak {c}\right )^{-1}\simeq \mathfrak {o}/\mathfrak {p}$
. Then we have
$\rho :\left (xx_{\mathfrak {p}}^{-1}\mathfrak {p}\mathfrak {c}\right )^{-1}/\left (xx_{\mathfrak {p}}^{-1}\mathfrak {c}\right )^{-1}\simeq \mathfrak {o}/\mathfrak {p}$
. Then we have  $$ \begin{align*} (U_{\mathfrak{p}} f)_{\mathfrak{c}}(q)=\frac{\nu(x)}{\mathrm{N}_{F/\mathbb{Q}}(\mathfrak{p})}\sum_{\zeta\in \mu_{\mathfrak{p}}\left(\bar{\mathbb{Q}}_{p}\right)}f_{\mathfrak{c}^{\prime}}\left(q^{xx_{\mathfrak{p}}^{-1}}\zeta^{\rho}\right). \end{align*} $$
$$ \begin{align*} (U_{\mathfrak{p}} f)_{\mathfrak{c}}(q)=\frac{\nu(x)}{\mathrm{N}_{F/\mathbb{Q}}(\mathfrak{p})}\sum_{\zeta\in \mu_{\mathfrak{p}}\left(\bar{\mathbb{Q}}_{p}\right)}f_{\mathfrak{c}^{\prime}}\left(q^{xx_{\mathfrak{p}}^{-1}}\zeta^{\rho}\right). \end{align*} $$
4.2.2 q-Expansion and Hecke eigenvalues
For any
![]() $\xi \in F^{\times }$
, we put
$\xi \in F^{\times }$
, we put
 $\chi _{p}(\xi )=\prod _{\mathfrak {p}\mid p} x_{\mathfrak {p}}^{v_{\mathfrak {p}}(\xi )}$
. For any nonzero ideal
$\chi _{p}(\xi )=\prod _{\mathfrak {p}\mid p} x_{\mathfrak {p}}^{v_{\mathfrak {p}}(\xi )}$
. For any nonzero ideal
![]() $\mathfrak {n}\subseteq \mathfrak {o}$
, take
$\mathfrak {n}\subseteq \mathfrak {o}$
, take
![]() $\eta \in F^{\times ,+}$
satisfying
$\eta \in F^{\times ,+}$
satisfying
 $\mathfrak {c}=\eta ^{-1}\mathfrak {n}\in \left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
and put
$\mathfrak {c}=\eta ^{-1}\mathfrak {n}\in \left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
and put
 $$ \begin{align*} C(\mathfrak{n},f)=\nu\left(\eta^{-1}\chi_{p}(\eta)\right)a_{\mathfrak{o},\mathfrak{c}^{-1}}(f,\eta). \end{align*} $$
$$ \begin{align*} C(\mathfrak{n},f)=\nu\left(\eta^{-1}\chi_{p}(\eta)\right)a_{\mathfrak{o},\mathfrak{c}^{-1}}(f,\eta). \end{align*} $$
By Lemma 4.3, this is independent of the choice of
![]() $\eta $
. Then we have the following variant of [Reference Shimura37, (2.23)] in our setting:
$\eta $
. Then we have the following variant of [Reference Shimura37, (2.23)] in our setting:
Lemma 4.6. For any nonzero ideal
![]() $\mathfrak {l},\mathfrak {n}$
of
$\mathfrak {l},\mathfrak {n}$
of
![]() $\mathfrak {o}$
, we have
$\mathfrak {o}$
, we have
 $$ \begin{align*} C(\mathfrak{n},T_{\mathfrak{l}} f)=\sum_{\mathfrak{l}+\mathfrak{n}\subseteq \mathfrak{a}\subseteq \mathfrak{o}} \mathrm{N}_{F/\mathbb{Q}}(\mathfrak{a})\Phi(\mathfrak{a}) C\left(\mathfrak{a}^{-2}\mathfrak{l}\mathfrak{n},f\right). \end{align*} $$
$$ \begin{align*} C(\mathfrak{n},T_{\mathfrak{l}} f)=\sum_{\mathfrak{l}+\mathfrak{n}\subseteq \mathfrak{a}\subseteq \mathfrak{o}} \mathrm{N}_{F/\mathbb{Q}}(\mathfrak{a})\Phi(\mathfrak{a}) C\left(\mathfrak{a}^{-2}\mathfrak{l}\mathfrak{n},f\right). \end{align*} $$
Proof. We can easily reduce it to the case
![]() $\mathfrak {l}=\mathfrak {m}^{s}$
for some maximal ideal
$\mathfrak {l}=\mathfrak {m}^{s}$
for some maximal ideal
![]() $\mathfrak {m}$
. Consider the case of
$\mathfrak {m}$
. Consider the case of
![]() $\mathfrak {m}\nmid Np$
and
$\mathfrak {m}\nmid Np$
and
![]() $s=1$
. We follow the notation of Lemma 4.4. Since
$s=1$
. We follow the notation of Lemma 4.4. Since
![]() $x^{-1}\eta \in (x\mathfrak {c})^{-1}$
, we have
$x^{-1}\eta \in (x\mathfrak {c})^{-1}$
, we have
 $$ \begin{align*} \sum_{\zeta\in \mu_{\mathfrak{m}}\left(\bar{\mathbb{Q}}_{p}\right)}\zeta^{\rho\left(x^{-1}\eta\right)}= \mathrm{N}_{F/\mathbb{Q}}(\mathfrak{m}). \end{align*} $$
$$ \begin{align*} \sum_{\zeta\in \mu_{\mathfrak{m}}\left(\bar{\mathbb{Q}}_{p}\right)}\zeta^{\rho\left(x^{-1}\eta\right)}= \mathrm{N}_{F/\mathbb{Q}}(\mathfrak{m}). \end{align*} $$
Moreover,
![]() $x^{-1}y\eta \in (\mathfrak {c}^{\prime \prime })^{-1}$
if and only if
$x^{-1}y\eta \in (\mathfrak {c}^{\prime \prime })^{-1}$
if and only if
![]() $\mathfrak {m} \mid \mathfrak {n}$
. Thus Lemma 4.4 implies
$\mathfrak {m} \mid \mathfrak {n}$
. Thus Lemma 4.4 implies
 $$ \begin{align*} C(\mathfrak{n}, T_{\mathfrak{m}} f)= \begin{cases} \mathrm{N}_{F/\mathbb{Q}}(\mathfrak{m})\Phi(\mathfrak{m}) C\left(\mathfrak{m}^{-1}\mathfrak{n},f\right)+C(\mathfrak{m}\mathfrak{n},f)& (\mathfrak{m} \mid \mathfrak{n})\\ C(\mathfrak{m}\mathfrak{n},f) & (\mathfrak{m} \nmid \mathfrak{n}) \end{cases} \end{align*} $$
$$ \begin{align*} C(\mathfrak{n}, T_{\mathfrak{m}} f)= \begin{cases} \mathrm{N}_{F/\mathbb{Q}}(\mathfrak{m})\Phi(\mathfrak{m}) C\left(\mathfrak{m}^{-1}\mathfrak{n},f\right)+C(\mathfrak{m}\mathfrak{n},f)& (\mathfrak{m} \mid \mathfrak{n})\\ C(\mathfrak{m}\mathfrak{n},f) & (\mathfrak{m} \nmid \mathfrak{n}) \end{cases} \end{align*} $$
and the lemma follows for this case. The case of
![]() $\mathfrak {m}\mid Np$
and
$\mathfrak {m}\mid Np$
and
![]() $s=1$
can be shown similarly from Lemma 4.5. For
$s=1$
can be shown similarly from Lemma 4.5. For
![]() $s\geq 2$
, using relation (3.8) we can show the lemma by an induction in the same way as the classical case.
$s\geq 2$
, using relation (3.8) we can show the lemma by an induction in the same way as the classical case.
Proposition 4.7. For any
 $\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
and any
$\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
and any
 $\eta \in \left (\mathfrak {c}^{-1}\right )^{+}$
, put
$\eta \in \left (\mathfrak {c}^{-1}\right )^{+}$
, put
![]() $\mathfrak {n}=\eta \mathfrak {c}\subseteq \mathfrak {o}$
. Then we have
$\mathfrak {n}=\eta \mathfrak {c}\subseteq \mathfrak {o}$
. Then we have
 $$ \begin{align*} a_{\mathfrak{o},\mathfrak{c}^{-1}}(f,\eta)=\nu\left(\eta \chi_{p}(\eta)^{-1}\right) \Lambda(\mathfrak{n}) a_{\mathfrak{o},\mathfrak{o}}(f,1). \end{align*} $$
$$ \begin{align*} a_{\mathfrak{o},\mathfrak{c}^{-1}}(f,\eta)=\nu\left(\eta \chi_{p}(\eta)^{-1}\right) \Lambda(\mathfrak{n}) a_{\mathfrak{o},\mathfrak{o}}(f,1). \end{align*} $$
Proof. We have
 $a_{\mathfrak {o},\mathfrak {c}^{-1}}(f,\eta )=\nu \left (\eta \chi _{p}(\eta )^{-1}\right ) C(\mathfrak {n},f)$
and
$a_{\mathfrak {o},\mathfrak {c}^{-1}}(f,\eta )=\nu \left (\eta \chi _{p}(\eta )^{-1}\right ) C(\mathfrak {n},f)$
and
![]() $C(\mathfrak {o}, f)=a_{\mathfrak {o},\mathfrak {o}}(f,1)$
. By Lemma 4.6, we obtain
$C(\mathfrak {o}, f)=a_{\mathfrak {o},\mathfrak {o}}(f,1)$
. By Lemma 4.6, we obtain
 $$ \begin{align*} \Lambda(\mathfrak{n})a_{\mathfrak{o},\mathfrak{o}}(f,1)&=\Lambda(\mathfrak{n})C(\mathfrak{o},f)=C(\mathfrak{o}, T_{\mathfrak{n}} f)\\ &=C(\mathfrak{n},f)=\nu\left(\eta^{-1}\chi_{p}(\eta)\right) a_{\mathfrak{o},\mathfrak{c}^{-1}}(f,\eta), \end{align*} $$
$$ \begin{align*} \Lambda(\mathfrak{n})a_{\mathfrak{o},\mathfrak{o}}(f,1)&=\Lambda(\mathfrak{n})C(\mathfrak{o},f)=C(\mathfrak{o}, T_{\mathfrak{n}} f)\\ &=C(\mathfrak{n},f)=\nu\left(\eta^{-1}\chi_{p}(\eta)\right) a_{\mathfrak{o},\mathfrak{c}^{-1}}(f,\eta), \end{align*} $$
from which the proposition follows.
4.3 q-Expansion and integrality
First we show the following lemma:
Lemma 4.8. Let
![]() $\mathfrak {X}$
be a quasi-compact separated admissible formal scheme over
$\mathfrak {X}$
be a quasi-compact separated admissible formal scheme over
![]() $\mathcal {O}_{\mathbb {C}_{p}}$
. Let
$\mathcal {O}_{\mathbb {C}_{p}}$
. Let
![]() $\mathfrak {F}$
be an invertible sheaf on
$\mathfrak {F}$
be an invertible sheaf on
![]() $\mathfrak {X}$
. We denote by
$\mathfrak {X}$
. We denote by
![]() $\mathfrak {X}_{\bar {\mathbb {F}}_{p}}$
the special fiber of
$\mathfrak {X}_{\bar {\mathbb {F}}_{p}}$
the special fiber of
![]() $\mathfrak {X}$
and by
$\mathfrak {X}$
and by
![]() $\mathfrak {F}_{\bar {\mathbb {F}}_{p}}$
the pullback of
$\mathfrak {F}_{\bar {\mathbb {F}}_{p}}$
the pullback of
![]() $\mathfrak {F}$
to
$\mathfrak {F}$
to
![]() $\mathfrak {X}_{\bar {\mathbb {F}}_{p}}$
.
$\mathfrak {X}_{\bar {\mathbb {F}}_{p}}$
.
-
(1) Suppose that
 $\mathfrak {X}^{\mathrm {rig}}$
is reduced and
$\mathfrak {X}^{\mathrm {rig}}$
is reduced and
 $\mathfrak {X}$
is integrally closed in
$\mathfrak {X}$
is integrally closed in
 $\mathfrak {X}^{\mathrm {rig}}$
. Then for any nonzero element
$\mathfrak {X}^{\mathrm {rig}}$
. Then for any nonzero element
 $f\in H^{0}(\mathfrak {X},\mathfrak {F})[1/p]$
, the
$f\in H^{0}(\mathfrak {X},\mathfrak {F})[1/p]$
, the
 $\mathcal {O}_{\mathbb {C}_{p}}$
-submodule of
$\mathcal {O}_{\mathbb {C}_{p}}$
-submodule of
 $\mathbb {C}_{p}$
is principal.
$\mathbb {C}_{p}$
is principal. $$ \begin{align*} I=\left\{x\in\mathbb{C}_{p}\mid x f\in H^{0}(\mathfrak{X},\mathfrak{F})\right\} \end{align*} $$
$$ \begin{align*} I=\left\{x\in\mathbb{C}_{p}\mid x f\in H^{0}(\mathfrak{X},\mathfrak{F})\right\} \end{align*} $$
-
(2) Let g be an element of
 $H^{0}(\mathfrak {X},\mathfrak {F})$
. Suppose that the image of g by the map is zero. Then there exists
$H^{0}(\mathfrak {X},\mathfrak {F})$
. Suppose that the image of g by the map is zero. Then there exists $$ \begin{align*} H^{0}(\mathfrak{X},\mathfrak{F})\to H^{0}\left(\mathfrak{X}_{\bar{\mathbb{F}}_{p}},\mathfrak{F}_{\bar{\mathbb{F}}_{p}}\right) \end{align*} $$
$$ \begin{align*} H^{0}(\mathfrak{X},\mathfrak{F})\to H^{0}\left(\mathfrak{X}_{\bar{\mathbb{F}}_{p}},\mathfrak{F}_{\bar{\mathbb{F}}_{p}}\right) \end{align*} $$
 $x\in m_{\mathbb {C}_{p}}$
satisfying
$x\in m_{\mathbb {C}_{p}}$
satisfying
 $g\in xH^{0}(\mathfrak {X},\mathfrak {F})$
.
$g\in xH^{0}(\mathfrak {X},\mathfrak {F})$
.
Proof. For the first assertion, take a finite covering
![]() $\mathfrak {X}=\bigcup _{i=1}^{r} \mathfrak {U}_{i}$
by formal affine open subschemes
$\mathfrak {X}=\bigcup _{i=1}^{r} \mathfrak {U}_{i}$
by formal affine open subschemes
![]() $\mathfrak {U}_{i}=\mathrm {Spf}(\mathfrak {A}_{i})$
such that
$\mathfrak {U}_{i}=\mathrm {Spf}(\mathfrak {A}_{i})$
such that
![]() $\mathfrak {F}\rvert _{\mathfrak {U}_{i}}$
is trivial. Since
$\mathfrak {F}\rvert _{\mathfrak {U}_{i}}$
is trivial. Since
![]() $\mathfrak {X}$
is separated, the intersection
$\mathfrak {X}$
is separated, the intersection
![]() $\mathfrak {U}_{i,j}=\mathfrak {U}_{i}\cap \mathfrak {U}_{j}$
is also affine. Put
$\mathfrak {U}_{i,j}=\mathfrak {U}_{i}\cap \mathfrak {U}_{j}$
is also affine. Put
![]() $A_{i}=\mathfrak {A}_{i}[1/p]$
,
$A_{i}=\mathfrak {A}_{i}[1/p]$
,
![]() $\mathfrak {M}_{i}=\Gamma (\mathfrak {U}_{i},\mathfrak {F})$
, and
$\mathfrak {M}_{i}=\Gamma (\mathfrak {U}_{i},\mathfrak {F})$
, and
![]() $\mathfrak {M}_{i,j}=\Gamma \left (\mathfrak {U}_{i,j},\mathfrak {F}\right )$
. Then we have a commutative diagram
$\mathfrak {M}_{i,j}=\Gamma \left (\mathfrak {U}_{i,j},\mathfrak {F}\right )$
. Then we have a commutative diagram

where the rows are exact and the vertical arrows are injective. Put
![]() $I_{i}=\left \{x\in \mathbb {C}_{p}\mid x f\rvert _{\mathfrak {U}_{i}} \in \mathfrak {M}_{i}\right \}$
. Note that
$I_{i}=\left \{x\in \mathbb {C}_{p}\mid x f\rvert _{\mathfrak {U}_{i}} \in \mathfrak {M}_{i}\right \}$
. Note that
![]() $I_{i}=\mathbb {C}_{p}$
if
$I_{i}=\mathbb {C}_{p}$
if
![]() $f\rvert _{\mathfrak {U}_{i}}=0$
. Since the diagram implies
$f\rvert _{\mathfrak {U}_{i}}=0$
. Since the diagram implies
![]() $I=\bigcap _{i=1}^{r} I_{i}$
, it is enough to show that
$I=\bigcap _{i=1}^{r} I_{i}$
, it is enough to show that
![]() $I_{i}$
is principal if
$I_{i}$
is principal if
![]() $f\rvert _{\mathfrak {U}_{i}}\neq 0$
.
$f\rvert _{\mathfrak {U}_{i}}\neq 0$
.
By choosing a trivialization, we identify
![]() $\mathfrak {M}_{i}$
with
$\mathfrak {M}_{i}$
with
![]() $\mathfrak {A}_{i}$
and
$\mathfrak {A}_{i}$
and
![]() $f\rvert _{\mathfrak {U}_{i}}\in \mathfrak {M}_{i}[1/p]$
with a nonzero element
$f\rvert _{\mathfrak {U}_{i}}\in \mathfrak {M}_{i}[1/p]$
with a nonzero element
![]() $g_{i}\in A_{i}$
. Note that
$g_{i}\in A_{i}$
. Note that
![]() $A_{i}$
is a reduced
$A_{i}$
is a reduced
![]() $\mathbb {C}_{p}$
-affinoid algebra. Since
$\mathbb {C}_{p}$
-affinoid algebra. Since
![]() $\mathfrak {A}_{i}$
is an admissible formal
$\mathfrak {A}_{i}$
is an admissible formal
![]() $\mathcal {O}_{\mathbb {C}_{p}}$
-algebra which is integrally closed in
$\mathcal {O}_{\mathbb {C}_{p}}$
-algebra which is integrally closed in
![]() $A_{i}$
, [Reference Bosch, Güntzer and Remmert10, remark after Proposition 6.3.4/1] implies
$A_{i}$
, [Reference Bosch, Güntzer and Remmert10, remark after Proposition 6.3.4/1] implies
![]() $A_{i}^{\circ }=\mathfrak {A}_{i}$
. Thus for any
$A_{i}^{\circ }=\mathfrak {A}_{i}$
. Thus for any
![]() $x \in \mathbb {C}_{p}$
, we have
$x \in \mathbb {C}_{p}$
, we have
where
![]() $\lvert g_{i}\rvert _{\sup }$
is the supremum norm of
$\lvert g_{i}\rvert _{\sup }$
is the supremum norm of
![]() $g_{i}$
on
$g_{i}$
on
![]() $\mathrm {Sp}(A_{i})$
. By the maximum modulus principle, there exists a nonzero element
$\mathrm {Sp}(A_{i})$
. By the maximum modulus principle, there exists a nonzero element
![]() $\delta \in \mathbb {C}_{p}$
satisfying
$\delta \in \mathbb {C}_{p}$
satisfying
![]() $\lvert \delta \rvert =\lvert g_{i}\rvert _{\sup }$
. Hence we obtain
$\lvert \delta \rvert =\lvert g_{i}\rvert _{\sup }$
. Hence we obtain
 $$ \begin{align*} I_{i}=\left\{x\in \mathbb{C}_{p}\mid \lvert x\rvert\leq \lvert\delta\rvert^{-1}\right\}=\delta^{-1}\mathcal{O}_{\mathbb{C}_{p}}, \end{align*} $$
$$ \begin{align*} I_{i}=\left\{x\in \mathbb{C}_{p}\mid \lvert x\rvert\leq \lvert\delta\rvert^{-1}\right\}=\delta^{-1}\mathcal{O}_{\mathbb{C}_{p}}, \end{align*} $$
and the first assertion follows.
For the second assertion, consider the covering
![]() $\mathfrak {X}=\bigcup _{i=1}^{r} \mathfrak {U}_{i}$
as before. Since the reduction of
$\mathfrak {X}=\bigcup _{i=1}^{r} \mathfrak {U}_{i}$
as before. Since the reduction of
![]() $g\rvert _{\mathfrak {U}_{i}}$
is also zero, we can write
$g\rvert _{\mathfrak {U}_{i}}$
is also zero, we can write
![]() $g\rvert _{\mathfrak {U}_{i}}=x_{i} h_{i}$
with some
$g\rvert _{\mathfrak {U}_{i}}=x_{i} h_{i}$
with some
![]() $x_{i}\in m_{\mathbb {C}_{p}}$
and
$x_{i}\in m_{\mathbb {C}_{p}}$
and
![]() $h_{i}\in \mathfrak {M}_{i}$
. Replacing
$h_{i}\in \mathfrak {M}_{i}$
. Replacing
![]() $x_{i}$
by a generator x of the ideal
$x_{i}$
by a generator x of the ideal
![]() $(x_{1},\dotsc ,x_{r})$
, we may assume
$(x_{1},\dotsc ,x_{r})$
, we may assume
![]() $g\rvert _{\mathfrak {U}_{i}}=x h_{i}$
for any i. Since
$g\rvert _{\mathfrak {U}_{i}}=x h_{i}$
for any i. Since
![]() $\mathfrak {M}_{i}$
and
$\mathfrak {M}_{i}$
and
![]() $\mathfrak {M}_{i,j}$
are torsion-free
$\mathfrak {M}_{i,j}$
are torsion-free
![]() $\mathcal {O}_{\mathbb {C}_{p}}$
-modules, the elements
$\mathcal {O}_{\mathbb {C}_{p}}$
-modules, the elements
![]() $h_{i}$
can be glued to define
$h_{i}$
can be glued to define
![]() $h\in H^{0}(\mathfrak {X},\mathfrak {F})$
. Then we obtain
$h\in H^{0}(\mathfrak {X},\mathfrak {F})$
. Then we obtain
![]() $g=xh$
and the second assertion follows.
$g=xh$
and the second assertion follows.
Let
![]() $\kappa \in \mathcal {W}\left (\mathbb {C}_{p}\right )$
be any n-analytic weight. Put
$\kappa \in \mathcal {W}\left (\mathbb {C}_{p}\right )$
be any n-analytic weight. Put
 $$ \begin{align*} \mathbf{M}(\mu_{N},\mathfrak{c},\kappa)(0):=H^{0}\left(\bar{\mathfrak{M}}(\mu_{N},\mathfrak{c})(0)_{\mathcal{O}_{\mathbb{C}_{p}}},\mathbf{\Omega}^{\kappa}\right)\subseteq M(\mu_{N},\mathfrak{c},\kappa)(0). \end{align*} $$
$$ \begin{align*} \mathbf{M}(\mu_{N},\mathfrak{c},\kappa)(0):=H^{0}\left(\bar{\mathfrak{M}}(\mu_{N},\mathfrak{c})(0)_{\mathcal{O}_{\mathbb{C}_{p}}},\mathbf{\Omega}^{\kappa}\right)\subseteq M(\mu_{N},\mathfrak{c},\kappa)(0). \end{align*} $$
This is an
![]() $\mathcal {O}_{\mathbb {C}_{p}}$
-lattice of the Banach
$\mathcal {O}_{\mathbb {C}_{p}}$
-lattice of the Banach
![]() $\mathbb {C}_{p}$
-module
$\mathbb {C}_{p}$
-module
![]() $M(\mu _{N},\mathfrak {c},\kappa )(0)$
. Consider the cusp
$M(\mu _{N},\mathfrak {c},\kappa )(0)$
. Consider the cusp
 $\left (\mathfrak {o},\mathfrak {c}^{-1},\mathrm {id}\right )$
, the fixed cone decomposition
$\left (\mathfrak {o},\mathfrak {c}^{-1},\mathrm {id}\right )$
, the fixed cone decomposition
 $\mathscr {C}=\mathscr {C}\left (\mathfrak {o},\mathfrak {c}^{-1}\right )\in \mathrm {Dec}\left (\mathfrak {o},\mathfrak {c}^{-1}\right )$
, and
$\mathscr {C}=\mathscr {C}\left (\mathfrak {o},\mathfrak {c}^{-1}\right )\in \mathrm {Dec}\left (\mathfrak {o},\mathfrak {c}^{-1}\right )$
, and
![]() $\sigma \in \mathscr {C}$
. By the definition of the q-expansion, every coefficient of the q-expansion of
$\sigma \in \mathscr {C}$
. By the definition of the q-expansion, every coefficient of the q-expansion of
![]() $f\in \mathbf {M}(\mu _{N},\mathfrak {c},\kappa )(0)$
is an element of
$f\in \mathbf {M}(\mu _{N},\mathfrak {c},\kappa )(0)$
is an element of
![]() $\mathcal {O}_{\mathbb {C}_{p}}$
. We also have the following converse, which can be considered as a q-expansion principle for our setting:
$\mathcal {O}_{\mathbb {C}_{p}}$
. We also have the following converse, which can be considered as a q-expansion principle for our setting:
Proposition 4.9. Let
![]() $f_{\mathfrak {c}}$
be any element of
$f_{\mathfrak {c}}$
be any element of
![]() $M(\mu _{N},\mathfrak {c},\kappa )(0)$
. If every coefficient of the q-expansion
$M(\mu _{N},\mathfrak {c},\kappa )(0)$
. If every coefficient of the q-expansion
![]() $f_{\mathfrak {c}}(q)$
is in
$f_{\mathfrak {c}}(q)$
is in
![]() $\mathcal {O}_{\mathbb {C}_{p}}$
, then we have
$\mathcal {O}_{\mathbb {C}_{p}}$
, then we have
![]() $f\in \mathbf {M}(\mu _{N},\mathfrak {c},\kappa )(0)$
.
$f\in \mathbf {M}(\mu _{N},\mathfrak {c},\kappa )(0)$
.
Proof. Put
![]() $\bar {\mathfrak {M}}^{\mathrm {ord}}=\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)$
,
$\bar {\mathfrak {M}}^{\mathrm {ord}}=\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(0)$
,
![]() $\bar {\mathfrak {M}}(\Gamma _{1}(p^{n}))^{\mathrm {ord}}=\bar {\mathfrak {M}}(\Gamma _{1}(p^{n}),\mu _{N},\mathfrak {c})(0)$
, and
$\bar {\mathfrak {M}}(\Gamma _{1}(p^{n}))^{\mathrm {ord}}=\bar {\mathfrak {M}}(\Gamma _{1}(p^{n}),\mu _{N},\mathfrak {c})(0)$
, and
 $\mathfrak {IW}^{\mathrm {ord}}=\mathfrak {IW}_{w,\mathfrak {c}}^{+}(0)$
. Recall that
$\mathfrak {IW}^{\mathrm {ord}}=\mathfrak {IW}_{w,\mathfrak {c}}^{+}(0)$
. Recall that
![]() $\mathbf {\Omega }^{\kappa }$
is invertible on
$\mathbf {\Omega }^{\kappa }$
is invertible on
![]() $\bar {\mathfrak {M}}^{\mathrm {ord}}$
. We denote the reduction of
$\bar {\mathfrak {M}}^{\mathrm {ord}}$
. We denote the reduction of
 $\bar {\mathfrak {M}}^{\mathrm {ord}}_{\mathcal {O}_{\mathbb {C}_{p}}}$
by
$\bar {\mathfrak {M}}^{\mathrm {ord}}_{\mathcal {O}_{\mathbb {C}_{p}}}$
by
 $\bar {\mathfrak {M}}^{\mathrm {ord}}_{\bar {\mathbb {F}}_{p}}$
. Consider the commutative diagram
$\bar {\mathfrak {M}}^{\mathrm {ord}}_{\bar {\mathbb {F}}_{p}}$
. Consider the commutative diagram

Recall that
 $f_{\mathfrak {c}}\in \mathcal {O}\left (\mathfrak {IW}^{\mathrm {ord}}_{\mathcal {O}_{\mathbb {C}_{p}}}\right )[1/p]$
. The assumption on
$f_{\mathfrak {c}}\in \mathcal {O}\left (\mathfrak {IW}^{\mathrm {ord}}_{\mathcal {O}_{\mathbb {C}_{p}}}\right )[1/p]$
. The assumption on
![]() $f_{\mathfrak {c}}(q)$
implies
$f_{\mathfrak {c}}(q)$
implies
 $\tau ^{*}_{\mathfrak {o},\mathfrak {c}^{-1}}(f_{\mathfrak {c}}) \in \mathcal {O}\left (\breve {S}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}\right )$
.
$\tau ^{*}_{\mathfrak {o},\mathfrak {c}^{-1}}(f_{\mathfrak {c}}) \in \mathcal {O}\left (\breve {S}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}\right )$
.
Consider the special fiber
 $$ \begin{align*} \bar{\pi}_{w}: \mathfrak{IW}^{\mathrm{ord}}_{\bar{\mathbb{F}}_{p}}\overset{\bar{\gamma}_{n}}{\to} \bar{\mathfrak{M}}(\Gamma_{1}(p^{n}))^{\mathrm{ord}}_{\bar{\mathbb{F}}_{p}} \overset{\bar{h}_{n}}{\to} \bar{\mathfrak{M}}^{\mathrm{ord}}_{\bar{\mathbb{F}}_{p}} \end{align*} $$
$$ \begin{align*} \bar{\pi}_{w}: \mathfrak{IW}^{\mathrm{ord}}_{\bar{\mathbb{F}}_{p}}\overset{\bar{\gamma}_{n}}{\to} \bar{\mathfrak{M}}(\Gamma_{1}(p^{n}))^{\mathrm{ord}}_{\bar{\mathbb{F}}_{p}} \overset{\bar{h}_{n}}{\to} \bar{\mathfrak{M}}^{\mathrm{ord}}_{\bar{\mathbb{F}}_{p}} \end{align*} $$
of the map
![]() $\pi _{w}$
and the closed immersion
$\pi _{w}$
and the closed immersion
 $i:\bar {\mathfrak {M}}^{\mathrm {ord}}_{\bar {\mathbb {F}}_{p}}\to \bar {\mathfrak {M}}^{\mathrm {ord}}_{\mathcal {O}_{\mathbb {C}_{p}}}$
. From the construction of the sheaf
$i:\bar {\mathfrak {M}}^{\mathrm {ord}}_{\bar {\mathbb {F}}_{p}}\to \bar {\mathfrak {M}}^{\mathrm {ord}}_{\mathcal {O}_{\mathbb {C}_{p}}}$
. From the construction of the sheaf
 $\mathbf {\Omega }^{\kappa }\rvert _{\bar {\mathfrak {M}}^{\mathrm {ord}}_{\mathcal {O}_{\mathbb {C}_{p}}}}$
as the fixed part of a
$\mathbf {\Omega }^{\kappa }\rvert _{\bar {\mathfrak {M}}^{\mathrm {ord}}_{\mathcal {O}_{\mathbb {C}_{p}}}}$
as the fixed part of a
![]() $\mathbb {T}(\mathbb {Z}/p^{n}\mathbb {Z})$
-equivariant
$\mathbb {T}(\mathbb {Z}/p^{n}\mathbb {Z})$
-equivariant
![]() $\mathcal {O}_{\mathbb {C}_{p}}$
-flat sheaf on a
$\mathcal {O}_{\mathbb {C}_{p}}$
-flat sheaf on a
![]() $\mathbb {T}(\mathbb {Z}/p^{n}\mathbb {Z})$
-torsor, we see that the subsheaf
$\mathbb {T}(\mathbb {Z}/p^{n}\mathbb {Z})$
-torsor, we see that the subsheaf
 $\mathbf {\Omega }^{\kappa }\rvert _{\bar {\mathfrak {M}}^{\mathrm {ord}}_{\mathcal {O}_{\mathbb {C}_{p}}}}\subseteq (\pi _{w})_{*}\mathcal {O}_{\mathfrak {IW}_{w,\mathfrak {c}}^{+}(0)_{\mathcal {O}_{\mathbb {C}_{p}}}}$
is formal locally a direct summand. Since
$\mathbf {\Omega }^{\kappa }\rvert _{\bar {\mathfrak {M}}^{\mathrm {ord}}_{\mathcal {O}_{\mathbb {C}_{p}}}}\subseteq (\pi _{w})_{*}\mathcal {O}_{\mathfrak {IW}_{w,\mathfrak {c}}^{+}(0)_{\mathcal {O}_{\mathbb {C}_{p}}}}$
is formal locally a direct summand. Since
![]() $\pi _{w}$
is affine, for any morphism of formal schemes
$\pi _{w}$
is affine, for any morphism of formal schemes
 $f:S\to \bar {\mathfrak {M}}^{\mathrm {ord}}_{\mathcal {O}_{\mathbb {C}_{p}}}$
the composite of natural maps
$f:S\to \bar {\mathfrak {M}}^{\mathrm {ord}}_{\mathcal {O}_{\mathbb {C}_{p}}}$
the composite of natural maps
 $$ \begin{align*} f^{*}\left(\mathbf{\Omega}^{\kappa}\rvert_{\bar{\mathfrak{M}}^{\mathrm{ord}}_{\mathcal{O}_{\mathbb{C}_{p}}}}\right)\to f^{*}(\pi_{w})_{*}\mathcal{O}_{\mathfrak{IW}^{\mathrm{ord}}_{\mathcal{O}_{\mathbb{C}_{p}}}}\to \left(\pi_{w}\rvert_{\pi_{w}^{-1}(S)}\right)_{*}\mathcal{O}_{\pi_{w}^{-1}(S)} \end{align*} $$
$$ \begin{align*} f^{*}\left(\mathbf{\Omega}^{\kappa}\rvert_{\bar{\mathfrak{M}}^{\mathrm{ord}}_{\mathcal{O}_{\mathbb{C}_{p}}}}\right)\to f^{*}(\pi_{w})_{*}\mathcal{O}_{\mathfrak{IW}^{\mathrm{ord}}_{\mathcal{O}_{\mathbb{C}_{p}}}}\to \left(\pi_{w}\rvert_{\pi_{w}^{-1}(S)}\right)_{*}\mathcal{O}_{\pi_{w}^{-1}(S)} \end{align*} $$
is injective. This yields a commutative diagram

with injective horizontal arrows, where the base extension
 $\hat {S}_{\mathscr {C},\bar {\mathbb {F}}_{p}}=\hat {S}_{\mathscr {C}}\hat {\otimes }_{k}\bar {\mathbb {F}}_{p}$
is equal to the special fiber of
$\hat {S}_{\mathscr {C},\bar {\mathbb {F}}_{p}}=\hat {S}_{\mathscr {C}}\hat {\otimes }_{k}\bar {\mathbb {F}}_{p}$
is equal to the special fiber of
 $\breve {S}_{\mathscr {C},\mathcal {O}_{\mathbb {C}_{p}}}$
.
$\breve {S}_{\mathscr {C},\mathcal {O}_{\mathbb {C}_{p}}}$
.
On the Tate object
![]() $\mathrm {Tate}_{\mathfrak {o},\mathfrak {c}^{-1}}(q)$
over
$\mathrm {Tate}_{\mathfrak {o},\mathfrak {c}^{-1}}(q)$
over
 $\mathrm {Spec}\left (\breve {R}_{\sigma }\right )$
, we defined the canonical trivialization of the canonical subgroup and that of the
$\mathrm {Spec}\left (\breve {R}_{\sigma }\right )$
, we defined the canonical trivialization of the canonical subgroup and that of the
 $\mathbb {T}_{w}^{0}\left (\breve {S}_{\sigma }\right )$
-set
$\mathbb {T}_{w}^{0}\left (\breve {S}_{\sigma }\right )$
-set
 $\mathfrak {IW}^{\mathrm {ord}}\left (\breve {S}_{\sigma }\right )$
, which are denoted by
$\mathfrak {IW}^{\mathrm {ord}}\left (\breve {S}_{\sigma }\right )$
, which are denoted by
![]() $u_{\mathfrak {o},\mathfrak {c}^{-1}}$
and
$u_{\mathfrak {o},\mathfrak {c}^{-1}}$
and
![]() $\alpha _{\mathfrak {o},\mathfrak {c}^{-1}}$
. For any
$\alpha _{\mathfrak {o},\mathfrak {c}^{-1}}$
. For any
![]() $a\in \mathbb {T}(\mathbb {Z}/p^{n}\mathbb {Z})$
, we fix its lift
$a\in \mathbb {T}(\mathbb {Z}/p^{n}\mathbb {Z})$
, we fix its lift
![]() $\hat {a}\in \mathbb {T}_{w}\left (\mathbb {Z}_{p}\right )$
satisfying
$\hat {a}\in \mathbb {T}_{w}\left (\mathbb {Z}_{p}\right )$
satisfying
![]() $\hat {1}=1$
. Since
$\hat {1}=1$
. Since
![]() $\breve {R}_{\sigma }$
is Noetherian, the moduli interpretation of
$\breve {R}_{\sigma }$
is Noetherian, the moduli interpretation of
![]() $\mathfrak {IW}^{\mathrm {ord}}$
is available over
$\mathfrak {IW}^{\mathrm {ord}}$
is available over
![]() $\breve {R}_{\sigma }$
, and these trivializations give isomorphisms
$\breve {R}_{\sigma }$
, and these trivializations give isomorphisms
 $$ \begin{align*} \breve{S}_{\sigma}\times_{\bar{\mathfrak{M}}^{\mathrm{ord}}} \bar{\mathfrak{M}}(\Gamma_{1}(p^{n}))^{\mathrm{ord}}\simeq \coprod_{a\in \mathbb{T}\left(\mathbb{Z}/p^{n}\mathbb{Z}\right)} \breve{S}_{\sigma},\qquad \pi_{w}^{-1}\left(\breve{S} {}_{\sigma}\right)\simeq \coprod_{a\in \mathbb{T}\left(\mathbb{Z}/p^{n}\mathbb{Z}\right)} \breve{S}_{\sigma}\times\mathbb{T}_{w}^{0}. \end{align*} $$
$$ \begin{align*} \breve{S}_{\sigma}\times_{\bar{\mathfrak{M}}^{\mathrm{ord}}} \bar{\mathfrak{M}}(\Gamma_{1}(p^{n}))^{\mathrm{ord}}\simeq \coprod_{a\in \mathbb{T}\left(\mathbb{Z}/p^{n}\mathbb{Z}\right)} \breve{S}_{\sigma},\qquad \pi_{w}^{-1}\left(\breve{S} {}_{\sigma}\right)\simeq \coprod_{a\in \mathbb{T}\left(\mathbb{Z}/p^{n}\mathbb{Z}\right)} \breve{S}_{\sigma}\times\mathbb{T}_{w}^{0}. \end{align*} $$
The latter is an isomorphism of formal
![]() $\mathbb {T}_{w}^{0}$
-torsors given by
$\mathbb {T}_{w}^{0}$
-torsors given by
 $\left (au_{\mathfrak {o},\mathfrak {c}^{-1}},\hat {a}\alpha _{\mathfrak {o},\mathfrak {c}^{-1}}\right )$
at the a-component. By the base extension, we also have similar isomorphisms over
$\left (au_{\mathfrak {o},\mathfrak {c}^{-1}},\hat {a}\alpha _{\mathfrak {o},\mathfrak {c}^{-1}}\right )$
at the a-component. By the base extension, we also have similar isomorphisms over
![]() $\mathcal {O}_{\mathbb {C}_{p}}$
. Since the latter isomorphism is defined by
$\mathcal {O}_{\mathbb {C}_{p}}$
. Since the latter isomorphism is defined by
 $\left (u_{\mathfrak {o},\mathfrak {c}^{-1}},\alpha _{\mathfrak {o},\mathfrak {c}^{-1}}\right )$
at the component
$\left (u_{\mathfrak {o},\mathfrak {c}^{-1}},\alpha _{\mathfrak {o},\mathfrak {c}^{-1}}\right )$
at the component
![]() $a=1$
, the unit section on this component coincides with the foregoing map
$a=1$
, the unit section on this component coincides with the foregoing map
 $\breve {S}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}} \to \pi _{w}^{-1} \left (\breve {S}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}\right )$
.
$\breve {S}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}} \to \pi _{w}^{-1} \left (\breve {S}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}\right )$
.
For any formal character
![]() $\chi $
of
$\chi $
of
![]() $\mathbb {T}_{w}^{0}$
, the
$\mathbb {T}_{w}^{0}$
, the
![]() $\chi $
-part of the
$\chi $
-part of the
![]() $\mathbb {T}_{w}^{0}$
-representation
$\mathbb {T}_{w}^{0}$
-representation
 $\mathcal {O}\left (\breve {S}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}\times \mathbb {T}_{w}^{0}\right )$
is a free
$\mathcal {O}\left (\breve {S}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}\times \mathbb {T}_{w}^{0}\right )$
is a free
 $\breve {R} {}_{\sigma , \mathcal {O}_{\mathbb {C}_{p}}}$
-module of rank
$\breve {R} {}_{\sigma , \mathcal {O}_{\mathbb {C}_{p}}}$
-module of rank
![]() $1$
with a generator
$1$
with a generator
![]() $s_{\chi }$
. Then we have
$s_{\chi }$
. Then we have
 $$ \begin{align*} f_{\mathfrak{c}}\rvert_{\pi^{-1}_{w}\left(\breve{S}_{\sigma,\mathcal{O}_{\mathbb{C}_{p}}}\right)}\in \prod_{a\in \mathbb{T}\left(\mathbb{Z}/p^{n}\mathbb{Z}\right)} \left(\breve{R}_{\sigma,\mathcal{O}_{\mathbb{C}_{p}}}[1/p]s_{\kappa^{-1}}\right). \end{align*} $$
$$ \begin{align*} f_{\mathfrak{c}}\rvert_{\pi^{-1}_{w}\left(\breve{S}_{\sigma,\mathcal{O}_{\mathbb{C}_{p}}}\right)}\in \prod_{a\in \mathbb{T}\left(\mathbb{Z}/p^{n}\mathbb{Z}\right)} \left(\breve{R}_{\sigma,\mathcal{O}_{\mathbb{C}_{p}}}[1/p]s_{\kappa^{-1}}\right). \end{align*} $$
Write this element as
 $\left (F_{a} s_{\kappa ^{-1}}\right )_{a\in \mathbb {T}\left (\mathbb {Z}/p^{n}\mathbb {Z}\right )}$
with
$\left (F_{a} s_{\kappa ^{-1}}\right )_{a\in \mathbb {T}\left (\mathbb {Z}/p^{n}\mathbb {Z}\right )}$
with
 $F_{a}\in \breve {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}[1/p]$
. Since
$F_{a}\in \breve {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}[1/p]$
. Since
![]() $\kappa (1)=1$
and
$\kappa (1)=1$
and
 $\tau _{\mathfrak {o},\mathfrak {c}^{-1}} {}^{*}(f_{\mathfrak {c}})\in \breve {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
, we obtain
$\tau _{\mathfrak {o},\mathfrak {c}^{-1}} {}^{*}(f_{\mathfrak {c}})\in \breve {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
, we obtain
 $F_{1}\in \breve {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
. Since
$F_{1}\in \breve {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
. Since
![]() $f_{\mathfrak {c}}$
is
$f_{\mathfrak {c}}$
is
![]() $\kappa ^{-1}$
-equivariant for the
$\kappa ^{-1}$
-equivariant for the
![]() $\mathbb {T}_{w}\left (\mathbb {Z}_{p}\right )$
-action, we have
$\mathbb {T}_{w}\left (\mathbb {Z}_{p}\right )$
-action, we have
![]() $F_{a}=\kappa \left (\hat {a}\right )F_{1}$
. Since the image of the character
$F_{a}=\kappa \left (\hat {a}\right )F_{1}$
. Since the image of the character
![]() $\kappa $
is contained in
$\kappa $
is contained in
 $\mathcal {O}_{\mathbb {C}_{p}}^{\times }$
, we see that
$\mathcal {O}_{\mathbb {C}_{p}}^{\times }$
, we see that
 $F_{a}\in \breve {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
for any
$F_{a}\in \breve {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
for any
![]() $a\in \mathbb {T}(\mathbb {Z}/p^{n}\mathbb {Z})$
. This means
$a\in \mathbb {T}(\mathbb {Z}/p^{n}\mathbb {Z})$
. This means
 $$ \begin{align} f_{\mathfrak{c}}\rvert_{\pi^{-1}_{w}\left(\breve{S}_{\sigma,\mathcal{O}_{\mathbb{C}_{p}}}\right)}\in \mathcal{O}\left(\pi_{w}^{-1}\left(\breve{S}_{\sigma,\mathcal{O}_{\mathbb{C}_{p}}}\right)\right). \end{align} $$
$$ \begin{align} f_{\mathfrak{c}}\rvert_{\pi^{-1}_{w}\left(\breve{S}_{\sigma,\mathcal{O}_{\mathbb{C}_{p}}}\right)}\in \mathcal{O}\left(\pi_{w}^{-1}\left(\breve{S}_{\sigma,\mathcal{O}_{\mathbb{C}_{p}}}\right)\right). \end{align} $$
To prove the proposition, we may assume
![]() $f_{\mathfrak {c}}\neq 0$
. Consider the ideal
$f_{\mathfrak {c}}\neq 0$
. Consider the ideal
 $J=\left \{x\in \mathcal {O}_{\mathbb {C}_{p}} \mid x f_{\mathfrak {c}} \in \mathbf {M}(\mu _{N},\mathfrak {c},\kappa )(0)\right \}$
, which is principal by Lemma 4.8(1). Put
$J=\left \{x\in \mathcal {O}_{\mathbb {C}_{p}} \mid x f_{\mathfrak {c}} \in \mathbf {M}(\mu _{N},\mathfrak {c},\kappa )(0)\right \}$
, which is principal by Lemma 4.8(1). Put
![]() $J=(x)$
and suppose
$J=(x)$
and suppose
![]() $x\in m_{\mathbb {C}_{p}}$
. Then the q-expansion
$x\in m_{\mathbb {C}_{p}}$
. Then the q-expansion
![]() $x f_{\mathfrak {c}}(q)$
is also integral, and zero modulo
$x f_{\mathfrak {c}}(q)$
is also integral, and zero modulo
![]() $m_{\mathbb {C}_{p}}$
. Thus the commutative diagram (4.11) and formula (4.12) imply that the pullback of
$m_{\mathbb {C}_{p}}$
. Thus the commutative diagram (4.11) and formula (4.12) imply that the pullback of
 $x f_{\mathfrak {c}}\in \mathbf {\Omega }^{\kappa }\left (\bar {\mathfrak {M}}^{\mathrm {ord}}_{\mathcal {O}_{\mathbb {C}_{p}}}\right )$
to
$x f_{\mathfrak {c}}\in \mathbf {\Omega }^{\kappa }\left (\bar {\mathfrak {M}}^{\mathrm {ord}}_{\mathcal {O}_{\mathbb {C}_{p}}}\right )$
to
 $i^{*}\mathbf {\Omega }^{\kappa }\rvert _{\hat {S}_{\mathscr {C},\bar {\mathbb {F}}_{p}}}\left (\hat {S}_{\mathscr {C},\bar {\mathbb {F}}_{p}}\right )$
vanishes.
$i^{*}\mathbf {\Omega }^{\kappa }\rvert _{\hat {S}_{\mathscr {C},\bar {\mathbb {F}}_{p}}}\left (\hat {S}_{\mathscr {C},\bar {\mathbb {F}}_{p}}\right )$
vanishes.
Note that the reduction of
 $\breve {S}_{\mathscr {C},\mathcal {O}_{\mathbb {C}_{p}}}\to \bar {\mathfrak {M}}^{\mathrm {ord}}_{\mathcal {O}_{\mathbb {C}_{p}}}$
induces the map on the special fiber
$\breve {S}_{\mathscr {C},\mathcal {O}_{\mathbb {C}_{p}}}\to \bar {\mathfrak {M}}^{\mathrm {ord}}_{\mathcal {O}_{\mathbb {C}_{p}}}$
induces the map on the special fiber
 $$ \begin{align*} \hat{S}_{\mathscr{C},\bar{\mathbb{F}}_{p}}=\left(\breve{S}_{\mathscr{C},\mathcal{O}_{\mathbb{C}_{p}}}\right)_{\bar{\mathbb{F}}_{p}} \to \bar{M}(\mu_{N},\mathfrak{c})_{\bar{\mathbb{F}}_{p}}. \end{align*} $$
$$ \begin{align*} \hat{S}_{\mathscr{C},\bar{\mathbb{F}}_{p}}=\left(\breve{S}_{\mathscr{C},\mathcal{O}_{\mathbb{C}_{p}}}\right)_{\bar{\mathbb{F}}_{p}} \to \bar{M}(\mu_{N},\mathfrak{c})_{\bar{\mathbb{F}}_{p}}. \end{align*} $$
Let
 $\bar {M}(\mu _{N},\mathfrak {c})_{\bar {\mathbb {F}}_{p}}\rvert ^{\wedge }_{D_{\bar {\mathbb {F}}_{p}}}$
be the formal completion of
$\bar {M}(\mu _{N},\mathfrak {c})_{\bar {\mathbb {F}}_{p}}\rvert ^{\wedge }_{D_{\bar {\mathbb {F}}_{p}}}$
be the formal completion of
 $\bar {M}(\mu _{N},\mathfrak {c})_{\bar {\mathbb {F}}_{p}}$
along its boundary
$\bar {M}(\mu _{N},\mathfrak {c})_{\bar {\mathbb {F}}_{p}}$
along its boundary
![]() $D_{\bar {\mathbb {F}}_{p}}$
. Recall that this map induces maps
$D_{\bar {\mathbb {F}}_{p}}$
. Recall that this map induces maps
 $$ \begin{align*} \hat{S}_{\mathscr{C},\bar{\mathbb{F}}_{p}} \to \hat{S}_{\mathscr{C},\bar{\mathbb{F}}_{p}}/U_{N} \to \bar{M}(\mu_{N},\mathfrak{c})_{\bar{\mathbb{F}}_{p}}\rvert^{\wedge}_{D_{\bar{\mathbb{F}}_{p}}}, \end{align*} $$
$$ \begin{align*} \hat{S}_{\mathscr{C},\bar{\mathbb{F}}_{p}} \to \hat{S}_{\mathscr{C},\bar{\mathbb{F}}_{p}}/U_{N} \to \bar{M}(\mu_{N},\mathfrak{c})_{\bar{\mathbb{F}}_{p}}\rvert^{\wedge}_{D_{\bar{\mathbb{F}}_{p}}}, \end{align*} $$
where the first arrow is a surjective local isomorphism and the second arrow is an open immersion. Hence
![]() $x f_{\mathfrak {c}}$
vanishes on a formal open subscheme of the formal completion
$x f_{\mathfrak {c}}$
vanishes on a formal open subscheme of the formal completion
 $\bar {M}(\mu _{N},\mathfrak {c})_{\bar {\mathbb {F}}_{p}}\rvert ^{\wedge }_{D_{\bar {\mathbb {F}}_{p}}}$
. We know that the smooth scheme
$\bar {M}(\mu _{N},\mathfrak {c})_{\bar {\mathbb {F}}_{p}}\rvert ^{\wedge }_{D_{\bar {\mathbb {F}}_{p}}}$
. We know that the smooth scheme
 $\bar {\mathfrak {M}}^{\mathrm {ord}}_{\bar {\mathbb {F}}_{p}}$
is irreducible. Since the sheaf
$\bar {\mathfrak {M}}^{\mathrm {ord}}_{\bar {\mathbb {F}}_{p}}$
is irreducible. Since the sheaf
![]() $\mathbf {\Omega }^{\kappa }$
is invertible on the ordinary locus, Krull’s intersection theorem implies that
$\mathbf {\Omega }^{\kappa }$
is invertible on the ordinary locus, Krull’s intersection theorem implies that
![]() $x f_{\mathfrak {c}}$
vanishes on a nonempty open subscheme of
$x f_{\mathfrak {c}}$
vanishes on a nonempty open subscheme of
 $\bar {\mathfrak {M}}^{\mathrm {ord}}_{\bar {\mathbb {F}}_{p}}$
, and thus it also vanishes on
$\bar {\mathfrak {M}}^{\mathrm {ord}}_{\bar {\mathbb {F}}_{p}}$
, and thus it also vanishes on
 $\bar {\mathfrak {M}}^{\mathrm {ord}}_{\bar {\mathbb {F}}_{p}}$
. Then Lemma 4.8(2) implies that
$\bar {\mathfrak {M}}^{\mathrm {ord}}_{\bar {\mathbb {F}}_{p}}$
. Then Lemma 4.8(2) implies that
![]() $x f_{\mathfrak {c}}\in y \mathbf {M}(\mu _{N},\mathfrak {c},\kappa )(0)$
for some
$x f_{\mathfrak {c}}\in y \mathbf {M}(\mu _{N},\mathfrak {c},\kappa )(0)$
for some
![]() $y\in m_{\mathbb {C}_{p}}$
. Since the
$y\in m_{\mathbb {C}_{p}}$
. Since the
![]() $\mathcal {O}_{\mathbb {C}_{p}}$
-module
$\mathcal {O}_{\mathbb {C}_{p}}$
-module
![]() $\mathbf {M}(\mu _{N},\mathfrak {c},\kappa )(0)$
is torsion free, this contradicts the choice of x. Thus we obtain
$\mathbf {M}(\mu _{N},\mathfrak {c},\kappa )(0)$
is torsion free, this contradicts the choice of x. Thus we obtain
 $x\in \mathcal {O}_{\mathbb {C}_{p}}^{\times }$
and
$x\in \mathcal {O}_{\mathbb {C}_{p}}^{\times }$
and
![]() $f_{\mathfrak {c}} \in \mathbf {M}(\mu _{N},\mathfrak {c},\kappa )(0)$
, which concludes the proof of the proposition.
$f_{\mathfrak {c}} \in \mathbf {M}(\mu _{N},\mathfrak {c},\kappa )(0)$
, which concludes the proof of the proposition.
Corollary 4.10. Let
 $f=(f_{\mathfrak {c}})_{\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{(p)}}$
be a nonzero eigenform in the space
$f=(f_{\mathfrak {c}})_{\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{(p)}}$
be a nonzero eigenform in the space
![]() $S^{G}(\mu _{N},(\nu ,w))(v)$
of weight
$S^{G}(\mu _{N},(\nu ,w))(v)$
of weight
![]() $(\nu ,w)\in \mathcal {W}^{G}\left (\mathbb {C}_{p}\right )$
. For any nonzero ideal
$(\nu ,w)\in \mathcal {W}^{G}\left (\mathbb {C}_{p}\right )$
. For any nonzero ideal
![]() $\mathfrak {n}$
of
$\mathfrak {n}$
of
![]() $\mathfrak {o}$
, the Hecke eigenvalue
$\mathfrak {o}$
, the Hecke eigenvalue
![]() $\Lambda (\mathfrak {n})$
is p-integral.
$\Lambda (\mathfrak {n})$
is p-integral.
Proof. By equation (3.8), it is enough to show the case where
![]() $\mathfrak {n}$
is a maximal ideal
$\mathfrak {n}$
is a maximal ideal
![]() $\mathfrak {m}$
. Put
$\mathfrak {m}$
. Put
![]() $\kappa =k(\nu ,w)$
. Note that by Lemmas 3.1 and 3.4, the restriction map
$\kappa =k(\nu ,w)$
. Note that by Lemmas 3.1 and 3.4, the restriction map
![]() $S^{G}(\mu _{N},(\nu ,w))(v)\to S^{G}(\mu _{N},(\nu ,w))(0)$
is injective. We consider
$S^{G}(\mu _{N},(\nu ,w))(v)\to S^{G}(\mu _{N},(\nu ,w))(0)$
is injective. We consider
![]() $\Lambda (\mathfrak {m})$
as an eigenvalue of the operator
$\Lambda (\mathfrak {m})$
as an eigenvalue of the operator
![]() $T_{\mathfrak {m}}$
acting on
$T_{\mathfrak {m}}$
acting on
 $$ \begin{align*} M:=\bigoplus_{\mathfrak{c}\in \left[\mathrm{Cl}^{+}(F)\right]^{\left(p\right)}} M(\mu_{N},\mathfrak{c},\kappa)(0). \end{align*} $$
$$ \begin{align*} M:=\bigoplus_{\mathfrak{c}\in \left[\mathrm{Cl}^{+}(F)\right]^{\left(p\right)}} M(\mu_{N},\mathfrak{c},\kappa)(0). \end{align*} $$
This is a Banach
![]() $\mathbb {C}_{p}$
-module with respect to the p-adic norm
$\mathbb {C}_{p}$
-module with respect to the p-adic norm
![]() $\lvert -\rvert $
defined by the
$\lvert -\rvert $
defined by the
![]() $\mathcal {O}_{\mathbb {C}_{p}}$
-lattice
$\mathcal {O}_{\mathbb {C}_{p}}$
-lattice
 $$ \begin{align*} \mathbf{M}:=\bigoplus_{\mathfrak{c}\in \left[\mathrm{Cl}^{+}(F)\right]^{\left(p\right)}} \mathbf{M}(\mu_{N},\mathfrak{c},\kappa)(0). \end{align*} $$
$$ \begin{align*} \mathbf{M}:=\bigoplus_{\mathfrak{c}\in \left[\mathrm{Cl}^{+}(F)\right]^{\left(p\right)}} \mathbf{M}(\mu_{N},\mathfrak{c},\kappa)(0). \end{align*} $$
Namely, we put
 $$ \begin{align*} \lvert f\rvert=\inf\left\{\lvert x\rvert^{-1}\mid x\in \mathbb{C}_{p}^{\times},\ xf\in \mathbf{M}\right\}. \end{align*} $$
$$ \begin{align*} \lvert f\rvert=\inf\left\{\lvert x\rvert^{-1}\mid x\in \mathbb{C}_{p}^{\times},\ xf\in \mathbf{M}\right\}. \end{align*} $$
By Lemma 4.8(1), we can find an element
![]() $x\in \mathbb {C}_{p}$
of largest absolute value satisfying
$x\in \mathbb {C}_{p}$
of largest absolute value satisfying
![]() $x f_{\mathfrak {c}}\in \mathbf {M}(\mu _{N},\mathfrak {c},\kappa )(0)$
for any
$x f_{\mathfrak {c}}\in \mathbf {M}(\mu _{N},\mathfrak {c},\kappa )(0)$
for any
 $\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
. The norm
$\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
. The norm
![]() $\lvert f\rvert $
is equal to
$\lvert f\rvert $
is equal to
![]() $\lvert x\rvert ^{-1}$
. Moreover, any coefficient of the q-expansion
$\lvert x\rvert ^{-1}$
. Moreover, any coefficient of the q-expansion
![]() $x f_{\mathfrak {c}}(q)$
is contained in
$x f_{\mathfrak {c}}(q)$
is contained in
![]() $\mathcal {O}_{\mathbb {C}_{p}}$
. By Lemma 4.6, so is
$\mathcal {O}_{\mathbb {C}_{p}}$
. By Lemma 4.6, so is
![]() $x T_{\mathfrak {m}} f$
. Hence Proposition 4.9 shows
$x T_{\mathfrak {m}} f$
. Hence Proposition 4.9 shows
![]() $x T_{\mathfrak {m}} f\in \mathbf {M}$
. This implies
$x T_{\mathfrak {m}} f\in \mathbf {M}$
. This implies
 $$ \begin{align*} \lvert\Lambda(\mathfrak{m})\rvert=\frac{\lvert T_{\mathfrak{m}} f\rvert}{\lvert f\rvert}\leq \frac{\lvert x\rvert^{-1}}{\lvert x\rvert^{-1}}=1, \end{align*} $$
$$ \begin{align*} \lvert\Lambda(\mathfrak{m})\rvert=\frac{\lvert T_{\mathfrak{m}} f\rvert}{\lvert f\rvert}\leq \frac{\lvert x\rvert^{-1}}{\lvert x\rvert^{-1}}=1, \end{align*} $$
and the corollary follows.
Corollary 4.11. Let
 $f=(f_{\mathfrak {c}})_{\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{\left (p\right )}}$
be a normalized eigenform in
$f=(f_{\mathfrak {c}})_{\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{\left (p\right )}}$
be a normalized eigenform in
![]() $S^{G}(\mu _{N},(\nu ,w))(v)$
of weight
$S^{G}(\mu _{N},(\nu ,w))(v)$
of weight
![]() $(\nu ,w)\in \mathcal {W}^{G}\left (\mathbb {C}_{p}\right )$
. Then we have
$(\nu ,w)\in \mathcal {W}^{G}\left (\mathbb {C}_{p}\right )$
. Then we have
for any
 $\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
and any
$\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
and any
 $\eta \in \left (\mathfrak {c}^{-1}\right )^{+}$
.
$\eta \in \left (\mathfrak {c}^{-1}\right )^{+}$
.
Corollary 4.12. Let
![]() $(\nu ,w)$
be an element of
$(\nu ,w)$
be an element of
![]() $\mathcal {W}^{G}\left (\mathbb {C}_{p}\right )$
.
$\mathcal {W}^{G}\left (\mathbb {C}_{p}\right )$
.
-
(1) For any
 $\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
, there exists an admissible affinoid open subset
$\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
, there exists an admissible affinoid open subset
 $\mathcal {S}_{\mathfrak {c}}\subseteq \bar {\mathcal {M}}(\mu _{N}, \mathfrak {c})(v)_{\mathbb {C}_{p}}$
such that
$\mathcal {S}_{\mathfrak {c}}\subseteq \bar {\mathcal {M}}(\mu _{N}, \mathfrak {c})(v)_{\mathbb {C}_{p}}$
such that
 $\left (\pi _{w}^{\mathrm {rig}}\right )^{-1}(\mathcal {S}_{\mathfrak {c}})$
meets every connected component of
$\left (\pi _{w}^{\mathrm {rig}}\right )^{-1}(\mathcal {S}_{\mathfrak {c}})$
meets every connected component of
 $\mathcal {IW}^{+}_{w,\mathfrak {c}}(v)_{\mathbb {C}_{p}}$
and, for any normalized eigenform
$\mathcal {IW}^{+}_{w,\mathfrak {c}}(v)_{\mathbb {C}_{p}}$
and, for any normalized eigenform
 $f=(f_{\mathfrak {c}})_{\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{\left (p\right )}}$
in
$f=(f_{\mathfrak {c}})_{\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{\left (p\right )}}$
in
 $S^{G}(\mu _{N},(\nu ,w))(v)$
, the restriction
$S^{G}(\mu _{N},(\nu ,w))(v)$
, the restriction
 $f_{\mathfrak {c}}\rvert _{\left (\pi _{w}^{\mathrm {rig}}\right )^{-1}\left (\mathcal {S}_{\mathfrak {c}}\right )}$
has absolute value bounded by
$f_{\mathfrak {c}}\rvert _{\left (\pi _{w}^{\mathrm {rig}}\right )^{-1}\left (\mathcal {S}_{\mathfrak {c}}\right )}$
has absolute value bounded by
 $1$
.
$1$
. -
(2) Let
 $f=(f_{\mathfrak {c}})_{\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{\left (p\right )}}$
be any element in the space
$f=(f_{\mathfrak {c}})_{\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{\left (p\right )}}$
be any element in the space
 $S^{G}(\mu _{N},(\nu ,w))(v)$
. If
$S^{G}(\mu _{N},(\nu ,w))(v)$
. If
 $f_{\mathfrak {c}}(q)=0$
for any
$f_{\mathfrak {c}}(q)=0$
for any
 $\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
, then
$\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
, then
 $f=0$
.
$f=0$
. -
(3) Let
 $f=(f_{\mathfrak {c}})_{\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{\left (p\right )}}$
and
$f=(f_{\mathfrak {c}})_{\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{\left (p\right )}}$
and
 $f^{\prime }=\left (f^{\prime }_{\mathfrak {c}}\right )_{\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{\left (p\right )}}$
be normalized eigenforms in
$f^{\prime }=\left (f^{\prime }_{\mathfrak {c}}\right )_{\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{\left (p\right )}}$
be normalized eigenforms in
 $S^{G}(\mu _{N},(\nu ,w))(v)$
. Suppose that the eigenvalues of the Hecke operator
$S^{G}(\mu _{N},(\nu ,w))(v)$
. Suppose that the eigenvalues of the Hecke operator
 $T_{\mathfrak {n}}$
acting on f and
$T_{\mathfrak {n}}$
acting on f and
 $f^{\prime }$
are the same for any nonzero ideal
$f^{\prime }$
are the same for any nonzero ideal
 $\mathfrak {n}\subseteq \mathfrak {o}$
. Then
$\mathfrak {n}\subseteq \mathfrak {o}$
. Then
 $f=f^{\prime }$
.
$f=f^{\prime }$
.
Proof. Let us prove the first assertion. For any
 $\sigma \in \mathscr {C}=\mathscr {C}\left (\mathfrak {o},\mathfrak {c}^{-1}\right )$
, Corollary 4.11 and formula (4.7) show that
$\sigma \in \mathscr {C}=\mathscr {C}\left (\mathfrak {o},\mathfrak {c}^{-1}\right )$
, Corollary 4.11 and formula (4.7) show that
 $\tau _{\mathfrak {o}, \mathfrak {c}^{-1}}^{*}(f_{\mathfrak {c}})$
is a rigid analytic function on
$\tau _{\mathfrak {o}, \mathfrak {c}^{-1}}^{*}(f_{\mathfrak {c}})$
is a rigid analytic function on
 $\breve {S}^{\mathrm {rig}}_{\sigma ,\mathbb {C}_{p}}$
with absolute value bounded by
$\breve {S}^{\mathrm {rig}}_{\sigma ,\mathbb {C}_{p}}$
with absolute value bounded by
![]() $1$
. As in the proof of Proposition 4.9, we can show that
$1$
. As in the proof of Proposition 4.9, we can show that
 $f_{\mathfrak {c}}\rvert _{\left (\pi _{w}^{\mathrm {rig}}\right )^{-1}\left (\breve {S}^{\mathrm {rig}}_{\mathscr {C},\mathbb {C}_{p}}\right )}$
is a rigid analytic function with absolute value bounded by
$f_{\mathfrak {c}}\rvert _{\left (\pi _{w}^{\mathrm {rig}}\right )^{-1}\left (\breve {S}^{\mathrm {rig}}_{\mathscr {C},\mathbb {C}_{p}}\right )}$
is a rigid analytic function with absolute value bounded by
![]() $1$
. Since the natural map
$1$
. Since the natural map
 $\breve {S}^{\mathrm {rig}}_{\mathscr {C},\mathbb {C}_{p}} \to \breve {S}_{\mathscr {C},\mathbb {C}_{p}}^{\mathrm {rig}}/U_{N}$
is a surjective local isomorphism, the restriction
$\breve {S}^{\mathrm {rig}}_{\mathscr {C},\mathbb {C}_{p}} \to \breve {S}_{\mathscr {C},\mathbb {C}_{p}}^{\mathrm {rig}}/U_{N}$
is a surjective local isomorphism, the restriction
 $f_{\mathfrak {c}}\rvert _{\left (\pi _{w}^{\mathrm {rig}}\right )^{-1} \left (\breve {S}_{\mathscr {C},\mathbb {C}_{p}}^{\mathrm {rig}}/U_{N}\right )}$
is also, with absolute value bounded by
$f_{\mathfrak {c}}\rvert _{\left (\pi _{w}^{\mathrm {rig}}\right )^{-1} \left (\breve {S}_{\mathscr {C},\mathbb {C}_{p}}^{\mathrm {rig}}/U_{N}\right )}$
is also, with absolute value bounded by
![]() $1$
. Thus, for any nonempty admissible affinoid open subset
$1$
. Thus, for any nonempty admissible affinoid open subset
 $\mathcal {S}_{\mathfrak {c}}\subseteq \breve {S}_{\mathscr {C},\mathbb {C}_{p}}^{\mathrm {rig}}/U_{N}$
, the absolute value of
$\mathcal {S}_{\mathfrak {c}}\subseteq \breve {S}_{\mathscr {C},\mathbb {C}_{p}}^{\mathrm {rig}}/U_{N}$
, the absolute value of
 $f_{\mathfrak {c}}\rvert _{\left (\pi _{w}^{\mathrm {rig}}\right )^{-1}\left (\mathcal {S}_{\mathfrak {c}}\right )}$
is bounded by
$f_{\mathfrak {c}}\rvert _{\left (\pi _{w}^{\mathrm {rig}}\right )^{-1}\left (\mathcal {S}_{\mathfrak {c}}\right )}$
is bounded by
![]() $1$
. Since
$1$
. Since
 $\breve {S}_{\mathscr {C},\mathbb {C}_{p}}^{\mathrm {rig}}/U_{N}$
is an admissible open subset of
$\breve {S}_{\mathscr {C},\mathbb {C}_{p}}^{\mathrm {rig}}/U_{N}$
is an admissible open subset of
![]() $\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})(v)_{\mathbb {C}_{p}}$
, we see that
$\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})(v)_{\mathbb {C}_{p}}$
, we see that
![]() $\mathcal {S}_{\mathfrak {c}}$
is also its admissible open subset.
$\mathcal {S}_{\mathfrak {c}}$
is also its admissible open subset.
On the other hand, the rigid analytic variety
![]() $\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})(v)_{\mathbb {C}_{p}}$
is connected by Lemma 3.4. Since the map
$\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})(v)_{\mathbb {C}_{p}}$
is connected by Lemma 3.4. Since the map
 $$ \begin{align*} h^{\mathrm{rig}}_{n}: \bar{\mathcal{M}}(\Gamma_{1}(p^{n}),\mu_{N},\mathfrak{c})(v)_{\mathbb{C}_{p}}\to \bar{\mathcal{M}}(\mu_{N},\mathfrak{c})(v)_{\mathbb{C}_{p}} \end{align*} $$
$$ \begin{align*} h^{\mathrm{rig}}_{n}: \bar{\mathcal{M}}(\Gamma_{1}(p^{n}),\mu_{N},\mathfrak{c})(v)_{\mathbb{C}_{p}}\to \bar{\mathcal{M}}(\mu_{N},\mathfrak{c})(v)_{\mathbb{C}_{p}} \end{align*} $$
is finite and étale [Reference Conrad18, Theorem A.2.4], it is surjective on each connected component of the rigid analytic variety
![]() $\bar {\mathcal {M}}(\Gamma _{1}(p^{n}),\mu _{N}, \mathfrak {c})(v)_{\mathbb {C}_{p}}$
, and thus
$\bar {\mathcal {M}}(\Gamma _{1}(p^{n}),\mu _{N}, \mathfrak {c})(v)_{\mathbb {C}_{p}}$
, and thus
 $\left (h_{n}^{\mathrm {rig}}\right )^{-1}(\mathcal {S}_{\mathfrak {c}})$
meets every connected component of it.
$\left (h_{n}^{\mathrm {rig}}\right )^{-1}(\mathcal {S}_{\mathfrak {c}})$
meets every connected component of it.
We claim that the map
 $$ \begin{align*} \gamma_{w}^{\mathrm{rig}}: \mathcal{IW}_{w,\mathfrak{c}}^{+}(v)_{\mathbb{C}_{p}}\to \bar{\mathcal{M}}(\Gamma_{1}(p^{n}),\mu_{N},\mathfrak{c})(v)_{\mathbb{C}_{p}} \end{align*} $$
$$ \begin{align*} \gamma_{w}^{\mathrm{rig}}: \mathcal{IW}_{w,\mathfrak{c}}^{+}(v)_{\mathbb{C}_{p}}\to \bar{\mathcal{M}}(\Gamma_{1}(p^{n}),\mu_{N},\mathfrak{c})(v)_{\mathbb{C}_{p}} \end{align*} $$
induces a bijection
 $$ \begin{align*} \pi_{0}\left(\mathcal{IW}_{w,\mathfrak{c}}^{+}(v)_{\mathbb{C}_{p}}\right)\to \pi_{0}\left(\bar{\mathcal{M}}(\Gamma_{1}(p^{n}),\mu_{N},\mathfrak{c})(v)_{\mathbb{C}_{p}}\right) \end{align*} $$
$$ \begin{align*} \pi_{0}\left(\mathcal{IW}_{w,\mathfrak{c}}^{+}(v)_{\mathbb{C}_{p}}\right)\to \pi_{0}\left(\bar{\mathcal{M}}(\Gamma_{1}(p^{n}),\mu_{N},\mathfrak{c})(v)_{\mathbb{C}_{p}}\right) \end{align*} $$
between the sets of connected components. Indeed, by [Reference Conrad17, Corollary 3.2.3], it is enough to show the claim with
![]() $\mathbb {C}_{p}$
replaced by a finite extension
$\mathbb {C}_{p}$
replaced by a finite extension
![]() $L/K$
. By a finite base extension, we may assume
$L/K$
. By a finite base extension, we may assume
![]() $L=K$
. Since the formal schemes
$L=K$
. Since the formal schemes
 $ \mathfrak {IW}_{w,\mathfrak {c}}^{+}(v)$
and
$ \mathfrak {IW}_{w,\mathfrak {c}}^{+}(v)$
and
![]() $\bar {\mathfrak {M}}(\Gamma _{1}(p^{n}),\mu _{N},\mathfrak {c})(v)$
are both normal, it is enough to show a similar assertion for the formal model
$\bar {\mathfrak {M}}(\Gamma _{1}(p^{n}),\mu _{N},\mathfrak {c})(v)$
are both normal, it is enough to show a similar assertion for the formal model
![]() $\gamma _{w}$
. Since it is a formal
$\gamma _{w}$
. Since it is a formal
![]() $\mathbb {T}^{0}_{w}$
-torsor, it is surjective and the map between the sets of connected components is also surjective. Let
$\mathbb {T}^{0}_{w}$
-torsor, it is surjective and the map between the sets of connected components is also surjective. Let
![]() $\mathfrak {Y}$
be any connected component of
$\mathfrak {Y}$
be any connected component of
![]() $\bar {\mathfrak {M}}(\Gamma _{1}(p^{n}),\mu _{N},\mathfrak {c})(v)$
and let
$\bar {\mathfrak {M}}(\Gamma _{1}(p^{n}),\mu _{N},\mathfrak {c})(v)$
and let
 $\left \{\mathfrak {X}_{j}\right \}_{j\in J}$
be the set of connected components of
$\left \{\mathfrak {X}_{j}\right \}_{j\in J}$
be the set of connected components of
 $\mathfrak {IW}_{w,\mathfrak {c}}^{+}(v)$
which
$\mathfrak {IW}_{w,\mathfrak {c}}^{+}(v)$
which
![]() $ \gamma _{w}$
maps to
$ \gamma _{w}$
maps to
![]() $\mathfrak {Y}$
. Suppose
$\mathfrak {Y}$
. Suppose
![]() $\sharp J\geq 2$
. Since
$\sharp J\geq 2$
. Since
![]() $\gamma _{w}$
is finitely presented and flat, it is open and the connectedness of
$\gamma _{w}$
is finitely presented and flat, it is open and the connectedness of
![]() $\mathfrak {Y}$
implies that
$\mathfrak {Y}$
implies that
![]() $ \gamma _{w}\left (\mathfrak {X}_{j}\right )\cap \gamma _{w}\left (\mathfrak {X}_{j^{\prime }}\right )\neq \emptyset $
for some
$ \gamma _{w}\left (\mathfrak {X}_{j}\right )\cap \gamma _{w}\left (\mathfrak {X}_{j^{\prime }}\right )\neq \emptyset $
for some
![]() $j\neq j^{\prime }$
. However, for any element y of this intersection, the fiber
$j\neq j^{\prime }$
. However, for any element y of this intersection, the fiber
![]() $\gamma _{w}^{-1}(y)$
is connected, since it is isomorphic to the special fiber of
$\gamma _{w}^{-1}(y)$
is connected, since it is isomorphic to the special fiber of
![]() $\mathbb {T}^{0}_{w}$
, which is a contradiction. Since
$\mathbb {T}^{0}_{w}$
, which is a contradiction. Since
![]() $\gamma _{w}^{\mathrm {rig}}$
is surjective, the claim shows that every connected component of
$\gamma _{w}^{\mathrm {rig}}$
is surjective, the claim shows that every connected component of
 $\mathcal {IW}^{+}_{w,\mathfrak {c}}(v)_{\mathbb {C}_{p}}$
meets the admissible open subset
$\mathcal {IW}^{+}_{w,\mathfrak {c}}(v)_{\mathbb {C}_{p}}$
meets the admissible open subset
 $\left (\pi _{w}^{\mathrm {rig}}\right )^{-1}(\mathcal {S}_{\mathfrak {c}})$
, and the first assertion follows.
$\left (\pi _{w}^{\mathrm {rig}}\right )^{-1}(\mathcal {S}_{\mathfrak {c}})$
, and the first assertion follows.
Now suppose that
![]() $f_{\mathfrak {c}}(q)=0$
for any
$f_{\mathfrak {c}}(q)=0$
for any
 $\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
. Then we have
$\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
. Then we have
 $f_{\mathfrak {c}}\rvert _{\left (\pi _{w}^{\mathrm {rig}}\right )^{-1}\left (\mathcal {S}_{\mathfrak {c}}\right )}=0$
. Since the rigid analytic variety
$f_{\mathfrak {c}}\rvert _{\left (\pi _{w}^{\mathrm {rig}}\right )^{-1}\left (\mathcal {S}_{\mathfrak {c}}\right )}=0$
. Since the rigid analytic variety
 $\mathcal {IW}^{+}_{w,\mathfrak {c}}(v)_{\mathbb {C}_{p}}$
is smooth over
$\mathcal {IW}^{+}_{w,\mathfrak {c}}(v)_{\mathbb {C}_{p}}$
is smooth over
![]() $\mathbb {C}_{p}$
, the first assertion and Lemma 3.1 show the second assertion. The third assertion follows from Proposition 4.7 and the second one.
$\mathbb {C}_{p}$
, the first assertion and Lemma 3.1 show the second assertion. The third assertion follows from Proposition 4.7 and the second one.
4.4 Normalized overconvergent modular forms in families
Let
![]() $\mathcal {U}=\mathrm {Sp}(A)$
be a smooth
$\mathcal {U}=\mathrm {Sp}(A)$
be a smooth
![]() $\mathbb {C}_{p}$
-affinoid variety and put
$\mathbb {C}_{p}$
-affinoid variety and put
![]() $\mathfrak {U}=\mathrm {Spf}(A^{\circ })$
. Let
$\mathfrak {U}=\mathrm {Spf}(A^{\circ })$
. Let
 $\mathcal {U}\to \mathcal {W}^{G}_{\mathbb {C}_{p}}$
be an n-analytic morphism and consider the associated weight characters
$\mathcal {U}\to \mathcal {W}^{G}_{\mathbb {C}_{p}}$
be an n-analytic morphism and consider the associated weight characters
 $\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )$
as before. Let
$\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )$
as before. Let
 $f=(f_{\mathfrak {c}})_{\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{\left (p\right )}}$
be an eigenform in the space
$f=(f_{\mathfrak {c}})_{\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{\left (p\right )}}$
be an eigenform in the space
 $S^{G}\left (\mu _{N}, \left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )(v)$
. Recall that each
$S^{G}\left (\mu _{N}, \left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )(v)$
. Recall that each
![]() $f_{\mathfrak {c}}$
is an element of
$f_{\mathfrak {c}}$
is an element of
 $\mathcal {O}\left (\mathfrak {IW}_{w,\mathfrak {c}}^{+}(v)_{\mathcal {O}_{\mathbb {C}_{p}}}\times \mathfrak {U}\right )[1/p]$
. For the cusp
$\mathcal {O}\left (\mathfrak {IW}_{w,\mathfrak {c}}^{+}(v)_{\mathcal {O}_{\mathbb {C}_{p}}}\times \mathfrak {U}\right )[1/p]$
. For the cusp
 $\left (\mathfrak {o},\mathfrak {c}^{-1},\mathrm {id}\right )$
of
$\left (\mathfrak {o},\mathfrak {c}^{-1},\mathrm {id}\right )$
of
![]() $M(\mu _{N},\mathfrak {c})$
and any
$M(\mu _{N},\mathfrak {c})$
and any
 $\sigma \in \mathscr {C}=\mathscr {C}\left (\mathfrak {o},\mathfrak {c}^{-1}\right )$
, we have the map
$\sigma \in \mathscr {C}=\mathscr {C}\left (\mathfrak {o},\mathfrak {c}^{-1}\right )$
, we have the map
 $$ \begin{align*} \tau_{\mathfrak{o},\mathfrak{c}^{-1}}\times 1: \breve{S}_{\sigma,\mathcal{O}_{\mathbb{C}_{p}}} \times \mathfrak{U} \to \mathfrak{IW}_{w,\mathfrak{c}}^{+}(v)_{\mathcal{O}_{\mathbb{C}_{p}}}\times \mathfrak{U} \end{align*} $$
$$ \begin{align*} \tau_{\mathfrak{o},\mathfrak{c}^{-1}}\times 1: \breve{S}_{\sigma,\mathcal{O}_{\mathbb{C}_{p}}} \times \mathfrak{U} \to \mathfrak{IW}_{w,\mathfrak{c}}^{+}(v)_{\mathcal{O}_{\mathbb{C}_{p}}}\times \mathfrak{U} \end{align*} $$
over
 $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(v)_{\mathcal {O}_{\mathbb {C}_{p}}}\times \mathfrak {U}$
.
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(v)_{\mathcal {O}_{\mathbb {C}_{p}}}\times \mathfrak {U}$
.
As in §4.1, we see that the ring
 $\breve {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}\hat {\otimes }_{\mathcal {O}_{\mathbb {C}_{p}}}A^{\circ }$
is isomorphic to the completion of the ring
$\breve {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}\hat {\otimes }_{\mathcal {O}_{\mathbb {C}_{p}}}A^{\circ }$
is isomorphic to the completion of the ring
 $$ \begin{align*} A^{\circ}\left[q^{\xi_{1}},\dotsc, q^{\xi_{r}}\right]\left[q^{\pm \xi_{r+1}},\dotsc, q^{\pm \xi_{g}}\right] \end{align*} $$
$$ \begin{align*} A^{\circ}\left[q^{\xi_{1}},\dotsc, q^{\xi_{r}}\right]\left[q^{\pm \xi_{r+1}},\dotsc, q^{\pm \xi_{g}}\right] \end{align*} $$
with respect to the
 $\left (p, q^{\xi _{1}}\dotsm q^{\xi _{r}}\right )$
-adic topology for some
$\left (p, q^{\xi _{1}}\dotsm q^{\xi _{r}}\right )$
-adic topology for some
![]() $\xi _{1},\dotsc ,\xi _{g}\in \mathfrak {c}^{-1}\cap \sigma ^{\vee }$
, and thus it can be considered as a subring of the ring
$\xi _{1},\dotsc ,\xi _{g}\in \mathfrak {c}^{-1}\cap \sigma ^{\vee }$
, and thus it can be considered as a subring of the ring
 $$ \begin{align*} A^{\circ}\left\langle q^{\pm \xi_{r+1}},\dotsc, q^{\pm \xi_{g}}\right\rangle \left[\left[q^{\xi_{1}},\dotsc, q^{\xi_{r}}\right]\right]. \end{align*} $$
$$ \begin{align*} A^{\circ}\left\langle q^{\pm \xi_{r+1}},\dotsc, q^{\pm \xi_{g}}\right\rangle \left[\left[q^{\xi_{1}},\dotsc, q^{\xi_{r}}\right]\right]. \end{align*} $$
Hence we obtain the map of the
![]() $q^{1}$
-coefficient
$q^{1}$
-coefficient
 $$ \begin{align*} \mathrm{pr}_{q^{1}}^{\mathcal{U}}: \mathcal{O}\left(\breve{S}_{\sigma,\mathcal{O}_{\mathbb{C}_{p}}}\times \mathfrak{U}\right)[1/p]\to A. \end{align*} $$
$$ \begin{align*} \mathrm{pr}_{q^{1}}^{\mathcal{U}}: \mathcal{O}\left(\breve{S}_{\sigma,\mathcal{O}_{\mathbb{C}_{p}}}\times \mathfrak{U}\right)[1/p]\to A. \end{align*} $$
For any eigenform
 $f\in S^{G}\left (\mu _{N},\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )(v)$
as before, we put
$f\in S^{G}\left (\mu _{N},\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )(v)$
as before, we put
 $a_{\mathfrak {o},\mathfrak {o}}^{\mathcal {U}}(f,1)=\mathrm {pr}_{q^{1}}^{\mathcal {U}}((\tau _{\mathfrak {o},\mathfrak {o}}\times 1)^{*}(f_{\mathfrak {o}}))\in A$
.
$a_{\mathfrak {o},\mathfrak {o}}^{\mathcal {U}}(f,1)=\mathrm {pr}_{q^{1}}^{\mathcal {U}}((\tau _{\mathfrak {o},\mathfrak {o}}\times 1)^{*}(f_{\mathfrak {o}}))\in A$
.
For any
![]() $x\in \mathcal {U}\left (\mathbb {C}_{p}\right )$
, put
$x\in \mathcal {U}\left (\mathbb {C}_{p}\right )$
, put
 $(\nu ,w)=\left (\nu ^{\mathcal {U}}(x),w^{\mathcal {U}}(x)\right )$
. The specialization
$(\nu ,w)=\left (\nu ^{\mathcal {U}}(x),w^{\mathcal {U}}(x)\right )$
. The specialization
 $f(x)=(f_{\mathfrak {c}}(x))_{\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{\left (p\right )}}$
is an element of the space
$f(x)=(f_{\mathfrak {c}}(x))_{\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{\left (p\right )}}$
is an element of the space
![]() $S^{G}(\mu _{N},(\nu ,w))(v)$
over
$S^{G}(\mu _{N},(\nu ,w))(v)$
over
![]() $\mathbb {C}_{p}$
, and we have the usual
$\mathbb {C}_{p}$
, and we have the usual
![]() $q^{1}$
-coefficient
$q^{1}$
-coefficient
![]() $a_{\mathfrak {o},\mathfrak {o}}(f(x),1)$
of the q-expansion of
$a_{\mathfrak {o},\mathfrak {o}}(f(x),1)$
of the q-expansion of
![]() $f(x)$
. By the commutative diagram
$f(x)$
. By the commutative diagram

we obtain
 $$ \begin{align} a_{\mathfrak{o},\mathfrak{o}}^{\mathcal{U}}(f,1)(x)=a_{\mathfrak{o},\mathfrak{o}}(f(x),1). \end{align} $$
$$ \begin{align} a_{\mathfrak{o},\mathfrak{o}}^{\mathcal{U}}(f,1)(x)=a_{\mathfrak{o},\mathfrak{o}}(f(x),1). \end{align} $$
Lemma 4.13. Suppose that
![]() $f(x)\neq 0$
for any
$f(x)\neq 0$
for any
![]() $x\in \mathcal {U}\left (\mathbb {C}_{p}\right )$
. Then we have
$x\in \mathcal {U}\left (\mathbb {C}_{p}\right )$
. Then we have
 $$ \begin{align*} a_{\mathfrak{o},\mathfrak{o}}^{\mathcal{U}}(f,1)\in A^{\times}. \end{align*} $$
$$ \begin{align*} a_{\mathfrak{o},\mathfrak{o}}^{\mathcal{U}}(f,1)\in A^{\times}. \end{align*} $$
In particular, the specialization
![]() $f^{\prime }(x)$
of
$f^{\prime }(x)$
of
 $f^{\prime }=a_{\mathfrak {o},\mathfrak {o}}^{\mathcal {U}}(f,1)^{-1} f$
is a normalized eigenform with the same eigenvalues as
$f^{\prime }=a_{\mathfrak {o},\mathfrak {o}}^{\mathcal {U}}(f,1)^{-1} f$
is a normalized eigenform with the same eigenvalues as
![]() $f(x)$
for any
$f(x)$
for any
![]() $x\in \mathcal {U}\left (\mathbb {C}_{p}\right )$
.
$x\in \mathcal {U}\left (\mathbb {C}_{p}\right )$
.
Proof. We claim that
![]() $a_{\mathfrak {o},\mathfrak {o}}(f(x),1)\neq 0$
for any
$a_{\mathfrak {o},\mathfrak {o}}(f(x),1)\neq 0$
for any
![]() $x\in \mathcal {U}\left (\mathbb {C}_{p}\right )$
. Indeed, suppose that
$x\in \mathcal {U}\left (\mathbb {C}_{p}\right )$
. Indeed, suppose that
![]() $a_{\mathfrak {o},\mathfrak {o}}(f(x),1)=0$
for some
$a_{\mathfrak {o},\mathfrak {o}}(f(x),1)=0$
for some
![]() $x\in \mathcal {U}\left (\mathbb {C}_{p}\right )$
. Since
$x\in \mathcal {U}\left (\mathbb {C}_{p}\right )$
. Since
![]() $f(x)$
is an eigenform, Proposition 4.7 implies that the q-expansion
$f(x)$
is an eigenform, Proposition 4.7 implies that the q-expansion
![]() $f(x)_{\mathfrak {c}}(q)$
of
$f(x)_{\mathfrak {c}}(q)$
of
![]() $f(x)$
is zero for any
$f(x)$
is zero for any
 $\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
. By Corollary 4.12(2) we have
$\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
. By Corollary 4.12(2) we have
![]() $f(x)=0$
, which is a contradiction.
$f(x)=0$
, which is a contradiction.
Now equation (4.13) implies that
 $a_{\mathfrak {o},\mathfrak {o}}^{\mathcal {U}}(f,1)(x)\neq 0$
for any
$a_{\mathfrak {o},\mathfrak {o}}^{\mathcal {U}}(f,1)(x)\neq 0$
for any
![]() $x\in \mathcal {U}\left (\mathbb {C}_{p}\right )$
. Hence we obtain
$x\in \mathcal {U}\left (\mathbb {C}_{p}\right )$
. Hence we obtain
 $a_{\mathfrak {o},\mathfrak {o}}^{\mathcal {U}}(f,1)\in A^{\times }$
.
$a_{\mathfrak {o},\mathfrak {o}}^{\mathcal {U}}(f,1)\in A^{\times }$
.
4.5 Gluing results
Here we prove two results on gluing overconvergent Hilbert modular forms, based on the theory of the q-expansion developed in the foregoing. Let
![]() $\mathcal {X}=\mathrm {Sp}(R)$
be any admissible affinoid open subset of
$\mathcal {X}=\mathrm {Sp}(R)$
be any admissible affinoid open subset of
![]() $\mathcal {W}^{G}$
. Put
$\mathcal {W}^{G}$
. Put
![]() $n=n(\mathcal {X})$
and
$n=n(\mathcal {X})$
and
![]() $v=v_{n}$
as in §3.3.3. Consider the Hilbert eigenvariety
$v=v_{n}$
as in §3.3.3. Consider the Hilbert eigenvariety
![]() $\mathcal {E}\rvert _{\mathcal {X}}\to \mathcal {X}$
, which is constructed from the input data
$\mathcal {E}\rvert _{\mathcal {X}}\to \mathcal {X}$
, which is constructed from the input data
 $$ \begin{align*} \left(R,S^{G}\left(\mu_{N},\left(\nu^{\mathcal{X}},w^{\mathcal{X}}\right)\right)(v_{\mathrm{tot}}),\mathbf{T},U_{p}\right). \end{align*} $$
$$ \begin{align*} \left(R,S^{G}\left(\mu_{N},\left(\nu^{\mathcal{X}},w^{\mathcal{X}}\right)\right)(v_{\mathrm{tot}}),\mathbf{T},U_{p}\right). \end{align*} $$
4.5.1 Gluing local eigenforms
Lemma 4.14. Let
![]() $\mathcal {U}=\mathrm {Sp}(A)$
be a smooth
$\mathcal {U}=\mathrm {Sp}(A)$
be a smooth
![]() $\mathbb {C}_{p}$
-affinoid variety and let
$\mathbb {C}_{p}$
-affinoid variety and let
![]() $\mathcal {U}\to \mathcal {X}_{\mathbb {C}_{p}}$
be a morphism of rigid analytic varieties over
$\mathcal {U}\to \mathcal {X}_{\mathbb {C}_{p}}$
be a morphism of rigid analytic varieties over
![]() $\mathbb {C}_{p}$
. Let f be an eigenvector of the space
$\mathbb {C}_{p}$
. Let f be an eigenvector of the space
 $S^{G}\left (\mu _{N},\left (\nu ^{\mathcal {X}},w^{\mathcal {X}}\right )\right )(v_{\mathrm {tot}})\hat {\otimes }_{R} A$
for the action of
$S^{G}\left (\mu _{N},\left (\nu ^{\mathcal {X}},w^{\mathcal {X}}\right )\right )(v_{\mathrm {tot}})\hat {\otimes }_{R} A$
for the action of
![]() $\mathbf {T}$
such that for any
$\mathbf {T}$
such that for any
![]() $x\in \mathcal {U}\left (\mathbb {C}_{p}\right )$
, the specialization
$x\in \mathcal {U}\left (\mathbb {C}_{p}\right )$
, the specialization
 $$ \begin{align*} f(x)\in S^{G}\left(\mu_{N},\left(\nu^{\mathcal{X}},w^{\mathcal{X}}\right)\right)(v_{\mathrm{tot}})\hat{\otimes}_{R,x^{*}} \mathbb{C}_{p} \end{align*} $$
$$ \begin{align*} f(x)\in S^{G}\left(\mu_{N},\left(\nu^{\mathcal{X}},w^{\mathcal{X}}\right)\right)(v_{\mathrm{tot}})\hat{\otimes}_{R,x^{*}} \mathbb{C}_{p} \end{align*} $$
is nonzero. Then the image of f by the natural map
 $$ \begin{align*} S^{G}\left(\mu_{N},\left(\nu^{\mathcal{X}},w^{\mathcal{X}}\right)\right)(v_{\mathrm{tot}})\hat{\otimes}_{R} A\to S^{G}\left(\mu_{N},\left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)(v_{\mathrm{tot}}) \end{align*} $$
$$ \begin{align*} S^{G}\left(\mu_{N},\left(\nu^{\mathcal{X}},w^{\mathcal{X}}\right)\right)(v_{\mathrm{tot}})\hat{\otimes}_{R} A\to S^{G}\left(\mu_{N},\left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)(v_{\mathrm{tot}}) \end{align*} $$
is an eigenform with the same property.
Proof. Put
 $(\nu ,w)=\left (\nu ^{\mathcal {U}}(x),w^{\mathcal {U}}(x)\right )$
. Then we have the commutative diagram
$(\nu ,w)=\left (\nu ^{\mathcal {U}}(x),w^{\mathcal {U}}(x)\right )$
. Then we have the commutative diagram

Here the lowest two arrows are the specialization maps. Since
![]() $\mathcal {W}^{G}$
is smooth, the maximal ideal of
$\mathcal {W}^{G}$
is smooth, the maximal ideal of
![]() $R\hat {\otimes }_{K}\mathbb {C}_{p}$
corresponding to x is generated by a regular sequence. By Lemma 3.13, the left oblique arrow is an isomorphism. This implies the lemma.
$R\hat {\otimes }_{K}\mathbb {C}_{p}$
corresponding to x is generated by a regular sequence. By Lemma 3.13, the left oblique arrow is an isomorphism. This implies the lemma.
Proposition 4.15. Let
![]() $\mathcal {Z}$
be a smooth rigid analytic variety over
$\mathcal {Z}$
be a smooth rigid analytic variety over
![]() $\mathbb {C}_{p}$
which is principally refined. Let
$\mathbb {C}_{p}$
which is principally refined. Let
![]() $\varphi :\mathcal {Z}\to (\mathcal {E}\rvert _{\mathcal {X}})_{\mathbb {C}_{p}}$
be a morphism of rigid analytic varieties over
$\varphi :\mathcal {Z}\to (\mathcal {E}\rvert _{\mathcal {X}})_{\mathbb {C}_{p}}$
be a morphism of rigid analytic varieties over
![]() $\mathbb {C}_{p}$
. Then there exist an element
$\mathbb {C}_{p}$
. Then there exist an element
 $$ \begin{align*} f\in \bigoplus_{\mathfrak{c}\in \left[\mathrm{Cl}^{+}(F)\right]^{\left(p\right)}} \mathcal{O}\left(\mathcal{IW}_{w,\mathfrak{c}}^{+}(v_{\mathrm{tot}})_{\mathbb{C}_{p}}\times \mathcal{Z}\right) \end{align*} $$
$$ \begin{align*} f\in \bigoplus_{\mathfrak{c}\in \left[\mathrm{Cl}^{+}(F)\right]^{\left(p\right)}} \mathcal{O}\left(\mathcal{IW}_{w,\mathfrak{c}}^{+}(v_{\mathrm{tot}})_{\mathbb{C}_{p}}\times \mathcal{Z}\right) \end{align*} $$
and an admissible affinoid covering
![]() $\mathcal {Z}=\bigcup _{i\in I} \mathcal {U}_{i}$
such that the restriction
$\mathcal {Z}=\bigcup _{i\in I} \mathcal {U}_{i}$
such that the restriction
![]() $f\rvert _{\mathcal {U}_{i}}$
for each
$f\rvert _{\mathcal {U}_{i}}$
for each
![]() $i\in I$
is an eigenform of
$i\in I$
is an eigenform of
 $S^{G}\left (\mu _{N}, \left (\nu ^{\mathcal {U}_{i}},w^{\mathcal {U}_{i}}\right )\right )(v_{\mathrm {tot}})$
with eigensystem
$S^{G}\left (\mu _{N}, \left (\nu ^{\mathcal {U}_{i}},w^{\mathcal {U}_{i}}\right )\right )(v_{\mathrm {tot}})$
with eigensystem
![]() $\varphi ^{*}: \mathbf {T}\to \mathcal {O}(\mathcal {Z})\to \mathcal {O}(\mathcal {U}_{i})$
and
$\varphi ^{*}: \mathbf {T}\to \mathcal {O}(\mathcal {Z})\to \mathcal {O}(\mathcal {U}_{i})$
and
![]() $f(z)$
is normalized for any
$f(z)$
is normalized for any
![]() $z\in \mathcal {Z}$
.
$z\in \mathcal {Z}$
.
Proof. By Proposition 2.5(2), there exist an admissible affinoid covering
![]() $\mathcal {Z}=\bigcup _{i\in I} \mathcal {U}_{i}$
,
$\mathcal {Z}=\bigcup _{i\in I} \mathcal {U}_{i}$
,
![]() $\mathcal {U}_{i}=\mathrm {Sp}(A_{i})$
with a principal ideal domain
$\mathcal {U}_{i}=\mathrm {Sp}(A_{i})$
with a principal ideal domain
![]() $A_{i}$
, and an eigenvector
$A_{i}$
, and an eigenvector
![]() $f_{i}$
in the space
$f_{i}$
in the space
 $$ \begin{align*} S^{G}\left(\mu_{N},\left(\nu^{\mathcal{X}},w^{\mathcal{X}}\right)\right)(v_{\mathrm{tot}})\hat{\otimes}_{R} A_{i} \end{align*} $$
$$ \begin{align*} S^{G}\left(\mu_{N},\left(\nu^{\mathcal{X}},w^{\mathcal{X}}\right)\right)(v_{\mathrm{tot}})\hat{\otimes}_{R} A_{i} \end{align*} $$
such that for any
![]() $z\in \mathcal {U}_{i}$
, we have
$z\in \mathcal {U}_{i}$
, we have
![]() $f_{i}(z)\neq 0$
and
$f_{i}(z)\neq 0$
and
for any
![]() $h\in \mathbf {T}$
. By Lemma 4.14, the image
$h\in \mathbf {T}$
. By Lemma 4.14, the image
![]() $f^{\prime }_{i}$
of
$f^{\prime }_{i}$
of
![]() $f_{i}$
in the space
$f_{i}$
in the space
 $S^{G}\left (\mu _{N},\left (\nu ^{\mathcal {U}_{i}},w^{\mathcal {U}_{i}}\right )\right )(v_{\mathrm {tot}})$
is an eigenform with eigensystem
$S^{G}\left (\mu _{N},\left (\nu ^{\mathcal {U}_{i}},w^{\mathcal {U}_{i}}\right )\right )(v_{\mathrm {tot}})$
is an eigenform with eigensystem
![]() $\varphi ^{*}:\mathbf {T}\to A_{i}$
such that
$\varphi ^{*}:\mathbf {T}\to A_{i}$
such that
![]() $f^{\prime }_{i}(z)\neq 0$
for any
$f^{\prime }_{i}(z)\neq 0$
for any
![]() $z\in \mathcal {U}_{i}$
. Since
$z\in \mathcal {U}_{i}$
. Since
![]() $\mathcal {U}_{i}$
is smooth, by Lemma 4.13 we may assume that
$\mathcal {U}_{i}$
is smooth, by Lemma 4.13 we may assume that
![]() $f^{\prime }_{i}(z)$
is a normalized eigenform for any
$f^{\prime }_{i}(z)$
is a normalized eigenform for any
![]() $z\in \mathcal {U}_{i}$
. For any
$z\in \mathcal {U}_{i}$
. For any
![]() $z\in \mathcal {U}_{i}\cap \mathcal {U}_{j}$
and any
$z\in \mathcal {U}_{i}\cap \mathcal {U}_{j}$
and any
![]() $h\in \mathbf {T}$
, the h-eigenvalues of
$h\in \mathbf {T}$
, the h-eigenvalues of
![]() $f^{\prime }_{i}(z)$
and
$f^{\prime }_{i}(z)$
and
![]() $f^{\prime }_{j}(z)$
are both
$f^{\prime }_{j}(z)$
are both
![]() $\varphi ^{*}(h)(z)$
. Since they are normalized eigenforms, Corollary 4.12(3) implies that the images of
$\varphi ^{*}(h)(z)$
. Since they are normalized eigenforms, Corollary 4.12(3) implies that the images of
![]() $f^{\prime }_{i}(z)$
and
$f^{\prime }_{i}(z)$
and
![]() $f^{\prime }_{j}(z)$
in
$f^{\prime }_{j}(z)$
in
 $S^{G}\left (\mu _{N},\left (\nu ^{\mathcal {U}_{i}}(z),w^{\mathcal {U}_{i}}(z)\right )\right ) (0)$
agree with each other. By Lemmas 3.1 and 3.4, we obtain
$S^{G}\left (\mu _{N},\left (\nu ^{\mathcal {U}_{i}}(z),w^{\mathcal {U}_{i}}(z)\right )\right ) (0)$
agree with each other. By Lemmas 3.1 and 3.4, we obtain
![]() $f^{\prime }_{i}(z)=f^{\prime }_{j}(z)$
.
$f^{\prime }_{i}(z)=f^{\prime }_{j}(z)$
.
Since the rigid analytic variety
 $\mathcal {IW}^{+}_{w,\mathfrak {c}}(v_{\mathrm {tot}})_{\mathbb {C}_{p}}\times \mathcal {Z}$
is reduced, this equality means that
$\mathcal {IW}^{+}_{w,\mathfrak {c}}(v_{\mathrm {tot}})_{\mathbb {C}_{p}}\times \mathcal {Z}$
is reduced, this equality means that
![]() $f^{\prime }_{i}$
and
$f^{\prime }_{i}$
and
![]() $f^{\prime }_{j}$
coincide with each other as rigid analytic functions on
$f^{\prime }_{j}$
coincide with each other as rigid analytic functions on
 $$ \begin{align*} \coprod_{\mathfrak{c}\in \left[\mathrm{Cl}^{+}(F)\right]^{\left(p\right)}} \mathcal{IW}^{+}_{w,\mathfrak{c}}(v_{\mathrm{tot}})_{\mathbb{C}_{p}} \times \left(\mathcal{U}_{i}\cap\mathcal{U}_{j}\right). \end{align*} $$
$$ \begin{align*} \coprod_{\mathfrak{c}\in \left[\mathrm{Cl}^{+}(F)\right]^{\left(p\right)}} \mathcal{IW}^{+}_{w,\mathfrak{c}}(v_{\mathrm{tot}})_{\mathbb{C}_{p}} \times \left(\mathcal{U}_{i}\cap\mathcal{U}_{j}\right). \end{align*} $$
Thus we can glue
![]() $f^{\prime }_{i}$
s to produce an element
$f^{\prime }_{i}$
s to produce an element
 $$ \begin{align*} f\in \bigoplus_{\mathfrak{c}\in \left[\mathrm{Cl}^{+}(F)\right]^{\left(p\right)}}\mathcal{O}\left(\mathcal{IW}^{+}_{w,\mathfrak{c}}(v_{\mathrm{tot}})_{\mathbb{C}_{p}}\times \mathcal{Z}\right). \end{align*} $$
$$ \begin{align*} f\in \bigoplus_{\mathfrak{c}\in \left[\mathrm{Cl}^{+}(F)\right]^{\left(p\right)}}\mathcal{O}\left(\mathcal{IW}^{+}_{w,\mathfrak{c}}(v_{\mathrm{tot}})_{\mathbb{C}_{p}}\times \mathcal{Z}\right). \end{align*} $$
This concludes the proof.
4.5.2 Gluing around cusps
Consider the unit disc
![]() $\mathcal {D}_{\mathbb {C}_{p}}$
over
$\mathcal {D}_{\mathbb {C}_{p}}$
over
![]() $\mathrm {Sp}\left (\mathbb {C}_{p}\right )$
centered at the origin O. Put
$\mathrm {Sp}\left (\mathbb {C}_{p}\right )$
centered at the origin O. Put
 $\mathcal {D}^{\times }_{\mathbb {C}_{p}}=\mathcal {D}_{\mathbb {C}_{p}}\setminus \{O\}$
.
$\mathcal {D}^{\times }_{\mathbb {C}_{p}}=\mathcal {D}_{\mathbb {C}_{p}}\setminus \{O\}$
.
Lemma 4.16. Let
![]() $\mathcal {Z}$
be a quasi-compact reduced rigid analytic variety over
$\mathcal {Z}$
be a quasi-compact reduced rigid analytic variety over
![]() $\mathbb {C}_{p}$
. Then the ring
$\mathbb {C}_{p}$
. Then the ring
 $\mathcal {O}\left (\mathcal {Z}\times \mathcal {D}^{\times }_{\mathbb {C}_{p}}\right )$
can be identified with the ring
$\mathcal {O}\left (\mathcal {Z}\times \mathcal {D}^{\times }_{\mathbb {C}_{p}}\right )$
can be identified with the ring
![]() $R_{\mathcal {Z}}$
of power series
$R_{\mathcal {Z}}$
of power series
![]() $\sum _{n\in \mathbb {Z}}a_{n} T^{n}$
with
$\sum _{n\in \mathbb {Z}}a_{n} T^{n}$
with
![]() $a_{n}\in \mathcal {O}(\mathcal {Z})$
such that
$a_{n}\in \mathcal {O}(\mathcal {Z})$
such that
 $$ \begin{align} \lim_{n\to +\infty} \sup_{z\in \mathcal{Z}} \lvert a_{n}(z)\rvert=0,\qquad \lim_{n\to +\infty} \sup_{z\in \mathcal{Z}} \lvert a_{-n}(z)\rvert\rho^{-n}=0 \end{align} $$
$$ \begin{align} \lim_{n\to +\infty} \sup_{z\in \mathcal{Z}} \lvert a_{n}(z)\rvert=0,\qquad \lim_{n\to +\infty} \sup_{z\in \mathcal{Z}} \lvert a_{-n}(z)\rvert\rho^{-n}=0 \end{align} $$
for any rational number
![]() $\rho $
satisfying
$\rho $
satisfying
![]() $0<\rho \leq 1$
.
$0<\rho \leq 1$
.
Proof. For any nonnegative rational number
![]() $\rho \leq 1$
, let
$\rho \leq 1$
, let
![]() $\mathcal {A}[\rho ,1]_{\mathbb {C}_{p}}$
be the closed annulus with parameter T over
$\mathcal {A}[\rho ,1]_{\mathbb {C}_{p}}$
be the closed annulus with parameter T over
![]() $\mathbb {C}_{p}$
defined by
$\mathbb {C}_{p}$
defined by
![]() $\rho \leq \lvert T\rvert \leq 1$
. Then we have an admissible covering
$\rho \leq \lvert T\rvert \leq 1$
. Then we have an admissible covering
 $$ \begin{align*} \mathcal{D}^{\times}_{\mathbb{C}_{p}}=\bigcup_{\rho\to 0+} \mathcal{A}[\rho,1]_{\mathbb{C}_{p}} \end{align*} $$
$$ \begin{align*} \mathcal{D}^{\times}_{\mathbb{C}_{p}}=\bigcup_{\rho\to 0+} \mathcal{A}[\rho,1]_{\mathbb{C}_{p}} \end{align*} $$
of
 $\mathcal {D}^{\times }_{\mathbb {C}_{p}}$
.
$\mathcal {D}^{\times }_{\mathbb {C}_{p}}$
.
First suppose that
![]() $\mathcal {Z}=\mathrm {Sp}(A)$
is affinoid. Let
$\mathcal {Z}=\mathrm {Sp}(A)$
is affinoid. Let
![]() $\rho $
be a rational number satisfying
$\rho $
be a rational number satisfying
![]() $0<\rho \leq 1$
. We denote by
$0<\rho \leq 1$
. We denote by
![]() $\lvert -\rvert _{\sup }$
the supremum norm on A. Since A is reduced, [Reference Bosch, Güntzer and Remmert10, Theorem 6.2.4/1] shows that
$\lvert -\rvert _{\sup }$
the supremum norm on A. Since A is reduced, [Reference Bosch, Güntzer and Remmert10, Theorem 6.2.4/1] shows that
![]() $\lvert -\rvert _{\sup }$
defines the Banach topology on A. Then the ring
$\lvert -\rvert _{\sup }$
defines the Banach topology on A. Then the ring
 $\mathcal {O}\left (\mathrm {Sp}(A)\times \mathcal {A}[\rho ,1]_{\mathbb {C}_{p}}\right )$
can be identified with the ring of power series
$\mathcal {O}\left (\mathrm {Sp}(A)\times \mathcal {A}[\rho ,1]_{\mathbb {C}_{p}}\right )$
can be identified with the ring of power series
![]() $\sum _{n\in \mathbb {Z}}a_{n} T^{n}$
with
$\sum _{n\in \mathbb {Z}}a_{n} T^{n}$
with
![]() $a_{n}\in A$
such that
$a_{n}\in A$
such that
 $$ \begin{align} \lim_{n\to +\infty} \lvert a_{n}\rvert_{\sup}=0,\qquad \lim_{n\to +\infty} \lvert a_{-n}\rvert_{\sup}\rho^{-n}=0. \end{align} $$
$$ \begin{align} \lim_{n\to +\infty} \lvert a_{n}\rvert_{\sup}=0,\qquad \lim_{n\to +\infty} \lvert a_{-n}\rvert_{\sup}\rho^{-n}=0. \end{align} $$
This identification is compatible with the restriction to
![]() $\mathcal {A}[\rho ^{\prime },1]_{\mathbb {C}_{p}}$
for any
$\mathcal {A}[\rho ^{\prime },1]_{\mathbb {C}_{p}}$
for any
![]() $\rho <\rho ^{\prime }$
, and also with the restriction to any affinoid subdomain of
$\rho <\rho ^{\prime }$
, and also with the restriction to any affinoid subdomain of
![]() $\mathrm {Sp}(A)$
. In particular, the natural map
$\mathrm {Sp}(A)$
. In particular, the natural map
 $$ \begin{align*} \mathcal{O}\left(\mathrm{Sp}(A)\times\mathcal{A}[\rho,1]_{\mathbb{C}_{p}}\right)\to \mathcal{O}\left(\mathrm{Sp}(A)\times\mathcal{A}[\rho^{\prime},1]_{\mathbb{C}_{p}}\right) \end{align*} $$
$$ \begin{align*} \mathcal{O}\left(\mathrm{Sp}(A)\times\mathcal{A}[\rho,1]_{\mathbb{C}_{p}}\right)\to \mathcal{O}\left(\mathrm{Sp}(A)\times\mathcal{A}[\rho^{\prime},1]_{\mathbb{C}_{p}}\right) \end{align*} $$
is injective for any
![]() $\rho <\rho ^{\prime }$
and thus
$\rho <\rho ^{\prime }$
and thus
 $$ \begin{align*} \mathcal{O}\left(\mathrm{Sp}(A)\times\mathcal{D}^{\times}_{\mathbb{C}_{p}}\right)=\bigcap_{\rho\to 0+} \mathcal{O}\left(\mathrm{Sp}(A)\times\mathcal{A}[\rho,1]_{\mathbb{C}_{p}}\right). \end{align*} $$
$$ \begin{align*} \mathcal{O}\left(\mathrm{Sp}(A)\times\mathcal{D}^{\times}_{\mathbb{C}_{p}}\right)=\bigcap_{\rho\to 0+} \mathcal{O}\left(\mathrm{Sp}(A)\times\mathcal{A}[\rho,1]_{\mathbb{C}_{p}}\right). \end{align*} $$
This yields an isomorphism
 $\Phi _{\mathcal {Z}}:\mathcal {O}\left (\mathcal {Z}\times \mathcal {D}^{\times }_{\mathbb {C}_{p}}\right )\simeq R_{\mathcal {Z}}$
when
$\Phi _{\mathcal {Z}}:\mathcal {O}\left (\mathcal {Z}\times \mathcal {D}^{\times }_{\mathbb {C}_{p}}\right )\simeq R_{\mathcal {Z}}$
when
![]() $\mathcal {Z}$
is affinoid, which is compatible with the restriction to any affinoid subdomain of
$\mathcal {Z}$
is affinoid, which is compatible with the restriction to any affinoid subdomain of
![]() $\mathcal {Z}$
.
$\mathcal {Z}$
.
For
![]() $\mathcal {Z}$
not necessarily affinoid, take a finite admissible affinoid covering
$\mathcal {Z}$
not necessarily affinoid, take a finite admissible affinoid covering
![]() $\mathcal {Z}=\bigcup _{i\in I} \mathcal {U}_{i}$
with
$\mathcal {Z}=\bigcup _{i\in I} \mathcal {U}_{i}$
with
![]() $\mathcal {U}_{i}=\mathrm {Sp}(A_{i})$
. Take
$\mathcal {U}_{i}=\mathrm {Sp}(A_{i})$
. Take
 $f\in \mathcal {O}\left (\mathcal {Z}\times \mathcal {D}^{\times }_{\mathbb {C}_{p}}\right )$
and write
$f\in \mathcal {O}\left (\mathcal {Z}\times \mathcal {D}^{\times }_{\mathbb {C}_{p}}\right )$
and write
 $$ \begin{align*} \Phi_{\mathcal{U}_{i}}\left(f\rvert_{\mathcal{U}_{i}\times \mathcal{D}^{\times}_{\mathbb{C}_{p}}}\right)=\sum_{n\in \mathbb{Z}} a_{i,n} T^{n} \end{align*} $$
$$ \begin{align*} \Phi_{\mathcal{U}_{i}}\left(f\rvert_{\mathcal{U}_{i}\times \mathcal{D}^{\times}_{\mathbb{C}_{p}}}\right)=\sum_{n\in \mathbb{Z}} a_{i,n} T^{n} \end{align*} $$
with
![]() $a_{i,n}\in A_{i}$
. Then
$a_{i,n}\in A_{i}$
. Then
![]() $a_{i,n}$
s can be glued to obtain an element
$a_{i,n}$
s can be glued to obtain an element
![]() $a_{n}\in \mathcal {O}(\mathcal {Z})$
. Put
$a_{n}\in \mathcal {O}(\mathcal {Z})$
. Put
![]() $\Phi (f)=\sum _{n\in \mathbb {Z}} a_{n} T^{n}$
. Since I is a finite set, we can check that
$\Phi (f)=\sum _{n\in \mathbb {Z}} a_{n} T^{n}$
. Since I is a finite set, we can check that
![]() $a_{n}$
s also satisfy equation (4.14) and thus
$a_{n}$
s also satisfy equation (4.14) and thus
![]() $\Phi (f)\in R_{\mathcal {Z}}$
. On the other hand, for any element
$\Phi (f)\in R_{\mathcal {Z}}$
. On the other hand, for any element
![]() $g=\sum _{n\in \mathbb {Z}} a_{n} T^{n}$
of
$g=\sum _{n\in \mathbb {Z}} a_{n} T^{n}$
of
![]() $R_{\mathcal {Z}}$
, put
$R_{\mathcal {Z}}$
, put
![]() $\Psi (g)_{i}=\sum _{n\in \mathbb {Z}} a_{n}\rvert _{\mathcal {U}_{i}} T^{n}$
. Then
$\Psi (g)_{i}=\sum _{n\in \mathbb {Z}} a_{n}\rvert _{\mathcal {U}_{i}} T^{n}$
. Then
![]() $\Psi (g)_{i}\in R_{\mathcal {U}_{i}}$
and the elements
$\Psi (g)_{i}\in R_{\mathcal {U}_{i}}$
and the elements
 $\Phi _{\mathcal {U}_{i}}^{-1}(\Psi (g)_{i})\in \mathcal {O}\left (\mathcal {U}_{i}\times \mathcal {D}^{\times }_{\mathbb {C}_{p}}\right )$
can be glued to obtain an element
$\Phi _{\mathcal {U}_{i}}^{-1}(\Psi (g)_{i})\in \mathcal {O}\left (\mathcal {U}_{i}\times \mathcal {D}^{\times }_{\mathbb {C}_{p}}\right )$
can be glued to obtain an element
 $\Psi (g)\in \mathcal {O}\left (\mathcal {Z}\times \mathcal {D}^{\times }_{\mathbb {C}_{p}}\right )$
. Then
$\Psi (g)\in \mathcal {O}\left (\mathcal {Z}\times \mathcal {D}^{\times }_{\mathbb {C}_{p}}\right )$
. Then
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
are inverse to each other and the lemma follows.
$\Psi $
are inverse to each other and the lemma follows.
Next we show the following variant of [Reference Buzzard and Calegari13, Lemma 7.1]:
Lemma 4.17. Let
![]() $\mathcal {Z}$
be a quasi-compact smooth rigid analytic variety over
$\mathcal {Z}$
be a quasi-compact smooth rigid analytic variety over
![]() $\mathbb {C}_{p}$
. Let
$\mathbb {C}_{p}$
. Let
![]() $\mathcal {V}$
be an admissible open subset of
$\mathcal {V}$
be an admissible open subset of
![]() $\mathcal {Z}$
which meets every connected component of
$\mathcal {Z}$
which meets every connected component of
![]() $\mathcal {Z}$
. Let f be an element of
$\mathcal {Z}$
. Let f be an element of
 $\mathcal {O}\left (\mathcal {Z}\times \mathcal {D}^{\times }_{\mathbb {C}_{p}}\right )$
. Suppose that
$\mathcal {O}\left (\mathcal {Z}\times \mathcal {D}^{\times }_{\mathbb {C}_{p}}\right )$
. Suppose that
 $f\rvert _{\mathcal {V}\times \mathcal {D}^{\times }_{\mathbb {C}_{p}}}$
extends to an element of
$f\rvert _{\mathcal {V}\times \mathcal {D}^{\times }_{\mathbb {C}_{p}}}$
extends to an element of
 $\mathcal {O}\left (\mathcal {V} \times \mathcal {D}_{\mathbb {C}_{p}}\right )$
. Then f extends to an element of
$\mathcal {O}\left (\mathcal {V} \times \mathcal {D}_{\mathbb {C}_{p}}\right )$
. Then f extends to an element of
 $\mathcal {O}\left (\mathcal {Z}\times \mathcal {D}_{\mathbb {C}_{p}}\right )$
.
$\mathcal {O}\left (\mathcal {Z}\times \mathcal {D}_{\mathbb {C}_{p}}\right )$
.
Proof. By taking an admissible affinoid open subset of the intersection of
![]() $\mathcal {V}$
and each connected component of
$\mathcal {V}$
and each connected component of
![]() $\mathcal {Z}$
and replacing
$\mathcal {Z}$
and replacing
![]() $\mathcal {V}$
with their union, we may assume that
$\mathcal {V}$
with their union, we may assume that
![]() $\mathcal {V}$
is quasi-compact. By Lemma 3.1, the assumption on
$\mathcal {V}$
is quasi-compact. By Lemma 3.1, the assumption on
![]() $\mathcal {V}$
yields injections
$\mathcal {V}$
yields injections
 $$ \begin{align*} \mathcal{O}(\mathcal{Z})\to \mathcal{O}(\mathcal{V}),\qquad \mathcal{O}\left(\mathcal{Z}\times\mathcal{D}^{\times}_{\mathbb{C}_{p}}\right) \to \mathcal{O}\left(\mathcal{V}\times \mathcal{D}^{\times}_{\mathbb{C}_{p}}\right) \gets \mathcal{O}\left(\mathcal{V}\times \mathcal{D}_{\mathbb{C}_{p}}\right). \end{align*} $$
$$ \begin{align*} \mathcal{O}(\mathcal{Z})\to \mathcal{O}(\mathcal{V}),\qquad \mathcal{O}\left(\mathcal{Z}\times\mathcal{D}^{\times}_{\mathbb{C}_{p}}\right) \to \mathcal{O}\left(\mathcal{V}\times \mathcal{D}^{\times}_{\mathbb{C}_{p}}\right) \gets \mathcal{O}\left(\mathcal{V}\times \mathcal{D}_{\mathbb{C}_{p}}\right). \end{align*} $$
From Lemma 4.16, we see that the intersection of
 $\mathcal {O}\left (\mathcal {Z}\times \mathcal {D}^{\times }_{\mathbb {C}_{p}}\right )$
and
$\mathcal {O}\left (\mathcal {Z}\times \mathcal {D}^{\times }_{\mathbb {C}_{p}}\right )$
and
 $\mathcal {O}\left (\mathcal {V}\times \mathcal {D}_{\mathbb {C}_{p}}\right )$
inside
$\mathcal {O}\left (\mathcal {V}\times \mathcal {D}_{\mathbb {C}_{p}}\right )$
inside
 $\mathcal {O}\left (\mathcal {V}\times \mathcal {D}^{\times }_{\mathbb {C}_{p}}\right )$
is the set of formal power series
$\mathcal {O}\left (\mathcal {V}\times \mathcal {D}^{\times }_{\mathbb {C}_{p}}\right )$
is the set of formal power series
 $\sum _{n\geq 0} a_{n} T^{n}$
with
$\sum _{n\geq 0} a_{n} T^{n}$
with
![]() $a_{n}\in \mathcal {O}(\mathcal {Z})$
satisfying
$a_{n}\in \mathcal {O}(\mathcal {Z})$
satisfying
 $$ \begin{align*} \lim_{n\to +\infty} \sup_{z\in \mathcal{Z}} \lvert a_{n}(z)\rvert=0, \end{align*} $$
$$ \begin{align*} \lim_{n\to +\infty} \sup_{z\in \mathcal{Z}} \lvert a_{n}(z)\rvert=0, \end{align*} $$
which is equal to
 $\mathcal {O}\left (\mathcal {Z}\times \mathcal {D}_{\mathbb {C}_{p}}\right )$
.
$\mathcal {O}\left (\mathcal {Z}\times \mathcal {D}_{\mathbb {C}_{p}}\right )$
.
Lemma 4.18.
 $$ \begin{align*} \mathcal{O}^{\circ}\left(\mathcal{D}^{\times}_{\mathbb{C}_{p}}\right)\subseteq \mathcal{O}\left(\mathcal{D}_{\mathbb{C}_{p}}\right). \end{align*} $$
$$ \begin{align*} \mathcal{O}^{\circ}\left(\mathcal{D}^{\times}_{\mathbb{C}_{p}}\right)\subseteq \mathcal{O}\left(\mathcal{D}_{\mathbb{C}_{p}}\right). \end{align*} $$
Proof. Let
![]() $f=\sum _{n\in \mathbb {Z}} a_{n} T^{n}$
be an element of
$f=\sum _{n\in \mathbb {Z}} a_{n} T^{n}$
be an element of
 $\mathcal {O}^{\circ }\left (\mathcal {D}^{\times }_{\mathbb {C}_{p}}\right )$
. Consider the Newton polygon of f. Then the assumption implies that any point
$\mathcal {O}^{\circ }\left (\mathcal {D}^{\times }_{\mathbb {C}_{p}}\right )$
. Consider the Newton polygon of f. Then the assumption implies that any point
![]() $\left (n,v_{p}(a_{n})\right )$
lies above the line
$\left (n,v_{p}(a_{n})\right )$
lies above the line
![]() $y=-rx$
for any nonnegative rational number r, which forces
$y=-rx$
for any nonnegative rational number r, which forces
![]() $a_{n}=0$
for any
$a_{n}=0$
for any
![]() $n<0$
.
$n<0$
.
Proposition 4.19. Let
 $\varphi :\mathcal {D}^{\times }_{\mathbb {C}_{p}}\to (\mathcal {E}\rvert _{\mathcal {X}})_{\mathbb {C}_{p}}$
be a morphism of rigid analytic varieties over
$\varphi :\mathcal {D}^{\times }_{\mathbb {C}_{p}}\to (\mathcal {E}\rvert _{\mathcal {X}})_{\mathbb {C}_{p}}$
be a morphism of rigid analytic varieties over
![]() $\mathbb {C}_{p}$
such that the composite
$\mathbb {C}_{p}$
such that the composite
 $\mathcal {D}^{\times }_{\mathbb {C}_{p}} \to (\mathcal {E}\rvert {}_{\mathcal {X}})_{\mathbb {C}_{p}}\to \mathcal {X}_{\mathbb {C}_{p}}$
extends to an n-analytic map
$\mathcal {D}^{\times }_{\mathbb {C}_{p}} \to (\mathcal {E}\rvert {}_{\mathcal {X}})_{\mathbb {C}_{p}}\to \mathcal {X}_{\mathbb {C}_{p}}$
extends to an n-analytic map
![]() $\mathcal {D}_{\mathbb {C}_{p}}\to \mathcal {X}_{\mathbb {C}_{p}}$
. Let
$\mathcal {D}_{\mathbb {C}_{p}}\to \mathcal {X}_{\mathbb {C}_{p}}$
. Let
 $\left (\nu ^{\mathcal {D}_{\mathbb {C}_{p}}},w^{\mathcal {D}_{\mathbb {C}_{p}}}\right )$
be the weight associated to the map
$\left (\nu ^{\mathcal {D}_{\mathbb {C}_{p}}},w^{\mathcal {D}_{\mathbb {C}_{p}}}\right )$
be the weight associated to the map
![]() $\mathcal {D}_{\mathbb {C}_{p}}\to \mathcal {X}_{\mathbb {C}_{p}}$
. Suppose that for some nonnegative rational number
$\mathcal {D}_{\mathbb {C}_{p}}\to \mathcal {X}_{\mathbb {C}_{p}}$
. Suppose that for some nonnegative rational number
![]() $v^{\prime }<(p-1)/p^{n}$
, we are given an element
$v^{\prime }<(p-1)/p^{n}$
, we are given an element
 $$ \begin{align*} f=(f_{\mathfrak{c}})_{\mathfrak{c}\in\left[\mathrm{Cl}^{+}(F)\right]^{\left(p\right)}}\in \bigoplus_{\mathfrak{c}\in \left[\mathrm{Cl}^{+}(F)\right]^{\left(p\right)}} \mathcal{O}\left(\mathcal{IW}_{w,\mathfrak{c}}^{+}(v^{\prime})_{\mathbb{C}_{p}}\times \mathcal{D}^{\times}_{\mathbb{C}_{p}}\right) \end{align*} $$
$$ \begin{align*} f=(f_{\mathfrak{c}})_{\mathfrak{c}\in\left[\mathrm{Cl}^{+}(F)\right]^{\left(p\right)}}\in \bigoplus_{\mathfrak{c}\in \left[\mathrm{Cl}^{+}(F)\right]^{\left(p\right)}} \mathcal{O}\left(\mathcal{IW}_{w,\mathfrak{c}}^{+}(v^{\prime})_{\mathbb{C}_{p}}\times \mathcal{D}^{\times}_{\mathbb{C}_{p}}\right) \end{align*} $$
and an admissible affinoid covering
 $\mathcal {D}^{\times }_{\mathbb {C}_{p}}=\bigcup _{i\in I} \mathcal {U}_{i}$
such that the restriction
$\mathcal {D}^{\times }_{\mathbb {C}_{p}}=\bigcup _{i\in I} \mathcal {U}_{i}$
such that the restriction
![]() $f\rvert _{\mathcal {U}_{i}}$
for each
$f\rvert _{\mathcal {U}_{i}}$
for each
![]() $i\in I$
is an eigenform of
$i\in I$
is an eigenform of
 $S^{G}\left (\mu _{N}, \left (\nu ^{\mathcal {U}_{i}},w^{\mathcal {U}_{i}}\right )\right )(v^{\prime })$
with eigensystem
$S^{G}\left (\mu _{N}, \left (\nu ^{\mathcal {U}_{i}},w^{\mathcal {U}_{i}}\right )\right )(v^{\prime })$
with eigensystem
 $\varphi ^{*}: \mathbf {T}\to \mathcal {O}\left (\mathcal {D}_{\mathbb {C}_{p}}^{\times }\right )\to \mathcal {O}(\mathcal {U}_{i})$
and
$\varphi ^{*}: \mathbf {T}\to \mathcal {O}\left (\mathcal {D}_{\mathbb {C}_{p}}^{\times }\right )\to \mathcal {O}(\mathcal {U}_{i})$
and
![]() $f(z)$
is normalized for any
$f(z)$
is normalized for any
 $z\in \mathcal {D}^{\times }_{\mathbb {C}_{p}}$
. Then there exists an eigenform
$z\in \mathcal {D}^{\times }_{\mathbb {C}_{p}}$
. Then there exists an eigenform
 $f^{\prime }\in S^{G}\left (\mu _{N},\left (\nu ^{\mathcal {D}_{\mathbb {C}_{p}}},w^{\mathcal {D}_{\mathbb {C}_{p}}}\right )\right )(v^{\prime })$
such that
$f^{\prime }\in S^{G}\left (\mu _{N},\left (\nu ^{\mathcal {D}_{\mathbb {C}_{p}}},w^{\mathcal {D}_{\mathbb {C}_{p}}}\right )\right )(v^{\prime })$
such that
![]() $f^{\prime }(z)$
is normalized for any
$f^{\prime }(z)$
is normalized for any
![]() $z\in \mathcal {D}_{\mathbb {C}_{p}}$
, and it is an eigenform with eigensystem
$z\in \mathcal {D}_{\mathbb {C}_{p}}$
, and it is an eigenform with eigensystem
 $\varphi ^{*}(z): \mathbf {T}\to \mathcal {O}\left (\mathcal {D}^{\times }_{\mathbb {C}_{p}}\right )\to \mathbb {C}_{p}$
for any
$\varphi ^{*}(z): \mathbf {T}\to \mathcal {O}\left (\mathcal {D}^{\times }_{\mathbb {C}_{p}}\right )\to \mathbb {C}_{p}$
for any
 $z\in \mathcal {D}^{\times }_{\mathbb {C}_{p}}$
.
$z\in \mathcal {D}^{\times }_{\mathbb {C}_{p}}$
.
Proof. Consider the map
 $\pi _{w}^{\mathrm {rig}}: \mathcal {IW}_{w,\mathfrak {c}}^{+}(v^{\prime })_{\mathbb {C}_{p}} \to \bar {\mathcal {M}}(\mu _{N},\mathfrak {c})(v^{\prime })_{\mathbb {C}_{p}}$
as before. Let
$\pi _{w}^{\mathrm {rig}}: \mathcal {IW}_{w,\mathfrak {c}}^{+}(v^{\prime })_{\mathbb {C}_{p}} \to \bar {\mathcal {M}}(\mu _{N},\mathfrak {c})(v^{\prime })_{\mathbb {C}_{p}}$
as before. Let
![]() $\mathcal {S}_{\mathfrak {c}}$
be an admissible affinoid open subset of
$\mathcal {S}_{\mathfrak {c}}$
be an admissible affinoid open subset of
![]() $\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})(v^{\prime })_{\mathbb {C}_{p}}$
as in Corollary 4.12(1). Put
$\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})(v^{\prime })_{\mathbb {C}_{p}}$
as in Corollary 4.12(1). Put
 $\mathcal {I}_{\mathfrak {c}}=\left (\pi _{w}^{\mathrm {rig}}\right )^{-1}(\mathcal {S}_{\mathfrak {c}})$
. Then
$\mathcal {I}_{\mathfrak {c}}=\left (\pi _{w}^{\mathrm {rig}}\right )^{-1}(\mathcal {S}_{\mathfrak {c}})$
. Then
![]() $\mathcal {I}_{\mathfrak {c}}$
is an admissible open subset which meets every connected component of
$\mathcal {I}_{\mathfrak {c}}$
is an admissible open subset which meets every connected component of
 $\mathcal {IW}_{w,\mathfrak {c}}^{+}(v^{\prime })_{\mathbb {C}_{p}}$
such that
$\mathcal {IW}_{w,\mathfrak {c}}^{+}(v^{\prime })_{\mathbb {C}_{p}}$
such that
![]() $f_{\mathfrak {c}}(z)\rvert _{\mathcal {I}_{\mathfrak {c}}}$
has absolute value bounded by
$f_{\mathfrak {c}}(z)\rvert _{\mathcal {I}_{\mathfrak {c}}}$
has absolute value bounded by
![]() $1$
for any
$1$
for any
 $z\in \mathcal {D}^{\times }_{\mathbb {C}_{p}}$
. Hence
$z\in \mathcal {D}^{\times }_{\mathbb {C}_{p}}$
. Hence
 $f_{\mathfrak {c}}\rvert _{\mathcal {I}_{\mathfrak {c}}\times \mathcal {D}^{\times }_{\mathbb {C}_{p}}}$
also has absolute value bounded by
$f_{\mathfrak {c}}\rvert _{\mathcal {I}_{\mathfrak {c}}\times \mathcal {D}^{\times }_{\mathbb {C}_{p}}}$
also has absolute value bounded by
![]() $1$
.
$1$
.
Note that
![]() $\mathcal {I}_{\mathfrak {c}}$
is quasi-compact, since
$\mathcal {I}_{\mathfrak {c}}$
is quasi-compact, since
![]() $\pi _{w}$
is quasi-compact. By Lemma 4.16, we can write
$\pi _{w}$
is quasi-compact. By Lemma 4.16, we can write
 $$ \begin{align*} f_{\mathfrak{c}}\rvert_{\mathcal{I}_{\mathfrak{c}}\times \mathcal{D}^{\times}_{\mathbb{C}_{p}}}=\sum_{n\in \mathbb{Z}} a_{n} T^{n} \end{align*} $$
$$ \begin{align*} f_{\mathfrak{c}}\rvert_{\mathcal{I}_{\mathfrak{c}}\times \mathcal{D}^{\times}_{\mathbb{C}_{p}}}=\sum_{n\in \mathbb{Z}} a_{n} T^{n} \end{align*} $$
with some
![]() $a_{n}\in \mathcal {O}(\mathcal {I}_{\mathfrak {c}})$
. Lemma 4.18 implies
$a_{n}\in \mathcal {O}(\mathcal {I}_{\mathfrak {c}})$
. Lemma 4.18 implies
![]() $a_{n}(x)=0$
for any
$a_{n}(x)=0$
for any
![]() $x\in \mathcal {I}_{\mathfrak {c}}$
and any
$x\in \mathcal {I}_{\mathfrak {c}}$
and any
![]() $n<0$
. Since
$n<0$
. Since
![]() $\mathcal {I}_{\mathfrak {c}}$
is reduced, we obtain
$\mathcal {I}_{\mathfrak {c}}$
is reduced, we obtain
![]() $a_{n}=0$
for any
$a_{n}=0$
for any
![]() $n<0$
and thus
$n<0$
and thus
 $$ \begin{align*} f_{\mathfrak{c}}\rvert_{\mathcal{I}_{\mathfrak{c}}\times \mathcal{D}^{\times}_{\mathbb{C}_{p}}}\in \mathcal{O}\left(\mathcal{I}_{\mathfrak{c}}\times \mathcal{D}_{\mathbb{C}_{p}}\right). \end{align*} $$
$$ \begin{align*} f_{\mathfrak{c}}\rvert_{\mathcal{I}_{\mathfrak{c}}\times \mathcal{D}^{\times}_{\mathbb{C}_{p}}}\in \mathcal{O}\left(\mathcal{I}_{\mathfrak{c}}\times \mathcal{D}_{\mathbb{C}_{p}}\right). \end{align*} $$
Therefore, by Lemma 4.17 we see that
![]() $f_{\mathfrak {c}}$
extends to an element
$f_{\mathfrak {c}}$
extends to an element
![]() $\tilde {f}_{\mathfrak {c}}$
of
$\tilde {f}_{\mathfrak {c}}$
of
 $\mathcal {O}\left (\mathcal {IW}_{w,\mathfrak {c}}^{+}(v^{\prime })_{\mathbb {C}_{p}}\times\mathcal {D}_{\mathbb {C}_{p}}\right )$
.
$\mathcal {O}\left (\mathcal {IW}_{w,\mathfrak {c}}^{+}(v^{\prime })_{\mathbb {C}_{p}}\times\mathcal {D}_{\mathbb {C}_{p}}\right )$
.
Write
![]() $\mathcal {D}_{\mathbb {C}_{p}}=\mathrm {Sp}\left (\mathbb {C}_{p}\langle T\rangle \right )$
. Note that the ring
$\mathcal {D}_{\mathbb {C}_{p}}=\mathrm {Sp}\left (\mathbb {C}_{p}\langle T\rangle \right )$
. Note that the ring
 $\mathcal {O}\left (\mathcal {IW}_{w,\mathfrak {c}}^{+}(v^{\prime })_{\mathbb {C}_{p}}\times \mathcal {D}_{\mathbb {C}_{p}}\right )$
is T-torsion free. We claim that if
$\mathcal {O}\left (\mathcal {IW}_{w,\mathfrak {c}}^{+}(v^{\prime })_{\mathbb {C}_{p}}\times \mathcal {D}_{\mathbb {C}_{p}}\right )$
is T-torsion free. We claim that if
![]() $f_{\mathfrak {c}}\neq 0$
, then there exists a nonnegative integer
$f_{\mathfrak {c}}\neq 0$
, then there exists a nonnegative integer
![]() $m_{\mathfrak {c}}$
satisfying
$m_{\mathfrak {c}}$
satisfying
 $$ \begin{align*} \tilde{f}_{\mathfrak{c}}\in T^{m_{\mathfrak{c}}} \mathcal{O}\left(\mathcal{IW}_{w,\mathfrak{c}}^{+}(v^{\prime})_{\mathbb{C}_{p}}\times \mathcal{D}_{\mathbb{C}_{p}}\right)\setminus T^{m_{\mathfrak{c}}+1} \mathcal{O}\left(\mathcal{IW}_{w,\mathfrak{c}}^{+}(v^{\prime})_{\mathbb{C}_{p}}\times \mathcal{D}_{\mathbb{C}_{p}}\right). \end{align*} $$
$$ \begin{align*} \tilde{f}_{\mathfrak{c}}\in T^{m_{\mathfrak{c}}} \mathcal{O}\left(\mathcal{IW}_{w,\mathfrak{c}}^{+}(v^{\prime})_{\mathbb{C}_{p}}\times \mathcal{D}_{\mathbb{C}_{p}}\right)\setminus T^{m_{\mathfrak{c}}+1} \mathcal{O}\left(\mathcal{IW}_{w,\mathfrak{c}}^{+}(v^{\prime})_{\mathbb{C}_{p}}\times \mathcal{D}_{\mathbb{C}_{p}}\right). \end{align*} $$
Indeed, since
 $\mathcal {IW}_{w,\mathfrak {c}}^{+}(v^{\prime })_{\mathbb {C}_{p}}$
is smooth, we can take an admissible affinoid covering
$\mathcal {IW}_{w,\mathfrak {c}}^{+}(v^{\prime })_{\mathbb {C}_{p}}$
is smooth, we can take an admissible affinoid covering
 $$ \begin{align*} \mathcal{IW}_{w,\mathfrak{c}}^{+}(v^{\prime})_{\mathbb{C}_{p}}=\bigcup_{j\in J}\mathcal{V}_{j},\quad \mathcal{V}_{j}=\mathrm{Sp}\left(A_{j}\right), \end{align*} $$
$$ \begin{align*} \mathcal{IW}_{w,\mathfrak{c}}^{+}(v^{\prime})_{\mathbb{C}_{p}}=\bigcup_{j\in J}\mathcal{V}_{j},\quad \mathcal{V}_{j}=\mathrm{Sp}\left(A_{j}\right), \end{align*} $$
such that every
![]() $A_{j}$
is a Noetherian domain. Suppose that
$A_{j}$
is a Noetherian domain. Suppose that
 $$ \begin{align*} \tilde{f}_{\mathfrak{c}}\in \bigcap_{m\geq 0} T^{m} \mathcal{O}\left(\mathcal{IW}_{w,\mathfrak{c}}^{+}(v^{\prime})_{\mathbb{C}_{p}}\times \mathcal{D}_{\mathbb{C}_{p}}\right). \end{align*} $$
$$ \begin{align*} \tilde{f}_{\mathfrak{c}}\in \bigcap_{m\geq 0} T^{m} \mathcal{O}\left(\mathcal{IW}_{w,\mathfrak{c}}^{+}(v^{\prime})_{\mathbb{C}_{p}}\times \mathcal{D}_{\mathbb{C}_{p}}\right). \end{align*} $$
Since
![]() $A_{j}\langle T\rangle $
is also a Noetherian domain, Krull’s intersection theorem implies
$A_{j}\langle T\rangle $
is also a Noetherian domain, Krull’s intersection theorem implies
 $\tilde {f}_{\mathfrak {c}}\rvert _{\mathcal {V}_{j}\times \mathcal {D}_{\mathbb {C}_{p}}}=0$
for any
$\tilde {f}_{\mathfrak {c}}\rvert _{\mathcal {V}_{j}\times \mathcal {D}_{\mathbb {C}_{p}}}=0$
for any
![]() $j\in J$
and thus
$j\in J$
and thus
![]() $\tilde {f}_{\mathfrak {c}}=0$
, which is a contradiction.
$\tilde {f}_{\mathfrak {c}}=0$
, which is a contradiction.
Put
 $m=\min \left \{m_{\mathfrak {c}}\mid \mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{(p)},f_{\mathfrak {c}}\neq 0\right \}$
. Let
$m=\min \left \{m_{\mathfrak {c}}\mid \mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{(p)},f_{\mathfrak {c}}\neq 0\right \}$
. Let
![]() $\tilde {f}^{\prime }_{\mathfrak {c}}$
be the unique element of
$\tilde {f}^{\prime }_{\mathfrak {c}}$
be the unique element of
 $\mathcal {O}\left (\mathcal {IW}_{w,\mathfrak {c}}^{+}(v^{\prime })_{\mathbb {C}_{p}}\times \mathcal {D}_{\mathbb {C}_{p}}\right )$
satisfying
$\mathcal {O}\left (\mathcal {IW}_{w,\mathfrak {c}}^{+}(v^{\prime })_{\mathbb {C}_{p}}\times \mathcal {D}_{\mathbb {C}_{p}}\right )$
satisfying
 $\tilde {f}_{\mathfrak {c}}=T^{m} \tilde {f}^{\prime }_{\mathfrak {c}}$
. Since the maps
$\tilde {f}_{\mathfrak {c}}=T^{m} \tilde {f}^{\prime }_{\mathfrak {c}}$
. Since the maps
 $$ \begin{align*} \mathcal{O}\left(\mathcal{IW}_{w,\mathfrak{c}}^{+}(v^{\prime})_{\mathbb{C}_{p}}\times \mathcal{D}_{\mathbb{C}_{p}}\right)&\to \mathcal{O}\left(\mathcal{IW}_{w,\mathfrak{c}}^{+}(v^{\prime})_{\mathbb{C}_{p}}\times \mathcal{D}^{\times}_{\mathbb{C}_{p}}\right)\\ &\to \prod_{i\in I} \mathcal{O}\left(\mathcal{IW}_{w,\mathfrak{c}}^{+}(v^{\prime})_{\mathbb{C}_{p}}\times \mathcal{U}_{i}\right) \end{align*} $$
$$ \begin{align*} \mathcal{O}\left(\mathcal{IW}_{w,\mathfrak{c}}^{+}(v^{\prime})_{\mathbb{C}_{p}}\times \mathcal{D}_{\mathbb{C}_{p}}\right)&\to \mathcal{O}\left(\mathcal{IW}_{w,\mathfrak{c}}^{+}(v^{\prime})_{\mathbb{C}_{p}}\times \mathcal{D}^{\times}_{\mathbb{C}_{p}}\right)\\ &\to \prod_{i\in I} \mathcal{O}\left(\mathcal{IW}_{w,\mathfrak{c}}^{+}(v^{\prime})_{\mathbb{C}_{p}}\times \mathcal{U}_{i}\right) \end{align*} $$
are injective by Lemma 3.1, the element
![]() $\tilde {f}^{\prime }_{\mathfrak {c}}$
is also
$\tilde {f}^{\prime }_{\mathfrak {c}}$
is also
![]() $\kappa ^{\mathcal {D}_{\mathbb {C}_{p}}}$
-equivariant and
$\kappa ^{\mathcal {D}_{\mathbb {C}_{p}}}$
-equivariant and
![]() $\Delta $
-stable. Moreover, note that the restriction map
$\Delta $
-stable. Moreover, note that the restriction map
 $\mathcal {O}\left (\mathcal {V}\times \mathcal {D}_{\mathbb {C}_{p}}\right )\to \mathcal {O}\left (\mathcal {V}\times \mathcal {D}^{\times }_{\mathbb {C}_{p}}\right )$
is injective for any
$\mathcal {O}\left (\mathcal {V}\times \mathcal {D}_{\mathbb {C}_{p}}\right )\to \mathcal {O}\left (\mathcal {V}\times \mathcal {D}^{\times }_{\mathbb {C}_{p}}\right )$
is injective for any
![]() $\mathbb {C}_{p}$
-affinoid variety
$\mathbb {C}_{p}$
-affinoid variety
![]() $\mathcal {V}$
. For the boundary divisor D of
$\mathcal {V}$
. For the boundary divisor D of
![]() $\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})(v^{\prime })_{\mathbb {C}_{p}}$
, we have the commutative diagram
$\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})(v^{\prime })_{\mathbb {C}_{p}}$
, we have the commutative diagram

where the vertical arrows are injective and the bottom arrow is bijective. This implies that the element
![]() $\tilde {f}^{\prime }_{\mathfrak {c}}$
is a cusp form. Hence the collection
$\tilde {f}^{\prime }_{\mathfrak {c}}$
is a cusp form. Hence the collection
 $\tilde {f}^{\prime }=\left (\tilde {f}^{\prime }_{\mathfrak {c}}\right )_{\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{\left (p\right )}}$
is an element of
$\tilde {f}^{\prime }=\left (\tilde {f}^{\prime }_{\mathfrak {c}}\right )_{\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{\left (p\right )}}$
is an element of
 $S^{G}\left (\mu _{N},\left (\nu ^{\mathcal {D}_{\mathbb {C}_{p}}},w^{\mathcal {D}_{\mathbb {C}_{p}}}\right )\right )(v^{\prime })$
such that
$S^{G}\left (\mu _{N},\left (\nu ^{\mathcal {D}_{\mathbb {C}_{p}}},w^{\mathcal {D}_{\mathbb {C}_{p}}}\right )\right )(v^{\prime })$
such that
 $\tilde {f}^{\prime }(z)\neq 0$
for any
$\tilde {f}^{\prime }(z)\neq 0$
for any
![]() $z\in \mathcal {D}_{\mathbb {C}_{p}}$
.
$z\in \mathcal {D}_{\mathbb {C}_{p}}$
.
Let
![]() $\Lambda (\mathfrak {n})$
be the image of
$\Lambda (\mathfrak {n})$
be the image of
![]() $T_{\mathfrak {n}}$
(resp.,
$T_{\mathfrak {n}}$
(resp.,
![]() $S_{\mathfrak {n}}$
) by the map
$S_{\mathfrak {n}}$
) by the map
 $\varphi ^{*}: \mathbf {T}\to \mathcal {O}\left (\mathcal {D}^{\times }_{\mathbb {C}_{p}}\right )$
. By Corollary 4.10, the specialization
$\varphi ^{*}: \mathbf {T}\to \mathcal {O}\left (\mathcal {D}^{\times }_{\mathbb {C}_{p}}\right )$
. By Corollary 4.10, the specialization
![]() $\Lambda (\mathfrak {n})(z)$
is p-integral for any
$\Lambda (\mathfrak {n})(z)$
is p-integral for any
 $z\in \mathcal {D}^{\times }_{\mathbb {C}_{p}}$
. Thus Lemma 4.18 shows
$z\in \mathcal {D}^{\times }_{\mathbb {C}_{p}}$
. Thus Lemma 4.18 shows
 $\Lambda (\mathfrak {n})\in \mathcal {O}\left (\mathcal {D}_{\mathbb {C}_{p}}\right )$
. By the injectivity mentioned above, we see that
$\Lambda (\mathfrak {n})\in \mathcal {O}\left (\mathcal {D}_{\mathbb {C}_{p}}\right )$
. By the injectivity mentioned above, we see that
![]() $\tilde {f}^{\prime }$
is an eigenform on which
$\tilde {f}^{\prime }$
is an eigenform on which
![]() $T_{\mathfrak {n}}$
(resp.,
$T_{\mathfrak {n}}$
(resp.,
![]() $S_{\mathfrak {n}}$
) acts by
$S_{\mathfrak {n}}$
) acts by
![]() $\Lambda (\mathfrak {n})$
. Now Lemma 4.13 concludes the proof of the proposition.
$\Lambda (\mathfrak {n})$
. Now Lemma 4.13 concludes the proof of the proposition.
5 Properness at integral weights
Let
![]() $\mathcal {E}\to \mathcal {W}^{G}$
be the Hilbert eigenvariety as in §3.3.3. Let
$\mathcal {E}\to \mathcal {W}^{G}$
be the Hilbert eigenvariety as in §3.3.3. Let
![]() $\mathcal {D}_{\mathbb {C}_{p}}$
be the unit disc over
$\mathcal {D}_{\mathbb {C}_{p}}$
be the unit disc over
![]() $\mathrm {Sp}\left (\mathbb {C}_{p}\right )$
centered at the origin O and put
$\mathrm {Sp}\left (\mathbb {C}_{p}\right )$
centered at the origin O and put
 $\mathcal {D}^{\times }_{\mathbb {C}_{p}}=\mathcal {D}_{\mathbb {C}_{p}}\setminus \{O\}$
. In this section, we prove the following main theorem of this paper:
$\mathcal {D}^{\times }_{\mathbb {C}_{p}}=\mathcal {D}_{\mathbb {C}_{p}}\setminus \{O\}$
. In this section, we prove the following main theorem of this paper:
Theorem 5.1. Suppose that F is unramified over p and that for any prime ideal
![]() $\mathfrak {p}\mid p$
of F, the residue degree
$\mathfrak {p}\mid p$
of F, the residue degree
![]() $f_{\mathfrak {p}}$
satisfies
$f_{\mathfrak {p}}$
satisfies
![]() $f_{\mathfrak {p}}\leq 2$
(resp., p splits completely in F) for
$f_{\mathfrak {p}}\leq 2$
(resp., p splits completely in F) for
![]() $p\geq 3$
(resp.,
$p\geq 3$
(resp.,
![]() $p=2$
). Consider a commutative diagram
$p=2$
). Consider a commutative diagram

of rigid analytic varieties over
![]() $\mathbb {C}_{p}$
, where the left vertical arrow is the natural inclusion. Suppose that
$\mathbb {C}_{p}$
, where the left vertical arrow is the natural inclusion. Suppose that
![]() $\psi (O)$
is
$\psi (O)$
is
![]() $1$
-integral (resp.,
$1$
-integral (resp.,
![]() $1$
-doubly even) in the sense of §3.3.2. Then there exists a morphism
$1$
-doubly even) in the sense of §3.3.2. Then there exists a morphism
![]() $\mathcal {D}_{\mathbb {C}_{p}}\to \mathcal {E}_{\mathbb {C}_{p}}$
of rigid analytic varieties over
$\mathcal {D}_{\mathbb {C}_{p}}\to \mathcal {E}_{\mathbb {C}_{p}}$
of rigid analytic varieties over
![]() $\mathbb {C}_{p}$
such that the diagram with this morphism added is also commutative.
$\mathbb {C}_{p}$
such that the diagram with this morphism added is also commutative.
Before proving the theorem, we summarize the structure of the proof.
Step 1. By shrinking the disc, we reduce the theorem to the case where
 $\psi $
is
$\psi $
is
 $1$
-analytic.
$1$
-analytic.Step 2. Using Proposition 4.15, we convert the map
 $\varphi $
to an analytic function f on with some small
$\varphi $
to an analytic function f on with some small $$ \begin{align*} \coprod_{\mathfrak{c}\in \left[\mathrm{Cl}^{+}(F)\right]^{\left(p\right)}} \mathcal{IW}_{w,\mathfrak{c}}^{+}(v_{\mathrm{tot}})_{\mathbb{C}_{p}}\times \mathcal{D}_{\mathbb{C}_{p}}^{\times} \end{align*} $$
$$ \begin{align*} \coprod_{\mathfrak{c}\in \left[\mathrm{Cl}^{+}(F)\right]^{\left(p\right)}} \mathcal{IW}_{w,\mathfrak{c}}^{+}(v_{\mathrm{tot}})_{\mathbb{C}_{p}}\times \mathcal{D}_{\mathbb{C}_{p}}^{\times} \end{align*} $$
 $v>0$
such that locally on
$v>0$
such that locally on
 $\mathcal {D}_{\mathbb {C}_{p}}^{\times }$
it gives a normalized eigenform with eigensystem determined by
$\mathcal {D}_{\mathbb {C}_{p}}^{\times }$
it gives a normalized eigenform with eigensystem determined by
 $\varphi $
.
$\varphi $
.
Step 3. By analytic continuation via the
 $U_{p}$
-operator, we extend f to By Proposition 4.19, we may assume that f can be extended to the puncture so that it defines a normalized eigenform over
$U_{p}$
-operator, we extend f to By Proposition 4.19, we may assume that f can be extended to the puncture so that it defines a normalized eigenform over $$ \begin{align*} \coprod_{\mathfrak{c}\in \left[\mathrm{Cl}^{+}(F)\right]^{\left(p\right)}} \mathcal{IW}_{w,\mathfrak{c}}^{+}\left(\tfrac{1}{p+1}\right)_{\mathbb{C}_{p}}\times \mathcal{D}_{\mathbb{C}_{p}}^{\times}. \end{align*} $$
$$ \begin{align*} \coprod_{\mathfrak{c}\in \left[\mathrm{Cl}^{+}(F)\right]^{\left(p\right)}} \mathcal{IW}_{w,\mathfrak{c}}^{+}\left(\tfrac{1}{p+1}\right)_{\mathbb{C}_{p}}\times \mathcal{D}_{\mathbb{C}_{p}}^{\times}. \end{align*} $$
 $\mathcal {D}_{\mathbb {C}_{p}}$
.
$\mathcal {D}_{\mathbb {C}_{p}}$
.
Step 4. Using results from §3.2, we show that
 $U_{p} f$
can be evaluated on the connected neighborhood
$U_{p} f$
can be evaluated on the connected neighborhood
 $\mathcal {V}_{\mathfrak {c},Q,\mathbb {C}_{p}}^{0}$
for any critical point Q, modulo passing to a finite covering
$\mathcal {V}_{\mathfrak {c},Q,\mathbb {C}_{p}}^{0}$
for any critical point Q, modulo passing to a finite covering
 $r: \mathcal {Y}_{\mathfrak {c},p}^{1}\to \mathcal {Y}_{\mathfrak {c},p}$
.
$r: \mathcal {Y}_{\mathfrak {c},p}^{1}\to \mathcal {Y}_{\mathfrak {c},p}$
.Step 5. Supposing
 $f(O)$
is of infinite slope, we deduce a contradiction by a combinatorial argument using critical points in the spirit of Buzzard and Calegari. Then Proposition 2.7 yields a desired extension of
$f(O)$
is of infinite slope, we deduce a contradiction by a combinatorial argument using critical points in the spirit of Buzzard and Calegari. Then Proposition 2.7 yields a desired extension of
 $\varphi $
to
$\varphi $
to
 $\mathcal {D}_{\mathbb {C}_{p}}$
.
$\mathcal {D}_{\mathbb {C}_{p}}$
.
Proof.
Step 1. Let
![]() $e_{1},\dotsc ,e_{g}$
be a basis of the
$e_{1},\dotsc ,e_{g}$
be a basis of the
![]() $\mathbb {Z}_{p}$
-module
$\mathbb {Z}_{p}$
-module
![]() $2p\left (\mathcal {O}_{F}\otimes \mathbb {Z}_{p}\right )$
and put
$2p\left (\mathcal {O}_{F}\otimes \mathbb {Z}_{p}\right )$
and put
![]() $E_{i}=\exp (e_{i})\in 1+2p\left (\mathcal {O}_{F}\otimes \mathbb {Z}_{p}\right )$
. Similarly, let
$E_{i}=\exp (e_{i})\in 1+2p\left (\mathcal {O}_{F}\otimes \mathbb {Z}_{p}\right )$
. Similarly, let
![]() $e_{g+1}$
be a basis of the
$e_{g+1}$
be a basis of the
![]() $\mathbb {Z}_{p}$
-module
$\mathbb {Z}_{p}$
-module
![]() $2p\mathbb {Z}_{p}$
and put
$2p\mathbb {Z}_{p}$
and put
![]() $E_{g+1}=\exp \left (e_{g+1}\right )\in 1+2p\mathbb {Z}_{p}$
. Let
$E_{g+1}=\exp \left (e_{g+1}\right )\in 1+2p\mathbb {Z}_{p}$
. Let
![]() $(\nu ^{\mathrm {un}}, w^{\mathrm {un}})$
be the universal character on
$(\nu ^{\mathrm {un}}, w^{\mathrm {un}})$
be the universal character on
![]() $\mathcal {W}^{G}$
. Note that
$\mathcal {W}^{G}$
. Note that
 $\mathcal {W}^{G}_{\mathbb {C}_{p}}$
is the disjoint union of finitely many copies of the open unit polydisc defined by
$\mathcal {W}^{G}_{\mathbb {C}_{p}}$
is the disjoint union of finitely many copies of the open unit polydisc defined by
with parameters
![]() $X_{1},\dotsc ,X_{g+1}$
: the connected components are parametrized by the finite-order characters
$X_{1},\dotsc ,X_{g+1}$
: the connected components are parametrized by the finite-order characters
 $$ \begin{align*} \varepsilon:\mathbb{T}(\mathbb{Z}/2 p\mathbb{Z})\times (\mathbb{Z}/2 p\mathbb{Z})^{\times} \to \mathcal{O}_{\mathbb{C}_{p}}^{\times} \end{align*} $$
$$ \begin{align*} \varepsilon:\mathbb{T}(\mathbb{Z}/2 p\mathbb{Z})\times (\mathbb{Z}/2 p\mathbb{Z})^{\times} \to \mathcal{O}_{\mathbb{C}_{p}}^{\times} \end{align*} $$
and on each connected component, the point defined by
![]() $X_{i}\mapsto x_{i}$
corresponds to the character
$X_{i}\mapsto x_{i}$
corresponds to the character
![]() $(\nu ,w)$
satisfying
$(\nu ,w)$
satisfying
![]() $\nu (E_{i})=1+x_{i}$
for any
$\nu (E_{i})=1+x_{i}$
for any
![]() $i\leq g$
, and
$i\leq g$
, and
![]() $w\left (E_{g+1}\right )=1+x_{g+1}$
.
$w\left (E_{g+1}\right )=1+x_{g+1}$
.
Put
![]() $q=p$
if
$q=p$
if
![]() $p\geq 3$
and
$p\geq 3$
and
![]() $q=16$
if
$q=16$
if
![]() $p=2$
. Since
$p=2$
. Since
![]() $\psi (O)$
is
$\psi (O)$
is
![]() $1$
-integral, it comes from a K-valued point of
$1$
-integral, it comes from a K-valued point of
![]() $\mathcal {W}^{G}$
, which we also denote by
$\mathcal {W}^{G}$
, which we also denote by
![]() $\psi (O)$
. This corresponds to a finite-order character
$\psi (O)$
. This corresponds to a finite-order character
![]() $\varepsilon _{O}$
and a map
$\varepsilon _{O}$
and a map
![]() $X_{i}\mapsto x_{i}$
with some
$X_{i}\mapsto x_{i}$
with some
![]() $x_{i}\in q\mathcal {O}_{K}$
. For
$x_{i}\in q\mathcal {O}_{K}$
. For
![]() $p=2$
, the assumption that
$p=2$
, the assumption that
![]() $\psi (O)$
is
$\psi (O)$
is
![]() $1$
-doubly even implies that
$1$
-doubly even implies that
![]() $\varepsilon _{O}$
is trivial on the torsion subgroup of
$\varepsilon _{O}$
is trivial on the torsion subgroup of
![]() $1+2(\mathcal {O}_{F}\otimes \mathbb {Z}_{2})$
. Put
$1+2(\mathcal {O}_{F}\otimes \mathbb {Z}_{2})$
. Put
![]() $E^{\prime }_{i}=(-1)^{p-1}E_{i}$
. The group
$E^{\prime }_{i}=(-1)^{p-1}E_{i}$
. The group
![]() $1+p\left (\mathcal {O}_{F}\otimes \mathbb {Z}_{p}\right )$
is topologically generated by
$1+p\left (\mathcal {O}_{F}\otimes \mathbb {Z}_{p}\right )$
is topologically generated by
![]() $E_{i}$
s and
$E_{i}$
s and
![]() $E^{\prime }_{i}$
s. We have
$E^{\prime }_{i}$
s. We have
on the
![]() $\varepsilon _{O}$
-component of
$\varepsilon _{O}$
-component of
![]() $\mathcal {W}^{G}$
. Let
$\mathcal {W}^{G}$
. Let
![]() $\mathcal {U}=\mathrm {Sp}(R)$
be the admissible affinoid open subset of the
$\mathcal {U}=\mathrm {Sp}(R)$
be the admissible affinoid open subset of the
![]() $\varepsilon _{O}$
-component of
$\varepsilon _{O}$
-component of
![]() $\mathcal {W}^{G}$
defined by
$\mathcal {W}^{G}$
defined by
![]() $\lvert X_{i}-x_{i}\rvert \leq \lvert q\rvert $
for any i. Then
$\lvert X_{i}-x_{i}\rvert \leq \lvert q\rvert $
for any i. Then
![]() $1+X_{i}=1+x_{i}+(X_{i}-x_{i})\in 1+qR^{\circ }$
and the universal character
$1+X_{i}=1+x_{i}+(X_{i}-x_{i})\in 1+qR^{\circ }$
and the universal character
![]() $(\nu ^{\mathrm {un}}, w^{\mathrm {un}})$
is
$(\nu ^{\mathrm {un}}, w^{\mathrm {un}})$
is
![]() $1$
-analytic on
$1$
-analytic on
![]() $\mathcal {U}$
.
$\mathcal {U}$
.
We denote by
![]() $\mathcal {D}_{\rho ,\mathbb {C}_{p}}$
the closed disc of radius
$\mathcal {D}_{\rho ,\mathbb {C}_{p}}$
the closed disc of radius
![]() $\rho $
centered at the origin over
$\rho $
centered at the origin over
![]() $\mathbb {C}_{p}$
. Consider the element
$\mathbb {C}_{p}$
. Consider the element
![]() $\psi ^{*}(X_{i})(T)$
of the ring
$\psi ^{*}(X_{i})(T)$
of the ring
 $\mathcal {O}\left (\mathcal {D}_{\mathbb {C}_{p}}\right )=\mathbb {C}_{p}\langle T\rangle $
. Since
$\mathcal {O}\left (\mathcal {D}_{\mathbb {C}_{p}}\right )=\mathbb {C}_{p}\langle T\rangle $
. Since
![]() $\psi ^{*}(X_{i})(0)=x_{i}$
, there exists a positive rational number
$\psi ^{*}(X_{i})(0)=x_{i}$
, there exists a positive rational number
![]() $\rho <1$
such that
$\rho <1$
such that
for any i. This means
 $\psi \left (\mathcal {D}_{\rho ,\mathbb {C}_{p}}\right )\subseteq \mathcal {U}_{\mathbb {C}_{p}}$
. If we can construct a morphism
$\psi \left (\mathcal {D}_{\rho ,\mathbb {C}_{p}}\right )\subseteq \mathcal {U}_{\mathbb {C}_{p}}$
. If we can construct a morphism
![]() $\mathcal {D}_{\rho ,\mathbb {C}_{p}}\to \mathcal {E}_{\mathbb {C}_{p}}$
which makes the diagram in the theorem commutative, then by gluing we obtain the desired map
$\mathcal {D}_{\rho ,\mathbb {C}_{p}}\to \mathcal {E}_{\mathbb {C}_{p}}$
which makes the diagram in the theorem commutative, then by gluing we obtain the desired map
![]() $\mathcal {D}_{\mathbb {C}_{p}}\to \mathcal {E}_{\mathbb {C}_{p}}$
. Thus, by shrinking the disc, we may assume that
$\mathcal {D}_{\mathbb {C}_{p}}\to \mathcal {E}_{\mathbb {C}_{p}}$
. Thus, by shrinking the disc, we may assume that
![]() $\psi $
factors through
$\psi $
factors through
![]() $\mathcal {U}_{\mathbb {C}_{p}}$
.
$\mathcal {U}_{\mathbb {C}_{p}}$
.
Step 2. Put
![]() $n=1$
and
$n=1$
and
![]() $v=v_{1}$
. We may assume
$v=v_{1}$
. We may assume
![]() $v<1/(p+1)$
so that we have
$v<1/(p+1)$
so that we have
 $$ \begin{align*} \bar{\mathcal{M}}(\mu_{N},\mathfrak{c})(v_{\mathrm{tot}})\subseteq\bar{\mathcal{M}}(\mu_{N},\mathfrak{c})\left(\tfrac{1}{p+1}\right). \end{align*} $$
$$ \begin{align*} \bar{\mathcal{M}}(\mu_{N},\mathfrak{c})(v_{\mathrm{tot}})\subseteq\bar{\mathcal{M}}(\mu_{N},\mathfrak{c})\left(\tfrac{1}{p+1}\right). \end{align*} $$
By Remark 2.4, the rigid analytic variety
 $\mathcal {D}^{\times }_{\mathbb {C}_{p}}$
is principally refined. Applying Proposition 4.15 to the map
$\mathcal {D}^{\times }_{\mathbb {C}_{p}}$
is principally refined. Applying Proposition 4.15 to the map
 $\varphi : \mathcal {D}^{\times }_{\mathbb {C}_{p}}\to (\mathcal {E}\rvert _{\mathcal {U}})_{\mathbb {C}_{p}}$
, we obtain an element
$\varphi : \mathcal {D}^{\times }_{\mathbb {C}_{p}}\to (\mathcal {E}\rvert _{\mathcal {U}})_{\mathbb {C}_{p}}$
, we obtain an element
 $$ \begin{align*} f\in \bigoplus_{\mathfrak{c}\in \left[\mathrm{Cl}^{+}(F)\right]^{\left(p\right)}} \mathcal{O}\left(\mathcal{IW}_{w,\mathfrak{c}}^{+}(v_{\mathrm{tot}})_{\mathbb{C}_{p}}\times \mathcal{D}^{\times}_{\mathbb{C}_{p}}\right) \end{align*} $$
$$ \begin{align*} f\in \bigoplus_{\mathfrak{c}\in \left[\mathrm{Cl}^{+}(F)\right]^{\left(p\right)}} \mathcal{O}\left(\mathcal{IW}_{w,\mathfrak{c}}^{+}(v_{\mathrm{tot}})_{\mathbb{C}_{p}}\times \mathcal{D}^{\times}_{\mathbb{C}_{p}}\right) \end{align*} $$
and an admissible affinoid covering
 $\mathcal {D}^{\times }_{\mathbb {C}_{p}}=\bigcup _{i\in I} \mathcal {U}_{i}$
such that the restriction
$\mathcal {D}^{\times }_{\mathbb {C}_{p}}=\bigcup _{i\in I} \mathcal {U}_{i}$
such that the restriction
![]() $f\rvert _{\mathcal {U}_{i}}$
for each
$f\rvert _{\mathcal {U}_{i}}$
for each
![]() $i\in I$
is an eigenform of
$i\in I$
is an eigenform of
 $S^{G}\left (\mu _{N}, \left (\nu ^{\mathcal {U}_{i}},w^{\mathcal {U}_{i}}\right )\right )(v_{\mathrm {tot}})$
with eigensystem
$S^{G}\left (\mu _{N}, \left (\nu ^{\mathcal {U}_{i}},w^{\mathcal {U}_{i}}\right )\right )(v_{\mathrm {tot}})$
with eigensystem
 $\varphi ^{*}: \mathbf {T}\to \mathcal {O}\left (\mathcal {D}_{\mathbb {C}_{p}}^{\times }\right )\to \mathcal {O}(\mathcal {U}_{i})$
and
$\varphi ^{*}: \mathbf {T}\to \mathcal {O}\left (\mathcal {D}_{\mathbb {C}_{p}}^{\times }\right )\to \mathcal {O}(\mathcal {U}_{i})$
and
![]() $f(z)$
is normalized for any
$f(z)$
is normalized for any
 $z\in \mathcal {D}^{\times }_{\mathbb {C}_{p}}$
.
$z\in \mathcal {D}^{\times }_{\mathbb {C}_{p}}$
.
Step 3. Since
![]() $\varphi ^{*}$
comes from the eigenvariety
$\varphi ^{*}$
comes from the eigenvariety
![]() $\mathcal {E}$
, the
$\mathcal {E}$
, the
![]() $U_{p}$
-eigenvalue
$U_{p}$
-eigenvalue
![]() $\varphi ^{*}\left (U_{p}\right )\in \mathcal {O}(\mathcal {U}_{i})$
of
$\varphi ^{*}\left (U_{p}\right )\in \mathcal {O}(\mathcal {U}_{i})$
of
![]() $f\rvert _{\mathcal {U}_{i}}$
satisfies
$f\rvert _{\mathcal {U}_{i}}$
satisfies
![]() $\varphi ^{*}\left (U_{p}\right )(z)\neq 0$
for any
$\varphi ^{*}\left (U_{p}\right )(z)\neq 0$
for any
![]() $z\in \mathcal {U}_{i}\left (\mathbb {C}_{p}\right )$
, and thus we have
$z\in \mathcal {U}_{i}\left (\mathbb {C}_{p}\right )$
, and thus we have
![]() $\varphi ^{*}\left (U_{p}\right )\in \mathcal {O}(\mathcal {U}_{i})^{\times }$
. Since
$\varphi ^{*}\left (U_{p}\right )\in \mathcal {O}(\mathcal {U}_{i})^{\times }$
. Since
![]() $U_{p}$
improves the overconvergence from v to
$U_{p}$
improves the overconvergence from v to
![]() $pv$
, taking
$pv$
, taking
 $\varphi ^{*}\left (U_{p}\right )^{-1}U_{p}\left (f\rvert _{\mathcal {U}_{i}}\right )$
repeatedly we can find an eigenform
$\varphi ^{*}\left (U_{p}\right )^{-1}U_{p}\left (f\rvert _{\mathcal {U}_{i}}\right )$
repeatedly we can find an eigenform
 $$ \begin{align*} g_{i} \in S^{G}\left(\mu_{N},\left(\nu^{\mathcal{U}_{i}},w^{\mathcal{U}_{i}}\right)\right)\left(\tfrac{1}{p+1}\right) \end{align*} $$
$$ \begin{align*} g_{i} \in S^{G}\left(\mu_{N},\left(\nu^{\mathcal{U}_{i}},w^{\mathcal{U}_{i}}\right)\right)\left(\tfrac{1}{p+1}\right) \end{align*} $$
with eigensystem
 $\varphi ^{*}: \mathbf {T}\to \mathcal {O}\left (\mathcal {D}_{\mathbb {C}_{p}}^{\times }\right )\to \mathcal {O}(\mathcal {U}_{i})$
which extends
$\varphi ^{*}: \mathbf {T}\to \mathcal {O}\left (\mathcal {D}_{\mathbb {C}_{p}}^{\times }\right )\to \mathcal {O}(\mathcal {U}_{i})$
which extends
![]() $f\rvert _{\mathcal {U}_{i}}$
. Note that for any
$f\rvert _{\mathcal {U}_{i}}$
. Note that for any
![]() $z\in \mathcal {U}_{i}\left (\mathbb {C}_{p}\right )$
we have a commutative diagram
$z\in \mathcal {U}_{i}\left (\mathbb {C}_{p}\right )$
we have a commutative diagram

where the horizontal arrows are the restriction maps and the vertical arrows are the specialization maps. This implies that the specialization
![]() $g_{i}(z)$
is also nonzero for any
$g_{i}(z)$
is also nonzero for any
![]() $z\in \mathcal {U}_{i}\left (\mathbb {C}_{p}\right )$
. Since the q-expansion is determined by the restriction to the ordinary locus,
$z\in \mathcal {U}_{i}\left (\mathbb {C}_{p}\right )$
. Since the q-expansion is determined by the restriction to the ordinary locus,
![]() $g_{i}(z)$
is also normalized for any
$g_{i}(z)$
is also normalized for any
![]() $z\in \mathcal {U}_{i}\left (\mathbb {C}_{p}\right )$
. Since the Hecke eigenvalues of
$z\in \mathcal {U}_{i}\left (\mathbb {C}_{p}\right )$
. Since the Hecke eigenvalues of
![]() $g_{i}(z)$
are also given by the eigensystem
$g_{i}(z)$
are also given by the eigensystem
 $\varphi ^{*}(z): \mathbf {T}\to \mathcal {O}(\mathcal {U}_{i})\overset {z^{*}}{\to } \mathbb {C}_{p}$
, a gluing argument as in the proof of Proposition 4.15 shows that
$\varphi ^{*}(z): \mathbf {T}\to \mathcal {O}(\mathcal {U}_{i})\overset {z^{*}}{\to } \mathbb {C}_{p}$
, a gluing argument as in the proof of Proposition 4.15 shows that
![]() $g_{i}$
s can be glued. In other words, we may assume
$g_{i}$
s can be glued. In other words, we may assume
 $$ \begin{align*} f\in \bigoplus_{\mathfrak{c}\in \left[\mathrm{Cl}^{+}(F)\right]^{\left(p\right)}} \mathcal{O}\left(\mathcal{IW}^{+}_{w,\mathfrak{c}}\left(\tfrac{1}{p+1}\right)_{\mathbb{C}_{p}}\times \mathcal{D}^{\times}_{\mathbb{C}_{p}}\right). \end{align*} $$
$$ \begin{align*} f\in \bigoplus_{\mathfrak{c}\in \left[\mathrm{Cl}^{+}(F)\right]^{\left(p\right)}} \mathcal{O}\left(\mathcal{IW}^{+}_{w,\mathfrak{c}}\left(\tfrac{1}{p+1}\right)_{\mathbb{C}_{p}}\times \mathcal{D}^{\times}_{\mathbb{C}_{p}}\right). \end{align*} $$
By Proposition 4.19, we may replace f by an eigenform of the space
 $S^{G}\left (\mu _{N},\left (\nu ^{\mathcal {D}_{\mathbb {C}_{p}}},w^{\mathcal {D}_{\mathbb {C}_{p}}}\right )\right )\left (\tfrac {1}{p+1}\right )$
such that every specialization on
$S^{G}\left (\mu _{N},\left (\nu ^{\mathcal {D}_{\mathbb {C}_{p}}},w^{\mathcal {D}_{\mathbb {C}_{p}}}\right )\right )\left (\tfrac {1}{p+1}\right )$
such that every specialization on
![]() $\mathcal {D}_{\mathbb {C}_{p}}$
is normalized, which we also denote by
$\mathcal {D}_{\mathbb {C}_{p}}$
is normalized, which we also denote by
 $f=(f_{\mathfrak {c}})_{\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{\left (p\right )}}$
. By Lemma 3.13, we have an isomorphism
$f=(f_{\mathfrak {c}})_{\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{\left (p\right )}}$
. By Lemma 3.13, we have an isomorphism
 $$ \begin{align*} S^{G}\left(\mu_{N},\left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)(v_{\mathrm{tot}})\hat{\otimes}_{R,z^{*}} k(z) \simeq S^{G}\left(\mu_{N},\left(\nu^{\mathcal{D}_{\mathbb{C}_{p}}}(z),w^{\mathcal{D}_{\mathbb{C}_{p}}}(z)\right)\right)(v_{\mathrm{tot}}) \end{align*} $$
$$ \begin{align*} S^{G}\left(\mu_{N},\left(\nu^{\mathcal{U}},w^{\mathcal{U}}\right)\right)(v_{\mathrm{tot}})\hat{\otimes}_{R,z^{*}} k(z) \simeq S^{G}\left(\mu_{N},\left(\nu^{\mathcal{D}_{\mathbb{C}_{p}}}(z),w^{\mathcal{D}_{\mathbb{C}_{p}}}(z)\right)\right)(v_{\mathrm{tot}}) \end{align*} $$
for any
![]() $z\in \mathcal {D}_{\mathbb {C}_{p}}$
. Thus the map
$z\in \mathcal {D}_{\mathbb {C}_{p}}$
. Thus the map
 $\mathbf {T}\to \mathcal {O}\left (\mathcal {D}_{\mathbb {C}_{p}}\right )$
defined by the eigenvalues of f is a family of eigensystems in
$\mathbf {T}\to \mathcal {O}\left (\mathcal {D}_{\mathbb {C}_{p}}\right )$
defined by the eigenvalues of f is a family of eigensystems in
 $S^{G}\left (\mu _{N},\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )(v_{\mathrm {tot}})$
over
$S^{G}\left (\mu _{N},\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )(v_{\mathrm {tot}})$
over
![]() $\mathcal {D}_{\mathbb {C}_{p}}$
such that its restriction to
$\mathcal {D}_{\mathbb {C}_{p}}$
such that its restriction to
 $\mathcal {D}^{\times }_{\mathbb {C}_{p}}$
is
$\mathcal {D}^{\times }_{\mathbb {C}_{p}}$
is
 $\varphi ^{*}:\mathbf {T}\to \mathcal {O}\left (\mathcal {D}^{\times }_{\mathbb {C}_{p}}\right )$
. In particular, it is of finite slopes over
$\varphi ^{*}:\mathbf {T}\to \mathcal {O}\left (\mathcal {D}^{\times }_{\mathbb {C}_{p}}\right )$
. In particular, it is of finite slopes over
 $\mathcal {D}_{\mathbb {C}_{p}}^{\times }$
. If
$\mathcal {D}_{\mathbb {C}_{p}}^{\times }$
. If
![]() $f(O)$
is of finite slope, then Proposition 2.7 yields a morphism
$f(O)$
is of finite slope, then Proposition 2.7 yields a morphism
 $\mathcal {D}_{\mathbb {C}_{p}}\to \mathcal {E}\rvert _{\mathcal {U}_{\mathbb {C}_{p}}}$
with the desired property.
$\mathcal {D}_{\mathbb {C}_{p}}\to \mathcal {E}\rvert _{\mathcal {U}_{\mathbb {C}_{p}}}$
with the desired property.
Step 4. Put
![]() $\psi (O)=(\nu (O),w(O))$
and
$\psi (O)=(\nu (O),w(O))$
and
![]() $\kappa =k(\nu (O),w(O))$
, which are
$\kappa =k(\nu (O),w(O))$
, which are
![]() $1$
-integral by assumption. Let
$1$
-integral by assumption. Let
 $ \kappa _{1}=\left (k_{\beta }\right )_{\beta \in \mathbb {B}_{F}}$
be the integral weight corresponding to the restriction
$ \kappa _{1}=\left (k_{\beta }\right )_{\beta \in \mathbb {B}_{F}}$
be the integral weight corresponding to the restriction
![]() $\kappa \rvert _{\mathbb {T}^{0}_{1}\left (\mathbb {Z}_{p}\right )}$
. For any nonzero fractional ideal
$\kappa \rvert _{\mathbb {T}^{0}_{1}\left (\mathbb {Z}_{p}\right )}$
. For any nonzero fractional ideal
![]() $ \mathfrak {c}$
of F, let
$ \mathfrak {c}$
of F, let
![]() $\mathcal {X}_{\mathfrak {c}}=\mathfrak {M}(\mu _{N},\mathfrak {c})^{\mathrm {rig}}$
be the Raynaud generic fiber of the p-adic formal completion
$\mathcal {X}_{\mathfrak {c}}=\mathfrak {M}(\mu _{N},\mathfrak {c})^{\mathrm {rig}}$
be the Raynaud generic fiber of the p-adic formal completion
![]() $\mathfrak {M}(\mu _{N},\mathfrak {c})$
of
$\mathfrak {M}(\mu _{N},\mathfrak {c})$
of
![]() $M(\mu _{N},\mathfrak {c})$
. We also write
$M(\mu _{N},\mathfrak {c})$
. We also write
![]() $\mathcal {X}_{\mathfrak {c}}(v^{\prime })=\mathfrak {M}(\mu _{N},\mathfrak {c})(v^{\prime })^{\mathrm {rig}}$
for any
$\mathcal {X}_{\mathfrak {c}}(v^{\prime })=\mathfrak {M}(\mu _{N},\mathfrak {c})(v^{\prime })^{\mathrm {rig}}$
for any
![]() $v^{\prime }<1$
. For any
$v^{\prime }<1$
. For any
![]() $v^{\prime }<(p-1)/p$
and the morphism
$v^{\prime }<(p-1)/p$
and the morphism
![]() $h_{1}:\bar {\mathfrak {M}}(\Gamma _{1}(p),\mu _{N},\mathfrak {c})(v^{\prime })\to \bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(v^{\prime })$
, we put
$h_{1}:\bar {\mathfrak {M}}(\Gamma _{1}(p),\mu _{N},\mathfrak {c})(v^{\prime })\to \bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(v^{\prime })$
, we put
 $h=h_{1}^{\mathrm {rig}}$
and
$h=h_{1}^{\mathrm {rig}}$
and
![]() $\mathcal {X}_{\mathfrak {c}}^{1}(v^{\prime })=h^{-1}(\mathcal {X}_{\mathfrak {c}}(v^{\prime }))$
.
$\mathcal {X}_{\mathfrak {c}}^{1}(v^{\prime })=h^{-1}(\mathcal {X}_{\mathfrak {c}}(v^{\prime }))$
.
Consider the rigid analytic variety
![]() $\mathcal {Y}_{\mathfrak {c},p}$
as in §3.2 and the natural projection
$\mathcal {Y}_{\mathfrak {c},p}$
as in §3.2 and the natural projection
![]() $\pi :\mathcal {Y}_{\mathfrak {c},p}\to \mathcal {X}_{\mathfrak {c}}$
. Put
$\pi :\mathcal {Y}_{\mathfrak {c},p}\to \mathcal {X}_{\mathfrak {c}}$
. Put
![]() $\mathcal {Y}_{\mathfrak {c},p}(v^{\prime })=\pi ^{-1}(\mathcal {X}_{\mathfrak {c}}(v^{\prime }))$
. For the universal p-cyclic subgroup scheme
$\mathcal {Y}_{\mathfrak {c},p}(v^{\prime })=\pi ^{-1}(\mathcal {X}_{\mathfrak {c}}(v^{\prime }))$
. For the universal p-cyclic subgroup scheme
![]() $H^{\mathrm {un}}$
over
$H^{\mathrm {un}}$
over
![]() $\mathcal {Y}_{\mathfrak {c},p}$
, we put
$\mathcal {Y}_{\mathfrak {c},p}$
, we put
 $$ \begin{align*} \mathcal{Y}^{1}_{\mathfrak{c},p}=\mathrm{Isom}_{\mathcal{Y}_{\mathfrak{c},p}}\left(\mathcal{D}_{F}^{-1}\otimes \mu_{p}, H^{\mathrm{un}}\right). \end{align*} $$
$$ \begin{align*} \mathcal{Y}^{1}_{\mathfrak{c},p}=\mathrm{Isom}_{\mathcal{Y}_{\mathfrak{c},p}}\left(\mathcal{D}_{F}^{-1}\otimes \mu_{p}, H^{\mathrm{un}}\right). \end{align*} $$
We denote by r the natural projection
 $\mathcal {Y}^{1}_{\mathfrak {c},p}\to \mathcal {Y}_{\mathfrak {c},p}$
. Put
$\mathcal {Y}^{1}_{\mathfrak {c},p}\to \mathcal {Y}_{\mathfrak {c},p}$
. Put
![]() $\pi ^{1}=\pi \circ r$
and
$\pi ^{1}=\pi \circ r$
and
 $\mathcal {Y}^{1}_{\mathfrak {c},p}(v^{\prime })=\left (\pi ^{1}\right )^{-1}(\mathcal {X}_{\mathfrak {c}}(v^{\prime }))$
. We write the base extensions to
$\mathcal {Y}^{1}_{\mathfrak {c},p}(v^{\prime })=\left (\pi ^{1}\right )^{-1}(\mathcal {X}_{\mathfrak {c}}(v^{\prime }))$
. We write the base extensions to
![]() $\mathbb {C}_{p}$
of these maps also as h,
$\mathbb {C}_{p}$
of these maps also as h,
![]() $\pi $
, r, and
$\pi $
, r, and
![]() $\pi ^{1}$
, respectively. We consider
$\pi ^{1}$
, respectively. We consider
 $\mathcal {U}^{1}_{\mathfrak {c}}:=\mathcal {X}_{\mathfrak {c}}^{1}\left (\tfrac {1}{p+1}\right )$
as a Zariski open subset of
$\mathcal {U}^{1}_{\mathfrak {c}}:=\mathcal {X}_{\mathfrak {c}}^{1}\left (\tfrac {1}{p+1}\right )$
as a Zariski open subset of
 $\mathcal {Y}^{1}_{\mathfrak {c},p}\left (\tfrac {1}{p+1}\right )$
. Then we have an isomorphism
$\mathcal {Y}^{1}_{\mathfrak {c},p}\left (\tfrac {1}{p+1}\right )$
. Then we have an isomorphism
 $h^{*}\Omega ^{\kappa }\simeq \left (\pi ^{1}\right )^{*}\Omega ^{\kappa }\rvert _{\mathcal {U}^{1}_{\mathfrak {c},\mathbb {C}_{p}}}$
. Note that the sheaf
$h^{*}\Omega ^{\kappa }\simeq \left (\pi ^{1}\right )^{*}\Omega ^{\kappa }\rvert _{\mathcal {U}^{1}_{\mathfrak {c},\mathbb {C}_{p}}}$
. Note that the sheaf
![]() $h^{*}\Omega ^{\kappa }$
in this case of
$h^{*}\Omega ^{\kappa }$
in this case of
![]() $1$
-integral weight is isomorphic to the sheaf
$1$
-integral weight is isomorphic to the sheaf
![]() $h^{*}\Omega ^{\kappa _{1}}\simeq h^{*}\omega ^{\kappa _{1}} {}_{\bar {\mathcal {A}}^{\mathrm {un}},\mathbb {C}_{p}}$
as in §3.3.1. The sheaf
$h^{*}\Omega ^{\kappa _{1}}\simeq h^{*}\omega ^{\kappa _{1}} {}_{\bar {\mathcal {A}}^{\mathrm {un}},\mathbb {C}_{p}}$
as in §3.3.1. The sheaf
 $\left (\pi ^{1}\right )^{*}\Omega ^{\kappa _{1}}$
is defined over the whole rigid analytic variety
$\left (\pi ^{1}\right )^{*}\Omega ^{\kappa _{1}}$
is defined over the whole rigid analytic variety
 $\mathcal {Y}^{1}_{\mathfrak {c},p,\mathbb {C}_{p}}$
and satisfies
$\mathcal {Y}^{1}_{\mathfrak {c},p,\mathbb {C}_{p}}$
and satisfies
 $\left (\pi ^{1}\right )^{*}\Omega ^{\kappa _{1}}\rvert _{\mathcal {U}^{1}_{\mathfrak {c},\mathbb {C}_{p}}}\simeq h^{*}\Omega ^{\kappa }$
. Thus, when
$\left (\pi ^{1}\right )^{*}\Omega ^{\kappa _{1}}\rvert _{\mathcal {U}^{1}_{\mathfrak {c},\mathbb {C}_{p}}}\simeq h^{*}\Omega ^{\kappa }$
. Thus, when
![]() $\mathfrak {c}$
lies in
$\mathfrak {c}$
lies in
 $\left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
, the element
$\left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
, the element
![]() $f_{\mathfrak {c}}(O)$
defines
$f_{\mathfrak {c}}(O)$
defines
 $$ \begin{align*} g_{\mathfrak{c}}:=h^{*}f_{\mathfrak{c}}(O)=\left(\pi^{1}\right)^{*}f_{\mathfrak{c}}(O)\rvert_{\mathcal{U}^{1}_{\mathfrak{c},\mathbb{C}_{p}}}\in H^{0}\left(\mathcal{U}^{1}_{\mathfrak{c},\mathbb{C}_{p}}, \left(\pi^{1}\right)^{*}\Omega^{\kappa_{1}}(-D)\right), \end{align*} $$
$$ \begin{align*} g_{\mathfrak{c}}:=h^{*}f_{\mathfrak{c}}(O)=\left(\pi^{1}\right)^{*}f_{\mathfrak{c}}(O)\rvert_{\mathcal{U}^{1}_{\mathfrak{c},\mathbb{C}_{p}}}\in H^{0}\left(\mathcal{U}^{1}_{\mathfrak{c},\mathbb{C}_{p}}, \left(\pi^{1}\right)^{*}\Omega^{\kappa_{1}}(-D)\right), \end{align*} $$
on which any element a of the Galois group
![]() $\mathbb {T}(\mathbb {Z}/p\mathbb {Z})$
of
$\mathbb {T}(\mathbb {Z}/p\mathbb {Z})$
of
 $h:\mathcal {U}^{1}_{\mathfrak {c}}\to \mathcal {X}_{\mathfrak {c}}\left (\tfrac {1}{p+1}\right )$
acts trivially. Namely, for any point
$h:\mathcal {U}^{1}_{\mathfrak {c}}\to \mathcal {X}_{\mathfrak {c}}\left (\tfrac {1}{p+1}\right )$
acts trivially. Namely, for any point
![]() $[(A,u)]$
of
$[(A,u)]$
of
 $\mathcal {U}^{1}_{\mathfrak {c}}\left (\bar {\mathbb {Q}}_{p}\right )$
with an
$\mathcal {U}^{1}_{\mathfrak {c}}\left (\bar {\mathbb {Q}}_{p}\right )$
with an
![]() $\mathcal {O}_{F}$
-closed immersion
$\mathcal {O}_{F}$
-closed immersion
 $u:\mathcal {D}_{F}^{-1}\otimes \mu _{p}\to A$
and any
$u:\mathcal {D}_{F}^{-1}\otimes \mu _{p}\to A$
and any
![]() $a\in \mathbb {T}(\mathbb {Z}/p\mathbb {Z})$
, we have
$a\in \mathbb {T}(\mathbb {Z}/p\mathbb {Z})$
, we have
![]() $g_{\mathfrak {c}}(A,au)=g_{\mathfrak {c}}(A,u)$
.
$g_{\mathfrak {c}}(A,au)=g_{\mathfrak {c}}(A,u)$
.
Moreover, we define
 $Z^{1}_{\mathfrak {c},p}$
as the scheme over K classifying triples
$Z^{1}_{\mathfrak {c},p}$
as the scheme over K classifying triples
![]() $(A,u,D)$
consisting of an HBAV A over a base scheme over K with
$(A,u,D)$
consisting of an HBAV A over a base scheme over K with
![]() $\mathfrak {c}$
-polarization, an
$\mathfrak {c}$
-polarization, an
![]() $\mathcal {O}_{F}$
-closed immersion
$\mathcal {O}_{F}$
-closed immersion
 $u: \mathcal {D}_{F}^{-1}\otimes \mu _{p}\to A$
, and a finite flat closed
$u: \mathcal {D}_{F}^{-1}\otimes \mu _{p}\to A$
, and a finite flat closed
![]() $\mathcal {O}_{F}$
-subgroup scheme D which is étale locally isomorphic to
$\mathcal {O}_{F}$
-subgroup scheme D which is étale locally isomorphic to
![]() $\underline {\mathcal {O}_{F}/p\mathcal {O}_{F}}$
satisfying
$\underline {\mathcal {O}_{F}/p\mathcal {O}_{F}}$
satisfying
![]() $\mathrm {Im}(u)\cap D=0$
. We denote by
$\mathrm {Im}(u)\cap D=0$
. We denote by
 $\mathcal {Z}^{1}_{\mathfrak {c},p}$
the analytification of
$\mathcal {Z}^{1}_{\mathfrak {c},p}$
the analytification of
 $Z^{1}_{\mathfrak {c},p}$
restricted to
$Z^{1}_{\mathfrak {c},p}$
restricted to
![]() $\mathcal {X}_{\mathfrak {c}}$
. We have two projections
$\mathcal {X}_{\mathfrak {c}}$
. We have two projections
 $$ \begin{align*} q_{1}:\mathcal{Z}^{1}_{p^{-1}\mathfrak{c},p}&\to \mathcal{Y}^{1}_{p^{-1}\mathfrak{c},p} & q_{2}:\mathcal{Z}^{1}_{p^{-1}\mathfrak{c},p}&\to \mathcal{Y}^{1}_{\mathfrak{c},p}\\ (A,u,D)&\mapsto (A,u), & (A,u,D)&\mapsto \left(A/D,\bar{u}\right), \end{align*} $$
$$ \begin{align*} q_{1}:\mathcal{Z}^{1}_{p^{-1}\mathfrak{c},p}&\to \mathcal{Y}^{1}_{p^{-1}\mathfrak{c},p} & q_{2}:\mathcal{Z}^{1}_{p^{-1}\mathfrak{c},p}&\to \mathcal{Y}^{1}_{\mathfrak{c},p}\\ (A,u,D)&\mapsto (A,u), & (A,u,D)&\mapsto \left(A/D,\bar{u}\right), \end{align*} $$
where
![]() $\bar {u}$
is the image of u in
$\bar {u}$
is the image of u in
![]() $A/D$
. Put
$A/D$
. Put
 $\mathcal {Z}^{1}_{\mathfrak {c},p}(v^{\prime })=q_{1}^{-1}\left (\mathcal {Y}^{1}_{\mathfrak {c},p}(v^{\prime })\right )$
.
$\mathcal {Z}^{1}_{\mathfrak {c},p}(v^{\prime })=q_{1}^{-1}\left (\mathcal {Y}^{1}_{\mathfrak {c},p}(v^{\prime })\right )$
.
We denote the restriction of the rigid analytic variety
 $\mathcal {Y}^{\prime }_{\mathfrak {c},p}\left (\tfrac {1}{p+1}\right )$
defined in §3.3.3 to
$\mathcal {Y}^{\prime }_{\mathfrak {c},p}\left (\tfrac {1}{p+1}\right )$
defined in §3.3.3 to
 $\mathcal {X}_{\mathfrak {c}}\left (\tfrac {1}{p+1}\right )$
also by
$\mathcal {X}_{\mathfrak {c}}\left (\tfrac {1}{p+1}\right )$
also by
 $\mathcal {Y}^{\prime }_{\mathfrak {c},p}\left (\tfrac {1}{p+1}\right )$
. We have a finite étale morphism
$\mathcal {Y}^{\prime }_{\mathfrak {c},p}\left (\tfrac {1}{p+1}\right )$
. We have a finite étale morphism
 $$ \begin{align*} \Pi: q_{1}^{-1}\left(\mathcal{U}^{1}_{p^{-1}\mathfrak{c}}\right)\to \mathcal{Y}^{\prime}_{p^{-1}\mathfrak{c},p}\left(\tfrac{1}{p+1}\right),\quad (A,u,H)\mapsto (A,H). \end{align*} $$
$$ \begin{align*} \Pi: q_{1}^{-1}\left(\mathcal{U}^{1}_{p^{-1}\mathfrak{c}}\right)\to \mathcal{Y}^{\prime}_{p^{-1}\mathfrak{c},p}\left(\tfrac{1}{p+1}\right),\quad (A,u,H)\mapsto (A,H). \end{align*} $$
The base extensions of these maps to
![]() $\mathbb {C}_{p}$
are also denoted by
$\mathbb {C}_{p}$
are also denoted by
![]() $q_{1}$
,
$q_{1}$
,
![]() $q_{2}$
, and
$q_{2}$
, and
![]() $\Pi $
, respectively. By [Reference Hattori29, Corollary 5.3(1)], we have
$\Pi $
, respectively. By [Reference Hattori29, Corollary 5.3(1)], we have
 $q_{1}^{-1}\left (\mathcal {U}^{1}_{p^{-1}\mathfrak {c}}\right )\subseteq q_{2}^{-1}\left (\mathcal {U}^{1}_{\mathfrak {c}}\right )$
and thus
$q_{1}^{-1}\left (\mathcal {U}^{1}_{p^{-1}\mathfrak {c}}\right )\subseteq q_{2}^{-1}\left (\mathcal {U}^{1}_{\mathfrak {c}}\right )$
and thus
 $q_{1}^{-1}\left (\mathcal {U}^{1}_{p^{-1}\mathfrak {c},\mathbb {C}_{p}}\right ) \subseteq q_{2}^{-1}\left (\mathcal {U}^{1}_{\mathfrak {c},\mathbb {C}_{p}}\right )$
. This yields commutative diagrams
$q_{1}^{-1}\left (\mathcal {U}^{1}_{p^{-1}\mathfrak {c},\mathbb {C}_{p}}\right ) \subseteq q_{2}^{-1}\left (\mathcal {U}^{1}_{\mathfrak {c},\mathbb {C}_{p}}\right )$
. This yields commutative diagrams

where the latter is cartesian.
We have an isomorphism of changing polarizations
 $$ \begin{align*} l_{p}: M(\mu_{N},\mathfrak{c})\to M\left(\mu_{N},p^{-1}\mathfrak{c}\right),\quad (A,\lambda)\mapsto (A,p\lambda), \end{align*} $$
$$ \begin{align*} l_{p}: M(\mu_{N},\mathfrak{c})\to M\left(\mu_{N},p^{-1}\mathfrak{c}\right),\quad (A,\lambda)\mapsto (A,p\lambda), \end{align*} $$
which induces an isomorphism
 $\mathcal {X}_{\mathfrak {c}}\left (\tfrac {1}{p+1}\right )\to \mathcal {X}_{p^{-1}\mathfrak {c}}\left (\tfrac {1}{p+1}\right )$
and similarly for other rigid analytic varieties defined already. Let
$\mathcal {X}_{\mathfrak {c}}\left (\tfrac {1}{p+1}\right )\to \mathcal {X}_{p^{-1}\mathfrak {c}}\left (\tfrac {1}{p+1}\right )$
and similarly for other rigid analytic varieties defined already. Let
![]() $x_{\mathfrak {p}}\in F^{\times ,+}$
be the element we fixed in §3.3.3 to define
$x_{\mathfrak {p}}\in F^{\times ,+}$
be the element we fixed in §3.3.3 to define
![]() $U_{p}$
and put
$U_{p}$
and put
 $x=p^{-1}\prod _{\mathfrak {p}\mid p}x_{\mathfrak {p}}\in F^{\times ,+,(p)}$
. Then
$x=p^{-1}\prod _{\mathfrak {p}\mid p}x_{\mathfrak {p}}\in F^{\times ,+,(p)}$
. Then
![]() $l_{p}$
also induces an isomorphism
$l_{p}$
also induces an isomorphism
 $$ \begin{align*} \nu(O)(x)l_{p}^{*}: H^{0}\left(\mathcal{X}_{p^{-1}\mathfrak{c}}\left(\tfrac{1}{p+1}\right)_{\mathbb{C}_{p}},\Omega^{\kappa}\right)\to H^{0}\left(\mathcal{X}_{\mathfrak{c}}\left(\tfrac{1}{p+1}\right)_{\mathbb{C}_{p}},\Omega^{\kappa}\right), \end{align*} $$
$$ \begin{align*} \nu(O)(x)l_{p}^{*}: H^{0}\left(\mathcal{X}_{p^{-1}\mathfrak{c}}\left(\tfrac{1}{p+1}\right)_{\mathbb{C}_{p}},\Omega^{\kappa}\right)\to H^{0}\left(\mathcal{X}_{\mathfrak{c}}\left(\tfrac{1}{p+1}\right)_{\mathbb{C}_{p}},\Omega^{\kappa}\right), \end{align*} $$
which is compatible with the map
 $L_{x}\circ \prod _{\mathfrak {p}\mid p}x_{\mathfrak {p}}^{*}$
on
$L_{x}\circ \prod _{\mathfrak {p}\mid p}x_{\mathfrak {p}}^{*}$
on
 $S^{G}\left (\mu _{N},p^{-1}\mathfrak {c},(\nu (O),w(O))\right )\left (\tfrac {1}{p+1}\right )$
. Note that under the identification (4.1), by composing
$S^{G}\left (\mu _{N},p^{-1}\mathfrak {c},(\nu (O),w(O))\right )\left (\tfrac {1}{p+1}\right )$
. Note that under the identification (4.1), by composing
![]() $L_{x}$
we identify the operator
$L_{x}$
we identify the operator
![]() $U_{p}$
with a tuple of endomorphisms on
$U_{p}$
with a tuple of endomorphisms on
 $S^{G}(\mu _{N},\mathfrak {c},(\nu (O),w(O)))\left (\tfrac {1}{p+1}\right )$
for each
$S^{G}(\mu _{N},\mathfrak {c},(\nu (O),w(O)))\left (\tfrac {1}{p+1}\right )$
for each
 $\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
.
$\mathfrak {c}\in \left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
.
Take any point
![]() $Q=[(A,\mathcal {H})]\in Y_{\mathfrak {c},p}(\mathcal {O}_{L})$
with some finite extension
$Q=[(A,\mathcal {H})]\in Y_{\mathfrak {c},p}(\mathcal {O}_{L})$
with some finite extension
![]() $L/K$
such that
$L/K$
such that
![]() $\mathrm {Hdg}_{\beta }(A)=p/(p+1)$
for any
$\mathrm {Hdg}_{\beta }(A)=p/(p+1)$
for any
![]() $\beta \in \mathbb {B}_{F}$
, which exists by Lemma 3.6. Consider the admissible open subsets
$\beta \in \mathbb {B}_{F}$
, which exists by Lemma 3.6. Consider the admissible open subsets
![]() $\mathcal {V}_{\mathfrak {c},Q}$
,
$\mathcal {V}_{\mathfrak {c},Q}$
,
 $\mathcal {V}_{\mathfrak {c},Q,\mathbb {C}_{p}}^{0}$
, and
$\mathcal {V}_{\mathfrak {c},Q,\mathbb {C}_{p}}^{0}$
, and
 $\mathcal {V}_{\mathfrak {c},Q,\mathbb {C}_{p}}^{0}\left (\tfrac {1}{p+1}\right )$
of
$\mathcal {V}_{\mathfrak {c},Q,\mathbb {C}_{p}}^{0}\left (\tfrac {1}{p+1}\right )$
of
![]() $\mathcal {Y}_{\mathfrak {c},p, \mathbb {C}_{p}}$
defined in §3.2. For the point
$\mathcal {Y}_{\mathfrak {c},p, \mathbb {C}_{p}}$
defined in §3.2. For the point
![]() $l_{p}(Q)\in Y_{p^{-1}\mathfrak {c},p}(\mathcal {O}_{L})$
, we also have similar admissible open subsets
$l_{p}(Q)\in Y_{p^{-1}\mathfrak {c},p}(\mathcal {O}_{L})$
, we also have similar admissible open subsets
![]() $\mathcal {V}_{p^{-1}\mathfrak {c},l_{p}\left (Q\right )}$
,
$\mathcal {V}_{p^{-1}\mathfrak {c},l_{p}\left (Q\right )}$
,
 $\mathcal {V}_{p^{-1}\mathfrak {c},l_{p}\left (Q\right ),\mathbb {C}_{p}}^{0}$
, and
$\mathcal {V}_{p^{-1}\mathfrak {c},l_{p}\left (Q\right ),\mathbb {C}_{p}}^{0}$
, and
 $\mathcal {V}_{p^{-1} \mathfrak {c},l_{p}\left (Q\right ),\mathbb {C}_{p}}^{0}\left (\tfrac {1}{p+1}\right )$
of
$\mathcal {V}_{p^{-1} \mathfrak {c},l_{p}\left (Q\right ),\mathbb {C}_{p}}^{0}\left (\tfrac {1}{p+1}\right )$
of
![]() $\mathcal {Y}_{p^{-1}\mathfrak {c},p,\mathbb {C}_{p}}$
, which are equal to the images of
$\mathcal {Y}_{p^{-1}\mathfrak {c},p,\mathbb {C}_{p}}$
, which are equal to the images of
![]() $\mathcal {V}_{\mathfrak {c},Q}$
,
$\mathcal {V}_{\mathfrak {c},Q}$
,
 $\mathcal {V}_{\mathfrak {c},Q,\mathbb {C}_{p}}^{0}$
, and
$\mathcal {V}_{\mathfrak {c},Q,\mathbb {C}_{p}}^{0}$
, and
 $\mathcal {V}_{\mathfrak {c},Q,\mathbb {C}_{p}} {}^{0}\left (\tfrac {1}{p+1}\right )$
by
$\mathcal {V}_{\mathfrak {c},Q,\mathbb {C}_{p}} {}^{0}\left (\tfrac {1}{p+1}\right )$
by
![]() $l_{p}$
, respectively. By Corollary 3.9, we have
$l_{p}$
, respectively. By Corollary 3.9, we have
 $$ \begin{align*} q_{1}^{-1}\left(r^{-1}\left(\mathcal{V}_{p^{-1}\mathfrak{c},l_{p}\left(Q\right)}\right)\right)\subseteq q_{2}^{-1}\left(\mathcal{U}^{1}_{\mathfrak{c}}\right). \end{align*} $$
$$ \begin{align*} q_{1}^{-1}\left(r^{-1}\left(\mathcal{V}_{p^{-1}\mathfrak{c},l_{p}\left(Q\right)}\right)\right)\subseteq q_{2}^{-1}\left(\mathcal{U}^{1}_{\mathfrak{c}}\right). \end{align*} $$
Taking the base extension, we also have
 $$ \begin{align*} q_{1}^{-1}\left(r^{-1}\left(\mathcal{V}_{p^{-1}\mathfrak{c},l_{p}\left(Q\right),\mathbb{C}_{p}}^{0}\right)\right)\subseteq q_{1}^{-1}\left(r^{-1}\left(\mathcal{V}_{p^{-1}\mathfrak{c},l_{p}\left(Q\right),\mathbb{C}_{p}}\right)\right)\subseteq q_{2}^{-1}\left(\mathcal{U}^{1}_{\mathfrak{c},\mathbb{C}_{p}}\right). \end{align*} $$
$$ \begin{align*} q_{1}^{-1}\left(r^{-1}\left(\mathcal{V}_{p^{-1}\mathfrak{c},l_{p}\left(Q\right),\mathbb{C}_{p}}^{0}\right)\right)\subseteq q_{1}^{-1}\left(r^{-1}\left(\mathcal{V}_{p^{-1}\mathfrak{c},l_{p}\left(Q\right),\mathbb{C}_{p}}\right)\right)\subseteq q_{2}^{-1}\left(\mathcal{U}^{1}_{\mathfrak{c},\mathbb{C}_{p}}\right). \end{align*} $$
Similarly, Lemma 3.10 shows
 $r^{-1}\left (\mathcal {V}_{p^{-1}\mathfrak {c},l_{p}\left (Q\right ),\mathbb {C}_{p}}^{0}\left (\tfrac {1}{p+1}\right )\right )\subseteq \mathcal {U}^{1}_{p^{-1}\mathfrak {c},\mathbb {C}_{p}}$
. Since the weight
$r^{-1}\left (\mathcal {V}_{p^{-1}\mathfrak {c},l_{p}\left (Q\right ),\mathbb {C}_{p}}^{0}\left (\tfrac {1}{p+1}\right )\right )\subseteq \mathcal {U}^{1}_{p^{-1}\mathfrak {c},\mathbb {C}_{p}}$
. Since the weight
![]() $\kappa _{1}$
is integral, we have a natural isomorphism
$\kappa _{1}$
is integral, we have a natural isomorphism
 $\pi _{p}^{*}:q_{2}^{*}\left (\pi ^{1}\right )^{*}\Omega ^{\kappa _{1}} \to q_{1}^{*}\left (\pi ^{1}\right )^{*}\Omega ^{\kappa _{1}}$
over
$\pi _{p}^{*}:q_{2}^{*}\left (\pi ^{1}\right )^{*}\Omega ^{\kappa _{1}} \to q_{1}^{*}\left (\pi ^{1}\right )^{*}\Omega ^{\kappa _{1}}$
over
 $ \mathcal {Z}^{1}_{p^{-1}\mathfrak {c},p}$
. From these and the foregoing commutative diagrams, we see that the operator
$ \mathcal {Z}^{1}_{p^{-1}\mathfrak {c},p}$
. From these and the foregoing commutative diagrams, we see that the operator
![]() $U_{p}$
extends to an operator
$U_{p}$
extends to an operator
 $$ \begin{align*} U_{Q}: H^{0}\left(\mathcal{U}^{1}_{\mathfrak{c},\mathbb{C}_{p}},\left(\pi^{1}\right)^{*}\Omega^{\kappa_{1}}\right)\to H^{0}\left(r^{-1}\left(\mathcal{V}_{\mathfrak{c},Q,\mathbb{C}_{p}}^{0}\right), \left(\pi^{1}\right)^{*}\Omega^{\kappa_{1}}\right) \end{align*} $$
$$ \begin{align*} U_{Q}: H^{0}\left(\mathcal{U}^{1}_{\mathfrak{c},\mathbb{C}_{p}},\left(\pi^{1}\right)^{*}\Omega^{\kappa_{1}}\right)\to H^{0}\left(r^{-1}\left(\mathcal{V}_{\mathfrak{c},Q,\mathbb{C}_{p}}^{0}\right), \left(\pi^{1}\right)^{*}\Omega^{\kappa_{1}}\right) \end{align*} $$
which makes the following diagram commutative:

Step 5. Now suppose that
![]() $f(O)$
is of infinite slope. Then
$f(O)$
is of infinite slope. Then
 $$ \begin{align*}\left(U_{Q}g_{\mathfrak{c}}\right)\left\rvert_{r^{-1}\left(\mathcal{V}_{\mathfrak{c},Q,\mathbb{C}_{p}}^{0}\left(\tfrac{1}{p+1}\right)\right)}\right.=\left(h^{*}U_{p}f_{\mathfrak{c}}(O)\right)\left\rvert_{r^{-1}\left(\mathcal{V}_{\mathfrak{c},Q,\mathbb{C}_{p}}^{0}\left(\tfrac{1}{p+1}\right)\right)}\right.=0. \end{align*} $$
$$ \begin{align*}\left(U_{Q}g_{\mathfrak{c}}\right)\left\rvert_{r^{-1}\left(\mathcal{V}_{\mathfrak{c},Q,\mathbb{C}_{p}}^{0}\left(\tfrac{1}{p+1}\right)\right)}\right.=\left(h^{*}U_{p}f_{\mathfrak{c}}(O)\right)\left\rvert_{r^{-1}\left(\mathcal{V}_{\mathfrak{c},Q,\mathbb{C}_{p}}^{0}\left(\tfrac{1}{p+1}\right)\right)}\right.=0. \end{align*} $$
Since
 $\mathcal {V}_{\mathfrak {c},Q,\mathbb {C}_{p}}^{0}$
is connected and r is finite and étale, the map r defines a surjection from each connected component of
$\mathcal {V}_{\mathfrak {c},Q,\mathbb {C}_{p}}^{0}$
is connected and r is finite and étale, the map r defines a surjection from each connected component of
 $r^{-1} \left (\mathcal {V}_{\mathfrak {c},Q,\mathbb {C}_{p}}^{0}\right )$
to
$r^{-1} \left (\mathcal {V}_{\mathfrak {c},Q,\mathbb {C}_{p}}^{0}\right )$
to
 $\mathcal {V}_{\mathfrak {c},Q,\mathbb {C}_{p}}^{0}$
. Since the admissible open subset
$\mathcal {V}_{\mathfrak {c},Q,\mathbb {C}_{p}}^{0}$
. Since the admissible open subset
 $\mathcal {V}_{\mathfrak {c},Q,\mathbb {C}_{p}}^{0}\left (\tfrac {1}{p+1}\right )$
is nonempty, we see that
$\mathcal {V}_{\mathfrak {c},Q,\mathbb {C}_{p}}^{0}\left (\tfrac {1}{p+1}\right )$
is nonempty, we see that
 $r^{-1}\left (\mathcal {V}_{\mathfrak {c},Q,\mathbb {C}_{p}}^{0}\left (\tfrac {1}{p+1}\right )\right )$
intersects every connected component of
$r^{-1}\left (\mathcal {V}_{\mathfrak {c},Q,\mathbb {C}_{p}}^{0}\left (\tfrac {1}{p+1}\right )\right )$
intersects every connected component of
 $r^{-1}\left (\mathcal {V}_{\mathfrak {c},Q,\mathbb {C}_{p}}^{0}\right )$
. Thus Lemma 3.1 implies
$r^{-1}\left (\mathcal {V}_{\mathfrak {c},Q,\mathbb {C}_{p}}^{0}\right )$
. Thus Lemma 3.1 implies
![]() $U_{Q}g_{\mathfrak {c}}=0$
. In particular, if the point
$U_{Q}g_{\mathfrak {c}}=0$
. In particular, if the point
 $[(A,\lambda ,\mathcal {L})]\in Y_{\mathfrak {c},p}\left (\mathcal {O}_{\bar {\mathbb {Q}}_{p}}\right )$
satisfies
$[(A,\lambda ,\mathcal {L})]\in Y_{\mathfrak {c},p}\left (\mathcal {O}_{\bar {\mathbb {Q}}_{p}}\right )$
satisfies
![]() $\mathrm {Hdg}_{\beta }(A)=p/(p+1)$
for any
$\mathrm {Hdg}_{\beta }(A)=p/(p+1)$
for any
![]() $\beta \in \mathbb {B}_{F}$
, then for any
$\beta \in \mathbb {B}_{F}$
, then for any
![]() $\mathcal {O}_{F}$
-isomorphism
$\mathcal {O}_{F}$
-isomorphism
 $m: \mathcal {D}_{F}^{-1}\otimes \mu _{p}\simeq \mathcal {L}_{K}$
we have
$m: \mathcal {D}_{F}^{-1}\otimes \mu _{p}\simeq \mathcal {L}_{K}$
we have
 $$ \begin{align} \sum_{\mathcal{D}_{K}\cap \mathcal{L}_{K}=0} g_{\mathfrak{c}}\left(A/\mathcal{D}, p\bar{\lambda},\bar{m}\right)=0, \end{align} $$
$$ \begin{align} \sum_{\mathcal{D}_{K}\cap \mathcal{L}_{K}=0} g_{\mathfrak{c}}\left(A/\mathcal{D}, p\bar{\lambda},\bar{m}\right)=0, \end{align} $$
where the sum is taken over the set of finite flat closed p-cyclic
![]() $\mathcal {O}_{F}$
-subgroup schemes
$\mathcal {O}_{F}$
-subgroup schemes
![]() $\mathcal {D}$
of
$\mathcal {D}$
of
![]() $A[p]$
satisfying
$A[p]$
satisfying
![]() $\mathcal {D}_{K}\cap \mathcal {L}_{K}=0$
and
$\mathcal {D}_{K}\cap \mathcal {L}_{K}=0$
and
![]() $\bar {\lambda }$
is the induced
$\bar {\lambda }$
is the induced
![]() $p\mathfrak {c}$
-polarization. We will omit
$p\mathfrak {c}$
-polarization. We will omit
![]() $p\bar {\lambda }$
from test objects as in the foregoing.
$p\bar {\lambda }$
from test objects as in the foregoing.
Lemma 5.2. For any p-cyclic
![]() $\mathcal {O}_{F}$
-subgroup scheme
$\mathcal {O}_{F}$
-subgroup scheme
![]() $\mathcal {H}$
of
$\mathcal {H}$
of
![]() $A[p]$
and any
$A[p]$
and any
![]() $\mathcal {O}_{F}$
-isomorphism
$\mathcal {O}_{F}$
-isomorphism
 $u:\mathcal {D}_{F}^{-1}\otimes \mu _{p}\to (A[p]/\mathcal {H})_{K}$
, we have
$u:\mathcal {D}_{F}^{-1}\otimes \mu _{p}\to (A[p]/\mathcal {H})_{K}$
, we have
![]() $g_{\mathfrak {c}}(A/\mathcal {H}, u)=0$
.
$g_{\mathfrak {c}}(A/\mathcal {H}, u)=0$
.
Proof. For any p-cyclic
![]() $\mathcal {O}_{F}$
-subgroup scheme
$\mathcal {O}_{F}$
-subgroup scheme
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $A[p]$
, write
$A[p]$
, write
 $\mathcal {M}=\bigoplus _{\mathfrak {p}\mid p} \mathcal {M}_{\mathfrak {p}}$
. Similarly, any
$\mathcal {M}=\bigoplus _{\mathfrak {p}\mid p} \mathcal {M}_{\mathfrak {p}}$
. Similarly, any
![]() $\mathcal {O}_{F}$
-closed immersion
$\mathcal {O}_{F}$
-closed immersion
 $m:\mathcal {D}_{F}^{-1} \otimes \mu _{p}\to A_{K}$
defines a closed immersion
$m:\mathcal {D}_{F}^{-1} \otimes \mu _{p}\to A_{K}$
defines a closed immersion
 $m_{\mathfrak {p}}: \mathcal {D}^{-1}_{F}/\mathfrak {p}\mathcal {D}^{-1}_{F} \otimes \mu _{p} \to A[\mathfrak {p}]_{K}$
for any
$m_{\mathfrak {p}}: \mathcal {D}^{-1}_{F}/\mathfrak {p}\mathcal {D}^{-1}_{F} \otimes \mu _{p} \to A[\mathfrak {p}]_{K}$
for any
![]() $\mathfrak {p}\mid p$
. By fixing a generator of the principal
$\mathfrak {p}\mid p$
. By fixing a generator of the principal
![]() $\mathcal {O}_{F}$
-module
$\mathcal {O}_{F}$
-module
 $\mathcal {D}_{F}^{-1}/p\mathcal {D}_{F}^{-1}$
and a primitive pth root of unity in
$\mathcal {D}_{F}^{-1}/p\mathcal {D}_{F}^{-1}$
and a primitive pth root of unity in
![]() $\bar {\mathbb {Q}}_{p}$
, we identify an
$\bar {\mathbb {Q}}_{p}$
, we identify an
![]() $\mathcal {O}_{F}$
-closed immersion
$\mathcal {O}_{F}$
-closed immersion
![]() $m:\mathcal {D}^{-1} {}_{F}\otimes \mu _{p} \to A_{K}$
with an element of
$m:\mathcal {D}^{-1} {}_{F}\otimes \mu _{p} \to A_{K}$
with an element of
 $A[p]\left (\bar {\mathbb {Q}}_{p}\right )$
. Let
$A[p]\left (\bar {\mathbb {Q}}_{p}\right )$
. Let
![]() $\mathfrak {P}$
be the set of maximal ideals of
$\mathfrak {P}$
be the set of maximal ideals of
![]() $\mathcal {O}_{F}$
dividing p. For any subset
$\mathcal {O}_{F}$
dividing p. For any subset
![]() $S\subseteq \mathfrak {P}$
, we put
$S\subseteq \mathfrak {P}$
, we put
![]() $S^{c}=\mathfrak {P}\setminus S$
and
$S^{c}=\mathfrak {P}\setminus S$
and
 $$ \begin{align*} \mathcal{M}_{S}=\bigoplus_{\mathfrak{p}\in S}\mathcal{M}_{\mathfrak{p}},\qquad \mathcal{M}^{S}=\bigoplus_{\mathfrak{p}\in S^{c}} \mathcal{M}_{\mathfrak{p}},\qquad \mathcal{M}_{\emptyset}=\mathcal{M}^{\mathfrak{P}}=0. \end{align*} $$
$$ \begin{align*} \mathcal{M}_{S}=\bigoplus_{\mathfrak{p}\in S}\mathcal{M}_{\mathfrak{p}},\qquad \mathcal{M}^{S}=\bigoplus_{\mathfrak{p}\in S^{c}} \mathcal{M}_{\mathfrak{p}},\qquad \mathcal{M}_{\emptyset}=\mathcal{M}^{\mathfrak{P}}=0. \end{align*} $$
We define
![]() $m_{S}$
and
$m_{S}$
and
![]() $m^{S}$
similarly. We write
$m^{S}$
similarly. We write
![]() $\mathrm {Im}(m)$
also as
$\mathrm {Im}(m)$
also as
![]() $\langle m \rangle $
.
$\langle m \rangle $
.
For any
![]() $\mathfrak {p}\mid p$
, we fix nonzero elements
$\mathfrak {p}\mid p$
, we fix nonzero elements
 $e_{\mathfrak {p},1}\in \mathcal {H}_{\mathfrak {p}}\left (\bar {\mathbb {Q}}_{p}\right )$
and
$e_{\mathfrak {p},1}\in \mathcal {H}_{\mathfrak {p}}\left (\bar {\mathbb {Q}}_{p}\right )$
and
 $e_{\mathfrak {p},2}\in A[\mathfrak {p}]\left (\bar {\mathbb {Q}}_{p}\right )$
such that
$e_{\mathfrak {p},2}\in A[\mathfrak {p}]\left (\bar {\mathbb {Q}}_{p}\right )$
such that
![]() $\left \{e_{\mathfrak {p},1},e_{\mathfrak {p},2} \right \}$
forms a basis of the
$\left \{e_{\mathfrak {p},1},e_{\mathfrak {p},2} \right \}$
forms a basis of the
![]() $\mathfrak {o}/\mathfrak {p}$
-module
$\mathfrak {o}/\mathfrak {p}$
-module
 $A[\mathfrak {p}]\left (\bar {\mathbb {Q}}_{p}\right )$
. Put
$A[\mathfrak {p}]\left (\bar {\mathbb {Q}}_{p}\right )$
. Put
![]() $I_{\mathfrak {p}}=\left \{e_{\mathfrak {p},1}, a_{\mathfrak {p}} e_{\mathfrak {p},1}+e_{\mathfrak {p},2}\mid a_{\mathfrak {p}}\in \mathfrak {o}/\mathfrak {p}\right \}$
and
$I_{\mathfrak {p}}=\left \{e_{\mathfrak {p},1}, a_{\mathfrak {p}} e_{\mathfrak {p},1}+e_{\mathfrak {p},2}\mid a_{\mathfrak {p}}\in \mathfrak {o}/\mathfrak {p}\right \}$
and
 $e_{S,i}=\left (e_{\mathfrak {p},i}\right )_{\mathfrak {p}\in S}$
for
$e_{S,i}=\left (e_{\mathfrak {p},i}\right )_{\mathfrak {p}\in S}$
for
![]() $i=1,2$
. We claim that for any element
$i=1,2$
. We claim that for any element
![]() $m^{S}$
of
$m^{S}$
of
 $\prod _{\mathfrak {p}\in S^{c}}I_{\mathfrak {p}}$
, we have
$\prod _{\mathfrak {p}\in S^{c}}I_{\mathfrak {p}}$
, we have
 $$ \begin{align} \sum_{\mathcal{D}^{S}_{K}\cap \left\langle m^{S} \right\rangle=0}g_{\mathfrak{c}}\left(A/\left(\mathcal{H}_{S}\times \mathcal{D}^{S}\right),\overline{e_{S,2}\times m^{S}}\right)=0, \end{align} $$
$$ \begin{align} \sum_{\mathcal{D}^{S}_{K}\cap \left\langle m^{S} \right\rangle=0}g_{\mathfrak{c}}\left(A/\left(\mathcal{H}_{S}\times \mathcal{D}^{S}\right),\overline{e_{S,2}\times m^{S}}\right)=0, \end{align} $$
where the sum is taken over the set of finite flat closed
 $\left (\prod _{\mathfrak {p}\in S^{c}}\mathfrak {p}\right )$
-cyclic
$\left (\prod _{\mathfrak {p}\in S^{c}}\mathfrak {p}\right )$
-cyclic
![]() $\mathcal {O}_{F}$
-subgroup schemes
$\mathcal {O}_{F}$
-subgroup schemes
![]() $\mathcal {D}^{S}$
of A satisfying
$\mathcal {D}^{S}$
of A satisfying
 $\mathcal {D}^{S}_{K}\cap \left \langle m^{S} \right \rangle =0$
.
$\mathcal {D}^{S}_{K}\cap \left \langle m^{S} \right \rangle =0$
.
To show the claim, we proceed by induction on
![]() $\sharp S$
. The case of
$\sharp S$
. The case of
![]() $S=\emptyset $
is equation (5.1). Suppose that the claim holds for some
$S=\emptyset $
is equation (5.1). Suppose that the claim holds for some
![]() $S\neq \mathfrak {P}$
. Take
$S\neq \mathfrak {P}$
. Take
![]() $\mathfrak {p}\in S^{c}$
and put
$\mathfrak {p}\in S^{c}$
and put
![]() $S^{\prime }=S\cup \{\mathfrak {p}\}$
. Fix
$S^{\prime }=S\cup \{\mathfrak {p}\}$
. Fix
 $m^{S^{\prime }}\in \prod _{\mathfrak {q}\in (S^{\prime })^{c}}I_{\mathfrak {q}}$
. Taking the sum of equation (5.2) over the set
$m^{S^{\prime }}\in \prod _{\mathfrak {q}\in (S^{\prime })^{c}}I_{\mathfrak {q}}$
. Taking the sum of equation (5.2) over the set
 $\left \{m^{S}=m_{\mathfrak {p}} \times m^{S^{\prime }}\mid m_{\mathfrak {p}}\in I_{\mathfrak {p}}\right \}$
, we obtain
$\left \{m^{S}=m_{\mathfrak {p}} \times m^{S^{\prime }}\mid m_{\mathfrak {p}}\in I_{\mathfrak {p}}\right \}$
, we obtain
 $$ \begin{align*} \sum_{m_{\mathfrak{p}}\in I_{\mathfrak{p}}}\sum_{\mathcal{D}_{\mathfrak{p},K}\cap \left\langle m_{\mathfrak{p}} \right\rangle=0} \sum_{\mathcal{D}^{S^{\prime}}_{K}\cap \left\langle m^{S^{\prime}} \right\rangle=0}g_{\mathfrak{c}}\left(A/\left(\mathcal{H}_{S}\times \mathcal{D}_{\mathfrak{p}}\times \mathcal{D}^{S^{\prime}}\right),\overline{e_{S,2}\times m_{\mathfrak{p}}\times m^{S^{\prime}}}\right)=0. \end{align*} $$
$$ \begin{align*} \sum_{m_{\mathfrak{p}}\in I_{\mathfrak{p}}}\sum_{\mathcal{D}_{\mathfrak{p},K}\cap \left\langle m_{\mathfrak{p}} \right\rangle=0} \sum_{\mathcal{D}^{S^{\prime}}_{K}\cap \left\langle m^{S^{\prime}} \right\rangle=0}g_{\mathfrak{c}}\left(A/\left(\mathcal{H}_{S}\times \mathcal{D}_{\mathfrak{p}}\times \mathcal{D}^{S^{\prime}}\right),\overline{e_{S,2}\times m_{\mathfrak{p}}\times m^{S^{\prime}}}\right)=0. \end{align*} $$
We compute terms in this sum for each
![]() $\mathcal {D}_{\mathfrak {p}}$
.
$\mathcal {D}_{\mathfrak {p}}$
.
-
• If
 $\mathcal {D}_{\mathfrak {p}}\left (\bar {\mathbb {Q}}_{p}\right )=(\mathfrak {o}/\mathfrak {p})e_{\mathfrak {p},1}=\mathcal {H}_{\mathfrak {p}}\left (\bar {\mathbb {Q}}_{p}\right )$
and
$\mathcal {D}_{\mathfrak {p}}\left (\bar {\mathbb {Q}}_{p}\right )=(\mathfrak {o}/\mathfrak {p})e_{\mathfrak {p},1}=\mathcal {H}_{\mathfrak {p}}\left (\bar {\mathbb {Q}}_{p}\right )$
and
 $\mathcal {D}_{\mathfrak {p},K}\cap \left \langle m_{\mathfrak {p}} \right \rangle =0$
, then
$\mathcal {D}_{\mathfrak {p},K}\cap \left \langle m_{\mathfrak {p}} \right \rangle =0$
, then
 $m_{\mathfrak {p}}=a_{\mathfrak {p}} e_{\mathfrak {p},1}+e_{\mathfrak {p},2}$
with some
$m_{\mathfrak {p}}=a_{\mathfrak {p}} e_{\mathfrak {p},1}+e_{\mathfrak {p},2}$
with some
 $a_{\mathfrak {p}}\in \mathfrak {o}/\mathfrak {p}$
. In this case,
$a_{\mathfrak {p}}\in \mathfrak {o}/\mathfrak {p}$
. In this case,
 $\bar {m}_{\mathfrak {p}}$
is equal to the image
$\bar {m}_{\mathfrak {p}}$
is equal to the image
 $\bar {e}_{\mathfrak {p},2}$
of
$\bar {e}_{\mathfrak {p},2}$
of
 $e_{\mathfrak {p},2}$
.
$e_{\mathfrak {p},2}$
. -
• If
 $\mathcal {D}_{\mathfrak {p}}\left (\bar {\mathbb {Q}}_{p}\right )=(\mathfrak {o}/\mathfrak {p})\left (a_{\mathfrak {p}} e_{\mathfrak {p},1}+e_{\mathfrak {p},2}\right )$
and
$\mathcal {D}_{\mathfrak {p}}\left (\bar {\mathbb {Q}}_{p}\right )=(\mathfrak {o}/\mathfrak {p})\left (a_{\mathfrak {p}} e_{\mathfrak {p},1}+e_{\mathfrak {p},2}\right )$
and
 $\mathcal {D}_{\mathfrak {p},K}\cap \left \langle m_{\mathfrak {p}} \right \rangle =0$
, then we have either
$\mathcal {D}_{\mathfrak {p},K}\cap \left \langle m_{\mathfrak {p}} \right \rangle =0$
, then we have either
 $m_{\mathfrak {p}}=e_{\mathfrak {p}, 1}$
or
$m_{\mathfrak {p}}=e_{\mathfrak {p}, 1}$
or
 $m_{\mathfrak {p}}=b_{\mathfrak {p}} e_{\mathfrak {p},1}+e_{\mathfrak {p},2}$
with some
$m_{\mathfrak {p}}=b_{\mathfrak {p}} e_{\mathfrak {p},1}+e_{\mathfrak {p},2}$
with some
 $b_{\mathfrak {p}}\neq a_{\mathfrak {p}}\in \mathfrak {o}/\mathfrak {p}$
. In each case,
$b_{\mathfrak {p}}\neq a_{\mathfrak {p}}\in \mathfrak {o}/\mathfrak {p}$
. In each case,
 $\bar {m}_{\mathfrak {p}}$
is equal to the element
$\bar {m}_{\mathfrak {p}}$
is equal to the element
 $\bar {e}_{\mathfrak {p},1}$
or
$\bar {e}_{\mathfrak {p},1}$
or
 $\left (b_{\mathfrak {p}}-a_{\mathfrak {p}}\right )\bar {e}_{\mathfrak {p},1}$
.
$\left (b_{\mathfrak {p}}-a_{\mathfrak {p}}\right )\bar {e}_{\mathfrak {p},1}$
.
Thus the sum of the terms in which
![]() $\mathcal {D}_{\mathfrak {p}}$
s of the second case appear is equal to
$\mathcal {D}_{\mathfrak {p}}$
s of the second case appear is equal to
 $$ \begin{align*} p^{f_{\mathfrak{p}}}\sum_{\mathcal{D}^{S^{\prime}}_{K}\cap \left\langle m^{S^{\prime}} \right\rangle=0}\sum_{a_{\mathfrak{p}}\in \mathfrak{o}/\mathfrak{p}}g_{\mathfrak{c}}\left(A/\left(\mathcal{H}_{S}\times (\mathfrak{o}/\mathfrak{p})\left(a_{\mathfrak{p}} e_{\mathfrak{p},1}+e_{\mathfrak{p},2}\right)\times \mathcal{D}^{S^{\prime}}\right),\overline{e_{S,2}\times e_{\mathfrak{p},1}\times m^{S^{\prime}}}\right). \end{align*} $$
$$ \begin{align*} p^{f_{\mathfrak{p}}}\sum_{\mathcal{D}^{S^{\prime}}_{K}\cap \left\langle m^{S^{\prime}} \right\rangle=0}\sum_{a_{\mathfrak{p}}\in \mathfrak{o}/\mathfrak{p}}g_{\mathfrak{c}}\left(A/\left(\mathcal{H}_{S}\times (\mathfrak{o}/\mathfrak{p})\left(a_{\mathfrak{p}} e_{\mathfrak{p},1}+e_{\mathfrak{p},2}\right)\times \mathcal{D}^{S^{\prime}}\right),\overline{e_{S,2}\times e_{\mathfrak{p},1}\times m^{S^{\prime}}}\right). \end{align*} $$
This equals
 $$ \begin{align*} p^{f_{\mathfrak{p}}}\sum_{\mathcal{D}^{S}_{K}\cap \left\langle e_{\mathfrak{p},1}\times m^{S^{\prime}}\right\rangle=0}g_{\mathfrak{c}}\left(A/\left(\mathcal{H}_{S}\times \mathcal{D}^{S}\right), \overline{e_{S,2}\times e_{\mathfrak{p},1}\times m^{S^{\prime}}}\right), \end{align*} $$
$$ \begin{align*} p^{f_{\mathfrak{p}}}\sum_{\mathcal{D}^{S}_{K}\cap \left\langle e_{\mathfrak{p},1}\times m^{S^{\prime}}\right\rangle=0}g_{\mathfrak{c}}\left(A/\left(\mathcal{H}_{S}\times \mathcal{D}^{S}\right), \overline{e_{S,2}\times e_{\mathfrak{p},1}\times m^{S^{\prime}}}\right), \end{align*} $$
which is zero by the induction hypothesis (5.2). What remains is the sum of the terms of
![]() $\mathcal {D}_{\mathfrak {p}}$
s of the first case, which equals
$\mathcal {D}_{\mathfrak {p}}$
s of the first case, which equals
 $$ \begin{align*} p^{f_{\mathfrak{p}}}\sum_{\mathcal{D}^{S^{\prime}}_{K}\cap \left\langle m^{S^{\prime}} \right\rangle=0}g_{\mathfrak{c}}\left(A/\left(\mathcal{H}_{S^{\prime}}\times \mathcal{D}^{S^{\prime}}\right), \overline{e_{S^{\prime},2}\times m^{S^{\prime}}}\right)=0 \end{align*} $$
$$ \begin{align*} p^{f_{\mathfrak{p}}}\sum_{\mathcal{D}^{S^{\prime}}_{K}\cap \left\langle m^{S^{\prime}} \right\rangle=0}g_{\mathfrak{c}}\left(A/\left(\mathcal{H}_{S^{\prime}}\times \mathcal{D}^{S^{\prime}}\right), \overline{e_{S^{\prime},2}\times m^{S^{\prime}}}\right)=0 \end{align*} $$
and the claim follows. Setting
![]() $S=\mathfrak {P}$
, we obtain
$S=\mathfrak {P}$
, we obtain
![]() $g_{\mathfrak {c}}\left (A/\mathcal {H}, \bar {e}_{\mathfrak {P},2}\right )=0$
. For any u as in the lemma, the map
$g_{\mathfrak {c}}\left (A/\mathcal {H}, \bar {e}_{\mathfrak {P},2}\right )=0$
. For any u as in the lemma, the map
![]() $u_{\mathfrak {p}}$
corresponds to
$u_{\mathfrak {p}}$
corresponds to
![]() $a_{\mathfrak {p}} \bar {e}_{\mathfrak {p},2}$
for some
$a_{\mathfrak {p}} \bar {e}_{\mathfrak {p},2}$
for some
![]() $a_{\mathfrak {p}}\in (\mathfrak {o}/\mathfrak {p})^{\times }$
. Thus we have
$a_{\mathfrak {p}}\in (\mathfrak {o}/\mathfrak {p})^{\times }$
. Thus we have
and the lemma follows.
Consider the admissible open subset of
![]() $\mathcal {Y}_{\mathfrak {c},p}$
defined by
$\mathcal {Y}_{\mathfrak {c},p}$
defined by
 $$ \begin{align*} \left\{[(A,\lambda,\mathcal{H})]\mid \mathrm{Hdg}_{\beta}(A)=p/(p+1)\text{ for any }\beta\in\mathbb{B}_{F}\right\} \end{align*} $$
$$ \begin{align*} \left\{[(A,\lambda,\mathcal{H})]\mid \mathrm{Hdg}_{\beta}(A)=p/(p+1)\text{ for any }\beta\in\mathbb{B}_{F}\right\} \end{align*} $$
and let
![]() $\mathcal {V}$
be a nonempty admissible affinoid open subset of it. Note that the map
$\mathcal {V}$
be a nonempty admissible affinoid open subset of it. Note that the map
 $$ \begin{align*} W: \mathcal{Y}_{\mathfrak{c},p}\to \mathcal{Y}_{\mathfrak{c},p},\quad (A,\lambda,\mathcal{H})\mapsto \left(A/\mathcal{H},p\bar{\lambda},A[p]/\mathcal{H}\right) \end{align*} $$
$$ \begin{align*} W: \mathcal{Y}_{\mathfrak{c},p}\to \mathcal{Y}_{\mathfrak{c},p},\quad (A,\lambda,\mathcal{H})\mapsto \left(A/\mathcal{H},p\bar{\lambda},A[p]/\mathcal{H}\right) \end{align*} $$
is an isomorphism. By [Reference Hattori29, Proposition 6.1], we have
![]() $r^{-1}(W(\mathcal {V}))\subseteq \mathcal {U}^{1}_{\mathfrak {c}}$
. Consider the base extensions
$r^{-1}(W(\mathcal {V}))\subseteq \mathcal {U}^{1}_{\mathfrak {c}}$
. Consider the base extensions
![]() $W_{\mathbb {C}_{p}}: \mathcal {Y}_{\mathfrak {c},p, \mathbb {C}_{p}}\to \mathcal {Y}_{\mathfrak {c},p,\mathbb {C}_{p}}$
and
$W_{\mathbb {C}_{p}}: \mathcal {Y}_{\mathfrak {c},p, \mathbb {C}_{p}}\to \mathcal {Y}_{\mathfrak {c},p,\mathbb {C}_{p}}$
and
![]() $\mathcal {V}_{\mathbb {C}_{p}}$
, where the latter is an admissible affinoid open subset of
$\mathcal {V}_{\mathbb {C}_{p}}$
, where the latter is an admissible affinoid open subset of
![]() $\mathcal {Y}_{\mathfrak {c},p,\mathbb {C}_{p}}$
. By Lemma 5.2,
$\mathcal {Y}_{\mathfrak {c},p,\mathbb {C}_{p}}$
. By Lemma 5.2,
![]() $\pi ^{*}f_{\mathfrak {c}}(O)$
vanishes on the subset
$\pi ^{*}f_{\mathfrak {c}}(O)$
vanishes on the subset
 $W(\mathcal {V})\left (\bar {\mathbb {Q}}_{p}\right )$
of the admissible affinoid open subset
$W(\mathcal {V})\left (\bar {\mathbb {Q}}_{p}\right )$
of the admissible affinoid open subset
 $W_{\mathbb {C}_{p}}\left (\mathcal {V}_{\mathbb {C}_{p}}\right )=W(\mathcal {V})_{\mathbb {C}_{p}}$
.
$W_{\mathbb {C}_{p}}\left (\mathcal {V}_{\mathbb {C}_{p}}\right )=W(\mathcal {V})_{\mathbb {C}_{p}}$
.
Lemma 5.3. Let A be a reduced K-affinoid algebra. Put
![]() $X=\mathrm {Sp}(A)$
,
$X=\mathrm {Sp}(A)$
,
 $A_{\mathbb {C}_{p}}=A\hat {\otimes }_{K} \mathbb {C}_{p}$
, and
$A_{\mathbb {C}_{p}}=A\hat {\otimes }_{K} \mathbb {C}_{p}$
, and
 $X_{\mathbb {C}_{p}}=\mathrm {Sp}\left (A_{\mathbb {C}_{p}}\right )$
. We consider the set
$X_{\mathbb {C}_{p}}=\mathrm {Sp}\left (A_{\mathbb {C}_{p}}\right )$
. We consider the set
 $X\left (\bar {\mathbb {Q}}_{p}\right )$
as a subset of
$X\left (\bar {\mathbb {Q}}_{p}\right )$
as a subset of
![]() $X_{\mathbb {C}_{p}}\left (\mathbb {C}_{p}\right )$
by the natural inclusion
$X_{\mathbb {C}_{p}}\left (\mathbb {C}_{p}\right )$
by the natural inclusion
![]() $\bar {\mathbb {Q}}_{p}\to \mathbb {C}_{p}$
. Suppose that an element
$\bar {\mathbb {Q}}_{p}\to \mathbb {C}_{p}$
. Suppose that an element
![]() $f\in A_{\mathbb {C}_{p}}$
satisfies
$f\in A_{\mathbb {C}_{p}}$
satisfies
![]() $f(x)=0$
for any
$f(x)=0$
for any
 $x\in X\left (\bar {\mathbb {Q}} _{p}\right )$
. Then
$x\in X\left (\bar {\mathbb {Q}} _{p}\right )$
. Then
![]() $f=0$
.
$f=0$
.
Proof. For any positive rational number
![]() $\varepsilon $
, we put
$\varepsilon $
, we put
 $$ \begin{align*} U_{\varepsilon}=\left\{x\in X_{\mathbb{C}_{p}}\mid \lvert f(x)\rvert\leq \varepsilon\right\}. \end{align*} $$
$$ \begin{align*} U_{\varepsilon}=\left\{x\in X_{\mathbb{C}_{p}}\mid \lvert f(x)\rvert\leq \varepsilon\right\}. \end{align*} $$
We can find an element
![]() $f_{\varepsilon }\in A\otimes _{K} \bar {\mathbb {Q}}_{p}$
such that
$f_{\varepsilon }\in A\otimes _{K} \bar {\mathbb {Q}}_{p}$
such that
Then we have
 $U_{\varepsilon }=\left \{x\in X_{\mathbb {C}_{p}}\mid \lvert f_{\varepsilon }(x)\rvert \leq \varepsilon \right \}$
. Take a finite extension
$U_{\varepsilon }=\left \{x\in X_{\mathbb {C}_{p}}\mid \lvert f_{\varepsilon }(x)\rvert \leq \varepsilon \right \}$
. Take a finite extension
![]() $L/K$
satisfying
$L/K$
satisfying
![]() $f_{\varepsilon }\in A_{L}:=A\otimes _{K} L$
. Put
$f_{\varepsilon }\in A_{L}:=A\otimes _{K} L$
. Put
![]() $X_{L}=\mathrm {Sp}(A_{L})$
. The assumption implies
$X_{L}=\mathrm {Sp}(A_{L})$
. The assumption implies
 $X\left (\bar {\mathbb {Q}}_{p}\right )\subseteq U_{\varepsilon }$
, namely
$X\left (\bar {\mathbb {Q}}_{p}\right )\subseteq U_{\varepsilon }$
, namely
![]() $\lvert f_{\varepsilon }(x)\rvert \leq \varepsilon $
for any
$\lvert f_{\varepsilon }(x)\rvert \leq \varepsilon $
for any
 $x\in X\left (\bar {\mathbb {Q}} _{p}\right )$
. This shows
$x\in X\left (\bar {\mathbb {Q}} _{p}\right )$
. This shows
![]() $X_{L}=\{x\in X_{L}\mid \lvert f_{\varepsilon }(x)\rvert \leq \varepsilon \}$
. Since the formation of rational subsets is compatible with base extensions, we have
$X_{L}=\{x\in X_{L}\mid \lvert f_{\varepsilon }(x)\rvert \leq \varepsilon \}$
. Since the formation of rational subsets is compatible with base extensions, we have
![]() $X_{\mathbb {C}_{p}}=U_{\varepsilon }$
for any
$X_{\mathbb {C}_{p}}=U_{\varepsilon }$
for any
![]() $\varepsilon>0$
, which implies
$\varepsilon>0$
, which implies
![]() $f(x)=0$
for any
$f(x)=0$
for any
![]() $x\in X_{\mathbb {C}_{p}}$
. Since
$x\in X_{\mathbb {C}_{p}}$
. Since
![]() $X_{\mathbb {C}_{p}}$
is reduced, we obtain
$X_{\mathbb {C}_{p}}$
is reduced, we obtain
![]() $f=0$
and the lemma follows.
$f=0$
and the lemma follows.
Since the invertible sheaf
![]() $\pi ^{*}\Omega ^{\kappa }$
is the base extension to
$\pi ^{*}\Omega ^{\kappa }$
is the base extension to
![]() $\mathbb {C}_{p}$
of a similar invertible sheaf over K, it is trivialized by the base extension of an admissible affinoid covering over K. By Lemma 5.3, we have
$\mathbb {C}_{p}$
of a similar invertible sheaf over K, it is trivialized by the base extension of an admissible affinoid covering over K. By Lemma 5.3, we have
 $\pi ^{*}f_{\mathfrak {c}}(O)\rvert _{W(\mathcal {V})_{\mathbb {C}_{p}}}=0$
. Thus
$\pi ^{*}f_{\mathfrak {c}}(O)\rvert _{W(\mathcal {V})_{\mathbb {C}_{p}}}=0$
. Thus
![]() $f_{\mathfrak {c}}(O)$
vanishes on the admissible open subset
$f_{\mathfrak {c}}(O)$
vanishes on the admissible open subset
 $\pi \left (W(\mathcal {V})_{\mathbb {C}_{p}}\right )$
of
$\pi \left (W(\mathcal {V})_{\mathbb {C}_{p}}\right )$
of
 $\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})\left (\tfrac {1}{p+1}\right )_{\mathbb {C}_{p}}$
. By Lemma 3.4,
$\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})\left (\tfrac {1}{p+1}\right )_{\mathbb {C}_{p}}$
. By Lemma 3.4,
 $\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})\left (\tfrac {1}{p+1}\right )_{\mathbb {C}_{p}}$
is connected. By Lemma 3.1, we obtain
$\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})\left (\tfrac {1}{p+1}\right )_{\mathbb {C}_{p}}$
is connected. By Lemma 3.1, we obtain
![]() $f_{\mathfrak {c}}(O)=0$
for any
$f_{\mathfrak {c}}(O)=0$
for any
![]() $\mathfrak {c}$
, which contradicts the fact that
$\mathfrak {c}$
, which contradicts the fact that
![]() $f(O)$
is normalized. This concludes the proof of the theorem.
$f(O)$
is normalized. This concludes the proof of the theorem.
6 List of notation
Following is a list of the main notation, in order of definition.
§1:
 $\mathcal {D}_{\mathbb {C}_{p}}$
, O,
$\mathcal {D}_{\mathbb {C}_{p}}$
, O,
 $\mathcal {D}_{\mathbb {C}_{p}}^{\times }$
$\mathcal {D}_{\mathbb {C}_{p}}^{\times }$
§3.1: F, g,
 $\mathfrak {o}$
,
$\mathfrak {o}$
,
 $\mathcal {D}_{F}$
,
$\mathcal {D}_{F}$
,
 $U_{N}$
,
$U_{N}$
,
 $f_{\mathfrak {p}}$
, K, k, W,
$f_{\mathfrak {p}}$
, K, k, W,
 $\pi _{K}$
, e,
$\pi _{K}$
, e,
 $v_{p}$
,
$v_{p}$
,
 $m_{L}^{\geq i}$
,
$m_{L}^{\geq i}$
,
 $\mathcal {O}_{L,i}$
,
$\mathcal {O}_{L,i}$
,
 $\mathscr {S}_{L,i}$
,
$\mathscr {S}_{L,i}$
,
 $\mathbb {B}_{F}$
,
$\mathbb {B}_{F}$
,
 $\mathbb {B}_{\mathfrak {p}}$
,
$\mathbb {B}_{\mathfrak {p}}$
,
 $F_{\mathbb {R}}^{*}$
,
$F_{\mathbb {R}}^{*}$
,
 $F_{\mathbb {R}}^{*,+}$
,
$F_{\mathbb {R}}^{*,+}$
,
 $\mathrm {Dec}(\mathfrak {a},\mathfrak {b})$
,
$\mathrm {Dec}(\mathfrak {a},\mathfrak {b})$
,
 $\mathscr {C}(\mathfrak {a},\mathfrak {b})$
,
$\mathscr {C}(\mathfrak {a},\mathfrak {b})$
,
 $\mathscr {D}(\mathfrak {c})$
$\mathscr {D}(\mathfrak {c})$
§3.1.1:
 $\omega _{\mathcal {G},\beta }$
,
$\omega _{\mathcal {G},\beta }$
,
 $\deg _{\beta }$
,
$\deg _{\beta }$
,
 $\mathrm {Hdg}_{\beta }$
$\mathrm {Hdg}_{\beta }$
§3.1.2:
 $M(\mu _{N},\mathfrak {c})$
,
$M(\mu _{N},\mathfrak {c})$
,
 $A^{\mathrm {un}}$
,
$A^{\mathrm {un}}$
,
 $\sigma ^{\vee }$
,
$\sigma ^{\vee }$
,
 $q^{m}$
,
$q^{m}$
,
 $\hat {S}_{\sigma }$
,
$\hat {S}_{\sigma }$
,
 $\hat {R}_{\sigma }$
,
$\hat {R}_{\sigma }$
,
 $\hat {S}_{\mathscr {C}}$
,
$\hat {S}_{\mathscr {C}}$
,
 $\hat {I}_{\sigma }$
,
$\hat {I}_{\sigma }$
,
 $\bar {S}_{\sigma }$
,
$\bar {S}_{\sigma }$
,
 $\bar {S}_{\sigma }^{0}$
,
$\bar {S}_{\sigma }^{0}$
,
 $\hat {R}_{\sigma }^{0}$
,
$\hat {R}_{\sigma }^{0}$
,
 $\mathfrak {X}_{\eta }$
,
$\mathfrak {X}_{\eta }$
,
 $\mathrm {Tate}_{\mathfrak {a},\mathfrak {b}}(q)$
,
$\mathrm {Tate}_{\mathfrak {a},\mathfrak {b}}(q)$
,
 $\lambda _{\mathfrak {a},\mathfrak {b}}$
,
$\lambda _{\mathfrak {a},\mathfrak {b}}$
,
 $\bar {M}(\mu _{N},\mathfrak {c})$
, D,
$\bar {M}(\mu _{N},\mathfrak {c})$
, D,
 $\bar {A}^{\mathrm {un}}$
$\bar {A}^{\mathrm {un}}$
§3.1.3:
 $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})$
,
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})$
,
 $\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})$
,
$\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})$
,
 $\mathcal {M}(\mu _{N},\mathfrak {c})$
,
$\mathcal {M}(\mu _{N},\mathfrak {c})$
,
 $\bar {\mathfrak {A}}^{\mathrm {un}}$
,
$\bar {\mathfrak {A}}^{\mathrm {un}}$
,
 $\bar {\mathcal {A}}^{\mathrm {un}}$
,
$\bar {\mathcal {A}}^{\mathrm {un}}$
,
 $\omega _{\bar {A}^{\mathrm {un}}}$
,
$\omega _{\bar {A}^{\mathrm {un}}}$
,
 $\omega _{\bar {A}^{\mathrm {un}},\beta }$
,
$\omega _{\bar {A}^{\mathrm {un}},\beta }$
,
 $\omega _{\bar {A}^{\mathrm {un}}}^{\kappa }$
,
$\omega _{\bar {A}^{\mathrm {un}}}^{\kappa }$
,
 $\omega _{\bar {\mathcal {A}}^{\mathrm {un}},\beta }$
,
$\omega _{\bar {\mathcal {A}}^{\mathrm {un}},\beta }$
,
 $\omega _{\bar {\mathcal {A}}^{\mathrm {un}}}^{\kappa }$
,
$\omega _{\bar {\mathcal {A}}^{\mathrm {un}}}^{\kappa }$
,
 $h_{\beta }$
,
$h_{\beta }$
,
 $\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
,
$\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
,
 $\mathcal {M}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
,
$\mathcal {M}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
,
 $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
,
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
,
 $\mathfrak {M}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
,
$\mathfrak {M}(\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
,
 $\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})(v)$
,
$\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})(v)$
,
 $\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})(v_{\mathrm {tot}})$
,
$\bar {\mathcal {M}}(\mu _{N},\mathfrak {c})(v_{\mathrm {tot}})$
,
 $\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(v)$
,
$\bar {\mathfrak {M}}(\mu _{N},\mathfrak {c})(v)$
,
 $\mathbf {NAdm}$
,
$\mathbf {NAdm}$
,
 $\tau \left (\bar {P}\right )$
$\tau \left (\bar {P}\right )$
§3.1.4:
 $\mathcal {C}_{n}$
,
$\mathcal {C}_{n}$
,
 $C_{n}$
,
$C_{n}$
,
 $\mathrm {HT}_{\mathcal {G}}$
,
$\mathrm {HT}_{\mathcal {G}}$
,
 $\delta _{K}$
$\delta _{K}$
§3.2:
 $Y_{\mathfrak {c},p}$
,
$Y_{\mathfrak {c},p}$
,
 $\mathfrak {Y}_{\mathfrak {c},p}$
,
$\mathfrak {Y}_{\mathfrak {c},p}$
,
 $\mathcal {Y}_{\mathfrak {c},p}$
,
$\mathcal {Y}_{\mathfrak {c},p}$
,
 $\mathcal {V}_{\mathfrak {c},Q}$
,
$\mathcal {V}_{\mathfrak {c},Q}$
,
 $\mathcal {V}_{\mathfrak {c},Q}\left (\frac {1}{p+1}\right )$
,
$\mathcal {V}_{\mathfrak {c},Q}\left (\frac {1}{p+1}\right )$
,
 $\mathcal {V}_{\mathfrak {c},Q,\mathbb {C}_{p}}^{0}$
,
$\mathcal {V}_{\mathfrak {c},Q,\mathbb {C}_{p}}^{0}$
,
 $\mathcal {V}_{\mathfrak {c},Q,\mathbb {C}_{p}}^{0}\left (\frac {1}{p+1}\right )$
$\mathcal {V}_{\mathfrak {c},Q,\mathbb {C}_{p}}^{0}\left (\frac {1}{p+1}\right )$
§3.3.1:
 $\mathbb {T}$
,
$\mathbb {T}$
,
 $\hat {\mathbb {T}}$
,
$\hat {\mathbb {T}}$
,
 $\mathbb {T}^{0}_{w}$
,
$\mathbb {T}^{0}_{w}$
,
 $\mathcal {W}$
,
$\mathcal {W}$
,
 $\kappa ^{\mathrm {un}}$
,
$\kappa ^{\mathrm {un}}$
,
 $\mathcal {O}^{\circ }$
,
$\mathcal {O}^{\circ }$
,
 $\kappa ^{\mathcal {X}}$
,
$\kappa ^{\mathcal {X}}$
,
 $\delta _{n}$
,
$\delta _{n}$
,
 $B_{n}$
,
$B_{n}$
,
 $\bar {\mathcal {M}}(\Gamma _{1}(p^{n}),\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
,
$\bar {\mathcal {M}}(\Gamma _{1}(p^{n}),\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
,
 $\bar {\mathfrak {M}}(\Gamma _{1}(p^{n}),\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
,
$\bar {\mathfrak {M}}(\Gamma _{1}(p^{n}),\mu _{N},\mathfrak {c})\left (\underline {v}\right )$
,
 $\gamma _{w}$
,
$\gamma _{w}$
,
 $\mathfrak {IW}_{w}^{+}$
,
$\mathfrak {IW}_{w}^{+}$
,
 $\mathfrak {IW}_{w,\mathfrak {c}}^{+}\left (\underline {v}\right )$
,
$\mathfrak {IW}_{w,\mathfrak {c}}^{+}\left (\underline {v}\right )$
,
 $\mathcal {IW}_{w}^{+}$
,
$\mathcal {IW}_{w}^{+}$
,
 $\mathcal {IW}_{w,\mathfrak {c}}^{+}\left (\underline {v}\right )$
,
$\mathcal {IW}_{w,\mathfrak {c}}^{+}\left (\underline {v}\right )$
,
 $h_{w}$
,
$h_{w}$
,
 $\pi _{w}$
,
$\pi _{w}$
,
 $\mathbb {T}_{w}$
,
$\mathbb {T}_{w}$
,
 $\Omega ^{\kappa ^{\mathcal {U}}}$
,
$\Omega ^{\kappa ^{\mathcal {U}}}$
,
 $M\left (\mu _{N},\mathfrak {c},\kappa ^{\mathcal {U}}\right )\left (\underline {v}\right )$
,
$M\left (\mu _{N},\mathfrak {c},\kappa ^{\mathcal {U}}\right )\left (\underline {v}\right )$
,
 $S\left (\mu _{N},\mathfrak {c},\kappa ^{\mathcal {U}}\right )\left (\underline {v}\right )$
,
$S\left (\mu _{N},\mathfrak {c},\kappa ^{\mathcal {U}}\right )\left (\underline {v}\right )$
,
 $\mathbf {\Omega }^{\kappa ^{\mathcal {U}}}$
$\mathbf {\Omega }^{\kappa ^{\mathcal {U}}}$
§3.3.2:
 $\mathcal {W}^{G}$
,
$\mathcal {W}^{G}$
,
 $k(\nu ,w)$
,
$k(\nu ,w)$
,
 $\Delta $
,
$\Delta $
,
 $F^{\times ,+,(p)}$
,
$F^{\times ,+,(p)}$
,
 $\mathrm {Frac}(F)^{(p)}$
,
$\mathrm {Frac}(F)^{(p)}$
,
 $M^{G}\left (\mu _{N},\mathfrak {c},\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )\left (\underline {v}\right )$
,
$M^{G}\left (\mu _{N},\mathfrak {c},\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )\left (\underline {v}\right )$
,
 $S^{G}\left (\mu _{N},\mathfrak {c},\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )\left (\underline {v}\right )$
,
$S^{G}\left (\mu _{N},\mathfrak {c},\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )\left (\underline {v}\right )$
,
 $L_{x}$
,
$L_{x}$
,
 $M^{G}\left (\mu _{N},\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )\left (\underline {v}\right )$
,
$M^{G}\left (\mu _{N},\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )\left (\underline {v}\right )$
,
 $S^{G}\left (\mu _{N},\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )\left (\underline {v}\right )$
,
$S^{G}\left (\mu _{N},\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )\left (\underline {v}\right )$
,
 $M^{G}\left (\mu _{N},\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )(v_{\mathrm {tot}})$
,
$M^{G}\left (\mu _{N},\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )(v_{\mathrm {tot}})$
,
 $S^{G}\left (\mu _{N},\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )(v_{\mathrm {tot}})$
$S^{G}\left (\mu _{N},\left (\nu ^{\mathcal {U}},w^{\mathcal {U}}\right )\right )(v_{\mathrm {tot}})$
§3.3.3:
 $\mathcal {Y}^{\prime }_{\mathfrak {c},\mathfrak {l}}\left (\underline {v}\right )$
,
$\mathcal {Y}^{\prime }_{\mathfrak {c},\mathfrak {l}}\left (\underline {v}\right )$
,
 $p_{1}$
,
$p_{1}$
,
 $p_{2}$
,
$p_{2}$
,
 $\pi _{\mathfrak {l}}$
,
$\pi _{\mathfrak {l}}$
,
 $x_{\mathfrak {p}}$
,
$x_{\mathfrak {p}}$
,
 $T_{\mathfrak {l}}$
,
$T_{\mathfrak {l}}$
,
 $S_{\mathfrak {l}}$
,
$S_{\mathfrak {l}}$
,
 $U_{\mathfrak {l}}$
,
$U_{\mathfrak {l}}$
,
 $U_{p}$
,
$U_{p}$
,
 $\mathbf {T}$
,
$\mathbf {T}$
,
 $v_{n}$
,
$v_{n}$
,
 $\mathcal {E}$
$\mathcal {E}$
§3.4:
 $\pi _{w,\mathcal {O}_{\mathbb {C}_{p}}}$
,
$\pi _{w,\mathcal {O}_{\mathbb {C}_{p}}}$
,
 $\gamma _{w,\mathcal {O}_{\mathbb {C}_{p}}}$
,
$\gamma _{w,\mathcal {O}_{\mathbb {C}_{p}}}$
,
 $h_{n,\mathcal {O}_{\mathbb {C}_{p}}}$
,
$h_{n,\mathcal {O}_{\mathbb {C}_{p}}}$
,
 $\bar {M}^{*}(\mu _{N},\mathfrak {c})$
,
$\bar {M}^{*}(\mu _{N},\mathfrak {c})$
,
 $\bar {\mathfrak {M}}^{*}(\mu _{N},\mathfrak {c})(v_{\mathrm {tot}})$
,
$\bar {\mathfrak {M}}^{*}(\mu _{N},\mathfrak {c})(v_{\mathrm {tot}})$
,
 $\bar {\mathcal {M}}^{*}(\mu _{N},\mathfrak {c})(v_{\mathrm {tot}})$
,
$\bar {\mathcal {M}}^{*}(\mu _{N},\mathfrak {c})(v_{\mathrm {tot}})$
,
 $\rho $
,
$\rho $
,
 $\rho ^{\mathrm {rig}}$
,
$\rho ^{\mathrm {rig}}$
,
 $\rho _{\mathcal {O}_{\mathbb {C}_{p}}}$
,
$\rho _{\mathcal {O}_{\mathbb {C}_{p}}}$
,
 $\rho ^{\mathrm {rig}}_{\mathbb {C}_{p}}$
$\rho ^{\mathrm {rig}}_{\mathbb {C}_{p}}$
§4:
 $\left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
,
$\left [\mathrm {Cl}^{+}(F)\right ]^{(p)}$
,
 $f_{\mathfrak {c}}$
$f_{\mathfrak {c}}$
§4.1:
 $\breve {S}_{\sigma }$
,
$\breve {S}_{\sigma }$
,
 $\breve {R}_{\sigma }$
,
$\breve {R}_{\sigma }$
,
 $\mathcal {O}_{L}\left [X_{\leq r},X^{\pm }_{>r}\right ]$
,
$\mathcal {O}_{L}\left [X_{\leq r},X^{\pm }_{>r}\right ]$
,
 $\mathcal {O}_{L}\left \langle X_{\leq r},X^{\pm }_{>r}\right \rangle $
,
$\mathcal {O}_{L}\left \langle X_{\leq r},X^{\pm }_{>r}\right \rangle $
,
 $L\left \langle X_{\leq r},X^{\pm }_{>r}\right \rangle $
,
$L\left \langle X_{\leq r},X^{\pm }_{>r}\right \rangle $
,
 $\breve {S}^{\mathrm {rig}}_{\sigma }$
,
$\breve {S}^{\mathrm {rig}}_{\sigma }$
,
 $\breve {S}_{\mathscr {C}}$
,
$\breve {S}_{\mathscr {C}}$
,
 $\breve {S}^{\mathrm {rig}}_{\mathscr {C}}$
,
$\breve {S}^{\mathrm {rig}}_{\mathscr {C}}$
,
 $(-)^{\mathrm {rig}}_{/\mathbb {C}_{p}}$
,
$(-)^{\mathrm {rig}}_{/\mathbb {C}_{p}}$
,
 $\breve {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
,
$\breve {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
,
 $\breve {S}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
,
$\breve {S}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
,
 $\breve {S}_{\mathscr {C},\mathcal {O}_{\mathbb {C}_{p}}}$
,
$\breve {S}_{\mathscr {C},\mathcal {O}_{\mathbb {C}_{p}}}$
,
 $\tilde {S}_{\sigma }$
,
$\tilde {S}_{\sigma }$
,
 $\tilde {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
,
$\tilde {R}_{\sigma ,\mathcal {O}_{\mathbb {C}_{p}}}$
,
 $\tau _{\mathfrak {a},\mathfrak {b}}$
,
$\tau _{\mathfrak {a},\mathfrak {b}}$
,
 $\mathcal {O}_{\mathcal {K}_{\sigma }}$
,
$\mathcal {O}_{\mathcal {K}_{\sigma }}$
,
 $f_{\mathfrak {c}}(q)$
,
$f_{\mathfrak {c}}(q)$
,
 $a_{\mathfrak {o},\mathfrak {c}^{-1}}(f,\xi )$
$a_{\mathfrak {o},\mathfrak {c}^{-1}}(f,\xi )$
§4.2:
 $\Lambda (\mathfrak {n})$
,
$\Lambda (\mathfrak {n})$
,
 $\Phi (\mathfrak {n})$
,
$\Phi (\mathfrak {n})$
,
 $\mu _{\mathfrak {n}}$
,
$\mu _{\mathfrak {n}}$
,
 $\zeta ^{\eta }$
$\zeta ^{\eta }$
§4.2.1:
 $\hat {R}_{\eta ,\sigma }$
,
$\hat {R}_{\eta ,\sigma }$
,
 $\hat {R}^{0}_{\eta ,\sigma }$
,
$\hat {R}^{0}_{\eta ,\sigma }$
,
 $\breve {R}_{\eta ,\sigma }$
,
$\breve {R}_{\eta ,\sigma }$
,
 $q^{\eta }$
,
$q^{\eta }$
,
 $\mathrm {Tate}_{\mathfrak {a},\mathfrak {b}}(q^{\eta })$
$\mathrm {Tate}_{\mathfrak {a},\mathfrak {b}}(q^{\eta })$
§4.3:
 $\mathbf {M}(\mu _{N},\mathfrak {c},\kappa )(0)$
,
$\mathbf {M}(\mu _{N},\mathfrak {c},\kappa )(0)$
,
 $\mathcal {S}_{\mathfrak {c}}$
$\mathcal {S}_{\mathfrak {c}}$
§4.4:
 $a_{\mathfrak {o},\mathfrak {o}}^{\mathcal {U}}(f,1)$
$a_{\mathfrak {o},\mathfrak {o}}^{\mathcal {U}}(f,1)$
§5:
 $\mathcal {U}$
,
$\mathcal {U}$
,
 $\mathcal {X}_{\mathfrak {c}}$
,
$\mathcal {X}_{\mathfrak {c}}$
,
 $\mathcal {X}_{\mathfrak {c}}(v^{\prime })$
, h,
$\mathcal {X}_{\mathfrak {c}}(v^{\prime })$
, h,
 $\mathcal {X}^{1}_{\mathfrak {c}}(v^{\prime })$
,
$\mathcal {X}^{1}_{\mathfrak {c}}(v^{\prime })$
,
 $\mathcal {Y}_{\mathfrak {c},p}(v^{\prime })$
, r,
$\mathcal {Y}_{\mathfrak {c},p}(v^{\prime })$
, r,
 $\mathcal {Y}^{1}_{\mathfrak {c},p}$
,
$\mathcal {Y}^{1}_{\mathfrak {c},p}$
,
 $\pi ^{1}$
,
$\pi ^{1}$
,
 $\mathcal {Y}^{1}_{\mathfrak {c},p}(v^{\prime })$
,
$\mathcal {Y}^{1}_{\mathfrak {c},p}(v^{\prime })$
,
 $\mathcal {U}^{1}_{\mathfrak {c}}$
,
$\mathcal {U}^{1}_{\mathfrak {c}}$
,
 $g_{\mathfrak {c}}$
,
$g_{\mathfrak {c}}$
,
 $Z_{\mathfrak {c},p}$
,
$Z_{\mathfrak {c},p}$
,
 $\mathcal {Z}_{\mathfrak {c},p}$
,
$\mathcal {Z}_{\mathfrak {c},p}$
,
 $q_{1}$
,
$q_{1}$
,
 $q_{2}$
,
$q_{2}$
,
 $\mathcal {Z}_{\mathfrak {c},p}(v^{\prime })$
,
$\mathcal {Z}_{\mathfrak {c},p}(v^{\prime })$
,
 $\Pi $
$\Pi $
Acknowledgments
The author would like to thank Fabrizio Andreatta, Ruochuan Liu, and Vincent Pilloni for kindly answering his questions on their works. He is also grateful to Kevin Buzzard, Yoichi Mieda, Tomoki Mihara, Tadashi Ochiai, Vincent Pilloni, and Yuichiro Taguchi for stimulating comments on an earlier draft, and the anonymous referee for valuable comments. He also would like to thank Shu Sasaki for enlightening discussions on p-adic modular forms and encouragements.
This work was supported by JSPS KAKENHI grant numbers JP26400016, JP20K03545.
Competing Interests
None.