Article contents
THE LOEWY STRUCTURE OF 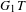 $G_{1}T$-VERMA MODULES OF SINGULAR HIGHEST WEIGHTS
$G_{1}T$-VERMA MODULES OF SINGULAR HIGHEST WEIGHTS
Published online by Cambridge University Press: 02 October 2015
Abstract
Let 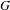 $G$ be a reductive algebraic group over an algebraically closed field of positive characteristic,
$G$ be a reductive algebraic group over an algebraically closed field of positive characteristic, 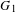 $G_{1}$ the Frobenius kernel of
$G_{1}$ the Frobenius kernel of 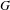 $G$, and
$G$, and  $T$ a maximal torus of
$T$ a maximal torus of 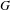 $G$. We show that the parabolically induced
$G$. We show that the parabolically induced  $G_{1}T$-Verma modules of singular highest weights are all rigid, determine their Loewy length, and describe their Loewy structure using the periodic Kazhdan–Lusztig
$G_{1}T$-Verma modules of singular highest weights are all rigid, determine their Loewy length, and describe their Loewy structure using the periodic Kazhdan–Lusztig  $P$- and
$P$- and 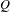 $Q$-polynomials. We assume that the characteristic of the field is sufficiently large that, in particular, Lusztig’s conjecture for the irreducible
$Q$-polynomials. We assume that the characteristic of the field is sufficiently large that, in particular, Lusztig’s conjecture for the irreducible 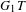 $G_{1}T$-characters holds.
$G_{1}T$-characters holds.
MSC classification
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 16 , Issue 4 , September 2017 , pp. 887 - 898
- Copyright
- © Cambridge University Press 2015
References
- 1
- Cited by


