Hostname: page-component-76fb5796d-qxdb6 Total loading time: 0 Render date: 2024-04-25T13:27:04.263Z Has data issue: false hasContentIssue false
  • English
  • Français

THE DOUBLE COVER OF ODD GENERAL SPIN GROUPS, SMALL REPRESENTATIONS, AND APPLICATIONS

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  07 August 2015

Eyal Kaplan
Eyal Kaplan*
Affiliation:
Department of Mathematics, Weizmann Institute of Science, Rehovot 7632700, Israel (kaplaney@gmail.com)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We construct local and global metaplectic double covers of odd general spin groups, using the cover of Matsumoto of spin groups. Following Kazhdan and Patterson, a local exceptional representation is the unique irreducible quotient of a principal series representation, induced from a certain exceptional character. The global exceptional representation is obtained as the multi-residue of an Eisenstein series: it is an automorphic representation, and it decomposes as the restricted tensor product of local exceptional representations. As in the case of the small representation of 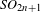$\mathit{SO}_{2n+1}$ of Bump, Friedberg, and Ginzburg, exceptional representations enjoy the vanishing of a large class of twisted Jacquet modules (locally), or Fourier coefficients (globally). Consequently they are useful in many settings, including lifting problems and Rankin–Selberg integrals. We describe one application, to a calculation of a co-period integral.

Keywords

small representationsmetaplectic coverGSpin groupsco-period integral

MSC classification

Primary: 11F70: Representation-theoretic methods; automorphic representations over local and global fields
Secondary: 11F27: Theta series; Weil representation; theta correspondences
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 16 , Issue 3 , June 2017 , pp. 609 - 671
Copyright
© Cambridge University Press 2015 

References

Arthur, J. G., A trace formula for reductive groups. I. Terms associated to classes in G (Q), Duke Math. J. 45(4) (1978), 911–952.Google Scholar
Arthur, J., A trace formula for reductive groups. II. Applications of a truncation operator, Compos. Math. 40(1) (1980), 87–121.Google Scholar
Arthur, J., Unipotent automorphic representations: conjectures, Astérisque 171–172 (1989), 13–71. Orbites unipotentes et représentations, II.Google Scholar
Asgari, M., On holomorphy of local Langlands L-functions, ProQuest LLC, Ann Arbor, MI, PhD thesis, Purdue University (2000).Google Scholar
Asgari, M., Local L-functions for split spinor groups, Canad. J. Math. 54(4) (2002), 673–693.Google Scholar
Asgari, M. and Shahidi, F., Generic transfer for general spin groups, Duke Math. J. 132(1) (2006), 137–190.Google Scholar
Asgari, M. and Shahidi, F., Image of functoriality for general spin groups, Manuscripta Math. 144 (2014), 609–638.CrossRefGoogle Scholar
Ban, D. and Jantzen, C., The Langlands quotient theorem for finite central extensions of p-adic groups, Glas. Mat. Ser. III 48(2) (2013), 313–334.Google Scholar
Banks, W., A corollary to Bernstein’s theorem and Whittaker functionals on the metaplectic group, Math. Res. Lett. 5(6) (1998), 781–790.CrossRefGoogle Scholar
Banks, W. D., Levy, J. and Sepanski, M. R., Block-compatible metaplectic cocycles, J. Reine Angew. Math. 1999(507) (1999), 131–163.CrossRefGoogle Scholar
Bernstein, I. N. and Zelevinsky, A. V., Representations of the group GL (n, F) where F is a local non-Archimedean field, Russian Math. Surveys 31(3) (1976), 1–68.CrossRefGoogle Scholar
Bernstein, I. N. and Zelevinsky, A. V., Induced representations of reductive p-adic groups I, Ann. Sci. Éc. Norm. Supér. (4) 10(4) (1977), 441–472.Google Scholar
Borel, A. and Wallach, N. R., Continuous Cohomology, Discrete Subgroups, and Representations of Reductive Groups, Annals of Mathematics Studies, Volume 94 (Princeton University Press, Princeton, NJ, 1980).Google Scholar
Brylinski, J.-L. and Deligne, P., Central extensions of reductive groups by K 2 , Publ. Math. Inst. Hautes Études Sci. 94(1) (2001), 5–85.Google Scholar
Brylinski, R. and Kostant, B., Minimal representations of E 6 , E 7 , and E 8 and the generalized Capelli identity, Proc. Natl. Acad. Sci. USA 91(7) (1994), 2469–2472.Google Scholar
Bump, D., Friedberg, S. and Ginzburg, D., A Rankin–Selberg integral using the automorphic minimal representation of SO (7), J. Ramanujan Math. Soc. 15(2) (2000), 81–124.Google Scholar
Bump, D., Friedberg, S. and Ginzburg, D., Small representations for odd orthogonal groups, Int. Math. Res. Not. IMRN 2003(25) (2003), 1363–1393.CrossRefGoogle Scholar
Bump, D., Friedberg, S. and Ginzburg, D., Lifting automorphic representations on the double covers of orthogonal groups, Duke Math. J. 131(2) (2006), 363–396.CrossRefGoogle Scholar
Bump, D. and Ginzburg, D., Symmetric square L-functions on GL(r), Ann. of Math. (2) 136(1) (1992), 137–205.CrossRefGoogle Scholar
Carter, R. W., Finite groups of Lie type, in Wiley Classics Library (John Wiley & Sons Ltd., Chichester, 1993). Conjugacy classes and complex characters, Reprint of the 1985 original, A Wiley-Interscience Publication.Google Scholar
Casselman, W., The unramified principal series of p-adic groups I: the spherical function, Compos. Math. 40(3) (1980), 387–406.Google Scholar
Collingwood, D. H. and McGovern, W. M., Nilpotent Orbits in Semisimple Lie Algebras, Van Nostrand Reinhold Mathematics Series (Van Nostrand Reinhold Co., New York, 1993).Google Scholar
Finkelberg, M. and Lysenko, S., Twisted geometric Satake equivalence, J. Inst. Math. Jussieu 9(4) (2010), 719–739.CrossRefGoogle Scholar
Flicker, Y. Z. and Kazhdan, D. A., Metaplectic correspondence, Publ. Math. Inst. Hautes Études Sci. 64(1) (1986), 53–110.Google Scholar
Flicker, Y., Kazhdan, D. and Savin, G., Explicit realization of a metaplectic representation, J. Anal. Math. 55(1) (1990), 17–39.Google Scholar
Gan, W. T. and Savin, G., On minimal representations definitions and properties, Represent. Theory 9 (2005), 46–93 (electronic).Google Scholar
Ginzburg, D., Certain conjectures relating unipotent orbits to automorphic representations, Israel J. Math. 151(1) (2006), 323–355.CrossRefGoogle Scholar
Ginzburg, D., Jiang, D. and Rallis, S., Nonvanishing of the central critical value of the third symmetric power L-functions, Forum Math. 13(1) (2001), 109–132.CrossRefGoogle Scholar
Ginzburg, D., Jiang, D. and Soudry, D., Periods of automorphic forms, poles of L-functions and functorial lifting, Sci. China Math. 53(9) (2010), 2215–2238.CrossRefGoogle Scholar
Ginzburg, D., Jiang, D. and Soudry, D., On certain automorphic descents to GL2 , Int. Math. Res. Not. IMRN 2011(21) (2011), 4779–4820.Google Scholar
Ginzburg, D., Rallis, S. and Soudry, D., On the automorphic theta representation for simply laced groups, Israel J. Math. 100(1) (1997), 61–116.Google Scholar
Ginzburg, D., Rallis, S. and Soudry, D., On a correspondence between cuspidal representations of GL 2n and ˜Sp 2n , J. Amer. Math. Soc. 12(3) (1999), 849–907.Google Scholar
Ginzburg, D., Rallis, S. and Soudry, D., On explicit lifts of cusp forms from GL m to classical groups, Ann. of Math. (2) 150(3) (1999), 807–866.Google Scholar
Ginzburg, D., Rallis, S. and Soudry, D., Generic automorphic forms on SO (2n + 1): functorial lift to GL (2n), endoscopy, and base change, Int. Math. Res. Not. IMRN 2001(14) (2001), 729–764.CrossRefGoogle Scholar
Ginzburg, D., Rallis, S. and Soudry, D., On Fourier coefficients of automorphic forms of symplectic groups, Manuscripta Math. 111(1) (2003), 1–16.CrossRefGoogle Scholar
Ginzburg, D., Rallis, S. and Soudry, D., The Descent Map from Automorphic Representations of GL(n) to Classical Groups (World Scientific Publishing, Singapore, 2011).Google Scholar
Hundley, J. and Sayag, E., Descent construction for GSpin groups, Mem. Amer. Math. Soc. (to appear) Preprint, 2012, arXiv:1110.6788v2 [math.NT].Google Scholar
Ikeda, T., On the theory of Jacobi forms and Fourier–Jacobi coefficients of Eisenstein series, J. Math. Kyoto Univ. 34(3) (1994), 615–636.Google Scholar
Jacquet, H. and Rallis, S., Symplectic periods, J. Reine Angew. Math. 1992(423) (1992), 175–197.Google Scholar
Jiang, D., G 2 -periods and residual representations, J. Reine Angew. Math. 497 (1998), 17–46.Google Scholar
Jiang, D. and Soudry, D., The local converse theorem for SO (2n + 1) and applications, Ann. of Math. (2) 157(3) (2003), 743–806.Google Scholar
Kable, A. C., The tensor product of exceptional representations on the general linear group, Ann. Sci. Éc. Norm. Supér. (4) 34(5) (2001), 741–769.CrossRefGoogle Scholar
Kaplan, E., On the local theory of Rankin–Selberg convolutions for $\mathit{SO}_{2l}\times \mathit{GL}_{n}$ , Thesis, Tel-Aviv University, Israel (2013).Google Scholar
Kaplan, E., The characterization of theta-distinguished representations of $GL_{n}$ , Preprint, 2015, arXiv:1502.06643 [math.RT].Google Scholar
Kaplan, E., The theta period of a cuspidal automorphic representation of GL (n), Int. Math. Res. Not. IMRN 2015(8) (2015), 2168–2209.Google Scholar
Kazhdan, D., The minimal representation of D 4 , in Operator Algebras, Unitary Representations, Enveloping Algebras, and Invariant Theory (Paris, 1989), Progress in Mathematics, Volume 92, pp. 125–158 (Birkhäuser Boston, Boston, MA, 1990).Google Scholar
Kazhdan, D. A. and Patterson, S. J., Metaplectic forms, Publ. Math. Inst. Hautes Études Sci. 59(1) (1984), 35–142.Google Scholar
Kazhdan, D., Pioline, B. and Waldron, A., Minimal representations, spherical vectors and exceptional theta series, Comm. Math. Phys. 226(1) (2002), 1–40.Google Scholar
Kazhdan, D. and Savin, G., The smallest representation of simply laced groups, in Festschrift in Honor of I. I. Piatetski–Shapiro on the Occasion of his Sixtieth Birthday, Part I (Ramat Aviv, 1989), Israel Mathematical Conference Proceedings, Volume 2, pp. 209–223 (Weizmann, Jerusalem, 1990).Google Scholar
Kim, H. H. and Kim, W., On local L-functions and normalized intertwining operators II; quasi-split groups, in On Certain L-functions, Clay Mathematics Proceedings, Volume 13, pp. 265–295 (American Mathematical Society, Providence, RI, 2011).Google Scholar
Kubota, T., Topological covering of SL (2) over a local field, J. Math. Soc. Japan 19(1) (1967), 114–121.Google Scholar
Kubota, T., On Automorphic Functions and the Reciprocity Law in a Number Field, Lectures in Mathematics (Department of Mathematics, Kyoto University, No. 2. Kinokuniya Book-Store Co. Ltd., Tokyo, 1969).Google Scholar
Labesse, J.-P. and Waldspurger, J.-L., La formule des traces tordue d’après le Friday Morning Seminar, in CRM Monograph Series, Volume 31 (American Mathematical Society, Providence, RI and Centre de Recherches Mathématiques, Montréal, 2013).Google Scholar
Langlands, R. P., On the classification of irreducible representations of real algebraic groups, in Representation Theory and Harmonic Analysis on Semisimple Lie Groups, Mathematical Surveys and Monographs, Volume 31, pp. 101–170 (American Mathematical Society, Providence, RI, 1989).Google Scholar
Lapid, E. and Mao, Z., A conjecture on Whittaker–Fourier coefficients of cusp forms, J. Number Theory 146 (2015), 448–505.Google Scholar
Loke, H. Y. and Savin, G., On minimal representations of Chevalley groups of type D n , E n and G 2 , Math. Ann. 340(1) (2008), 195–208.Google Scholar
Loke, H. Y. and Savin, G., Modular forms on non-linear double covers of algebraic groups, Trans. Amer. Math. Soc. 362(9) (2010), 4901–4920.Google Scholar
Matić, I., Levi subgroups of p-adic Spin (2n + 1), Math. Commun. 14(2) (2009), 223–233.Google Scholar
Matsumoto, H., Sur les sous-groupes arithmétiques des groupes semi-simples déployés, Ann. Sci. Éc. Norm. Supér. (4) 2(1) (1969), 1–62.Google Scholar
McNamara, P. J., Metaplectic Whittaker functions and crystal bases, Duke Math. J. 156(1) (2011), 1–31.Google Scholar
McNamara, P. J., Principal series representations of metaplectic groups over local fields, in Multiple Dirichlet Series, L-functions and Automorphic Forms, Progress in Mathematics, Volume 300, pp. 299–327 (Birkhäuser/Springer, New York, 2012).Google Scholar
Mezo, P., Metaplectic tensor products for irreducible representations, Pacific J. Math. 215(1) (2004), 85–96.Google Scholar
Mœglin, C. and Waldspurger, J.-L., Spectral Decomposition and Eisenstein Series (Cambridge University Press, New York, 1995).Google Scholar
Moore, C. C., Group extensions of p-adic and adelic linear groups, Publ. Math. Inst. Hautes Études Sci. 35(1) (1968), 157–222.Google Scholar
Muić, G., A geometric construction of intertwining operators for reductive p-adic groups, Manuscripta Math. 125 (2008), 241–272.CrossRefGoogle Scholar
Perrin, P., Représentations de Schrödinger, indice de Maslov et groupe metaplectique, in Non Commutative Harmonic Analysis and Lie Groups (Proc. Marseille-Luminy 1980), Lecture Notes in Mathematics, Volume 880, pp. 370–407 (Springer, Berlin–New York, 1981).Google Scholar
Prasad, D., Weil representation, Howe duality, and the theta correspondence, in Theta Functions: From the Classical to the Modern, CRM Proceedings & Lecture Notes, Volume 1, pp. 105–127 (American Mathematical Society, Providence, RI, 1993).Google Scholar
Rao, R., On some explicit formulas in the theory of Weil representations, Pacific J. Math. 157(2) (1993), 335–371.Google Scholar
Roskies, J. R., The Minimal Representation of SO (4, 3) Over a P-adic Field (Stanford University, California, 1996).Google Scholar
Sabourin, H., Une représentation unipotente associée à l’orbite minimale: le cas de SO (4, 3), J. Funct. Anal. 137(2) (1996), 394–465.Google Scholar
Savin, G., An analogue of the Weil representation for G 2 , J. Reine Angew. Math.(434) (1993), 115–126.Google Scholar
Savin, G., Dual pair G J ×PGL2 , G J is the automorphism group of the Jordan algebra J, Invent. Math. 118(1) (1994), 141–160.Google Scholar
Silberger, A. J., Introduction to Harmonic Analysis on Reductive p-adic Groups (Princeton University Press and University of Tokyo Press, Princeton, NJ, 1979).Google Scholar
Soudry, D., Rankin–Selberg Convolutions for SO 2l+1 ×GL n : Local Theory vol. 105, Memoirs of the American Mathematical Society, Volume 500 (American Mathematical Society, Providence, RI, 1993).Google Scholar
Soudry, D., Rankin–Selberg integrals, the descent method, and Langlands functoriality, in ICM, pp. 1311–1325. Madrid, 2006. EMS (Zürich, Switzerland).Google Scholar
Steinberg, R., Générateurs, relations et revêtements de groupes algébriques, in Colloq. Théorie des Groupes Algébriques (Bruxelles, 1962), pp. 113–127 (Librairie Universitaire, Louvain, 1962).Google Scholar
Steinberg, R., Lectures on Chevalley Groups (Yale University, New Haven, CT, 1968). Notes prepared by John Faulkner and Robert Wilson.Google Scholar
Sun, H., Examples of metaplectic tensor products, Preprint, available at http://www.geocities.ws/mathtester/pubs/tensor.pdf (1997), last accessed July 2015.Google Scholar
Sun, H., Remarks on certain metaplectic groups, Canad. Math. Bull. 41(4) (1998), 488–496.CrossRefGoogle Scholar
Szpruch, D., The Langlands–Shahidi Method for the metaplectic group and applications, Thesis, Tel-Aviv University, Israel (2010).Google Scholar
Takeda, S., Metaplectic tensor products for automorphic representations of $\tilde{\text{GL}}(\text{r})$ , Canad. J. Math. (to appear) doi:10.4153/CJM-2014-046-2 Preprint, 2013, arXiv:1303.2785 [math.RT].CrossRefGoogle Scholar
Takeda, S., The twisted symmetric square L-function of GL(r), Duke Math. J. 163(1) (2014), 175–266.Google Scholar
Torasso, P., Méthode des orbites de Kirillov-Duflo et représentations minimales des groupes simples sur un corps local de caractéristique nulle, Duke Math. J. 90(2) (1997), 261–377.CrossRefGoogle Scholar
Vogan, D. A. Jr., Singular unitary representations, in Noncommutative Harmonic Analysis and Lie Groups (Marseille, 1980), Lecture Notes in Mathematics, Volume 880, pp. 506–535 (Springer, Berlin, 1981).Google Scholar
Weil, A., Sur certains groupes d’opérateurs unitaires, Acta Math. 111(1) (1964), 143–211.Google Scholar
Weil, A., Basic Number Theory, Classics in Mathematics (Springer, Berlin, 1995). Reprint of the second (1973 edition).Google Scholar