Article contents
DISMANTLABLE CLASSIFYING SPACE FOR THE FAMILY OF PARABOLIC SUBGROUPS OF A RELATIVELY HYPERBOLIC GROUP
Published online by Cambridge University Press: 11 April 2017
Abstract
Let 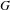 $G$ be a group hyperbolic relative to a finite collection of subgroups
$G$ be a group hyperbolic relative to a finite collection of subgroups 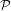 ${\mathcal{P}}$. Let
${\mathcal{P}}$. Let 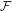 ${\mathcal{F}}$ be the family of subgroups consisting of all the conjugates of subgroups in
${\mathcal{F}}$ be the family of subgroups consisting of all the conjugates of subgroups in 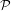 ${\mathcal{P}}$, all their subgroups, and all finite subgroups. Then there is a cocompact model for
${\mathcal{P}}$, all their subgroups, and all finite subgroups. Then there is a cocompact model for 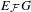 $E_{{\mathcal{F}}}G$. This result was known in the torsion-free case. In the presence of torsion, a new approach was necessary. Our method is to exploit the notion of dismantlability. A number of sample applications are discussed.
$E_{{\mathcal{F}}}G$. This result was known in the torsion-free case. In the presence of torsion, a new approach was necessary. Our method is to exploit the notion of dismantlability. A number of sample applications are discussed.
Keywords
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 18 , Issue 2 , March 2019 , pp. 329 - 345
- Copyright
- © Cambridge University Press 2017
References
- 3
- Cited by


