Article contents
DIFFERENTIAL OPERATORS ON 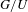 $G/U$ AND THE AFFINE GRASSMANNIAN
$G/U$ AND THE AFFINE GRASSMANNIAN
Published online by Cambridge University Press: 07 April 2014
Abstract
We describe the equivariant cohomology of cofibers of spherical perverse sheaves on the affine Grassmannian of a reductive algebraic group in terms of the geometry of the Langlands dual group. In fact we give two equivalent descriptions: one in terms of 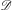 $\mathscr{D}$-modules of the basic affine space, and one in terms of intertwining operators for universal Verma modules. We also construct natural collections of isomorphisms parameterized by the Weyl group in these three contexts, and prove that they are compatible with our isomorphisms. As applications we reprove some results of the first author and of Braverman and Finkelberg.
$\mathscr{D}$-modules of the basic affine space, and one in terms of intertwining operators for universal Verma modules. We also construct natural collections of isomorphisms parameterized by the Weyl group in these three contexts, and prove that they are compatible with our isomorphisms. As applications we reprove some results of the first author and of Braverman and Finkelberg.
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 14 , Issue 3 , July 2015 , pp. 493 - 575
- Copyright
- © Cambridge University Press 2014
References
- 13
- Cited by


