No CrossRef data available.
Article contents
CARTAN SUBALGEBRAS IN DIMENSION DROP ALGEBRAS
Published online by Cambridge University Press: 13 June 2019
Abstract
We completely classify Cartan subalgebras of dimension drop algebras with coprime parameters. More generally, we classify Cartan subalgebras of arbitrary stabilised dimension drop algebras that are non-degenerate in the sense that the dimensions of their fibres in the endpoints are maximal. Conjugacy classes by an automorphism are parametrised by certain congruence classes of matrices over the natural numbers with prescribed row and column sums. In particular, each dimension drop algebra admits only finitely many non-degenerate Cartan subalgebras up to conjugacy. As a consequence of this parametrisation, we can provide examples of subhomogeneous 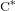 $\text{C}^{\ast }$-algebras with exactly
$\text{C}^{\ast }$-algebras with exactly  $n$ Cartan subalgebras up to conjugacy. Moreover, we show that in many dimension drop algebras two Cartan subalgebras are conjugate if and only if their spectra are homeomorphic.
$n$ Cartan subalgebras up to conjugacy. Moreover, we show that in many dimension drop algebras two Cartan subalgebras are conjugate if and only if their spectra are homeomorphic.
MSC classification
- Type
- Research Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s) 2019



