Research Article
Multipliers for Hardy spaces on locally compact Vilenkin groups
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-301
-
- Article
-
- You have access
- Export citation
On 4-manifolds with universal covering space a compact geometric manifold
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 137-148
-
- Article
-
- You have access
- Export citation
Incompressible surfaces and the topology of 3-dimensional manifolds
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-22
-
- Article
-
- You have access
- Export citation
The structure of exponential Weyl algebras
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 302-310
-
- Article
-
- You have access
- Export citation
Cusps, triangle groups and hyperbolic 3-folds
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 149-182
-
- Article
-
- You have access
- Export citation
The minimal volume of the plane
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 23-40
-
- Article
-
- You have access
- Export citation
On mean curvature flow of spacelike hypersurfaces in asymptotically flat spacetimes
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 41-59
-
- Article
-
- You have access
- Export citation
On Mahler's compound bodies
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 183-215
-
- Article
-
- You have access
- Export citation
A natural representation of partitions as terms of a universal algebra
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 311-324
-
- Article
-
- You have access
- Export citation
On rings all of whose factor rings are integral domains
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 325-333
-
- Article
-
- You have access
- Export citation
Topologically rigid non-Haken 3-manifolds
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 60-71
-
- Article
-
- You have access
- Export citation
On Hausdorff dimension for attractors of iterated function systems
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 216-231
-
- Article
-
- You have access
- Export citation
Tubular sets and multivariate Polya algorithm
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 232-237
-
- Article
-
- You have access
- Export citation
Inhomogeneous minima of a class of ternary quadratic forms
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 334-354
-
- Article
-
- You have access
- Export citation
Hyperbolic manifolds and degenerating handle additions
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 72-89
-
- Article
-
- You have access
- Export citation
Three additive congruences to a large prime modulus
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 355-368
-
- Article
-
- You have access
- Export citation
Pairs of rings with a bijective correspondence between the prime spectra
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 238-245
-
- Article
-
- You have access
- Export citation
Roots of unity and the character variety of a knot complement
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 90-99
-
- Article
-
- You have access
- Export citation
Generation of generators of holomorphic semigroups
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 246-269
-
- Article
-
- You have access
- Export citation
Coincidence and common fixed points of hybrid contractions
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 369-385
-
- Article
-
- You have access
- Export citation



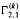 denote the
denote the 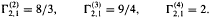
 is already known. For non-zero forms it is proved that
is already known. For non-zero forms it is proved that 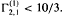 .
.