Research Article
Limit theorems for isotropic random walks on triangle buildings
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 301-334
-
- Article
-
- You have access
- Export citation
Finite graphs of valency 4 and girth 4 admitting half-transitive group actions
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 155-170
-
- Article
-
- You have access
- Export citation
On the class of functions convex in the negative direction of the imaginary axis
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-10
-
- Article
-
- You have access
- Export citation
Average co-ordinate entropy
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 171-186
-
- Article
-
- You have access
- Export citation
Rings in which certain right ideals are direct summands of annihilators
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 335-346
-
- Article
-
- You have access
- Export citation
Matrix-variate Kummer-Beta distribution
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 11-26
-
- Article
-
- You have access
- Export citation
Moment sequences and backward extensions of subnormal weighted shifts
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 27-36
-
- Article
-
- You have access
- Export citation
Strong and full dualisability: three-element unary algebras
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 187-220
-
- Article
-
- You have access
- Export citation
On the notion of residual finiteness for G-spaces
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 347-356
-
- Article
-
- You have access
- Export citation
The number of limit cycles for a class of quintic Hamiltonian systems under quintic perturbations
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 37-54
-
- Article
-
- You have access
- Export citation
The Lindelöf principle and angular derivatives in convex domains of finite type
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 221-250
-
- Article
-
- You have access
- Export citation
Characteristic invatiant of tensor product actions and actions on crossed products
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 357-376
-
- Article
-
- You have access
- Export citation
Strong duality for metacyclic groups
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 377-392
-
- Article
-
- You have access
- Export citation
Metanilpotent varieties of groups
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 55-84
-
- Article
-
- You have access
- Export citation
The Schur and (weak) Dunford-Pettis properties in Banach lattices
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 251-278
-
- Article
-
- You have access
- Export citation
Irreducible subgroups of symplectic groups in characteristic 2
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 85-96
-
- Article
-
- You have access
- Export citation
Analyse conforme sur les algèbres de Jordan
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 279-300
-
- Article
-
- You have access
- Export citation
Bounds for nilpotent-by-finite groups in certain varieties
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 393-404
-
- Article
-
- You have access
- Export citation
Sums of Cantor sets yielding an interval
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 405-418
-
- Article
-
- You have access
- Export citation
Front matter
JAZ volume 73 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation



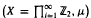 is introduced. This quantity-average co-ordinate or AC entropy-is calculated for product measures and
is introduced. This quantity-average co-ordinate or AC entropy-is calculated for product measures and 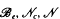 and
and 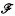 denote respectively the variety of groups of exponent dividing
denote respectively the variety of groups of exponent dividing 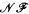 . We show that
. We show that 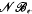 but we characterize the varieties in which that is possible. In this case, there exists a function
but we characterize the varieties in which that is possible. In this case, there exists a function 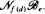 So, when
So, when 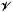 forms a variety if and only if
forms a variety if and only if 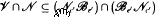 for some integers
for some integers  is an interval if and only if a /(1−2
is an interval if and only if a /(1−2