Research Article
A NOTE ON THE CLOSURE OF CONVOLUTION POWER MIXTURES (RANDOM SUMS) OF EXPONENTIAL DISTRIBUTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2008, pp. 1-7
-
- Article
-
- You have access
- Export citation
A NOTE ON LOCALISED WEIGHTED INEQUALITIES FOR THE EXTENSION OPERATOR
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2008, pp. 289-299
-
- Article
-
- You have access
- Export citation
STRONGLY IRREDUCIBLE IDEALS
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 145-154
-
- Article
-
- You have access
- Export citation
DIFFERENCES OF COMPOSITION OPERATORS BETWEEN WEIGHTED BANACH SPACES OF HOLOMORPHIC FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2008, pp. 9-20
-
- Article
-
- You have access
- Export citation
ENERGY OF GLOBAL FRAMES
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 155-162
-
- Article
-
- You have access
- Export citation
ON η3(aτ)η3(bτ) WITH a+b=8
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2008, pp. 301-313
-
- Article
-
- You have access
- Export citation
A PARABOLIC SINGULAR INTEGRAL OPERATOR WITH ROUGH KERNEL
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 163-179
-
- Article
-
- You have access
- Export citation
THE K-THEORY OF SOME HIGHER RANK EXEL–LACA ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2008, pp. 21-38
-
- Article
-
- You have access
- Export citation
MODULAR DIOPHANTINE INEQUALITIES AND ROTATIONS OF NUMERICAL SEMIGROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2008, pp. 315-328
-
- Article
-
- You have access
- Export citation
CONVOLUTION OPERATORS AND HOMOMORPHISMS OF LOCALLY COMPACT GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2008, pp. 329-344
-
- Article
-
- You have access
- Export citation
CANCELLATIVE AND MALCEV PRESENTATIONS FOR FINITE REES INDEX SUBSEMIGROUPS AND EXTENSIONS
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2008, pp. 39-61
-
- Article
-
- You have access
- Export citation
MIXED NORM ESTIMATES FOR POTENTIAL OPERATORS RELATED TO THE RADON TRANSFORM
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 181-191
-
- Article
-
- You have access
- Export citation
REMARKS ON ℓ1 AND
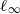 -MAXIMAL REGULARITY FOR POWER-BOUNDED OPERATORS
-MAXIMAL REGULARITY FOR POWER-BOUNDED OPERATORS
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2008, pp. 345-365
-
- Article
-
- You have access
- Export citation
Re-nnd SOLUTIONS OF THE MATRIX EQUATION AXB=C
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2008, pp. 63-72
-
- Article
-
- You have access
- Export citation
THE SPECTRAL TYPE OF SUMS OF OPERATORS ON NON-HILBERTIAN BANACH LATTICES
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 193-198
-
- Article
-
- You have access
- Export citation
INVARIANT SUBSPACES IN THE BIDISC AND WANDERING SUBSPACES
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2008, pp. 367-374
-
- Article
-
- You have access
- Export citation
I0 SETS FOR COMPACT, CONNECTED GROUPS: INTERPOLATION WITH MEASURES THAT ARE NONNEGATIVE OR OF SMALL SUPPORT
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 199-215
-
- Article
-
- You have access
- Export citation
THE COMPLEX INVERSION FORMULA REVISITED
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2008, pp. 73-83
-
- Article
-
- You have access
- Export citation
THE SPECTRA OF THE SPHERICAL AND EUCLIDEAN TRIANGLE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2007, pp. 217-227
-
- Article
-
- You have access
- Export citation
THE SYMMETRIC GROUP REPRESENTATION ON COHOMOLOGY OF THE REGULAR ELEMENTS OF A MAXIMAL TORUS OF THE SPECIAL LINEAR GROUP
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2008, pp. 85-98
-
- Article
-
- You have access
- Export citation



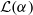 under convolution power mixtures (random summation).
under convolution power mixtures (random summation).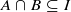 implies that either
implies that either 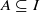 or
or 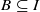 . In this paper we study strongly irreducible ideals in different rings. The relations between strongly irreducible ideals of a ring and strongly irreducible ideals of localizations of the ring are also studied. Furthermore, a topology similar to the Zariski topology related to strongly irreducible ideals is introduced. This topology has the Zariski topology defined by prime ideals as one of its subspace topologies.
. In this paper we study strongly irreducible ideals in different rings. The relations between strongly irreducible ideals of a ring and strongly irreducible ideals of localizations of the ring are also studied. Furthermore, a topology similar to the Zariski topology related to strongly irreducible ideals is introduced. This topology has the Zariski topology defined by prime ideals as one of its subspace topologies.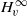 or
or 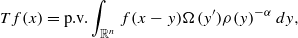
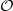 be a higher rank Exel–Laca algebra generated by an alphabet
be a higher rank Exel–Laca algebra generated by an alphabet 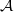 . If
. If 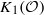 is trivial and
is trivial and  is isomorphic to
is isomorphic to  , let
, let 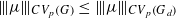 , for
, for 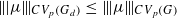 . These inequalities were already known for
. These inequalities were already known for 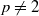 . Finally, for
. Finally, for 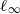 -MAXIMAL REGULARITY FOR POWER-BOUNDED OPERATORS
-MAXIMAL REGULARITY FOR POWER-BOUNDED OPERATORS
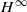 -calculus, and give a complete characterization of this condition in the case of Banach spaces which are
-calculus, and give a complete characterization of this condition in the case of Banach spaces which are 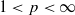 . We show here that this conjecture is false. Indeed for a large class of reflexive spaces, the above property characterizes Hilbert space.
. We show here that this conjecture is false. Indeed for a large class of reflexive spaces, the above property characterizes Hilbert space.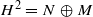 . Using the wandering subspace of
. Using the wandering subspace of