Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-17T17:19:52.004Z Has data issue: false hasContentIssue false
  • English
  • Français

Splitting theorems in abelian-by-hypercyclic groups

Part of: Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  09 April 2009

M. J. Tomkinson
M. J. Tomkinson
Affiliation:
Department of Mathematics University of GlasgowGlasgow G12 8QWScotland
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If 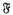is a saturated formation of finite soluble groups and G is a finite group whose 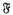-residual A is abelian then it is well known that G splits over A and the complements are conjugate. Hartley and Tomkinson (1975) considered the special case of this result in which 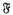is the class of nilpotent groups and obtained similar results for abelian-by-hypercentral groups with rank restrictions on the abelian normal subgroup. Here we consider the super-soluble case, obtaining corresponding results for abelian-by-hypercyclic groups.

MSC classification

Secondary: 20E15: Chains and lattices of subgroups, subnormal subgroups
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 25 , Issue 1 , February 1978 , pp. 71 - 91
Copyright
Copyright © Australian Mathematical Society 1978

References

Baer, R. (1972), “Durch Formationen bestimmte Zerlegungen von Normalteilern endlicher Gruppen”, J. Algebra 20, 38–56.CrossRefGoogle Scholar
Carter, R. and Hawkes, T. (1967), “The F-normalizers of a finite soluble group”, J. Algebra 5, 175–202.CrossRefGoogle Scholar
Fuchs, L. (1973), Infinite Abelian Groups, II, Pure and Applied Mathematics, 36-II (Academic Press, New York and London).Google Scholar
Gardiner, A. D., Hartley, B. and Tomkinson, M. J. (1971), “Saturated formations and Sylow structure in locally finite groups”, J. Algebra 17, 177–211.CrossRefGoogle Scholar
Hall, P. (1958), “Some sufficient conditions for a group to be nilpotent”, Illinois J. Math. 2, 787–801.CrossRefGoogle Scholar
Hartley, B. and Tomkinson, M. J. (1975), “Splitting over nilpotent and hypercentral residuals”, Math. Proc. Cambridge Philos. Soc. 78, 215–226.CrossRefGoogle Scholar
Newell, M. L. (1975), “Some splitting theorems for infinite supersoluble groups”, Math. Z. 144, 265–275.CrossRefGoogle Scholar
Robinson, D. J. S. (1968a), “Residual properties of some classes of infinite soluble groups”, Proc. London Math. Soc. (3) 18, 495–520.CrossRefGoogle Scholar
Robinson, D. J. S. (1968b), “A property of the lower central series of a group”, Math. Z. 107, 225–231.CrossRefGoogle Scholar
Robinson, D. J. S. (1972a), Finiteness Conditions and Generalized Soluble Groups, Part 1, Ergebnisse der Mathematik und ihrer Grenzgebiete, 62 (Springer-Verlag, Berlin, Heidelberg and New York).Google Scholar
Robinson, D. J. S. (1972b), Finiteness Conditions and Generalized Soluble Groups, Part 2, Ergebnisse der Mathematik und ihrer Grenzgebiete, 63 (Springer-Verlag, Berlin, Heidelberg and New York).Google Scholar
Robinson, D. J. S. (1976), “The vanishing of certain homology and cohomology groups”, J. Pure Appl. Algebra 7, 145–167.CrossRefGoogle Scholar
Wehrfritz, B. A. F. (1973), Infinite Linear Groups. An Account of the Group-theoretic Properties of Infinite Groups of Matrices, Ergebnisse der Mathematik und ihrer Grenzgebiete, 76 (Springer-Verlag, Berlin, Heidelberg and New York).Google Scholar