Article contents
SHARP CONSTANTS FOR MULTIVARIATE HAUSDORFF 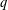 $q$-INEQUALITIES
$q$-INEQUALITIES
Published online by Cambridge University Press: 07 June 2018
Abstract
In this paper, we focus on the multivariate Hausdorff operator of the form 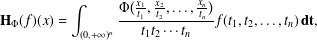 $$\begin{eqnarray}\mathbf{H}_{\unicode[STIX]{x1D6F7}}(f)(x)=\int _{(0,+\infty )^{n}}{\displaystyle \frac{\unicode[STIX]{x1D6F7}\big(\frac{x_{1}}{t_{1}},\frac{x_{2}}{t_{2}},\ldots ,\frac{x_{n}}{t_{n}}\big)}{t_{1}t_{2}\cdots t_{n}}}f(t_{1},t_{2},\ldots ,t_{n})\,\mathbf{dt},\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{H}_{\unicode[STIX]{x1D6F7}}(f)(x)=\int _{(0,+\infty )^{n}}{\displaystyle \frac{\unicode[STIX]{x1D6F7}\big(\frac{x_{1}}{t_{1}},\frac{x_{2}}{t_{2}},\ldots ,\frac{x_{n}}{t_{n}}\big)}{t_{1}t_{2}\cdots t_{n}}}f(t_{1},t_{2},\ldots ,t_{n})\,\mathbf{dt},\end{eqnarray}$$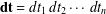 $\mathbf{dt}=dt_{1}\,dt_{2}\cdots \,dt_{n}$ or
$\mathbf{dt}=dt_{1}\,dt_{2}\cdots \,dt_{n}$ or 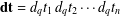 $\mathbf{dt}=d_{q}t_{1}\,d_{q}t_{2}\cdots d_{q}t_{n}$ is the discrete measure in
$\mathbf{dt}=d_{q}t_{1}\,d_{q}t_{2}\cdots d_{q}t_{n}$ is the discrete measure in 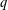 $q$-analysis. The sharp bounds for the multivariate Hausdorff operator on spaces
$q$-analysis. The sharp bounds for the multivariate Hausdorff operator on spaces 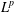 $L^{p}$ with power weights are calculated, where
$L^{p}$ with power weights are calculated, where  $p\in \mathbb{R}\backslash \{0\}$.
$p\in \mathbb{R}\backslash \{0\}$.
- Type
- Research Article
- Information
- Copyright
- © 2018 Australian Mathematical Publishing Association Inc.
Footnotes
The research was supported by National Natural Science Foundation of China (Grant Nos. 11471288, 11601456).
References
- 8
- Cited by


