Article contents
SEMISIMPLICITY OF HECKE AND (WALLED) BRAUER ALGEBRAS
Published online by Cambridge University Press: 25 October 2016
Abstract
We show how to use Jantzen’s sum formula for Weyl modules to prove semisimplicity criteria for endomorphism algebras of  $\mathbf{U}_{q}$-tilting modules (for any field
$\mathbf{U}_{q}$-tilting modules (for any field 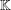 $\mathbb{K}$ and any parameter
$\mathbb{K}$ and any parameter  $q\in \mathbb{K}-\{0,-1\}$). As an application, we recover the semisimplicity criteria for the Hecke algebras of types
$q\in \mathbb{K}-\{0,-1\}$). As an application, we recover the semisimplicity criteria for the Hecke algebras of types 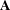 $\mathbf{A}$ and
$\mathbf{A}$ and 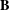 $\mathbf{B}$, the walled Brauer algebras and the Brauer algebras from our more general approach.
$\mathbf{B}$, the walled Brauer algebras and the Brauer algebras from our more general approach.
Keywords
- Type
- Research Article
- Information
- Copyright
- © 2016 Australian Mathematical Publishing Association Inc.
Footnotes
Elements of the text in the article appear in colour online available at 10.1017/S1446788716000392.
H.H.A. was supported by the Center of Excellence grant ‘Centre for Quantum Geometry of Moduli Spaces (QGM)’ from the Danish National Research Foundation (DNRF), C.S. by a Hirzebruch professorship of the Max-Planck-Gesellschaft and D.T. by a research funding of the Deutsche Forschungsgemeinschaft (DFG) during this work.
References
- 10
- Cited by


