Published online by Cambridge University Press: 17 June 2013
Let 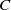 $C$ be a curve in a closed orientable surface
$C$ be a curve in a closed orientable surface 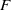 $F$ of genus
$F$ of genus 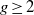 $g\geq 2$ that separates
$g\geq 2$ that separates  $F$ into subsurfaces
$F$ into subsurfaces 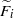 $\widetilde {{F}_{i} } $ of genera
$\widetilde {{F}_{i} } $ of genera 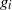 ${g}_{i} $, for
${g}_{i} $, for 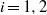 $i= 1, 2$. We study the set of roots in
$i= 1, 2$. We study the set of roots in 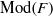 $\mathrm{Mod} (F)$ of the Dehn twist
$\mathrm{Mod} (F)$ of the Dehn twist 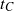 ${t}_{C} $ about
${t}_{C} $ about  $C$. All roots arise from pairs of
$C$. All roots arise from pairs of  ${C}_{{n}_{i} } $-actions on the
${C}_{{n}_{i} } $-actions on the  $\widetilde {{F}_{i} } $, where
$\widetilde {{F}_{i} } $, where 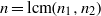 $n= \mathrm{lcm} ({n}_{1} , {n}_{2} )$ is the degree of the root, that satisfy a certain compatibility condition. The
$n= \mathrm{lcm} ({n}_{1} , {n}_{2} )$ is the degree of the root, that satisfy a certain compatibility condition. The 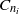 ${C}_{{n}_{i} } $-actions are of a kind that we call nestled actions, and we classify them using tuples that we call data sets. The compatibility condition can be expressed by a simple formula, allowing a classification of all roots of
${C}_{{n}_{i} } $-actions are of a kind that we call nestled actions, and we classify them using tuples that we call data sets. The compatibility condition can be expressed by a simple formula, allowing a classification of all roots of 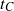 ${t}_{C} $ by compatible pairs of data sets. We use these data set pairs to classify all roots for
${t}_{C} $ by compatible pairs of data sets. We use these data set pairs to classify all roots for 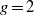 $g= 2$ and
$g= 2$ and 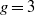 $g= 3$. We show that there is always a root of degree at least
$g= 3$. We show that there is always a root of degree at least 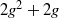 $2{g}^{2} + 2g$, while
$2{g}^{2} + 2g$, while 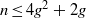 $n\leq 4{g}^{2} + 2g$. We also give some additional applications.
$n\leq 4{g}^{2} + 2g$. We also give some additional applications.