Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T01:51:56.160Z Has data issue: false hasContentIssue false
  • English
  • Français

The ~ -representations of symmetric homogeneous algebras

Part of: Locally compact groups and their algebras Abstract harmonic analysis

Published online by Cambridge University Press:  09 April 2009

J. A. Ward
J. A. Ward
Affiliation:
School of Mathematical and Physical Sciences, Murdoch University, Murdoch, Western Australia 6155, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In 1947 I. E. Segal proved that to each non-degenerate ~ -representation R of L1 (= L1 (G) for a compact group G) with representation space , there corresponds a continuous unitary representation W of G, also with representation space , which satisfies

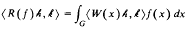
for each fL1 and hk. This was extended to Lp,1p < , in 1970 by E. Hewitt and K. A. Ross. We now generalize this result to any symmetric homogeneous convolution Banach alebra of pseudomeasures on G. Further we prove that the correspondence preserves irreduibility.

MSC classification

Secondary: 22D20: Representations of group algebras 43A65: Representations of groups, semigroups, etc.
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 40 , Issue 2 , April 1986 , pp. 267 - 275
Copyright
Copyright Australian Mathematical Society 1986

References

1Edwards, R. E., Functional analysis, theory and applications (Holt, Rinehart and Winston, New York, 1965).Google Scholar
2Hewitt, E. and Ross, K. A., Abstract harmonic analysis, Vols. 1 and 2 (Springer-Verlag, Berlin, 1963 and 1970).Google Scholar
3Naimark, M. A., Normed rings (Noordhoff, Groningen, 1959).Google Scholar
4Segal, I. E., The group algebra of a locally compact group, Trans. Amer. Math. Soc. 61 (1947), 69105.Google Scholar
5Ward, J. A., Characterization of homogeneous spaces and their norms, Pacific J. Math. 114 (1984), 481495.Google Scholar
6Ward, J. A., Closed ideals of homogeneous algebras, Monatsh. Math. 96 (1983), 317324.Google Scholar