No CrossRef data available.
Article contents
Relations on topological spaces: Urysohn's lemma
Published online by Cambridge University Press: 09 April 2009
Extract
Let X be a topological space equipped with a binary relation R; that is, R is a subset of the Cartesian square X×X. Following Wallace [5], we write 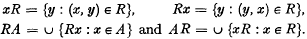 Deviating from [7], we shall follow Wallace [4] to call the relation R continuous if RA*⊂(RA)* for each A⊂X, where * designates the topological closure. Borrowing the language from the Ordered System, though our relation R need not be any kind of order relation, we say that a subset S of X is R-decreasing (R-increasing) if RS ⊂ S(SR ⊂ S), and that S is Rmonotone if S is either R-decreasing or R-increasing. Two R-monotone subsets are of the same type if they are either both R-decresaing or both Rincreasing.
Deviating from [7], we shall follow Wallace [4] to call the relation R continuous if RA*⊂(RA)* for each A⊂X, where * designates the topological closure. Borrowing the language from the Ordered System, though our relation R need not be any kind of order relation, we say that a subset S of X is R-decreasing (R-increasing) if RS ⊂ S(SR ⊂ S), and that S is Rmonotone if S is either R-decreasing or R-increasing. Two R-monotone subsets are of the same type if they are either both R-decresaing or both Rincreasing.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1968


