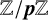1 Introduction
A fundamental result in the theory of elliptic curves is the Mordell–Weil theorem. It states that given an elliptic curve E defined over a number field F, its F-rational points form a finitely generated abelian group, that is,
where r is a nonnegative integer called the rank and
![]() $E(F)_{\operatorname {\mathrm {tors}}}$
is a finite group, called the torsion subgroup. Over
$E(F)_{\operatorname {\mathrm {tors}}}$
is a finite group, called the torsion subgroup. Over
![]() ${\mathbb Q}$
, the possible structures of
${\mathbb Q}$
, the possible structures of
![]() $E({\mathbb Q})_{\operatorname {\mathrm {tors}}}$
are known by the work of Mazur (see [Reference MazurMaz77, Reference MazurMaz78]). These techniques have been extended by Kamienny, Kenku, and Momose (see for example [Reference Kenku and MomoseKM88, Reference KamiennyKam92]) to provide the complete classification of torsion subgroups for quadratic fields. More recently, in a series of works by several authors, the classification of torsion subgroups for cubic fields has been completed (see, for example, [Reference Bruin and NajmanBN16, Reference Derickx, Etropolski, van Hoeij, Morrow and Zureick-BrownDEvH+21, Reference Derickx and NajmanDN19, Reference Jeon, Kim and LeeJKL11, Reference Jeon, Kim and SchweizerJKS04, Reference NajmanNaj16, Reference WangWan15]). In [Reference MerelMer96], Merel proved that for elliptic curves over any number field, the bound of the order of the torsion subgroup depends only on the degree of the number field. Despite remarkable advances made toward understanding the torsion subgroup, the rank remains mysterious and, to date, there is no known algorithm to compute it. Almost always, obtaining information about the rank of the elliptic curve involves studying the Selmer group.
$E({\mathbb Q})_{\operatorname {\mathrm {tors}}}$
are known by the work of Mazur (see [Reference MazurMaz77, Reference MazurMaz78]). These techniques have been extended by Kamienny, Kenku, and Momose (see for example [Reference Kenku and MomoseKM88, Reference KamiennyKam92]) to provide the complete classification of torsion subgroups for quadratic fields. More recently, in a series of works by several authors, the classification of torsion subgroups for cubic fields has been completed (see, for example, [Reference Bruin and NajmanBN16, Reference Derickx, Etropolski, van Hoeij, Morrow and Zureick-BrownDEvH+21, Reference Derickx and NajmanDN19, Reference Jeon, Kim and LeeJKL11, Reference Jeon, Kim and SchweizerJKS04, Reference NajmanNaj16, Reference WangWan15]). In [Reference MerelMer96], Merel proved that for elliptic curves over any number field, the bound of the order of the torsion subgroup depends only on the degree of the number field. Despite remarkable advances made toward understanding the torsion subgroup, the rank remains mysterious and, to date, there is no known algorithm to compute it. Almost always, obtaining information about the rank of the elliptic curve involves studying the Selmer group.
Let p be a prime number. In [Reference MazurMaz72], Mazur initiated the study of p-primary Selmer groups of elliptic curves in
![]() ${\mathbb Z}_p$
-extensions. Since then, Iwasawa theory of elliptic curves has been successfully used by many authors to study rank growth in towers of number fields. However, the scope of this paper is different. We use results from Iwasawa theory of Selmer groups of elliptic curves to obtain results on rank growth in cyclic degree-p extensions. Let
${\mathbb Z}_p$
-extensions. Since then, Iwasawa theory of elliptic curves has been successfully used by many authors to study rank growth in towers of number fields. However, the scope of this paper is different. We use results from Iwasawa theory of Selmer groups of elliptic curves to obtain results on rank growth in cyclic degree-p extensions. Let
![]() $L/{\mathbb Q}$
be a finite extension and E an elliptic curve over
$L/{\mathbb Q}$
be a finite extension and E an elliptic curve over
![]() ${\mathbb Q}$
. Mazur and Rubin [Reference Mazur, Rubin and LarsenMRL18] define E to be diophantine-stable in L if
${\mathbb Q}$
. Mazur and Rubin [Reference Mazur, Rubin and LarsenMRL18] define E to be diophantine-stable in L if
![]() $E(L)=E({\mathbb Q})$
. This property is of significant importance and has applications to Hilbert’s
$E(L)=E({\mathbb Q})$
. This property is of significant importance and has applications to Hilbert’s
![]() $10^{\text {th}}$
problem for number fields. In this paper, we answer the following two questions about growth of Selmer groups in cyclic degree-p extensions.
$10^{\text {th}}$
problem for number fields. In this paper, we answer the following two questions about growth of Selmer groups in cyclic degree-p extensions.
-
(1) Given an elliptic curve
 $E_{/{\mathbb Q}}$
with trivial p-primary Selmer group, for what proportion of degree-p cyclic extensions does the p-primary Selmer group remain trivial upon base-change?
$E_{/{\mathbb Q}}$
with trivial p-primary Selmer group, for what proportion of degree-p cyclic extensions does the p-primary Selmer group remain trivial upon base-change? -
(2) Given a prime
 $p\neq 2,3$
, varying over all elliptic curves defined over
$p\neq 2,3$
, varying over all elliptic curves defined over
 ${\mathbb Q}$
, for what proportion of elliptic curves does there exist at least one
${\mathbb Q}$
, for what proportion of elliptic curves does there exist at least one
 ${\mathbb Z}/p{\mathbb Z}$
-extension where the p-primary Selmer group remains trivial upon base-change?
${\mathbb Z}/p{\mathbb Z}$
-extension where the p-primary Selmer group remains trivial upon base-change?
The proportion of elliptic curves is computed with respect to height (see Equation (3-3)). Our results are proven for elliptic curves
![]() $E_{/{\mathbb Q}}$
with Mordell–Weil rank
$E_{/{\mathbb Q}}$
with Mordell–Weil rank
![]() $0$
. Using standard arguments from Iwasawa theory, one can show that the p-primary Selmer group has rank
$0$
. Using standard arguments from Iwasawa theory, one can show that the p-primary Selmer group has rank
![]() $0$
over the cyclotomic
$0$
over the cyclotomic
![]() ${\mathbb Z}_p$
-extension of a number field L (in particular, over L itself) if and only if the associated
${\mathbb Z}_p$
-extension of a number field L (in particular, over L itself) if and only if the associated
![]() $\mu $
-invariant and
$\mu $
-invariant and
![]() $\lambda $
-invariant are trivial (see for example [Reference Kundu and RayKR21a, Corollary 3.6]). Controlling the
$\lambda $
-invariant are trivial (see for example [Reference Kundu and RayKR21a, Corollary 3.6]). Controlling the
![]() $\mu $
-invariant is relatively easy and it is known to behave well in p-extensions (see Theorem 2.3). So the key idea involves showing how often the
$\mu $
-invariant is relatively easy and it is known to behave well in p-extensions (see Theorem 2.3). So the key idea involves showing how often the
![]() $\lambda $
-invariant remains trivial upon base-change to
$\lambda $
-invariant remains trivial upon base-change to
![]() $L/{\mathbb Q}$
. Given
$L/{\mathbb Q}$
. Given
![]() $n\geq 0$
, let
$n\geq 0$
, let
![]() $L_n$
denote the cyclotomic
$L_n$
denote the cyclotomic
![]() ${\mathbb Z}/p^n{\mathbb Z}$
extension of L. This is the unique
${\mathbb Z}/p^n{\mathbb Z}$
extension of L. This is the unique
![]() ${\mathbb Z}/p^n{\mathbb Z}$
-extension of L contained inside
${\mathbb Z}/p^n{\mathbb Z}$
-extension of L contained inside
![]() $L(\mu _{p^{\infty }})$
. We note that we have at this point in our notation suppressed the dependence on the prime p. Since
$L(\mu _{p^{\infty }})$
. We note that we have at this point in our notation suppressed the dependence on the prime p. Since
![]() $\lambda _p(E/L)\geq \operatorname {\mathrm {rank}}_{{\mathbb Z}}(E(L_n))$
(see Lemma 2.2), proving triviality of the
$\lambda _p(E/L)\geq \operatorname {\mathrm {rank}}_{{\mathbb Z}}(E(L_n))$
(see Lemma 2.2), proving triviality of the
![]() $\lambda $
-invariant upon base-change implies the rank does not change in L. In fact, we prove a stronger result, and show that the rank does not in fact increase in
$\lambda $
-invariant upon base-change implies the rank does not change in L. In fact, we prove a stronger result, and show that the rank does not in fact increase in
![]() $L_n$
for all
$L_n$
for all
![]() $n\geq 0$
. To answer the first question, we prove the following result.
$n\geq 0$
. To answer the first question, we prove the following result.
Theorem A. Let
![]() $E_{/{\mathbb Q}}$
be a non-CM (complex multiplication) elliptic curve and p be a fixed prime number
$E_{/{\mathbb Q}}$
be a non-CM (complex multiplication) elliptic curve and p be a fixed prime number
![]() $\geq 5$
such that the residual representation at p is surjective. Further suppose that
$\geq 5$
such that the residual representation at p is surjective. Further suppose that
![]() $\mu _p(E/{\mathbb Q}) = \lambda _p(E/{\mathbb Q}) =0$
. Then, there are infinitely many
$\mu _p(E/{\mathbb Q}) = \lambda _p(E/{\mathbb Q}) =0$
. Then, there are infinitely many
![]() ${\mathbb Z}/p{\mathbb Z}$
-extensions of
${\mathbb Z}/p{\mathbb Z}$
-extensions of
![]() ${\mathbb Q}$
in which the
${\mathbb Q}$
in which the
![]() $\lambda $
-invariant does not increase. In particular, in infinitely many cyclic degree-p number fields
$\lambda $
-invariant does not increase. In particular, in infinitely many cyclic degree-p number fields
![]() $L/{\mathbb Q}$
, the rank does not grow in
$L/{\mathbb Q}$
, the rank does not grow in
![]() $L_n$
for all
$L_n$
for all
![]() $n\geq 0$
, that is,
$n\geq 0$
, that is,
In the case that
![]() $E_{/{\mathbb Q}}$
is a CM elliptic curve, we can prove a similar result under an additional independence hypothesis which we make precise in Hypothesis 3.10.
$E_{/{\mathbb Q}}$
is a CM elliptic curve, we can prove a similar result under an additional independence hypothesis which we make precise in Hypothesis 3.10.
The condition
![]() $\lambda _p(E/{\mathbb Q})=0$
can only be satisfied for elliptic curves
$\lambda _p(E/{\mathbb Q})=0$
can only be satisfied for elliptic curves
![]() $E_{/{\mathbb Q}}$
of Mordell–Weil rank
$E_{/{\mathbb Q}}$
of Mordell–Weil rank
![]() $0$
, and thus the above result shows that the rank remains
$0$
, and thus the above result shows that the rank remains
![]() $0$
in the fields
$0$
in the fields
![]() $L_n$
.
$L_n$
.
Even though our proof suggests that the
![]() $\lambda $
-invariant does not jump in many
$\lambda $
-invariant does not jump in many
![]() ${\mathbb Z}/p{\mathbb Z}$
-extensions, we are unable to show that this is true for a positive proportion of
${\mathbb Z}/p{\mathbb Z}$
-extensions, we are unable to show that this is true for a positive proportion of
![]() ${\mathbb Z}/p{\mathbb Z}$
-extensions. It is known by the work of Greenberg [Reference Greenberg and ViolaGre99, Theorem 5.1] that given a rank 0 elliptic curve E over
${\mathbb Z}/p{\mathbb Z}$
-extensions. It is known by the work of Greenberg [Reference Greenberg and ViolaGre99, Theorem 5.1] that given a rank 0 elliptic curve E over
![]() ${\mathbb Q}$
, for density one good ordinary primes,
${\mathbb Q}$
, for density one good ordinary primes,
![]() $\mu _p(E/{\mathbb Q}) =\lambda _p(E/{\mathbb Q})=0$
.
$\mu _p(E/{\mathbb Q}) =\lambda _p(E/{\mathbb Q})=0$
.
In a recent paper (see [Reference González-Jiménez and NajmanGJN20]), González-Jiménez and Najman investigated the question of when the torsion group does not grow upon base-change (see Theorem 3.12 for the precise statement). This, when combined with the above theorem, allows us to comment on when the Mordell–Weil group does not grow in
![]() ${\mathbb Z}/p{\mathbb Z}$
-extensions. More precisely, we have the following corollary.
${\mathbb Z}/p{\mathbb Z}$
-extensions. More precisely, we have the following corollary.
Corollary A. Given a non-CM elliptic curve
![]() $E_{/{\mathbb Q}}$
and a prime
$E_{/{\mathbb Q}}$
and a prime
![]() $p>7$
such that the residual representation at p is surjective and
$p>7$
such that the residual representation at p is surjective and
![]() $\mu _p(E/{\mathbb Q}) = \lambda _p(E/{\mathbb Q}) =0$
, there are infinitely many
$\mu _p(E/{\mathbb Q}) = \lambda _p(E/{\mathbb Q}) =0$
, there are infinitely many
![]() ${\mathbb Z}/p{\mathbb Z}$
-extensions
${\mathbb Z}/p{\mathbb Z}$
-extensions
![]() $L/{\mathbb Q}$
such that
$L/{\mathbb Q}$
such that
The same assertion holds for elliptic curves with CM provided Hypothesis 3.10 holds.
A natural extension of the previous question is the following: when does the p-primary Selmer group grow upon base-change? We address this question in Section 4. First, we prove a result regarding the growth of the p-primary Selmer group of an elliptic curve
![]() $E_{/{\mathbb Q}}$
upon base-change of a
$E_{/{\mathbb Q}}$
upon base-change of a
![]() ${\mathbb Z}/p{\mathbb Z}$
-extension (see Proposition 4.1). This result gives a criterion for either the rank to jump or the order of the Shafarevich–Tate group to increase upon base-change. It applies to all primes
${\mathbb Z}/p{\mathbb Z}$
-extension (see Proposition 4.1). This result gives a criterion for either the rank to jump or the order of the Shafarevich–Tate group to increase upon base-change. It applies to all primes
![]() $p\geq 5$
and the method relies on exploiting the relationship between Iwasawa invariants and the Euler characteristic. It is motivated by ideas from [Reference Ray and SujathaRS19, Reference Ray and SujathaRS20], as well as the use of Kida’s formula (Theorem 2.3). This criterion is then used to show that the Selmer group becomes nonzero in a large family of
$p\geq 5$
and the method relies on exploiting the relationship between Iwasawa invariants and the Euler characteristic. It is motivated by ideas from [Reference Ray and SujathaRS19, Reference Ray and SujathaRS20], as well as the use of Kida’s formula (Theorem 2.3). This criterion is then used to show that the Selmer group becomes nonzero in a large family of
![]() ${\mathbb Z}/p{\mathbb Z}$
-extensions. Given an elliptic curve
${\mathbb Z}/p{\mathbb Z}$
-extensions. Given an elliptic curve
![]() $E_{/{\mathbb Q}}$
and a prime p, we set
$E_{/{\mathbb Q}}$
and a prime p, we set
![]() $E[p]$
to denote the p-torsion subgroup of
$E[p]$
to denote the p-torsion subgroup of
![]() $E(\bar {{\mathbb Q}})$
. The residual representation at p refers to the Galois representation
$E(\bar {{\mathbb Q}})$
. The residual representation at p refers to the Galois representation
on
![]() $E[p]$
. More precisely, we can prove the following result.
$E[p]$
. More precisely, we can prove the following result.
Theorem B. Let
![]() $p\geq 5$
be a fixed prime and
$p\geq 5$
be a fixed prime and
![]() $E_{/{\mathbb Q}}$
be an elliptic curve with good ordinary reduction at p. Suppose that the image of the residual representation is surjective, the p-primary Selmer group over
$E_{/{\mathbb Q}}$
be an elliptic curve with good ordinary reduction at p. Suppose that the image of the residual representation is surjective, the p-primary Selmer group over
![]() ${\mathbb Q}$
is trivial, and
${\mathbb Q}$
is trivial, and
![]() $\mu _p(E/{\mathbb Q})=\lambda _p(E/{\mathbb Q})=0$
. Then, there is a set of primes of the form
$\mu _p(E/{\mathbb Q})=\lambda _p(E/{\mathbb Q})=0$
. Then, there is a set of primes of the form
![]() $q\equiv 1\ \pmod {\,p}$
with density at least
$q\equiv 1\ \pmod {\,p}$
with density at least
![]() ${p}/{(p-1)^2(p+1)}$
such that the p-primary Selmer group becomes nontrivial in the unique
${p}/{(p-1)^2(p+1)}$
such that the p-primary Selmer group becomes nontrivial in the unique
![]() ${\mathbb Z}/p{\mathbb Z}$
-extension contained in
${\mathbb Z}/p{\mathbb Z}$
-extension contained in
![]() ${\mathbb Q}(\mu _q)$
.
${\mathbb Q}(\mu _q)$
.
However, we remark that this method is unable to distinguish between jumps in rank and jumps in the order of the Shafarevich–Tate group. These methods are currently being refined by the third named author, and in a subsequent paper, will be applied to a large number of problems in Diophantine stability and arithmetic statistics.
In response to the second question, we show the following.
Theorem C. Suppose that the Shafarevich–Tate group is finite for all rank 0 elliptic curves defined over
![]() ${\mathbb Q}$
and Hypothesis 3.19 holds. For a positive proportion of rank 0 elliptic curves defined over
${\mathbb Q}$
and Hypothesis 3.19 holds. For a positive proportion of rank 0 elliptic curves defined over
![]() ${\mathbb Q}$
, there is at least one
${\mathbb Q}$
, there is at least one
![]() ${\mathbb Z}/p{\mathbb Z}$
-extension over
${\mathbb Z}/p{\mathbb Z}$
-extension over
![]() ${\mathbb Q}$
disjoint from the cyclotomic
${\mathbb Q}$
disjoint from the cyclotomic
![]() ${\mathbb Z}_p$
-extension,
${\mathbb Z}_p$
-extension,
![]() ${\mathbb Q}_{\operatorname {\mathrm {cyc}}}/{\mathbb Q}$
, with trivial p-primary Selmer group upon base-change.
${\mathbb Q}_{\operatorname {\mathrm {cyc}}}/{\mathbb Q}$
, with trivial p-primary Selmer group upon base-change.
Hypothesis 3.19 is the assumption that the proportion of rank 0 elliptic curves (ordered by height) with a fixed reduction type at a prime q is the same as the proportion of all elliptic curves (ordered by height) with the same property. In other words, the reduction type at q is independent of the rank of the elliptic curve.
We remark that the main reason for us to restrict the study to elliptic curves at primes of good ordinary reduction is to ensure that we can use results on
![]() $\lambda $
-invariants of elliptic curves from [Reference Hachimori and MatsunoHM99]. There are recent results which extend the aforementioned theorem to the nonordinary case. It seems reasonable to expect that our results should extend to the supersingular case using the work of Hatley and Lei in [Reference Hatley and LeiHL19, Theorem 6.7].
$\lambda $
-invariants of elliptic curves from [Reference Hachimori and MatsunoHM99]. There are recent results which extend the aforementioned theorem to the nonordinary case. It seems reasonable to expect that our results should extend to the supersingular case using the work of Hatley and Lei in [Reference Hatley and LeiHL19, Theorem 6.7].
In [Reference ČesnavičiusČes17], Česnavičius showed that the p-Selmer group of elliptic curves over a number field becomes arbitrarily large when varying over
![]() ${\mathbb Z}/p{\mathbb Z}$
-extensions. This result is not surprising, as it is widely believed that the growth of ideal class groups and Selmer groups of elliptic curves are often analogous. The unboundedness of the
${\mathbb Z}/p{\mathbb Z}$
-extensions. This result is not surprising, as it is widely believed that the growth of ideal class groups and Selmer groups of elliptic curves are often analogous. The unboundedness of the
![]() $2$
-part of the ideal class group in quadratic extensions goes back to Gauss; for its generalization to an odd prime, see [Reference Borel, Chowla, Herz, Iwasawa and SerreBCH+66, VII-12, Theorem 4]. The rank boundedness conjecture for elliptic curves asks whether there is an upper bound for the Mordell–Weil rank of elliptic curves over number fields. This question is widely open and experts are unable to come to a consensus on what to expect; see [Reference Park, Poonen, Voight and WoodPPVW19, Section 3] for a historical survey. Those in favor of unboundedness argue that this phenomenon provably occurs in other global fields, and that the proven lower bound for this upper bound increases every few years. For instance, N. Elkies discovered an elliptic curve over
$2$
-part of the ideal class group in quadratic extensions goes back to Gauss; for its generalization to an odd prime, see [Reference Borel, Chowla, Herz, Iwasawa and SerreBCH+66, VII-12, Theorem 4]. The rank boundedness conjecture for elliptic curves asks whether there is an upper bound for the Mordell–Weil rank of elliptic curves over number fields. This question is widely open and experts are unable to come to a consensus on what to expect; see [Reference Park, Poonen, Voight and WoodPPVW19, Section 3] for a historical survey. Those in favor of unboundedness argue that this phenomenon provably occurs in other global fields, and that the proven lower bound for this upper bound increases every few years. For instance, N. Elkies discovered an elliptic curve over
![]() ${\mathbb Q}$
with Mordell–Weil rank at least 28. However, a recent series of papers by B. Poonen et al. provides a justified heuristic inspired by ideas from arithmetic statistics which suggests otherwise (see for example [Reference PoonenPoo18]).
${\mathbb Q}$
with Mordell–Weil rank at least 28. However, a recent series of papers by B. Poonen et al. provides a justified heuristic inspired by ideas from arithmetic statistics which suggests otherwise (see for example [Reference PoonenPoo18]).
The interplay between the rank, Selmer group, and the Shafarevich–Tate group raises the question of producing elliptic curves with ‘large Shafarevich–Tate groups’. More precisely, given a number field F, a prime p, and a positive integer n, does there exist an elliptic curve
![]() $E_{/F}$
whose Shafarevich–Tate group contains at least n elements of order p? A dual question one can ask is the following: given
$E_{/F}$
whose Shafarevich–Tate group contains at least n elements of order p? A dual question one can ask is the following: given
![]() $E_{/{\mathbb Q}}$
, a positive integer n, and a prime p, does there exist a number field
$E_{/{\mathbb Q}}$
, a positive integer n, and a prime p, does there exist a number field
![]() $F/{\mathbb Q}$
(with additional properties) such that the Shafarevich–Tate group, denoted by
$F/{\mathbb Q}$
(with additional properties) such that the Shafarevich–Tate group, denoted by
![]() , contains at least n elements of order p?
, contains at least n elements of order p?
In the final section, we study growth questions for Shafarevich–Tate groups. When
![]() $p=2$
, K. Matsuno showed that the 2-rank of the Shafarevich–Tate group becomes arbitrarily large in quadratic extensions of number fields (see [Reference MatsunoMat09]). In Theorem 5.7, we prove an effective version of this theorem for elliptic curves without any exceptional primes. In particular, given
$p=2$
, K. Matsuno showed that the 2-rank of the Shafarevich–Tate group becomes arbitrarily large in quadratic extensions of number fields (see [Reference MatsunoMat09]). In Theorem 5.7, we prove an effective version of this theorem for elliptic curves without any exceptional primes. In particular, given
![]() $n>0$
, we find an upper bound on the minimal conductor of the quadratic extension (say K) such that
$n>0$
, we find an upper bound on the minimal conductor of the quadratic extension (say K) such that
![]() . Recently, it has been shown in [Reference Morgan and PatersonMP22] that there are infinitely many elliptic curves with large
. Recently, it has been shown in [Reference Morgan and PatersonMP22] that there are infinitely many elliptic curves with large
![]() . When
. When
![]() $p\neq 2$
, P. Clark and S. Sharif showed that varying over all degree-p extensions of
$p\neq 2$
, P. Clark and S. Sharif showed that varying over all degree-p extensions of
![]() ${\mathbb Q}$
, not necessarily Galois, the p-rank of the Shafarevich–Tate group can become arbitrarily large; see [Reference Clark and SharifCS10]. They further raised a question as to whether this result is the best possible. In Section 5.2, we show that if a conjecture of C. David, J. Fearnley, and H. Kisilevsky is true (see Section 2.2 for the precise statement), then the result of Clark and Sharif can be improved. In particular, instead of varying over all degree-p extensions, it suffices to vary over all
${\mathbb Q}$
, not necessarily Galois, the p-rank of the Shafarevich–Tate group can become arbitrarily large; see [Reference Clark and SharifCS10]. They further raised a question as to whether this result is the best possible. In Section 5.2, we show that if a conjecture of C. David, J. Fearnley, and H. Kisilevsky is true (see Section 2.2 for the precise statement), then the result of Clark and Sharif can be improved. In particular, instead of varying over all degree-p extensions, it suffices to vary over all
![]() ${\mathbb Z}/p{\mathbb Z}$
-extensions of
${\mathbb Z}/p{\mathbb Z}$
-extensions of
![]() ${\mathbb Q}$
.
${\mathbb Q}$
.
Organization: Including this Introduction, the article has six sections. Section 2 is preliminary in nature; after introducing the main objects of interest, we record relevant results from Iwasawa theory. We also mention some conjectures and heuristics on rank growth of elliptic curves in Galois extensions. In Section 3, we use techniques from Iwasawa theory to prove results on rank jump of elliptic curves in cyclic degree-p extensions. In Section 4, we study arithmetic statistics related questions pertaining to the growth of the p-primary Selmer groups in
![]() ${\mathbb Z}/p{\mathbb Z}$
-extensions. In Section 5, we study the growth of the p-rank of the Shafarevich–Tate group in cyclic degree-p extensions. One of our results on rank growth requires a mild hypothesis; we provide computational evidence for the same. The table is included in Section 6.
${\mathbb Z}/p{\mathbb Z}$
-extensions. In Section 5, we study the growth of the p-rank of the Shafarevich–Tate group in cyclic degree-p extensions. One of our results on rank growth requires a mild hypothesis; we provide computational evidence for the same. The table is included in Section 6.
2 Preliminaries
Let F be a number field and
![]() $E_{/F}$
be an elliptic curve defined over F. Fix an algebraic closure of F and write
$E_{/F}$
be an elliptic curve defined over F. Fix an algebraic closure of F and write
![]() $G_F$
for the absolute Galois group
$G_F$
for the absolute Galois group
![]() $\operatorname {\mathrm {Gal}}(\overline {F}/F)$
. For a given integer m, set
$\operatorname {\mathrm {Gal}}(\overline {F}/F)$
. For a given integer m, set
![]() $E[m]$
to be the Galois module of all m-torsion points in
$E[m]$
to be the Galois module of all m-torsion points in
![]() $E(\overline {F})$
. If v is a prime in F, we write
$E(\overline {F})$
. If v is a prime in F, we write
![]() $F_v$
for the completion of F at v. The main object of interest is the Selmer group.
$F_v$
for the completion of F at v. The main object of interest is the Selmer group.
Definition 2.1. For any integer
![]() $m\geq 2$
, the m-Selmer group is defined as follows:
$m\geq 2$
, the m-Selmer group is defined as follows:
 $$ \begin{align*} \operatorname{\mathrm{Sel}}_{m}(E/F) = \ker\bigg( H^1( G_{F}, E[m]) \rightarrow \prod_{v}H^1(G_{F_v}, E )[m]\bigg). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Sel}}_{m}(E/F) = \ker\bigg( H^1( G_{F}, E[m]) \rightarrow \prod_{v}H^1(G_{F_v}, E )[m]\bigg). \end{align*} $$
This m-Selmer group fits into the following short exact sequence:
Here,
![]() is the Shafarevich–Tate group which is conjecturally finite. Throughout this article, we assume the finiteness of the Shafarevich–Tate group.
is the Shafarevich–Tate group which is conjecturally finite. Throughout this article, we assume the finiteness of the Shafarevich–Tate group.
2.1 Recollections from Iwasawa theory
For details, we refer the reader to standard texts in Iwasawa theory (for example, [Reference WashingtonWas97, Ch. 13]). Let p be a fixed prime. Consider the (unique) cyclotomic
![]() ${\mathbb Z}_p$
-extension of
${\mathbb Z}_p$
-extension of
![]() ${\mathbb Q}$
, denoted by
${\mathbb Q}$
, denoted by
![]() ${\mathbb Q}_{\operatorname {\mathrm {cyc}}}$
. Set
${\mathbb Q}_{\operatorname {\mathrm {cyc}}}$
. Set
![]() $\Gamma :=\operatorname {\mathrm {Gal}}({\mathbb Q}_{\operatorname {\mathrm {cyc}}}/{\mathbb Q})\simeq {\mathbb Z}_p$
. The Iwasawa algebra
$\Gamma :=\operatorname {\mathrm {Gal}}({\mathbb Q}_{\operatorname {\mathrm {cyc}}}/{\mathbb Q})\simeq {\mathbb Z}_p$
. The Iwasawa algebra
![]() $\Lambda $
is the completed group algebra
$\Lambda $
is the completed group algebra
![]() ${\mathbb Z}_p [\![ \Gamma ]\!] :=\varprojlim _n {\mathbb Z}_p[\Gamma /\Gamma ^{p^n}]$
. Fix a topological generator
${\mathbb Z}_p [\![ \Gamma ]\!] :=\varprojlim _n {\mathbb Z}_p[\Gamma /\Gamma ^{p^n}]$
. Fix a topological generator
![]() $\gamma $
of
$\gamma $
of
![]() $\Gamma $
; there is the following isomorphism of rings:
$\Gamma $
; there is the following isomorphism of rings:
 $$ \begin{align*} \Lambda&\xrightarrow{\sim}{\mathbb Z}_p [\![ T ]\!] \\ \gamma &\mapsto 1 +T. \end{align*} $$
$$ \begin{align*} \Lambda&\xrightarrow{\sim}{\mathbb Z}_p [\![ T ]\!] \\ \gamma &\mapsto 1 +T. \end{align*} $$
Let M be a cofinitely generated cotorsion
![]() $\Lambda $
-module. The structure theorem of
$\Lambda $
-module. The structure theorem of
![]() $\Lambda $
-modules asserts that the Pontryagin dual of M, denoted by
$\Lambda $
-modules asserts that the Pontryagin dual of M, denoted by
![]() $M^{\vee }$
, is pseudo-isomorphic to a finite direct sum of cyclic
$M^{\vee }$
, is pseudo-isomorphic to a finite direct sum of cyclic
![]() $\Lambda $
-modules. In other words, there is a map of
$\Lambda $
-modules. In other words, there is a map of
![]() $\Lambda $
-modules
$\Lambda $
-modules
 $$ \begin{align*} M^{\vee}\longrightarrow \bigg(\bigoplus_{i=1}^s \Lambda/(p^{m_i})\bigg)\oplus \bigg(\bigoplus_{j=1}^t \Lambda/(h_j(T)) \bigg) \end{align*} $$
$$ \begin{align*} M^{\vee}\longrightarrow \bigg(\bigoplus_{i=1}^s \Lambda/(p^{m_i})\bigg)\oplus \bigg(\bigoplus_{j=1}^t \Lambda/(h_j(T)) \bigg) \end{align*} $$
with finite kernel and cokernel. Here,
![]() $m_i>0$
and
$m_i>0$
and
![]() $h_j(T)$
is a distinguished polynomial (that is, a monic polynomial with nonleading coefficients divisible by p). The characteristic ideal of
$h_j(T)$
is a distinguished polynomial (that is, a monic polynomial with nonleading coefficients divisible by p). The characteristic ideal of
![]() $M^{\vee }$
is (up to a unit) generated by the characteristic element,
$M^{\vee }$
is (up to a unit) generated by the characteristic element,
 $$ \begin{align*} f_{M}^{(p)}(T) := p^{\sum_{i} m_i} \prod_j h_j(T). \end{align*} $$
$$ \begin{align*} f_{M}^{(p)}(T) := p^{\sum_{i} m_i} \prod_j h_j(T). \end{align*} $$
The
![]() $\mu $
-invariant of M is defined as the power of p in
$\mu $
-invariant of M is defined as the power of p in
![]() $f_{M}^{(p)}(T)$
. More precisely,
$f_{M}^{(p)}(T)$
. More precisely,
 $$ \begin{align*} \mu(M) = \mu_p(M):=\begin{cases}0 & \textrm{if } s=0,\\ \displaystyle\sum_{i=1}^s m_i & \textrm{if } s>0. \end{cases} \end{align*} $$
$$ \begin{align*} \mu(M) = \mu_p(M):=\begin{cases}0 & \textrm{if } s=0,\\ \displaystyle\sum_{i=1}^s m_i & \textrm{if } s>0. \end{cases} \end{align*} $$
The
![]() $\lambda $
-invariant of M is the degree of the characteristic element, that is,
$\lambda $
-invariant of M is the degree of the characteristic element, that is,
 $$ \begin{align*} \lambda(M) = \lambda_p(M) := \sum_{j=1}^t \deg h_j(T). \end{align*} $$
$$ \begin{align*} \lambda(M) = \lambda_p(M) := \sum_{j=1}^t \deg h_j(T). \end{align*} $$
Let
![]() $E_{/F}$
be an elliptic curve with good reduction at p. We assume throughout that the prime p is odd. Let
$E_{/F}$
be an elliptic curve with good reduction at p. We assume throughout that the prime p is odd. Let
![]() $N=N_E$
denote the conductor of E and denote by S the (finite) set of primes that divide
$N=N_E$
denote the conductor of E and denote by S the (finite) set of primes that divide
![]() $Np$
. Let
$Np$
. Let
![]() $F_S$
be the maximal algebraic extension of F that is unramified at the primes
$F_S$
be the maximal algebraic extension of F that is unramified at the primes
![]() $v\notin S$
. Set
$v\notin S$
. Set
![]() $E[p^{\infty }]$
to be the Galois module of all p-power torsion points in
$E[p^{\infty }]$
to be the Galois module of all p-power torsion points in
![]() $E(\overline {F})$
. For a prime
$E(\overline {F})$
. For a prime
![]() $v\in S$
and any finite extension
$v\in S$
and any finite extension
![]() $L/F$
contained in the unique cyclotomic
$L/F$
contained in the unique cyclotomic
![]() ${\mathbb Z}_p$
-extension of F (denoted by
${\mathbb Z}_p$
-extension of F (denoted by
![]() $F_{\operatorname {\mathrm {cyc}}}$
), write
$F_{\operatorname {\mathrm {cyc}}}$
), write
 $$ \begin{align*} J_v(E/L) = \bigoplus_{w|v} H^1( G_{L_w}, E)[p^{\infty}], \end{align*} $$
$$ \begin{align*} J_v(E/L) = \bigoplus_{w|v} H^1( G_{L_w}, E)[p^{\infty}], \end{align*} $$
where the direct sum is over all primes w of L lying above v. Then, the p-primary Selmer group over L is defined as follows:
 $$ \begin{align*} \operatorname{\mathrm{Sel}}_{p^{\infty}}(E/L):=\ker\bigg\{ H^1(\operatorname{\mathrm{Gal}}(F_S/L),E[p^{\infty}])\longrightarrow \bigoplus_{v\in S} J_v(E/L)\bigg\}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Sel}}_{p^{\infty}}(E/L):=\ker\bigg\{ H^1(\operatorname{\mathrm{Gal}}(F_S/L),E[p^{\infty}])\longrightarrow \bigoplus_{v\in S} J_v(E/L)\bigg\}. \end{align*} $$
It is easy to see that
![]() $\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/L) = \varinjlim _{n}\operatorname {\mathrm {Sel}}_{p^n}(E/L)$
, see for example [Reference Coates and SujathaCS00, Section 1.7]. By taking direct limits of Equation (2-1), the p-primary Selmer group over F fits into a short exact sequence,
$\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/L) = \varinjlim _{n}\operatorname {\mathrm {Sel}}_{p^n}(E/L)$
, see for example [Reference Coates and SujathaCS00, Section 1.7]. By taking direct limits of Equation (2-1), the p-primary Selmer group over F fits into a short exact sequence,
Next, define
where L ranges over finite extensions contained in
![]() $F_{\operatorname {\mathrm {cyc}}}$
and the inductive limit is taken with respect to the restriction maps. The p-primary Selmer group over
$F_{\operatorname {\mathrm {cyc}}}$
and the inductive limit is taken with respect to the restriction maps. The p-primary Selmer group over
![]() $F_{\operatorname {\mathrm {cyc}}}$
is defined as follows:
$F_{\operatorname {\mathrm {cyc}}}$
is defined as follows:
 $$ \begin{align*} \operatorname{\mathrm{Sel}}_{p^{\infty}}(E/F_{\operatorname{\mathrm{cyc}}}):=\ker\bigg\{ H^1(\operatorname{\mathrm{Gal}}(F_S/F_{\operatorname{\mathrm{cyc}}}),E[p^{\infty}])\longrightarrow \bigoplus_{v\in S} J_v(E/F_{\operatorname{\mathrm{cyc}}})\bigg\}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Sel}}_{p^{\infty}}(E/F_{\operatorname{\mathrm{cyc}}}):=\ker\bigg\{ H^1(\operatorname{\mathrm{Gal}}(F_S/F_{\operatorname{\mathrm{cyc}}}),E[p^{\infty}])\longrightarrow \bigoplus_{v\in S} J_v(E/F_{\operatorname{\mathrm{cyc}}})\bigg\}. \end{align*} $$
When E is an elliptic curve defined over
![]() ${\mathbb Q}$
, p is an odd prime of good ordinary reduction, and
${\mathbb Q}$
, p is an odd prime of good ordinary reduction, and
![]() $F/{\mathbb Q}$
is an abelian extension, K. Kato proved (see [Reference KatoKat04, Theorem 14.4]) that the p-primary Selmer group
$F/{\mathbb Q}$
is an abelian extension, K. Kato proved (see [Reference KatoKat04, Theorem 14.4]) that the p-primary Selmer group
![]() $\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/F_{\operatorname {\mathrm {cyc}}})$
is a cofinitely generated cotorsion
$\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/F_{\operatorname {\mathrm {cyc}}})$
is a cofinitely generated cotorsion
![]() $\Lambda $
-module. Therefore, in view of the structure theorem of
$\Lambda $
-module. Therefore, in view of the structure theorem of
![]() $\Lambda $
-modules, we can define the
$\Lambda $
-modules, we can define the
![]() $\mu $
and
$\mu $
and
![]() $\lambda $
-invariants, which we denote as
$\lambda $
-invariants, which we denote as
![]() $\mu _p(E/F)$
and
$\mu _p(E/F)$
and
![]() $\lambda _p(E/F)$
, respectively.
$\lambda _p(E/F)$
, respectively.
Given a number field F, we set
![]() $F_{\operatorname {\mathrm {cyc}}}$
to be the composite of F with
$F_{\operatorname {\mathrm {cyc}}}$
to be the composite of F with
![]() ${\mathbb Q}_{\operatorname {\mathrm {cyc}}}$
. It is the unique
${\mathbb Q}_{\operatorname {\mathrm {cyc}}}$
. It is the unique
![]() ${\mathbb Z}_p$
-extension of F that is contained in the infinite cyclotomic field
${\mathbb Z}_p$
-extension of F that is contained in the infinite cyclotomic field
![]() $F(\mu _{p^{\infty }})$
. Given
$F(\mu _{p^{\infty }})$
. Given
![]() $n\geq 0$
, let
$n\geq 0$
, let
![]() $F_n$
be the subfield of
$F_n$
be the subfield of
![]() $F_{\operatorname {\mathrm {cyc}}}$
such that
$F_{\operatorname {\mathrm {cyc}}}$
such that
![]() $[F_n:F]=p^n$
. The following lemma relating the
$[F_n:F]=p^n$
. The following lemma relating the
![]() $\lambda $
-invariant of the Selmer group to the rank of the elliptic curve is well known but we include it for the sake of completeness.
$\lambda $
-invariant of the Selmer group to the rank of the elliptic curve is well known but we include it for the sake of completeness.
Lemma 2.2. Let
![]() $E_{/F}$
be an elliptic curve and assume that
$E_{/F}$
be an elliptic curve and assume that
![]() $\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/F_{\operatorname {\mathrm {cyc}}})$
is cotorsion as a
$\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/F_{\operatorname {\mathrm {cyc}}})$
is cotorsion as a
![]() $\Lambda $
-module, and let
$\Lambda $
-module, and let
![]() $n\geq 0$
. Then,
$n\geq 0$
. Then,
![]() $\lambda _p(E/F)\geq \operatorname {\mathrm {rank}}_{{\mathbb Z}} (E(F_n))$
.
$\lambda _p(E/F)\geq \operatorname {\mathrm {rank}}_{{\mathbb Z}} (E(F_n))$
.
Proof. Denote by
![]() $\Gamma _n$
the Galois group
$\Gamma _n$
the Galois group
![]() $\operatorname {\mathrm {Gal}}(F_{\operatorname {\mathrm {cyc}}}/F_n)$
and let
$\operatorname {\mathrm {Gal}}(F_{\operatorname {\mathrm {cyc}}}/F_n)$
and let
![]() $r_n$
denote the
$r_n$
denote the
![]() ${\mathbb Z}_p$
-corank of
${\mathbb Z}_p$
-corank of
![]() $\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/F_{\operatorname {\mathrm {cyc}}})^{\Gamma _n}$
. Since
$\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/F_{\operatorname {\mathrm {cyc}}})^{\Gamma _n}$
. Since
![]() $\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/F_{\operatorname {\mathrm {cyc}}})$
is cotorsion over the Iwasawa algebra, it has finite
$\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/F_{\operatorname {\mathrm {cyc}}})$
is cotorsion over the Iwasawa algebra, it has finite
![]() ${\mathbb Z}_p$
-corank, and it is an easy consequence of the structure theorem that
${\mathbb Z}_p$
-corank, and it is an easy consequence of the structure theorem that
We deduce from Equation (2-2) that
with equality if
![]() is finite. It follows from the structure theory of
is finite. It follows from the structure theory of
![]() $\Lambda $
-modules that
$\Lambda $
-modules that
![]() $\lambda _p(E/F_n)\geq r_n$
. It suffices to show that
$\lambda _p(E/F_n)\geq r_n$
. It suffices to show that
![]() $r_n\geq \operatorname {\mathrm {rank}}_{{\mathbb Z}} (E(F_n))$
. This is indeed the case, since Mazur’s control theorem asserts that there is a natural map
$r_n\geq \operatorname {\mathrm {rank}}_{{\mathbb Z}} (E(F_n))$
. This is indeed the case, since Mazur’s control theorem asserts that there is a natural map
with finite kernel. From Equation (2-3), we see that
![]() $r_n\geq \operatorname {\mathrm {rank}}_{{\mathbb Z}} (E(F_n))$
and the result follows.
$r_n\geq \operatorname {\mathrm {rank}}_{{\mathbb Z}} (E(F_n))$
and the result follows.
Let
![]() $L/{\mathbb Q}$
be a degree-p Galois extension. The following theorem relates the
$L/{\mathbb Q}$
be a degree-p Galois extension. The following theorem relates the
![]() $\lambda $
-invariants of
$\lambda $
-invariants of
![]() $\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/{\mathbb Q}_{\operatorname {\mathrm {cyc}}})$
and
$\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/{\mathbb Q}_{\operatorname {\mathrm {cyc}}})$
and
![]() $\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/L_{\operatorname {\mathrm {cyc}}})$
.
$\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/L_{\operatorname {\mathrm {cyc}}})$
.
Theorem 2.3. Let
![]() $p\geq 5$
be a fixed prime. Let
$p\geq 5$
be a fixed prime. Let
![]() $L/{\mathbb Q}$
be a Galois extension of degree a power of p disjoint from the cyclotomic
$L/{\mathbb Q}$
be a Galois extension of degree a power of p disjoint from the cyclotomic
![]() ${\mathbb Z}_p$
-extension of
${\mathbb Z}_p$
-extension of
![]() ${\mathbb Q}$
. Let
${\mathbb Q}$
. Let
![]() $E_{/{\mathbb Q}}$
be a fixed elliptic curve with good ordinary reduction at p and suppose that
$E_{/{\mathbb Q}}$
be a fixed elliptic curve with good ordinary reduction at p and suppose that
![]() $\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/{\mathbb Q}_{\operatorname {\mathrm {cyc}}})$
is a cofinitely generated
$\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/{\mathbb Q}_{\operatorname {\mathrm {cyc}}})$
is a cofinitely generated
![]() ${\mathbb Z}_p$
-module. Then,
${\mathbb Z}_p$
-module. Then,
![]() $\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/L_{\operatorname {\mathrm {cyc}}})$
is also a cofinitely generated
$\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/L_{\operatorname {\mathrm {cyc}}})$
is also a cofinitely generated
![]() ${\mathbb Z}_p$
-module. Moreover, their respective
${\mathbb Z}_p$
-module. Moreover, their respective
![]() $\lambda $
-invariants are related by the following formula:
$\lambda $
-invariants are related by the following formula:
 $$ \begin{align*} \lambda_p(E/L) = p\lambda_p(E/{\mathbb Q}) + \sum_{w \in P_1} (e_{L_{\operatorname{\mathrm{cyc}}}/{\mathbb Q}_{\operatorname{\mathrm{cyc}}}}(w) -1 ) + 2\sum_{w\in P_2} (e_{L_{\operatorname{\mathrm{cyc}}}/{\mathbb Q}_{\operatorname{\mathrm{cyc}}}}(w) -1 ), \end{align*} $$
$$ \begin{align*} \lambda_p(E/L) = p\lambda_p(E/{\mathbb Q}) + \sum_{w \in P_1} (e_{L_{\operatorname{\mathrm{cyc}}}/{\mathbb Q}_{\operatorname{\mathrm{cyc}}}}(w) -1 ) + 2\sum_{w\in P_2} (e_{L_{\operatorname{\mathrm{cyc}}}/{\mathbb Q}_{\operatorname{\mathrm{cyc}}}}(w) -1 ), \end{align*} $$
where
![]() $e_{L_{\operatorname {\mathrm {cyc}}}/{\mathbb Q}_{\operatorname {\mathrm {cyc}}}}(w)$
is the ramification index, and
$e_{L_{\operatorname {\mathrm {cyc}}}/{\mathbb Q}_{\operatorname {\mathrm {cyc}}}}(w)$
is the ramification index, and
![]() $P_1, P_2$
are sets of primes in
$P_1, P_2$
are sets of primes in
![]() $L_{\operatorname {\mathrm {cyc}}}$
such that
$L_{\operatorname {\mathrm {cyc}}}$
such that
 $$ \begin{align*} P_1 & = \{ w : \ w\nmid p, \ E \textrm{ has split multiplicative reduction at }w \},\\ P_2 & = \{ w : \ w\nmid p, \ E \textrm{ has good reduction at }w, \ E(L_{\operatorname{\mathrm{cyc}},w}) \textrm{ has a point of order }p \}. \end{align*} $$
$$ \begin{align*} P_1 & = \{ w : \ w\nmid p, \ E \textrm{ has split multiplicative reduction at }w \},\\ P_2 & = \{ w : \ w\nmid p, \ E \textrm{ has good reduction at }w, \ E(L_{\operatorname{\mathrm{cyc}},w}) \textrm{ has a point of order }p \}. \end{align*} $$
Proof. [Reference Hachimori and MatsunoHM99, Theorem 3.1].
Remark 2.4. We remind the reader that a cofinitely generated cotorsion
![]() $\Lambda $
-module M is a cofinitely generated
$\Lambda $
-module M is a cofinitely generated
![]() ${\mathbb Z}_p$
-module precisely when the associated
${\mathbb Z}_p$
-module precisely when the associated
![]() $\mu $
-invariant is 0.
$\mu $
-invariant is 0.
We record the following result which was first proven by Greenberg.
Proposition 2.5. Let
![]() $E_{/{\mathbb Q}}$
be a rank 0 elliptic curve and assume that the Shafarevich–Tate group is finite. Then, for density one good (ordinary) primes,
$E_{/{\mathbb Q}}$
be a rank 0 elliptic curve and assume that the Shafarevich–Tate group is finite. Then, for density one good (ordinary) primes,
![]() $\mu _p(E/{\mathbb Q}) = \lambda _p(E/{\mathbb Q})= 0$
.
$\mu _p(E/{\mathbb Q}) = \lambda _p(E/{\mathbb Q})= 0$
.
Proof. See [Reference Greenberg and ViolaGre99, Theorem 5.1] or [Reference Kundu and RayKR21a, Theorem 3.7].
Remark 2.6. In [Reference Kundu and RayKR21a, Corollary 3.6], it is shown that
![]() $\mu _p(E/{\mathbb Q}) = \lambda _p(E/{\mathbb Q})= 0$
is equivalent to the vanishing of
$\mu _p(E/{\mathbb Q}) = \lambda _p(E/{\mathbb Q})= 0$
is equivalent to the vanishing of
![]() $\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/{\mathbb Q}_{\operatorname {\mathrm {cyc}}})$
. This happens when
$\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/{\mathbb Q}_{\operatorname {\mathrm {cyc}}})$
. This happens when
![]() $\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/{\mathbb Q})=0$
, the Tamagawa numbers at the primes of bad reduction of E are not divisible by p, and p is not an anomalous prime in the sense of [Reference MazurMaz72].
$\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/{\mathbb Q})=0$
, the Tamagawa numbers at the primes of bad reduction of E are not divisible by p, and p is not an anomalous prime in the sense of [Reference MazurMaz72].
2.2 Results, conjectures, and heuristics on ranks of elliptic curves
There are several important conjectures in the theory of elliptic curves. The first one of interest is the rank distribution conjecture which claims that over any number field, half of all elliptic curves (when ordered by height) have Mordell–Weil rank zero and the remaining half have Mordell–Weil rank one. Finally, higher Mordell–Weil ranks constitute zero percent of all elliptic curves, even though there may exist infinitely many such elliptic curves. Therefore, a suitably defined average rank would be
![]() $1/2$
. The best results in this direction are by Bhargava and Shankar (see [Reference Bhargava and ShankarBS15a, Reference Bhargava and ShankarBS15b]). They show that the average rank of elliptic curves over
$1/2$
. The best results in this direction are by Bhargava and Shankar (see [Reference Bhargava and ShankarBS15a, Reference Bhargava and ShankarBS15b]). They show that the average rank of elliptic curves over
![]() ${\mathbb Q}$
is strictly less than one, and that both rank zero and rank one cases comprise nonzero densities across all elliptic curves over
${\mathbb Q}$
is strictly less than one, and that both rank zero and rank one cases comprise nonzero densities across all elliptic curves over
![]() ${\mathbb Q}$
(see [Reference Bhargava and ShankarBS13]).
${\mathbb Q}$
(see [Reference Bhargava and ShankarBS13]).
Given an elliptic curve E defined over
![]() ${\mathbb Q}$
and base-changed to F, we have the associated Hasse–Weil L function,
${\mathbb Q}$
and base-changed to F, we have the associated Hasse–Weil L function,
![]() $L_E(s,F)$
. Let
$L_E(s,F)$
. Let
![]() $F/{\mathbb Q}$
be an abelian extension with Galois group G and conductor f. Let
$F/{\mathbb Q}$
be an abelian extension with Galois group G and conductor f. Let
![]() $\hat {G}$
be the group of Dirichlet characters,
$\hat {G}$
be the group of Dirichlet characters,
![]() $\chi : ({\mathbb Z}/f{\mathbb Z})^{\times } \rightarrow {\mathbb C}^{\times }$
. We further know that
$\chi : ({\mathbb Z}/f{\mathbb Z})^{\times } \rightarrow {\mathbb C}^{\times }$
. We further know that
 $$ \begin{align*} L_E(s, F) = \prod_{\chi\in \hat{G}}L_E(s,\chi), \end{align*} $$
$$ \begin{align*} L_E(s, F) = \prod_{\chi\in \hat{G}}L_E(s,\chi), \end{align*} $$
where the terms appearing on the right-hand side are the L-functions of
![]() $E_{/{\mathbb Q}}$
twisted by the character
$E_{/{\mathbb Q}}$
twisted by the character
![]() $\chi $
.
$\chi $
.
Conjecture 2.7 (Birch and Swinnerton-Dyer).
The Hasse–Weil L-function has analytic continuation to the whole complex plane, and
It follows from the Birch and Swinnerton-Dyer (BSD) conjecture that the vanishing of the twisted L-functions
![]() $L_E(s,\chi )$
at
$L_E(s,\chi )$
at
![]() $s=1$
is equivalent to the existence of rational points of infinite order on
$s=1$
is equivalent to the existence of rational points of infinite order on
![]() $E(F)$
.
$E(F)$
.
The following conjecture of David, Fearnley, and Kisilevsky predicts that given an elliptic curve over
![]() ${\mathbb Q}$
, the rank ‘rarely’ jumps in
${\mathbb Q}$
, the rank ‘rarely’ jumps in
![]() ${\mathbb Z}/p{\mathbb Z}$
-extensions with
${\mathbb Z}/p{\mathbb Z}$
-extensions with
![]() $p\neq 2$
. More precisely, we have the following conjecture.
$p\neq 2$
. More precisely, we have the following conjecture.
Conjecture 2.8 [Reference David, Fearnley, Kisilevsky, Conrey, Farmer, Mezzadri and SnaithDFK07, Conjecture 1.2].
Let p be an odd prime and
![]() $E_{/{\mathbb Q}}$
be an elliptic curve. Define
$E_{/{\mathbb Q}}$
be an elliptic curve. Define
-
(1) If
 $p=3$
, then as
$p=3$
, then as
 $X\rightarrow \infty $
,
$X\rightarrow \infty $
,  $$ \begin{align*} \log N_{E,p}(X) \sim \tfrac{1}{2}\log X. \end{align*} $$
$$ \begin{align*} \log N_{E,p}(X) \sim \tfrac{1}{2}\log X. \end{align*} $$
-
(2) If
 $p=5$
, then as
$p=5$
, then as
 $X\rightarrow \infty $
, the set
$X\rightarrow \infty $
, the set
 $N_{E,p}(X)$
is unbounded but
$N_{E,p}(X)$
is unbounded but
 $N_{E,p}(X)\ll X^{\epsilon }$
for any
$N_{E,p}(X)\ll X^{\epsilon }$
for any
 $\epsilon>0$
.
$\epsilon>0$
. -
(3) If
 $p\geq 7$
, then
$p\geq 7$
, then
 $N_{E,p}(X)$
is bounded.
$N_{E,p}(X)$
is bounded.
Under BSD,
![]() $\# N_{E,p}(X)$
can be rewritten as
$\# N_{E,p}(X)$
can be rewritten as
In [Reference DokchitserDok07, Theorem 1], T. Dokchitser showed that given an elliptic curve
![]() $E_{/{\mathbb Q}}$
, there are infinitely many
$E_{/{\mathbb Q}}$
, there are infinitely many
![]() ${\mathbb Z}/3{\mathbb Z}$
extensions where the rank jumps. More recently, B. Mazur and K. Rubin have shown (see [Reference Mazur, Rubin and LarsenMRL18, Theorem 1.2]) that given an elliptic curve E, there is a positive density set of primes (call it
${\mathbb Z}/3{\mathbb Z}$
extensions where the rank jumps. More recently, B. Mazur and K. Rubin have shown (see [Reference Mazur, Rubin and LarsenMRL18, Theorem 1.2]) that given an elliptic curve E, there is a positive density set of primes (call it
![]() $\mathcal {S}$
) such that for each
$\mathcal {S}$
) such that for each
![]() $p\in \mathcal {S}$
, there are infinitely many cyclic degree-p extensions over
$p\in \mathcal {S}$
, there are infinitely many cyclic degree-p extensions over
![]() ${\mathbb Q}$
with
${\mathbb Q}$
with
![]() $\operatorname {\mathrm {rank}}_{{\mathbb Z}}(E(L)) = \operatorname {\mathrm {rank}}_{{\mathbb Z}}(E({\mathbb Q}))$
. However, the result is unable to provide a positive proportion. Mazur and Rubin revisited this conjecture in a recent preprint (see [Reference Mazur and RubinMR19]) and their heuristics, based on the distribution of modular symbols, predicts the same statement as the conjecture of David, Fearnley, and Kisilevsky.
$\operatorname {\mathrm {rank}}_{{\mathbb Z}}(E(L)) = \operatorname {\mathrm {rank}}_{{\mathbb Z}}(E({\mathbb Q}))$
. However, the result is unable to provide a positive proportion. Mazur and Rubin revisited this conjecture in a recent preprint (see [Reference Mazur and RubinMR19]) and their heuristics, based on the distribution of modular symbols, predicts the same statement as the conjecture of David, Fearnley, and Kisilevsky.
3 Rank jump in degree-p Galois extensions
Let
![]() $E_{/{\mathbb Q}}$
be a rank 0 elliptic curve and p be an odd prime number. In this section, we are interested in studying two questions for a given pair
$E_{/{\mathbb Q}}$
be a rank 0 elliptic curve and p be an odd prime number. In this section, we are interested in studying two questions for a given pair
![]() $(E,p)$
. First, we analyze in how many (or what proportion of) cyclic degree-p Galois extensions over
$(E,p)$
. First, we analyze in how many (or what proportion of) cyclic degree-p Galois extensions over
![]() ${\mathbb Q}$
does the rank of E not jump. This question is addressed in Theorem 3.11: for non-CM elliptic curves, the result is unconditional; whereas for the CM-case, we prove the same result under an additional independence Hypothesis 3.10. Next, we study the dual problem, that is, for what proportion of elliptic curves does the rank not jump in at least one degree-p Galois extension over
${\mathbb Q}$
does the rank of E not jump. This question is addressed in Theorem 3.11: for non-CM elliptic curves, the result is unconditional; whereas for the CM-case, we prove the same result under an additional independence Hypothesis 3.10. Next, we study the dual problem, that is, for what proportion of elliptic curves does the rank not jump in at least one degree-p Galois extension over
![]() ${\mathbb Q}$
. This question is discussed in Section 3.2.
${\mathbb Q}$
. This question is discussed in Section 3.2.
Even though such questions have been studied in the past, our approach involving Iwasawa theory is new. Let
![]() $E_{/{\mathbb Q}}$
be an elliptic curve with good ordinary reduction at a fixed odd prime p. In Lemma 2.2, we show that over any number field,
$E_{/{\mathbb Q}}$
be an elliptic curve with good ordinary reduction at a fixed odd prime p. In Lemma 2.2, we show that over any number field,
![]() $\lambda _p(E/F)\geq \operatorname {\mathrm {rank}}_{{\mathbb Z}}(E(F))$
. It is well known (see for example [Reference Kundu and RayKR21a, Corollary 3.6]) that if
$\lambda _p(E/F)\geq \operatorname {\mathrm {rank}}_{{\mathbb Z}}(E(F))$
. It is well known (see for example [Reference Kundu and RayKR21a, Corollary 3.6]) that if
![]() $E_{/{\mathbb Q}}$
is a rank 0 elliptic curve with good (ordinary) reduction at an odd prime p, then
$E_{/{\mathbb Q}}$
is a rank 0 elliptic curve with good (ordinary) reduction at an odd prime p, then
![]() $\mu _p(E/{\mathbb Q}) = \lambda _p(E/{\mathbb Q}) = 0$
if and only if
$\mu _p(E/{\mathbb Q}) = \lambda _p(E/{\mathbb Q}) = 0$
if and only if
![]() $\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/{\mathbb Q}_{\operatorname {\mathrm {cyc}}}) =0$
. We remind the reader that in Proposition 2.5, we show that the triviality of
$\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/{\mathbb Q}_{\operatorname {\mathrm {cyc}}}) =0$
. We remind the reader that in Proposition 2.5, we show that the triviality of
![]() $\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/{\mathbb Q}_{\operatorname {\mathrm {cyc}}})$
is observed often. The same statement holds for any number field, under the additional hypothesis that the Shafarevich–Tate group is finite in every layer of its cyclotomic
$\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/{\mathbb Q}_{\operatorname {\mathrm {cyc}}})$
is observed often. The same statement holds for any number field, under the additional hypothesis that the Shafarevich–Tate group is finite in every layer of its cyclotomic
![]() ${\mathbb Z}_p$
-extension. Our key idea is to start with a rank 0 elliptic curve
${\mathbb Z}_p$
-extension. Our key idea is to start with a rank 0 elliptic curve
![]() $E_{/{\mathbb Q}}$
for which
$E_{/{\mathbb Q}}$
for which
![]() $\mu _p(E/{\mathbb Q}) = \lambda _p(E/{\mathbb Q})=0$
and count how often
$\mu _p(E/{\mathbb Q}) = \lambda _p(E/{\mathbb Q})=0$
and count how often
![]() $\mu _p(E/L) = \lambda _p(E/L) =0$
, where
$\mu _p(E/L) = \lambda _p(E/L) =0$
, where
![]() $L/{\mathbb Q}$
is a cyclic degree-p extension.
$L/{\mathbb Q}$
is a cyclic degree-p extension.
For a number field F, it is possible that
![]() $\lambda _p(E/F)> \operatorname {\mathrm {rank}}_{{\mathbb Z}}(E(F))$
. So, our method fails to measure all instances when the rank of the elliptic curve does not change; that is, our results only provide a lower bound. However, we succeed in answering a stronger question, that is, how often the p-primary Selmer group
$\lambda _p(E/F)> \operatorname {\mathrm {rank}}_{{\mathbb Z}}(E(F))$
. So, our method fails to measure all instances when the rank of the elliptic curve does not change; that is, our results only provide a lower bound. However, we succeed in answering a stronger question, that is, how often the p-primary Selmer group
![]() $\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/F_{\operatorname {\mathrm {cyc}}})$
is trivial upon base-change.
$\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/F_{\operatorname {\mathrm {cyc}}})$
is trivial upon base-change.
3.1
Let
![]() $E_{/{\mathbb Q}}$
be a fixed rank 0 elliptic curve of conductor N with good ordinary reduction at a fixed prime
$E_{/{\mathbb Q}}$
be a fixed rank 0 elliptic curve of conductor N with good ordinary reduction at a fixed prime
![]() $p\geq 5$
such that
$p\geq 5$
such that
![]() $\mu _p(E/{\mathbb Q}) = \lambda _p(E/{\mathbb Q})=0$
. Recall that the rank distribution conjecture predicts that half of the elliptic curves (ordered by height or conductor) have rank 0. Moreover, Proposition 2.5 asserts that there are density one good ordinary primes satisfying the condition of vanishing Iwasawa invariants. Lastly, when an elliptic curve does not have CM, density one of the primes are good ordinary; in the CM case, the good ordinary and the good supersingular primes each have density 1/2.
$\mu _p(E/{\mathbb Q}) = \lambda _p(E/{\mathbb Q})=0$
. Recall that the rank distribution conjecture predicts that half of the elliptic curves (ordered by height or conductor) have rank 0. Moreover, Proposition 2.5 asserts that there are density one good ordinary primes satisfying the condition of vanishing Iwasawa invariants. Lastly, when an elliptic curve does not have CM, density one of the primes are good ordinary; in the CM case, the good ordinary and the good supersingular primes each have density 1/2.
Throughout this section,
![]() $L/{\mathbb Q}$
denotes a
$L/{\mathbb Q}$
denotes a
![]() ${\mathbb Z}/p{\mathbb Z}$
-extension disjoint from the cyclotomic
${\mathbb Z}/p{\mathbb Z}$
-extension disjoint from the cyclotomic
![]() ${\mathbb Z}_p$
-extension. Let q be a prime number distinct from p such that E has good reduction at q, that is,
${\mathbb Z}_p$
-extension. Let q be a prime number distinct from p such that E has good reduction at q, that is,
![]() $\gcd (q,N)=1$
. Let
$\gcd (q,N)=1$
. Let
![]() $w|q$
be a prime in L,
$w|q$
be a prime in L,
![]() $L_w$
be the completion at w, and
$L_w$
be the completion at w, and
![]() $\kappa $
be the residue field of characteristic q. We know that there is an exact sequence of abelian groups (see [Reference SilvermanSil09, Proposition VII.2.1]),
$\kappa $
be the residue field of characteristic q. We know that there is an exact sequence of abelian groups (see [Reference SilvermanSil09, Proposition VII.2.1]),
where
![]() $\widetilde {E}_{\operatorname {\mathrm {ns}}}(\kappa )$
is the set of nonsingular points of the reduced elliptic curve,
$\widetilde {E}_{\operatorname {\mathrm {ns}}}(\kappa )$
is the set of nonsingular points of the reduced elliptic curve,
![]() $E_0(L_w)$
is the set of points with nonsingular reduction, and
$E_0(L_w)$
is the set of points with nonsingular reduction, and
![]() $E_1(L_w)$
is the kernel of the reduction map. Since
$E_1(L_w)$
is the kernel of the reduction map. Since
![]() $p\neq q$
, we know that
$p\neq q$
, we know that
![]() $E_1(L_w)[p]$
is trivial (see [Reference SilvermanSil09, VII.3.1]). Because q is assumed to be a prime of good reduction,
$E_1(L_w)[p]$
is trivial (see [Reference SilvermanSil09, VII.3.1]). Because q is assumed to be a prime of good reduction,
![]() $E_0(L_w) = E(L_w)$
. Hence,
$E_0(L_w) = E(L_w)$
. Hence,
Since
![]() $L/{\mathbb Q}$
is a
$L/{\mathbb Q}$
is a
![]() ${\mathbb Z}/p{\mathbb Z}$
-extension, the residue field is either
${\mathbb Z}/p{\mathbb Z}$
-extension, the residue field is either
![]() $\mathbb {F}_{q^p}$
or
$\mathbb {F}_{q^p}$
or
![]() $\mathbb {F}_{q}$
depending on whether q is inert in the extension or not.
$\mathbb {F}_{q}$
depending on whether q is inert in the extension or not.
As explained above, (under standard hypotheses) we know that
![]() $\lambda _p(E/L)\geq \operatorname {\mathrm {rank}}_{{\mathbb Z}}(E(L))$
. Since we have assumed that
$\lambda _p(E/L)\geq \operatorname {\mathrm {rank}}_{{\mathbb Z}}(E(L))$
. Since we have assumed that
![]() $\mu _p(E/{\mathbb Q})=0$
, it follows from Theorem 2.3 that
$\mu _p(E/{\mathbb Q})=0$
, it follows from Theorem 2.3 that
![]() $\mu _p(E/L)=0$
. To show that
$\mu _p(E/L)=0$
. To show that
![]() $\lambda _p(E/L)=0$
, it suffices to show that
$\lambda _p(E/L)=0$
, it suffices to show that
 $$ \begin{align*} \sum_{w\in P_1} ( e_{L_{\operatorname{\mathrm{cyc}}}/{\mathbb Q}_{\operatorname{\mathrm{cyc}}}}(w) -1) = \sum_{w\in P_2} ( e_{L_{\operatorname{\mathrm{cyc}}}/{\mathbb Q}_{\operatorname{\mathrm{cyc}}}}(w) -1)=0. \end{align*} $$
$$ \begin{align*} \sum_{w\in P_1} ( e_{L_{\operatorname{\mathrm{cyc}}}/{\mathbb Q}_{\operatorname{\mathrm{cyc}}}}(w) -1) = \sum_{w\in P_2} ( e_{L_{\operatorname{\mathrm{cyc}}}/{\mathbb Q}_{\operatorname{\mathrm{cyc}}}}(w) -1)=0. \end{align*} $$
Recall that all primes in the cyclotomic
![]() ${\mathbb Z}_p$
-extension are finitely decomposed and the only primes that ramify are those above p. Moreover,
${\mathbb Z}_p$
-extension are finitely decomposed and the only primes that ramify are those above p. Moreover,
![]() $L\cap {\mathbb Q}_{\operatorname {\mathrm {cyc}}} ={\mathbb Q}$
and
$L\cap {\mathbb Q}_{\operatorname {\mathrm {cyc}}} ={\mathbb Q}$
and
![]() $p\not \in P_1 \cup P_2$
(recall the definition of these sets from Theorem 2.3). Therefore,
$p\not \in P_1 \cup P_2$
(recall the definition of these sets from Theorem 2.3). Therefore,
![]() $e_{L_{\operatorname {\mathrm {cyc}}}/{\mathbb Q}_{\operatorname {\mathrm {cyc}}}} = e_{L/{\mathbb Q}}$
. Since
$e_{L_{\operatorname {\mathrm {cyc}}}/{\mathbb Q}_{\operatorname {\mathrm {cyc}}}} = e_{L/{\mathbb Q}}$
. Since
![]() $p\geq 5$
, the reduction type does not change upon base-change. In particular, if
$p\geq 5$
, the reduction type does not change upon base-change. In particular, if
![]() $q(\neq p)$
is a prime of additive reduction for
$q(\neq p)$
is a prime of additive reduction for
![]() $E_{/{\mathbb Q}}$
, then it has additive reduction over
$E_{/{\mathbb Q}}$
, then it has additive reduction over
![]() $L_{\operatorname {\mathrm {cyc}}}$
(see [Reference Serre and TateST68, page 498] or [Reference Hachimori and MatsunoHM99, page 587]). Finally, since
$L_{\operatorname {\mathrm {cyc}}}$
(see [Reference Serre and TateST68, page 498] or [Reference Hachimori and MatsunoHM99, page 587]). Finally, since
![]() $L_{\operatorname {\mathrm {cyc}},w}/L_w$
is a pro-p group, we have that
$L_{\operatorname {\mathrm {cyc}},w}/L_w$
is a pro-p group, we have that
![]() $E(L_{\operatorname {\mathrm {cyc}},w})[p^{\infty }]=0$
if and only if
$E(L_{\operatorname {\mathrm {cyc}},w})[p^{\infty }]=0$
if and only if
![]() $E(L_{w})[p^{\infty }]=0$
. Thus, it suffices to show that
$E(L_{w})[p^{\infty }]=0$
. Thus, it suffices to show that
 $$ \begin{align} \sum_{w\in P_1} ( e_{L/{\mathbb Q}}(w) -1) = \sum_{w\in P_2} ( e_{L/{\mathbb Q}}(w) -1)=0, \end{align} $$
$$ \begin{align} \sum_{w\in P_1} ( e_{L/{\mathbb Q}}(w) -1) = \sum_{w\in P_2} ( e_{L/{\mathbb Q}}(w) -1)=0, \end{align} $$
where
![]() $P_1, P_2$
are now sets of primes in L. More precisely,
$P_1, P_2$
are now sets of primes in L. More precisely,
 $$ \begin{align*} P_1 & = \{ w\in L : \ w\nmid p, \ E \textrm{ has split multiplicative reduction at }w \},\\ P_2 & = \{ w\in L : \ w\nmid p, \ E \textrm{ has good reduction at }w, \ E(L_{w}) \textrm{ has a point of order }p \}. \end{align*} $$
$$ \begin{align*} P_1 & = \{ w\in L : \ w\nmid p, \ E \textrm{ has split multiplicative reduction at }w \},\\ P_2 & = \{ w\in L : \ w\nmid p, \ E \textrm{ has good reduction at }w, \ E(L_{w}) \textrm{ has a point of order }p \}. \end{align*} $$
It is often possible that
![]() $P_1 = \emptyset $
but the set
$P_1 = \emptyset $
but the set
![]() $P_2$
is never empty. In fact, it is known that (see for example [Reference CojocaruCoj04, Section 2])
$P_2$
is never empty. In fact, it is known that (see for example [Reference CojocaruCoj04, Section 2])
 $$ \begin{align*} \lim_{X\rightarrow\infty} \frac{\# \{q \leq X \mid q\nmid pN, \ p\mid \#\widetilde{E}({\mathbb F}_q)\}}{\pi(X)} \approx \frac{1}{p}. \end{align*} $$
$$ \begin{align*} \lim_{X\rightarrow\infty} \frac{\# \{q \leq X \mid q\nmid pN, \ p\mid \#\widetilde{E}({\mathbb F}_q)\}}{\pi(X)} \approx \frac{1}{p}. \end{align*} $$
Here,
![]() $\pi (X)$
is the prime counting function.
$\pi (X)$
is the prime counting function.
Remark 3.1. Henceforth, the sets
![]() $P_1, P_2$
will denote sets of primes in L (rather than
$P_1, P_2$
will denote sets of primes in L (rather than
![]() $L_{\operatorname {\mathrm {cyc}}}$
). By our assumption that
$L_{\operatorname {\mathrm {cyc}}}$
). By our assumption that
![]() $L\cap {\mathbb Q}_{\operatorname {\mathrm {cyc}}}={\mathbb Q}$
, we have excluded the case that p is the only ramified prime. If two or more primes are ramified, then it is possible that p is (wildly) ramified in L. However, by definition,
$L\cap {\mathbb Q}_{\operatorname {\mathrm {cyc}}}={\mathbb Q}$
, we have excluded the case that p is the only ramified prime. If two or more primes are ramified, then it is possible that p is (wildly) ramified in L. However, by definition,
![]() $p\not \in P_1\cup P_2$
. Therefore, the ramification of p in
$p\not \in P_1\cup P_2$
. Therefore, the ramification of p in
![]() $L/{\mathbb Q}$
does not contribute to the
$L/{\mathbb Q}$
does not contribute to the
![]() $\lambda $
-jump. It suffices to focus on the ramification of primes
$\lambda $
-jump. It suffices to focus on the ramification of primes
![]() $q\neq p$
.
$q\neq p$
.
The above discussion can be summarized in the result below.
Proposition 3.2. Let
![]() $E_{/{\mathbb Q}}$
be a rank 0 elliptic curve with good ordinary reduction at
$E_{/{\mathbb Q}}$
be a rank 0 elliptic curve with good ordinary reduction at
![]() $p\geq 5$
such that
$p\geq 5$
such that
![]() $\mu _p(E/{\mathbb Q})=\lambda _p(E/{\mathbb Q})=0$
. Let
$\mu _p(E/{\mathbb Q})=\lambda _p(E/{\mathbb Q})=0$
. Let
![]() $L/{\mathbb Q}$
be any cyclic degree-p extension disjoint from
$L/{\mathbb Q}$
be any cyclic degree-p extension disjoint from
![]() ${\mathbb Q}_{\operatorname {\mathrm {cyc}}}$
such that Equation (3-1) holds. Then,
${\mathbb Q}_{\operatorname {\mathrm {cyc}}}$
such that Equation (3-1) holds. Then,
![]() $\mu _p(E/L) = \lambda _p(E/L)=0$
. This implies in particular that
$\mu _p(E/L) = \lambda _p(E/L)=0$
. This implies in particular that
![]() $\operatorname {\mathrm {rank}}_{{\mathbb Z}}( E(L_n))=0$
for all
$\operatorname {\mathrm {rank}}_{{\mathbb Z}}( E(L_n))=0$
for all
![]() $n\geq 0$
.
$n\geq 0$
.
The conditions imposed in Proposition 3.2 will be required throughout this section. Therefore, we make the following definition.
Definition 3.3. Given an elliptic curve
![]() $E_{/{\mathbb Q}}$
of rank 0, a prime p is called irrelevant if at least one of the following properties hold.
$E_{/{\mathbb Q}}$
of rank 0, a prime p is called irrelevant if at least one of the following properties hold.
-
(i) p is a prime of bad reduction.
-
(ii) p is a prime of supersingular reduction.
-
(iii) At p, the
 $\mu $
-invariant associated to the p-primary Selmer group is positive.
$\mu $
-invariant associated to the p-primary Selmer group is positive. -
(iv) At p, the
 $\lambda $
-invariant associated to the p-primary Selmer group is positive.
$\lambda $
-invariant associated to the p-primary Selmer group is positive.
Otherwise, it is called a relevant prime.
Let E be an elliptic curve and let
![]() $p,q$
be two distinct primes. Given a triple
$p,q$
be two distinct primes. Given a triple
![]() $(E, p, q)$
, we aim to understand when Equation (3-1) holds. We begin by recalling the following well-known result.
$(E, p, q)$
, we aim to understand when Equation (3-1) holds. We begin by recalling the following well-known result.
Proposition 3.4. Let p be an odd prime. Let
![]() $L/{\mathbb Q}$
be any
$L/{\mathbb Q}$
be any
![]() ${\mathbb Z}/p{\mathbb Z}$
-extension disjoint from the cyclotomic
${\mathbb Z}/p{\mathbb Z}$
-extension disjoint from the cyclotomic
![]() ${\mathbb Z}_p$
-extension that is ramified at exactly one prime
${\mathbb Z}_p$
-extension that is ramified at exactly one prime
![]() $q\neq p$
. Such an extension exists precisely when
$q\neq p$
. Such an extension exists precisely when
![]() $q \equiv 1 \ \pmod {\,p}$
. Moreover, L is unique and has conductor q.
$q \equiv 1 \ \pmod {\,p}$
. Moreover, L is unique and has conductor q.
Proof. See for example [Reference Jones, Roberts, van der Poorten and SteinJR08, Proposition 1.1].
In fact, it follows from class field theory (see [Reference Mantilla-Soler and MonsurròMSM16, Lemma 2.5]) that the primes that ramify in a
![]() ${\mathbb Z}/p{\mathbb Z}$
-extension are either p or precisely those of the form
${\mathbb Z}/p{\mathbb Z}$
-extension are either p or precisely those of the form
![]() $q\equiv 1\ \pmod {\,p}$
. By local class field theory, the discriminant of
$q\equiv 1\ \pmod {\,p}$
. By local class field theory, the discriminant of
![]() $L/{\mathbb Q}$
(denoted
$L/{\mathbb Q}$
(denoted
![]() $d(L/{\mathbb Q})$
) is given by (see [Reference Mantilla-Soler and MonsurròMSM16, Lemma 2.4])
$d(L/{\mathbb Q})$
) is given by (see [Reference Mantilla-Soler and MonsurròMSM16, Lemma 2.4])
 $$ \begin{align*} d(L/{\mathbb Q}) = \begin{cases} \displaystyle\prod_{i=1}^r q_i^{p-1} & \textrm{if }q_i \textrm{ is ramified,}\\ \displaystyle\prod_{i=1}^r q_i^{p-1}p^{2(p-1)} & \textrm{if }q_i \textrm{ and } p \textrm{ are ramified.} \end{cases} \end{align*} $$
$$ \begin{align*} d(L/{\mathbb Q}) = \begin{cases} \displaystyle\prod_{i=1}^r q_i^{p-1} & \textrm{if }q_i \textrm{ is ramified,}\\ \displaystyle\prod_{i=1}^r q_i^{p-1}p^{2(p-1)} & \textrm{if }q_i \textrm{ and } p \textrm{ are ramified.} \end{cases} \end{align*} $$
If
![]() $q\ (\neq p)$
ramifies in a
$q\ (\neq p)$
ramifies in a
![]() ${\mathbb Z}/p$
-extension, then the ramification is tame.
${\mathbb Z}/p$
-extension, then the ramification is tame.
For primes of the form
![]() $q\equiv 1\ \pmod {\,p}$
(that is, primes that can ramify in
$q\equiv 1\ \pmod {\,p}$
(that is, primes that can ramify in
![]() ${\mathbb Z}/p{\mathbb Z}$
-extensions), we introduce the notion of friendly and enemy primes.
${\mathbb Z}/p{\mathbb Z}$
-extensions), we introduce the notion of friendly and enemy primes.
Definition 3.5. Let p be a fixed odd prime and
![]() $E_{/{\mathbb Q}}$
be a fixed elliptic curve of rank 0 for which p is a relevant prime (see Definition 3.3). Define enemy primes to be those primes that are of the form
$E_{/{\mathbb Q}}$
be a fixed elliptic curve of rank 0 for which p is a relevant prime (see Definition 3.3). Define enemy primes to be those primes that are of the form
![]() $q\equiv 1\ \pmod {\,p}$
and such that either of the following conditions hold:
$q\equiv 1\ \pmod {\,p}$
and such that either of the following conditions hold:
-
(i) q is a prime of split multiplicative reduction; or
-
(ii) q is a prime of good reduction and
 $p \mid \# \widetilde {E}(\mathbb {F}_q)$
.
$p \mid \# \widetilde {E}(\mathbb {F}_q)$
.
If a prime is of the form
![]() $q\equiv 1 \ \pmod {\,p}$
with the additional properties that q is a prime of good reduction and
$q\equiv 1 \ \pmod {\,p}$
with the additional properties that q is a prime of good reduction and
![]() $p\nmid \#\widetilde {E}(\mathbb {F}_q)$
, then q will be called friendly.
$p\nmid \#\widetilde {E}(\mathbb {F}_q)$
, then q will be called friendly.
Remark 3.6
-
(i) A prime
 $q\equiv 1\ \pmod {\,p}$
that is a prime of bad reduction but not of split multiplicative type is neither an enemy prime nor a friendly prime.
$q\equiv 1\ \pmod {\,p}$
that is a prime of bad reduction but not of split multiplicative type is neither an enemy prime nor a friendly prime. -
(ii) For our purpose, it is enough to work with the residue field
 $\mathbb {F}_q$
because, eventually, we want the primes q to ramify in the extension L.
$\mathbb {F}_q$
because, eventually, we want the primes q to ramify in the extension L.
Primes
![]() $w|q$
in L will also be called an enemy or a friendly prime depending on the behavior of q. The following lemma will play a crucial role in the subsequent discussion.
$w|q$
in L will also be called an enemy or a friendly prime depending on the behavior of q. The following lemma will play a crucial role in the subsequent discussion.
Lemma 3.7. Let
![]() $L/{\mathbb Q}$
be a cyclic degree-p extension disjoint from
$L/{\mathbb Q}$
be a cyclic degree-p extension disjoint from
![]() ${\mathbb Q}_{\operatorname {\mathrm {cyc}}}$
. Then, Equation (3-1) holds precisely when no ramified prime is an enemy prime.
${\mathbb Q}_{\operatorname {\mathrm {cyc}}}$
. Then, Equation (3-1) holds precisely when no ramified prime is an enemy prime.
Proof. Recall that
![]() $P_1$
consists of primes
$P_1$
consists of primes
![]() $w\nmid p$
such that E has split multiplicative reduction at w. Observe that
$w\nmid p$
such that E has split multiplicative reduction at w. Observe that
 $$ \begin{align*} \sum_{w\in P_1}( e_{L/{\mathbb Q}}(w) -1 ) \neq 0 \end{align*} $$
$$ \begin{align*} \sum_{w\in P_1}( e_{L/{\mathbb Q}}(w) -1 ) \neq 0 \end{align*} $$
if and only if there exists a ramified prime in
![]() $L/{\mathbb Q}$
of split multiplicative type. The assertion is immediate from the definition of an enemy prime.
$L/{\mathbb Q}$
of split multiplicative type. The assertion is immediate from the definition of an enemy prime.
Since L is disjoint from
![]() ${\mathbb Q}_{\operatorname {\mathrm {cyc}}}$
, we know that if p is ramified in
${\mathbb Q}_{\operatorname {\mathrm {cyc}}}$
, we know that if p is ramified in
![]() $L/{\mathbb Q}$
, there must be at least one other prime that is also ramified. Now,
$L/{\mathbb Q}$
, there must be at least one other prime that is also ramified. Now,
 $$ \begin{align*} \sum_{w\in P_2}( e_{L/{\mathbb Q}}(w) -1 )\neq 0 \end{align*} $$
$$ \begin{align*} \sum_{w\in P_2}( e_{L/{\mathbb Q}}(w) -1 )\neq 0 \end{align*} $$
precisely when there exists a
![]() $q\ (\neq p)$
satisfying all of the following conditions:
$q\ (\neq p)$
satisfying all of the following conditions:
-
(i) q is a prime of good reduction for E;
-
(ii) q is ramified in the extension
 $L/{\mathbb Q}$
; and
$L/{\mathbb Q}$
; and -
(iii) w is a prime above q with
 $E(L_w)[p]\neq 0$
.
$E(L_w)[p]\neq 0$
.
The conclusion of the lemma is now straightforward.
3.1.1
For a given pair
![]() $(E,p)$
, we denote the set of enemy primes by
$(E,p)$
, we denote the set of enemy primes by
![]() ${\mathcal E}_{(E,p)}$
and the set of friendly primes by
${\mathcal E}_{(E,p)}$
and the set of friendly primes by
![]() ${\mathcal F}_{(E,p)}$
. Write
${\mathcal F}_{(E,p)}$
. Write
![]() $\mathcal {N}_{(E,p)}$
for the set of primes of the form
$\mathcal {N}_{(E,p)}$
for the set of primes of the form
![]() $q\equiv 1\ \pmod {\,p}$
, where E has bad reduction not of split multiplicative type. The three sets are disjoint. We further subdivide the first two of these sets into disjoint sets, namely
$q\equiv 1\ \pmod {\,p}$
, where E has bad reduction not of split multiplicative type. The three sets are disjoint. We further subdivide the first two of these sets into disjoint sets, namely
 $$ \begin{align*} {\mathcal F}_{(E,p)} &= {\mathcal F}_{(E,p)}^{\operatorname{\mathrm{ord}}} \cup {\mathcal F}_{(E,p)}^{\operatorname{\mathrm{ss}}} \textrm{ and }\\ {\mathcal E}_{(E,p)} &= {\mathcal E}_{(E,p)}^{\operatorname{\mathrm{split}}} \cup {\mathcal E}_{(E,p)}^{\operatorname{\mathrm{ord}}} \cup {\mathcal E}_{(E,p)}^{\operatorname{\mathrm{ss}}}. \end{align*} $$
$$ \begin{align*} {\mathcal F}_{(E,p)} &= {\mathcal F}_{(E,p)}^{\operatorname{\mathrm{ord}}} \cup {\mathcal F}_{(E,p)}^{\operatorname{\mathrm{ss}}} \textrm{ and }\\ {\mathcal E}_{(E,p)} &= {\mathcal E}_{(E,p)}^{\operatorname{\mathrm{split}}} \cup {\mathcal E}_{(E,p)}^{\operatorname{\mathrm{ord}}} \cup {\mathcal E}_{(E,p)}^{\operatorname{\mathrm{ss}}}. \end{align*} $$
Here,
![]() ${\mathcal F}_{(E,p)}^{\operatorname {\mathrm {ord}}}$
(respectively
${\mathcal F}_{(E,p)}^{\operatorname {\mathrm {ord}}}$
(respectively
![]() ${\mathcal F}_{(E,p)}^{\operatorname {\mathrm {ss}}}$
) is the set of primes of the form
${\mathcal F}_{(E,p)}^{\operatorname {\mathrm {ss}}}$
) is the set of primes of the form
![]() $q\equiv 1 \ \pmod {\,p}$
such that q is a prime of good ordinary (respectively supersingular) reduction and
$q\equiv 1 \ \pmod {\,p}$
such that q is a prime of good ordinary (respectively supersingular) reduction and
![]() $p\nmid \#\widetilde {E}({\mathbb F}_q)$
. The set
$p\nmid \#\widetilde {E}({\mathbb F}_q)$
. The set
![]() ${\mathcal E}_{(E,p)}^{\operatorname {\mathrm {split}}}$
consists of all the primes
${\mathcal E}_{(E,p)}^{\operatorname {\mathrm {split}}}$
consists of all the primes
![]() $q \equiv 1\,\mod {p}$
of split multiplicative reduction. Finally,
$q \equiv 1\,\mod {p}$
of split multiplicative reduction. Finally,
![]() ${\mathcal E}_{(E,p)}^{\operatorname {\mathrm {ord}}}$
(respectively
${\mathcal E}_{(E,p)}^{\operatorname {\mathrm {ord}}}$
(respectively
![]() ${\mathcal E}_{(E,p)}^{\operatorname {\mathrm {ss}}}$
) is the set of primes of the form
${\mathcal E}_{(E,p)}^{\operatorname {\mathrm {ss}}}$
) is the set of primes of the form
![]() $q\equiv 1 \ \pmod {\,p}$
such that q is a prime of good ordinary (respectively supersingular) reduction and
$q\equiv 1 \ \pmod {\,p}$
such that q is a prime of good ordinary (respectively supersingular) reduction and
![]() $p| \#\widetilde {E}({\mathbb F}_q)$
.
$p| \#\widetilde {E}({\mathbb F}_q)$
.
Lemma 3.8. Let
![]() $E_{/{\mathbb Q}}$
be an elliptic curve and
$E_{/{\mathbb Q}}$
be an elliptic curve and
![]() $p\geq 5$
be a relevant prime. Then,
$p\geq 5$
be a relevant prime. Then,
![]() ${\mathcal E}_{(E,p)}^{\operatorname {\mathrm {ss}}} = \emptyset $
. In particular,
${\mathcal E}_{(E,p)}^{\operatorname {\mathrm {ss}}} = \emptyset $
. In particular,
![]() ${\mathcal E}_{(E,p)} = {\mathcal E}_{(E,p)}^{\operatorname {\mathrm {split}}} \cup {\mathcal E}_{(E,p)}^{\operatorname {\mathrm {ord}}}$
.
${\mathcal E}_{(E,p)} = {\mathcal E}_{(E,p)}^{\operatorname {\mathrm {split}}} \cup {\mathcal E}_{(E,p)}^{\operatorname {\mathrm {ord}}}$
.
Proof. When
![]() $q \geq 7$
is a prime of supersingular reduction, then it follows from the Hasse bound that
$q \geq 7$
is a prime of supersingular reduction, then it follows from the Hasse bound that
![]() $a_q =0$
. Therefore,
$a_q =0$
. Therefore,
Note that we require that
![]() $q \equiv 1\ \pmod {\,p}$
. Thus,
$q \equiv 1\ \pmod {\,p}$
. Thus,
![]() $p \nmid \# \widetilde {E}({\mathbb F}_q)$
.
$p \nmid \# \widetilde {E}({\mathbb F}_q)$
.
For any subset
![]() $\mathcal {S}'$
of the set of primes, let
$\mathcal {S}'$
of the set of primes, let
![]() $\mathfrak {d}(\mathcal {S}')$
denote the Dirichlet density of
$\mathfrak {d}(\mathcal {S}')$
denote the Dirichlet density of
![]() $\mathcal {S}'$
. With notation as above, we have that
$\mathcal {S}'$
. With notation as above, we have that
 $$ \begin{align} \mathfrak{d}({\mathcal E}_{(E,p)}) + \mathfrak{d}({\mathcal F}_{(E,p)}) + \mathfrak{d}(\mathcal{N}_{(E,p)})= \frac{1}{\varphi(p)} = \frac{1}{p-1}. \end{align} $$
$$ \begin{align} \mathfrak{d}({\mathcal E}_{(E,p)}) + \mathfrak{d}({\mathcal F}_{(E,p)}) + \mathfrak{d}(\mathcal{N}_{(E,p)})= \frac{1}{\varphi(p)} = \frac{1}{p-1}. \end{align} $$
The first equality follows from Dirichlet’s theorem on primes in arithmetic progressions, which asserts that the proportion of primes that are congruent to
![]() $1$
modulo p is
$1$
modulo p is
![]() $1/\varphi (p)$
. The set
$1/\varphi (p)$
. The set
![]() $\mathcal {N}_{(E,p)}$
is finite, and hence
$\mathcal {N}_{(E,p)}$
is finite, and hence
![]() $\mathfrak {d}(\mathcal {N}_{(E,p)}) = 0$
. We henceforth disregard the primes q that are of nonsplit multiplicative and additive reduction type. For the same reason, we may also disregard (for the purpose of proportion) the primes of split multiplicative reduction. As
$\mathfrak {d}(\mathcal {N}_{(E,p)}) = 0$
. We henceforth disregard the primes q that are of nonsplit multiplicative and additive reduction type. For the same reason, we may also disregard (for the purpose of proportion) the primes of split multiplicative reduction. As
![]() $X\rightarrow \infty $
, the contribution to
$X\rightarrow \infty $
, the contribution to
![]() $\mathcal {E}_{(E,p)}$
is primarily from primes q such that:
$\mathcal {E}_{(E,p)}$
is primarily from primes q such that:
-
(a) q is a prime of good ordinary reduction;
-
(b)
 $q\equiv 1\ \pmod {\,p}$
; and
$q\equiv 1\ \pmod {\,p}$
; and -
(c)
 $p\mid \# \widetilde {E}({\mathbb F}_q)$
.
$p\mid \# \widetilde {E}({\mathbb F}_q)$
.
For non-CM elliptic curves, the set of primes of good ordinary reduction has density
![]() $1$
. In the case of non-CM elliptic curves with surjective residual Galois representation at p, we know how to calculate the proportion of primes satisfying conditions (a)–(c).
$1$
. In the case of non-CM elliptic curves with surjective residual Galois representation at p, we know how to calculate the proportion of primes satisfying conditions (a)–(c).
Lemma 3.9. Let
![]() $E_{/{\mathbb Q}}$
be a non-CM elliptic curve and
$E_{/{\mathbb Q}}$
be a non-CM elliptic curve and
![]() $p\geq 5$
be a fixed prime of good ordinary reduction such that the residual Galois representation at p is surjective. Then,
$p\geq 5$
be a fixed prime of good ordinary reduction such that the residual Galois representation at p is surjective. Then,
Proof. The result is well known and follows from the proof of [Reference Garcia-Fritz and PastenGFP20, Proposition 4.6]. For the convenience of the reader, we briefly sketch the details here. A more detailed argument is provided in Section 4.2. Since
![]() $p\geq 5$
, it follows from the proof of Lemma 3.8 that if conditions (b) and (c) are satisfied, then condition (a) is automatically satisfied for any prime q of good reduction. Since there are only finitely many primes q at which E has bad reduction, we may as well assume that q is a prime of good reduction.
$p\geq 5$
, it follows from the proof of Lemma 3.8 that if conditions (b) and (c) are satisfied, then condition (a) is automatically satisfied for any prime q of good reduction. Since there are only finitely many primes q at which E has bad reduction, we may as well assume that q is a prime of good reduction.
Let
![]() $\operatorname {\mathrm {Frob}}_q$
denote the Frobenius at q and set
$\operatorname {\mathrm {Frob}}_q$
denote the Frobenius at q and set
![]() $\mathcal {S}$
to be the set of matrices
$\mathcal {S}$
to be the set of matrices
![]() $A\in \operatorname {\mathrm {GL}}_2({\mathbb F}_p)$
such that
$A\in \operatorname {\mathrm {GL}}_2({\mathbb F}_p)$
such that
![]() $\operatorname {\mathrm {trace}}(A)=2$
and
$\operatorname {\mathrm {trace}}(A)=2$
and
![]() $\det (A)=1$
. Let
$\det (A)=1$
. Let
![]() $\bar {\rho }:\operatorname {\mathrm {Gal}}(\bar {{\mathbb Q}}/{\mathbb Q})\rightarrow \operatorname {\mathrm {GL}}_2({\mathbb F}_p)$
denote the residual representation at p, that is, the representation on the group of p-torsion points
$\bar {\rho }:\operatorname {\mathrm {Gal}}(\bar {{\mathbb Q}}/{\mathbb Q})\rightarrow \operatorname {\mathrm {GL}}_2({\mathbb F}_p)$
denote the residual representation at p, that is, the representation on the group of p-torsion points
![]() $E[p]$
. By assumption,
$E[p]$
. By assumption,
![]() $\bar {\rho }$
is surjective.
$\bar {\rho }$
is surjective.
Since q is a prime of good reduction,
![]() $\bar {\rho }$
is unramified at q and the characteristic polynomial of
$\bar {\rho }$
is unramified at q and the characteristic polynomial of
![]() $\bar {\rho }(\operatorname {\mathrm {Frob}}_q)$
is given by
$\bar {\rho }(\operatorname {\mathrm {Frob}}_q)$
is given by
Thus, q satisfies both conditions (b) and (c) above if and only if
![]() $\bar {\rho }(\operatorname {\mathrm {Frob}}_q)$
is contained in
$\bar {\rho }(\operatorname {\mathrm {Frob}}_q)$
is contained in
![]() $\mathcal {S}$
. According to Lemma 4.8, the cardinality of
$\mathcal {S}$
. According to Lemma 4.8, the cardinality of
![]() $\mathcal {S}$
is
$\mathcal {S}$
is
![]() $p^2$
. The cardinality of
$p^2$
. The cardinality of
![]() $\operatorname {\mathrm {Image}}(\bar {\rho })=\operatorname {\mathrm {GL}}_2({\mathbb F}_p)$
is
$\operatorname {\mathrm {Image}}(\bar {\rho })=\operatorname {\mathrm {GL}}_2({\mathbb F}_p)$
is
![]() $(p^2-1)(p^2-p)$
. The result follows from the Chebotarev density theorem, according to which the density of
$(p^2-1)(p^2-p)$
. The result follows from the Chebotarev density theorem, according to which the density of
![]() $\mathcal {E}_{(E,p)}$
is
$\mathcal {E}_{(E,p)}$
is
 $$ \begin{align*}\frac{\#\mathcal{S}}{\# \operatorname{\mathrm{GL}}_2({\mathbb F}_q)}=\frac{p}{(p-1)^2(p+1)}.\\[-42pt] \end{align*} $$
$$ \begin{align*}\frac{\#\mathcal{S}}{\# \operatorname{\mathrm{GL}}_2({\mathbb F}_q)}=\frac{p}{(p-1)^2(p+1)}.\\[-42pt] \end{align*} $$
We performed calculations using SageMath [Sag20] to get an estimate of the proportion of enemy primes in the CM case. More precisely, fix
![]() $5 \leq p\leq 50$
. Fix an elliptic curve
$5 \leq p\leq 50$
. Fix an elliptic curve
![]() $E_{/{\mathbb Q}}$
of rank 0 and conductor less than 100. Running through all primes q less than 200 million, we computed the proportion of enemy primes. The results are recorded at the end of the article, in Table 2. The data suggest that for elliptic curves with CM, the proportion of enemy primes is half of that in the non-CM case. We know from Deuring’s criterion that for a CM elliptic curve, the density of the set of good ordinary primes is
$E_{/{\mathbb Q}}$
of rank 0 and conductor less than 100. Running through all primes q less than 200 million, we computed the proportion of enemy primes. The results are recorded at the end of the article, in Table 2. The data suggest that for elliptic curves with CM, the proportion of enemy primes is half of that in the non-CM case. We know from Deuring’s criterion that for a CM elliptic curve, the density of the set of good ordinary primes is
![]() $1/2$
. It therefore seems reasonable to assume that the enemy primes are equally likely to be primes of good ordinary or good supersingular reduction. More precisely, we make the following assumption.
$1/2$
. It therefore seems reasonable to assume that the enemy primes are equally likely to be primes of good ordinary or good supersingular reduction. More precisely, we make the following assumption.
Table 1 Values for Equation (3-4).

Table 2 Proportion of enemy primes.

Hypothesis 3.10. Let
![]() $E_{/{\mathbb Q}}$
be an elliptic curve with CM and p be a fixed odd prime of good ordinary reduction. Then,
$E_{/{\mathbb Q}}$
be an elliptic curve with CM and p be a fixed odd prime of good ordinary reduction. Then,
![]() $\mathfrak {d}({\mathcal E}_{(E,p)})= {p}/{2(p-1)^2(p+1)}$
.
$\mathfrak {d}({\mathcal E}_{(E,p)})= {p}/{2(p-1)^2(p+1)}$
.
We can now prove the main result of this section.
Theorem 3.11. Let
![]() $(E,p)$
be a given pair of a rank 0 elliptic curve over
$(E,p)$
be a given pair of a rank 0 elliptic curve over
![]() ${\mathbb Q}$
and a relevant prime
${\mathbb Q}$
and a relevant prime
![]() $p\geq 5$
. Then, the following assertions hold.
$p\geq 5$
. Then, the following assertions hold.
-
(1) Suppose that the residual representation at p is surjective. Then, there are infinitely many cyclic number fields of degree-p in which the
 $\lambda $
-invariant does not jump. In particular, there are infinitely many
$\lambda $
-invariant does not jump. In particular, there are infinitely many
 ${\mathbb Z}/p{\mathbb Z}$
-extensions
${\mathbb Z}/p{\mathbb Z}$
-extensions
 $L/{\mathbb Q}$
in which the rank does not jump in
$L/{\mathbb Q}$
in which the rank does not jump in
 $L_n$
for all
$L_n$
for all
 $n\geq 0$
.
$n\geq 0$
. -
(2) Let
 $(E,p)$
be a pair of a rank 0 elliptic curve (defined over
$(E,p)$
be a pair of a rank 0 elliptic curve (defined over
 ${\mathbb Q}$
) with complex multiplication and a relevant prime
${\mathbb Q}$
) with complex multiplication and a relevant prime
 $p \geq 5$
. Suppose further that Hypothesis 3.10 holds. Then the same conclusions hold as in the non-CM case.
$p \geq 5$
. Suppose further that Hypothesis 3.10 holds. Then the same conclusions hold as in the non-CM case.
Proof. Since p is assumed to be a relevant prime, we know that
![]() $\mu _p(E/{\mathbb Q})=\lambda _p(E/{\mathbb Q})=0$
. It follows from Theorem 2.3 that
$\mu _p(E/{\mathbb Q})=\lambda _p(E/{\mathbb Q})=0$
. It follows from Theorem 2.3 that
![]() $\mu _p(E/L)=0$
for every degree p extension
$\mu _p(E/L)=0$
for every degree p extension
![]() $L/{\mathbb Q}$
. The result will follow from Proposition 3.2 if we can show that there are infinitely many cyclic degree p extensions such that Equation (3-1) holds.
$L/{\mathbb Q}$
. The result will follow from Proposition 3.2 if we can show that there are infinitely many cyclic degree p extensions such that Equation (3-1) holds.
Observe that
 $$ \begin{align*} \mathfrak{d}({\mathcal F}_{(E,p)}) = \dfrac{1}{p-1} - \mathfrak{d}({\mathcal E}_{(E,p)}) = \begin{cases} \dfrac{p^2-p-1}{(p-1)^2(p+1)} & \text{if }E\text{ does not have CM,}\\[8pt] \dfrac{2p^2-p-2}{2(p-1)^2(p+1)} & \text{if }E\text{ does not have CM.} \end{cases} \end{align*} $$
$$ \begin{align*} \mathfrak{d}({\mathcal F}_{(E,p)}) = \dfrac{1}{p-1} - \mathfrak{d}({\mathcal E}_{(E,p)}) = \begin{cases} \dfrac{p^2-p-1}{(p-1)^2(p+1)} & \text{if }E\text{ does not have CM,}\\[8pt] \dfrac{2p^2-p-2}{2(p-1)^2(p+1)} & \text{if }E\text{ does not have CM.} \end{cases} \end{align*} $$
It follows from Lemma 3.7 that Equation (3-1) holds when every ramified prime is a friendly prime. From the above discussion, we see that there are infinitely many friendly primes. We have also shown in Proposition 3.4 that corresponding to each friendly prime (say q), there is one
![]() ${\mathbb Z}/p{\mathbb Z}$
-extension where only q ramifies. This completes the proof.
${\mathbb Z}/p{\mathbb Z}$
-extension where only q ramifies. This completes the proof.
Note that condition (1) in Theorem 3.11, requiring that the residual representation is surjective, implies that the elliptic curve does not have complex multiplication. The Galois representations associated to CM elliptic curves are studied, for instance, in [Reference Lozano-RobledoLR22]. The following application of our theorem was pointed out by J. Morrow. We begin by stating a result of González-Jiménez and Najman.
Theorem 3.12. Let
![]() $E_{/{\mathbb Q}}$
be an elliptic curve and
$E_{/{\mathbb Q}}$
be an elliptic curve and
![]() $p>7$
be a prime number. Let
$p>7$
be a prime number. Let
![]() $L/{\mathbb Q}$
be a Galois extension with Galois group
$L/{\mathbb Q}$
be a Galois extension with Galois group
![]() $G\simeq {\mathbb Z}/p{\mathbb Z}$
. Then,
$G\simeq {\mathbb Z}/p{\mathbb Z}$
. Then,
![]() $E(L)_{\operatorname {\mathrm {tors}}}=E({\mathbb Q})_{\operatorname {\mathrm {tors}}}$
.
$E(L)_{\operatorname {\mathrm {tors}}}=E({\mathbb Q})_{\operatorname {\mathrm {tors}}}$
.
Proof. See [Reference González-Jiménez and NajmanGJN20, Theorem 7.2].
Combining Theorems 3.11 and 3.12, the following corollary is immediate.
Corollary 3.13. Let
![]() $(E,p)$
be a given pair of a rank 0 elliptic curve over
$(E,p)$
be a given pair of a rank 0 elliptic curve over
![]() ${\mathbb Q}$
and a relevant prime
${\mathbb Q}$
and a relevant prime
![]() $p> 7$
. If
$p> 7$
. If
![]() $E_{/{\mathbb Q}}$
is an elliptic curve without CM, suppose that the residual representation at p is surjective. If
$E_{/{\mathbb Q}}$
is an elliptic curve without CM, suppose that the residual representation at p is surjective. If
![]() $E_{/{\mathbb Q}}$
is an elliptic curve with CM, suppose that Hypothesis 3.10 holds. Then, there are infinitely many
$E_{/{\mathbb Q}}$
is an elliptic curve with CM, suppose that Hypothesis 3.10 holds. Then, there are infinitely many
![]() ${\mathbb Z}/p{\mathbb Z}$
-extensions of
${\mathbb Z}/p{\mathbb Z}$
-extensions of
![]() ${\mathbb Q}$
where the Mordell–Weil group does not grow.
${\mathbb Q}$
where the Mordell–Weil group does not grow.
Remark 3.14. To show that there are ‘infinitely many’
![]() ${\mathbb Z}/p{\mathbb Z}$
-extensions with no
${\mathbb Z}/p{\mathbb Z}$
-extensions with no
![]() $\lambda $
-jump, we only counted those where exactly one friendly prime is ramified. In particular, we counted only those
$\lambda $
-jump, we only counted those where exactly one friendly prime is ramified. In particular, we counted only those
![]() ${\mathbb Z}/p{\mathbb Z}$
-extensions that are contained in the cyclotomic field
${\mathbb Z}/p{\mathbb Z}$
-extensions that are contained in the cyclotomic field
![]() ${\mathbb Q}(\mu _q)$
where q is a prime of the form
${\mathbb Q}(\mu _q)$
where q is a prime of the form
![]() $1 \ \pmod {\,p}$
. Our count ignored the contribution from
$1 \ \pmod {\,p}$
. Our count ignored the contribution from
![]() ${\mathbb Z}/p{\mathbb Z}$
-extensions where two or more primes are ramified, all of which are either friendly primes or the prime p. It was pointed out to us by R. Lemke Oliver that Theorem 3.11 can be made explicit using standard analytic number theory techniques (see for example [Reference SerreSer74, Théorème 2.4]); however, our approach is still likely to fall short of proving a positive proportion.
${\mathbb Z}/p{\mathbb Z}$
-extensions where two or more primes are ramified, all of which are either friendly primes or the prime p. It was pointed out to us by R. Lemke Oliver that Theorem 3.11 can be made explicit using standard analytic number theory techniques (see for example [Reference SerreSer74, Théorème 2.4]); however, our approach is still likely to fall short of proving a positive proportion.
A recent and significant result in this direction is by Mazur and Rubin (see [Reference Mazur, Rubin and LarsenMRL18, Theorem 1.2]). They show that given an elliptic curve E, there is a positive density set of primes (call it
![]() $\mathcal {S}$
) such that for each
$\mathcal {S}$
) such that for each
![]() $p\in \mathcal {S}$
, there are infinitely many
$p\in \mathcal {S}$
, there are infinitely many
![]() ${\mathbb Z}/p{\mathbb Z}$
-extensions over
${\mathbb Z}/p{\mathbb Z}$
-extensions over
![]() ${\mathbb Q}$
with
${\mathbb Q}$
with
![]() $E(L) = E({\mathbb Q})$
. In the case of rank 0 elliptic curves (defined over
$E(L) = E({\mathbb Q})$
. In the case of rank 0 elliptic curves (defined over
![]() ${\mathbb Q}$
), our result is stronger, in the sense that for
${\mathbb Q}$
), our result is stronger, in the sense that for
![]() $p>7$
, Corollary 3.13 holds unconditionally for density 1 primes if E is an elliptic curve without CM. However, for CM elliptic curves, the result is conditional and applies to a set of primes of density
$p>7$
, Corollary 3.13 holds unconditionally for density 1 primes if E is an elliptic curve without CM. However, for CM elliptic curves, the result is conditional and applies to a set of primes of density
![]() $1/2$
.
$1/2$
.
3.1.2 Example: CM case
Now, we work out a particular example in the CM case. As before, let
![]() $p\geq 5$
be a fixed prime and
$p\geq 5$
be a fixed prime and
![]() $q\equiv 1 \ \pmod {\,p}$
be a different prime. Let
$q\equiv 1 \ \pmod {\,p}$
be a different prime. Let
![]() $k\not \equiv 0 \ \pmod {\,q}$
and consider the family of curves
$k\not \equiv 0 \ \pmod {\,q}$
and consider the family of curves
Then, either of the following two statements is true (see [Reference WashingtonWas08, Section 4.4]).
-
(i) If
 $q\equiv 3 \ \pmod {\,4}$
, then
$q\equiv 3 \ \pmod {\,4}$
, then
 $\# \widetilde {E_k}(\mathbb {F}_q) = q +1$
.
$\# \widetilde {E_k}(\mathbb {F}_q) = q +1$
. -
(ii) If
 $q\equiv 1 \ \pmod {\,4}$
, write
$q\equiv 1 \ \pmod {\,4}$
, write
 $q= s^2 + t^2$
with
$q= s^2 + t^2$
with
 $s\in {\mathbb Z}$
,
$s\in {\mathbb Z}$
,
 $t\in 2{\mathbb Z}$
and
$t\in 2{\mathbb Z}$
and
 $s+t \equiv 1 \ \pmod {\,4}$
. Then,
$s+t \equiv 1 \ \pmod {\,4}$
. Then,  $$ \begin{align*} \# \widetilde{E_k}(\mathbb{F}_q) = \begin{cases} q + 1 - 2s & \textrm{if } k \textrm{ is a fourth power mod }q,\\ q + 1 + 2s & \textrm{if } k \textrm{ is a square mod }q \textrm{ but not a fourth power},\\ q + 1 \pm 2t & \textrm{if } k \textrm{ is not a square mod }q. \end{cases} \end{align*} $$
$$ \begin{align*} \# \widetilde{E_k}(\mathbb{F}_q) = \begin{cases} q + 1 - 2s & \textrm{if } k \textrm{ is a fourth power mod }q,\\ q + 1 + 2s & \textrm{if } k \textrm{ is a square mod }q \textrm{ but not a fourth power},\\ q + 1 \pm 2t & \textrm{if } k \textrm{ is not a square mod }q. \end{cases} \end{align*} $$
For this family of elliptic curves, the primes
![]() $q\equiv 3 \ \pmod {\,4}$
are supersingular. Recall from Lemma 3.8 that if q is a supersingular prime and
$q\equiv 3 \ \pmod {\,4}$
are supersingular. Recall from Lemma 3.8 that if q is a supersingular prime and
![]() $q\equiv 1 \ \pmod {\,p}$
, then the primes
$q\equiv 1 \ \pmod {\,p}$
, then the primes
![]() $w|q$
are friendly (except for possibly finitely many). For the sake of concreteness, suppose that
$w|q$
are friendly (except for possibly finitely many). For the sake of concreteness, suppose that
![]() $k=1$
(the argument goes through more generally). By the Chinese remainder theorem, we know that if
$k=1$
(the argument goes through more generally). By the Chinese remainder theorem, we know that if
 $$ \begin{align*} q&\equiv 3 \ \pmod{\,4} \textrm{ and }\\ q&\equiv 1 \ \pmod{\,p}, \end{align*} $$
$$ \begin{align*} q&\equiv 3 \ \pmod{\,4} \textrm{ and }\\ q&\equiv 1 \ \pmod{\,p}, \end{align*} $$
then
![]() $q \equiv 2p+1 \ \pmod {\,4p}$
. By Dirichlet’s theorem for primes in arithmetic progressions, we know that there are infinitely many primes satisfying this congruence condition. Moreover, the proportion of such primes is
$q \equiv 2p+1 \ \pmod {\,4p}$
. By Dirichlet’s theorem for primes in arithmetic progressions, we know that there are infinitely many primes satisfying this congruence condition. Moreover, the proportion of such primes is
 $$ \begin{align*} \frac{1}{\varphi(4p)} = \frac{1}{2(p-1)}. \end{align*} $$
$$ \begin{align*} \frac{1}{\varphi(4p)} = \frac{1}{2(p-1)}. \end{align*} $$
By Proposition 3.4, we know that corresponding to each such q, there is exactly one cyclic degree-p extension
![]() $L/{\mathbb Q}$
in which q is the unique ramified prime. Therefore, we have produced infinitely many
$L/{\mathbb Q}$
in which q is the unique ramified prime. Therefore, we have produced infinitely many
![]() ${\mathbb Z}/p{\mathbb Z}$
-extensions where the ramified primes are friendly. By Proposition 3.2, if
${\mathbb Z}/p{\mathbb Z}$
-extensions where the ramified primes are friendly. By Proposition 3.2, if
![]() $\operatorname {\mathrm {rank}}_{{\mathbb Z}}(E_k/{\mathbb Q}) =0$
and
$\operatorname {\mathrm {rank}}_{{\mathbb Z}}(E_k/{\mathbb Q}) =0$
and
![]() $\mu _p(E/{\mathbb Q})=0$
(for example, when
$\mu _p(E/{\mathbb Q})=0$
(for example, when
![]() $k=1$
), then there are infinitely many
$k=1$
), then there are infinitely many
![]() ${\mathbb Z}/p{\mathbb Z}$
-extensions over
${\mathbb Z}/p{\mathbb Z}$
-extensions over
![]() ${\mathbb Q}$
where the rank does not jump.
${\mathbb Q}$
where the rank does not jump.
We record a specific case of the above discussion.
Theorem 3.15. Let
![]() $p\geq 5$
be a fixed prime, and consider the elliptic curve
$p\geq 5$
be a fixed prime, and consider the elliptic curve
Then, there are infinitely many
![]() ${\mathbb Z}/p{\mathbb Z}$
-extensions
${\mathbb Z}/p{\mathbb Z}$
-extensions
![]() $L/{\mathbb Q}$
such that
$L/{\mathbb Q}$
such that
![]() $\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/L_{\operatorname {\mathrm {cyc}}})=0$
. In particular, there are infinitely many
$\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/L_{\operatorname {\mathrm {cyc}}})=0$
. In particular, there are infinitely many
![]() ${\mathbb Z}/p{\mathbb Z}$
-extensions such that
${\mathbb Z}/p{\mathbb Z}$
-extensions such that
![]() $\operatorname {\mathrm {rank}}_{{\mathbb Z}}(E(L))=0$
.
$\operatorname {\mathrm {rank}}_{{\mathbb Z}}(E(L))=0$
.
3.2
In the last section, we fixed a rank 0 elliptic curve over
![]() ${\mathbb Q}$
and analyzed in how many
${\mathbb Q}$
and analyzed in how many
![]() ${\mathbb Z}/p{\mathbb Z}$
-extensions of
${\mathbb Z}/p{\mathbb Z}$
-extensions of
![]() ${\mathbb Q}$
did the rank jump. Now, we ask the following question.
${\mathbb Q}$
did the rank jump. Now, we ask the following question.
Question 3.16. Let
![]() $p\geq 5$
be a fixed odd prime. For what proportion of rank 0 elliptic curves does there exist at least one degree-p Galois extension over
$p\geq 5$
be a fixed odd prime. For what proportion of rank 0 elliptic curves does there exist at least one degree-p Galois extension over
![]() ${\mathbb Q}$
disjoint from
${\mathbb Q}$
disjoint from
![]() ${\mathbb Q}_{\operatorname {\mathrm {cyc}}}$
such that its rank remains 0 upon base-change?
${\mathbb Q}_{\operatorname {\mathrm {cyc}}}$
such that its rank remains 0 upon base-change?
Let E be a rank 0 elliptic curve of conductor N and p be a relevant prime. Throughout this section, we assume that the Shafarevich–Tate group of rank 0 elliptic curves defined over
![]() ${\mathbb Q}$
is finite. Proposition 2.5 asserts that density one good ordinary primes are relevant. Further assume that N is divisible by at least one prime of the form
${\mathbb Q}$
is finite. Proposition 2.5 asserts that density one good ordinary primes are relevant. Further assume that N is divisible by at least one prime of the form
![]() $1\ \pmod {\,p}$
. The following lemma is a special case of Proposition 3.2.
$1\ \pmod {\,p}$
. The following lemma is a special case of Proposition 3.2.
Lemma 3.17. Keep the setting as above. If E has no prime of split multiplicative reduction, that is,
![]() $P_1 = \emptyset $
, then there exists at least one degree-p cyclic extension
$P_1 = \emptyset $
, then there exists at least one degree-p cyclic extension
![]() $L/{\mathbb Q}$
such that
$L/{\mathbb Q}$
such that
![]() $\lambda _p(E/L)=0$
. In particular,
$\lambda _p(E/L)=0$
. In particular,
![]() $\operatorname {\mathrm {rank}}_{{\mathbb Z}}(E(L))=0$
.
$\operatorname {\mathrm {rank}}_{{\mathbb Z}}(E(L))=0$
.
Proof. By Proposition 3.4, there exists one and only one cyclic degree-p extension
![]() $L/{\mathbb Q}$
of conductor q if and only if
$L/{\mathbb Q}$
of conductor q if and only if
![]() $q\equiv 1 \ \pmod {\,p}$
. By assumption, N has a prime divisor of this form (say
$q\equiv 1 \ \pmod {\,p}$
. By assumption, N has a prime divisor of this form (say
![]() $q_0$
). Let
$q_0$
). Let
![]() $L/{\mathbb Q}$
be the
$L/{\mathbb Q}$
be the
![]() ${\mathbb Z}/p{\mathbb Z}$
-extension of conductor
${\mathbb Z}/p{\mathbb Z}$
-extension of conductor
![]() $q_0$
. Moreover, there is no contribution from the last term of the formula in Theorem 2.3; indeed, for any
$q_0$
. Moreover, there is no contribution from the last term of the formula in Theorem 2.3; indeed, for any
![]() $w\in P_2$
, the ramification index is
$w\in P_2$
, the ramification index is
![]() $e_{L/{\mathbb Q}}(w)=1$
. Since L is a
$e_{L/{\mathbb Q}}(w)=1$
. Since L is a
![]() ${\mathbb Z}/p{\mathbb Z}$
-extension, it follows from Theorem 2.3 that
${\mathbb Z}/p{\mathbb Z}$
-extension, it follows from Theorem 2.3 that
![]() $\mu _p(E/L)=0$
. In this
$\mu _p(E/L)=0$
. In this
![]() ${\mathbb Z}/p{\mathbb Z}$
-extension, we have forced
${\mathbb Z}/p{\mathbb Z}$
-extension, we have forced
![]() $\lambda _p(E/L)=0$
. Therefore,
$\lambda _p(E/L)=0$
. Therefore,
![]() $\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/L_{\operatorname {\mathrm {cyc}}})=0$
. Clearly,
$\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/L_{\operatorname {\mathrm {cyc}}})=0$
. Clearly,
![]() $\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/L)$
is trivial as well; this forces
$\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/L)$
is trivial as well; this forces
![]() $\operatorname {\mathrm {rank}}_{{\mathbb Z}}(E(L))=0$
.
$\operatorname {\mathrm {rank}}_{{\mathbb Z}}(E(L))=0$
.
It follows from the proof of the above result that to obtain a lower bound of the proportion of rank 0 elliptic curves for which there is at least one degree-p cyclic extension over
![]() ${\mathbb Q}$
such that
${\mathbb Q}$
such that
![]() $\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/L)=0$
, it is enough to count elliptic curves with the following properties:
$\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/L)=0$
, it is enough to count elliptic curves with the following properties:
-
(i) E has good ordinary reduction at
 $p\geq 5$
;
$p\geq 5$
; -
(ii) E has any reduction type at primes
 $q\not \equiv 1 \ \pmod {\,p}$
;
$q\not \equiv 1 \ \pmod {\,p}$
; -
(iii) E has at least one prime of bad reduction that is not of split multiplicative type at a prime
 $q\equiv 1\ \pmod {\,p}$
.
$q\equiv 1\ \pmod {\,p}$
.
Before proceeding with such a count, we need to define the notion of height. For an elliptic curve defined over
![]() ${\mathbb Q}$
, consider the long Weierstrass equation:
${\mathbb Q}$
, consider the long Weierstrass equation:
Define the height of this Weierstrass equation with integer coefficients
![]() $\boldsymbol {a}=(a_1, a_2, a_3, a_4, a_6)$
to be
$\boldsymbol {a}=(a_1, a_2, a_3, a_4, a_6)$
to be
Let S be a set of Weierstrass equations with integer coefficients
![]() $\boldsymbol {a}$
that are ordered by height. The proportion of Weierstrass equations that lie in the set S is defined as
$\boldsymbol {a}$
that are ordered by height. The proportion of Weierstrass equations that lie in the set S is defined as
 $$ \begin{align} \lim_{X\rightarrow \infty}\frac{\#\{ \boldsymbol{a}\in S : \operatorname{\mathrm{height}}(\boldsymbol{a}) <X\}}{\#\{ \boldsymbol{a}\in {\mathbb Z}^5 : \operatorname{\mathrm{height}}(\boldsymbol{a}) <X\}}. \end{align} $$
$$ \begin{align} \lim_{X\rightarrow \infty}\frac{\#\{ \boldsymbol{a}\in S : \operatorname{\mathrm{height}}(\boldsymbol{a}) <X\}}{\#\{ \boldsymbol{a}\in {\mathbb Z}^5 : \operatorname{\mathrm{height}}(\boldsymbol{a}) <X\}}. \end{align} $$
For our purposes, we restrict to Weierstrass equations that are globally minimal.
Lemma 3.18. Let q be any prime. Suppose that all elliptic curves defined over
![]() ${\mathbb Q}$
are ordered by height. Then:
${\mathbb Q}$
are ordered by height. Then:
-
(i) the proportion with split multiplicative reduction at q is
 $ ({q-1})/{2q^2}$
;
$ ({q-1})/{2q^2}$
; -
(ii) the proportion with good reduction at q is
 $(1 - {1}/{q})$
.
$(1 - {1}/{q})$
.
Proof. For part (i), see [Reference Cremona and SadekCS21, Theorem 5.1]. For part (ii), see [Reference Cremona and SadekCS21, Proposition 2.2].
Henceforth, we assume that the rank of the elliptic curve and the reduction type at
![]() $\ell $
are independent of each other. In other words, we assume that even if we only order the rank 0 elliptic curves by height, the proportion of elliptic curves with split multiplicative reduction or good reduction is the same as that in Lemma 3.18.
$\ell $
are independent of each other. In other words, we assume that even if we only order the rank 0 elliptic curves by height, the proportion of elliptic curves with split multiplicative reduction or good reduction is the same as that in Lemma 3.18.
We know from [Reference Cremona and SadekCS21, Section 3] that the local conditions such as the reduction type of elliptic curves at distinct primes are independent.
We now record the assumption we have made.
Hypothesis 3.19. The reduction type of an elliptic curve at a prime q is independent of its rank.
What we mean is that density results from Lemma 3.18 hold even when we restrict to rank 0 elliptic curves defined over
![]() ${\mathbb Q}$
. We can now prove the main result in this section.
${\mathbb Q}$
. We can now prove the main result in this section.
Theorem 3.20. Let
![]() $p\geq 5$
be a fixed odd prime. Suppose that Hypothesis 3.19 holds. Varying over all rank 0 elliptic curves defined over
$p\geq 5$
be a fixed odd prime. Suppose that Hypothesis 3.19 holds. Varying over all rank 0 elliptic curves defined over
![]() ${\mathbb Q}$
and ordered by height, the proportion with
${\mathbb Q}$
and ordered by height, the proportion with
-
(i) good reduction at p;
-
(ii) any reduction type at
 $q\not \equiv 1 \ \pmod {\,p}$
; and
$q\not \equiv 1 \ \pmod {\,p}$
; and -
(iii) at least one prime of bad reduction where the reduction type is not split multiplicative at a prime
 $q\equiv 1\ \pmod {\,p}$
is given by
$q\equiv 1\ \pmod {\,p}$
is given by
 $$ \begin{align} \bigg(1 - \frac{1}{p} \bigg) \bigg( 1 - \prod_{q \equiv 1 \ \pmod{\,p}} \bigg( \frac{q-1}{2q^2} + 1 - \frac{1}{q}\bigg) \bigg). \end{align} $$
$$ \begin{align} \bigg(1 - \frac{1}{p} \bigg) \bigg( 1 - \prod_{q \equiv 1 \ \pmod{\,p}} \bigg( \frac{q-1}{2q^2} + 1 - \frac{1}{q}\bigg) \bigg). \end{align} $$
Further, suppose that the Shafarevich–Tate group is finite for all rank 0 elliptic curves defined over
![]() ${\mathbb Q}$
. There is a positive proportion of rank 0 elliptic curves for which there is at least one degree-p cyclic extension over
${\mathbb Q}$
. There is a positive proportion of rank 0 elliptic curves for which there is at least one degree-p cyclic extension over
![]() ${\mathbb Q}$
such that
${\mathbb Q}$
such that
![]() $\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/L)=0$
upon base-change.
$\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/L)=0$
upon base-change.
Proof. Let
![]() $q \equiv 1\ \pmod {\,p}$
. We require that among all such primes, there is ‘at least one prime of bad reduction where the reduction type is not split multiplicative’. Equivalently, among all primes of the form
$q \equiv 1\ \pmod {\,p}$
. We require that among all such primes, there is ‘at least one prime of bad reduction where the reduction type is not split multiplicative’. Equivalently, among all primes of the form
![]() $1\ \pmod {\,p}$
, there is ‘at least one prime of additive or nonsplit multiplicative reduction’. In other words, at
$1\ \pmod {\,p}$
, there is ‘at least one prime of additive or nonsplit multiplicative reduction’. In other words, at
![]() $q\equiv 1 \ \pmod {\,p}$
, we want the negation of ‘all primes have either good or split multiplicative reduction’. This gives Equation (3-4) from Lemma 3.18.
$q\equiv 1 \ \pmod {\,p}$
, we want the negation of ‘all primes have either good or split multiplicative reduction’. This gives Equation (3-4) from Lemma 3.18.
From our earlier discussion, to prove the second assertion, it remains to show that Equation (3-4) is strictly positive. For any fixed prime p, note that
 $$ \begin{align*} \prod_{q \equiv 1 (\textrm{mod }{p})} \bigg( \frac{q-1}{2q^2} + 1 - \frac{1}{q}\bigg) = \prod_{q \equiv 1 (\textrm{mod }{p})} \bigg( 1 - \bigg(\frac{q+1}{2q^2}\bigg)\bigg)< 1. \end{align*} $$
$$ \begin{align*} \prod_{q \equiv 1 (\textrm{mod }{p})} \bigg( \frac{q-1}{2q^2} + 1 - \frac{1}{q}\bigg) = \prod_{q \equiv 1 (\textrm{mod }{p})} \bigg( 1 - \bigg(\frac{q+1}{2q^2}\bigg)\bigg)< 1. \end{align*} $$
The inequality follows from the fact that each term in the product is
![]() $<1$
. Therefore,
$<1$
. Therefore,
 $$ \begin{align*} \bigg( 1 - \prod_{q \equiv 1 (\textrm{mod }{p})} \bigg( 1 - \bigg(\frac{q+1}{2q^2}\bigg)\bigg)\bigg)>0. \end{align*} $$
$$ \begin{align*} \bigg( 1 - \prod_{q \equiv 1 (\textrm{mod }{p})} \bigg( 1 - \bigg(\frac{q+1}{2q^2}\bigg)\bigg)\bigg)>0. \end{align*} $$
The claim follows.
In Table 1, we compute Equation (3-4) for
![]() $3\leq p < 50$
and
$3\leq p < 50$
and
![]() $q \leq 179\,424\,673$
(that is, the first 10 million primes).
$q \leq 179\,424\,673$
(that is, the first 10 million primes).
A reasonable question to ask at this point is the following.
Question 3.21. Let
![]() $p\geq 5$
be a fixed prime and
$p\geq 5$
be a fixed prime and
![]() $L/{\mathbb Q}$
be a fixed
$L/{\mathbb Q}$
be a fixed
![]() ${\mathbb Z}/p{\mathbb Z}$
-extension. Varying over all rank 0 elliptic curves over
${\mathbb Z}/p{\mathbb Z}$
-extension. Varying over all rank 0 elliptic curves over
![]() ${\mathbb Q}$
ordered by height, for what proportion is
${\mathbb Q}$
ordered by height, for what proportion is
![]() $\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/L_{\operatorname {\mathrm {cyc}}})=0$
?
$\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/L_{\operatorname {\mathrm {cyc}}})=0$
?
In this direction, we can provide partial answers. Given a number field
![]() $L/{\mathbb Q}$
, we can find a lower bound for the proportion of elliptic curves (defined over
$L/{\mathbb Q}$
, we can find a lower bound for the proportion of elliptic curves (defined over
![]() ${\mathbb Q}$
) for which Equation (3-1) holds.
${\mathbb Q}$
) for which Equation (3-1) holds.
Proposition 3.22. Let p be a fixed odd prime. Let
![]() $L/{\mathbb Q}$
be a fixed
$L/{\mathbb Q}$
be a fixed
![]() ${\mathbb Z}/p{\mathbb Z}$
-extension that is tamely ramified at primes
${\mathbb Z}/p{\mathbb Z}$
-extension that is tamely ramified at primes
![]() $q_1, \ldots , q_r$
. The proportion of elliptic curves defined over
$q_1, \ldots , q_r$
. The proportion of elliptic curves defined over
![]() ${\mathbb Q}$
(ordered by height) such that Equation (3-1) holds has a lower bound of
${\mathbb Q}$
(ordered by height) such that Equation (3-1) holds has a lower bound of
 $$ \begin{align*} \prod_{q_i=1}^r \bigg( \frac{q_i+1}{2q_i^2}\bigg). \end{align*} $$
$$ \begin{align*} \prod_{q_i=1}^r \bigg( \frac{q_i+1}{2q_i^2}\bigg). \end{align*} $$
Proof. Note that for Equation (3-1) to hold, the reduction type at p does not matter. To find a lower bound, it suffices that all the ramified primes (that is, the
![]() $q_i$
terms) are primes of bad reduction of nonsplit multiplicative or additive reduction type. Indeed, this would ensure
$q_i$
terms) are primes of bad reduction of nonsplit multiplicative or additive reduction type. Indeed, this would ensure
![]() $P_1 =\emptyset $
and the primes of good reduction are not ramified. Equivalently, each
$P_1 =\emptyset $
and the primes of good reduction are not ramified. Equivalently, each
![]() $q_i$
is such that it does not have good ordinary or split multiplicative reduction. By Lemma 3.18, the lower bound is
$q_i$
is such that it does not have good ordinary or split multiplicative reduction. By Lemma 3.18, the lower bound is
 $$ \begin{align*} \prod_{q_i=1}^r \bigg( 1 - \bigg(\frac{q_i -1}{2q_i^2} + 1 - \frac{1}{q_i}\bigg)\bigg) = \prod_{q_i=1}^r \bigg( \frac{q_i+1}{2q_i^2}\bigg).\\[-46pt] \end{align*} $$
$$ \begin{align*} \prod_{q_i=1}^r \bigg( 1 - \bigg(\frac{q_i -1}{2q_i^2} + 1 - \frac{1}{q_i}\bigg)\bigg) = \prod_{q_i=1}^r \bigg( \frac{q_i+1}{2q_i^2}\bigg).\\[-46pt] \end{align*} $$
Remark 3.23. The above proposition is not sufficient to answer the question because given p, we are unable to compute the proportion of elliptic curves for which p is relevant. In particular, we do not know precisely for what proportion of elliptic curves p is a good ordinary prime. A lower bound for this proportion has been computed for small primes and can be found in [Reference Kundu and RayKR21b, Table 1]. From the Hasse interval, one may conclude (roughly) that supersingular elliptic curves should be rare among elliptic curves with good reduction over
![]() $\mathbb {F}_p$
(approximately
$\mathbb {F}_p$
(approximately
![]() ${1}/{2\sqrt {p}}$
). Therefore, as p becomes large, 100% of the elliptic curves with good reduction at p is of ordinary type (see [Reference BirchBir68]). It is also reasonable to expect that as p becomes large, the proportion of rank 0 elliptic curves with
${1}/{2\sqrt {p}}$
). Therefore, as p becomes large, 100% of the elliptic curves with good reduction at p is of ordinary type (see [Reference BirchBir68]). It is also reasonable to expect that as p becomes large, the proportion of rank 0 elliptic curves with
![]() $\mu _p(E/{\mathbb Q})= \lambda _p(E/{\mathbb Q}) =0$
approaches 100% (see [Reference Kundu and RayKR21a, Conjecture 4.7]). Thus, assuming the rank distribution conjecture, it might be reasonable to expect that as p becomes large, varying over all elliptic curves ordered by height, the proportion with good ordinary reduction at p approaches
$\mu _p(E/{\mathbb Q})= \lambda _p(E/{\mathbb Q}) =0$
approaches 100% (see [Reference Kundu and RayKR21a, Conjecture 4.7]). Thus, assuming the rank distribution conjecture, it might be reasonable to expect that as p becomes large, varying over all elliptic curves ordered by height, the proportion with good ordinary reduction at p approaches
![]() $\tfrac 12 ( 1 - {1}/{2\sqrt {p}})( 1- {1}/{p})$
.
$\tfrac 12 ( 1 - {1}/{2\sqrt {p}})( 1- {1}/{p})$
.
4 Growth of the Selmer group of an elliptic curve in a
 ${\mathbb Z}/p{\mathbb Z}$
-extension
${\mathbb Z}/p{\mathbb Z}$
-extension
Throughout this section,
![]() $p\geq 5$
is a fixed prime number and
$p\geq 5$
is a fixed prime number and
![]() $E_{/{\mathbb Q}}$
an elliptic curve with good ordinary reduction at p for which the following equivalent conditions are satisfied:
$E_{/{\mathbb Q}}$
an elliptic curve with good ordinary reduction at p for which the following equivalent conditions are satisfied:
-
(i)
 $\mu _p(E/{\mathbb Q})=0$
and
$\mu _p(E/{\mathbb Q})=0$
and
 $\lambda _p(E/{\mathbb Q})=0$
;
$\lambda _p(E/{\mathbb Q})=0$
; -
(ii)
 $\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/{\mathbb Q}_{\operatorname {\mathrm {cyc}}})=0$
.
$\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/{\mathbb Q}_{\operatorname {\mathrm {cyc}}})=0$
.
Let L be a
![]() ${\mathbb Z}/p{\mathbb Z}$
-extension of
${\mathbb Z}/p{\mathbb Z}$
-extension of
![]() ${\mathbb Q}$
. First, in Proposition 4.1, we establish a criterion for there to be either a rank-jump or growth in the Shafarevich–Tate group. The result also explores conditions under which the Selmer groups
${\mathbb Q}$
. First, in Proposition 4.1, we establish a criterion for there to be either a rank-jump or growth in the Shafarevich–Tate group. The result also explores conditions under which the Selmer groups
This result is then applied to study a problem in arithmetic statistics which we prove in Theorem 4.9.
4.1
Here, we first prove a criterion for nontriviality of the p-primary Selmer group.
Proposition 4.1. Let p be an odd prime and
![]() $L/{\mathbb Q}$
be a
$L/{\mathbb Q}$
be a
![]() ${\mathbb Z}/p{\mathbb Z}$
-extension linearly disjoint from
${\mathbb Z}/p{\mathbb Z}$
-extension linearly disjoint from
![]() ${\mathbb Q}_{\operatorname {\mathrm {cyc}}}$
. In other words,
${\mathbb Q}_{\operatorname {\mathrm {cyc}}}$
. In other words,
![]() $L\neq {\mathbb Q}_1$
, where
$L\neq {\mathbb Q}_1$
, where
![]() ${\mathbb Q}_1$
is the first layer in the cyclotomic
${\mathbb Q}_1$
is the first layer in the cyclotomic
![]() ${\mathbb Z}_p$
-extension. Let
${\mathbb Z}_p$
-extension. Let
![]() $E_{/{\mathbb Q}}$
be an elliptic curve with good ordinary reduction at p and
$E_{/{\mathbb Q}}$
be an elliptic curve with good ordinary reduction at p and
![]() $\Sigma _L$
be the set of primes
$\Sigma _L$
be the set of primes
![]() $\ell \neq p$
that are ramified in L. Assume that the following conditions are satisfied:
$\ell \neq p$
that are ramified in L. Assume that the following conditions are satisfied:
-
(i)
 $\operatorname {\mathrm {rank}}_{{\mathbb Z}} E({\mathbb Q})=0$
and
$\operatorname {\mathrm {rank}}_{{\mathbb Z}} E({\mathbb Q})=0$
and
 $E({\mathbb Q})[p^{\infty }]=0$
;
$E({\mathbb Q})[p^{\infty }]=0$
; -
(ii)
 $\mu _p(E/{\mathbb Q})=0$
and
$\mu _p(E/{\mathbb Q})=0$
and
 $\lambda _p(E/{\mathbb Q})=0$
;
$\lambda _p(E/{\mathbb Q})=0$
; -
(iii) there is a prime
 $\ell \in \Sigma _L$
at which E has good reduction and
$\ell \in \Sigma _L$
at which E has good reduction and
 $p|\#\widetilde {E}({\mathbb F}_{\ell })$
;
$p|\#\widetilde {E}({\mathbb F}_{\ell })$
; -
(iv) at each prime
 $\ell \in \Sigma _L$
at which E has bad reduction, the Kodaira-type of
$\ell \in \Sigma _L$
at which E has bad reduction, the Kodaira-type of
 $E_{/{\mathbb Q}_{\ell }}$
is not
$E_{/{\mathbb Q}_{\ell }}$
is not
 $\operatorname {I}_m$
for any integer
$\operatorname {I}_m$
for any integer
 $m\in {\mathbb Z}_{\geq 1}$
;
$m\in {\mathbb Z}_{\geq 1}$
; -
(v)
 is finite.
is finite.
Then,
![]() and at least one of the following is true:
and at least one of the following is true:
-
(a)
 $\operatorname {\mathrm {rank}}_{{\mathbb Z}} E(L)>0$
;
$\operatorname {\mathrm {rank}}_{{\mathbb Z}} E(L)>0$
; -
(b)
 .
.
In particular, the Selmer group
![]() $\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/L)$
becomes nonzero.
$\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/L)$
becomes nonzero.
Remark 4.2. Condition (iv) is automatically satisfied when E has good reduction at all primes
![]() $\ell \in \Sigma _L$
. In a preprint from 2014, J. Brau has made an attempt at a comparable result on the growth of Selmer groups (see [Reference BrauBra14, Corollary 1.3]). Our methods differ significantly from those of Brau and do not require the semi-stability hypothesis.
$\ell \in \Sigma _L$
. In a preprint from 2014, J. Brau has made an attempt at a comparable result on the growth of Selmer groups (see [Reference BrauBra14, Corollary 1.3]). Our methods differ significantly from those of Brau and do not require the semi-stability hypothesis.
To prove the above result, we briefly recall some key properties of the Euler characteristic associated to an elliptic curve. The reader is referred to [Reference Coates and SujathaCS00, Reference Ray and SujathaRS19, Reference Ray and SujathaRS20] for a more comprehensive discussion of the topic.
Let
![]() $E_{/{\mathbb Q}}$
be an elliptic curve and
$E_{/{\mathbb Q}}$
be an elliptic curve and
![]() $L/{\mathbb Q}$
a number field extension. Assume that the following conditions are satisfied:
$L/{\mathbb Q}$
a number field extension. Assume that the following conditions are satisfied:
-
(i)
 $\operatorname {\mathrm {rank}}_{{\mathbb Z}} E(L)=0$
;
$\operatorname {\mathrm {rank}}_{{\mathbb Z}} E(L)=0$
; -
(ii) E has good ordinary reduction at p;
-
(iii)
 is finite.
is finite.
Then, the cohomology groups
![]() $H^i(L_{\operatorname {\mathrm {cyc}}}/L, \operatorname {\mathrm {Sel}}_{p^{\infty }}(E/L_{\operatorname {\mathrm {cyc}}}))$
are finite and the Euler characteristic
$H^i(L_{\operatorname {\mathrm {cyc}}}/L, \operatorname {\mathrm {Sel}}_{p^{\infty }}(E/L_{\operatorname {\mathrm {cyc}}}))$
are finite and the Euler characteristic
![]() $\chi (L_{\operatorname {\mathrm {cyc}}}/L, E[p^{\infty }])$
is defined as follows:
$\chi (L_{\operatorname {\mathrm {cyc}}}/L, E[p^{\infty }])$
is defined as follows:
 $$ \begin{align*} \chi(L_{\operatorname{\mathrm{cyc}}}/L, E[p^{\infty}]):=\frac{\# H^0(L_{\operatorname{\mathrm{cyc}}}/L, \operatorname{\mathrm{Sel}}_{p^{\infty}}(E/L_{\operatorname{\mathrm{cyc}}}))}{\# H^1(L_{\operatorname{\mathrm{cyc}}}/L, \operatorname{\mathrm{Sel}}_{p^{\infty}}(E/L_{\operatorname{\mathrm{cyc}}}))}. \end{align*} $$
$$ \begin{align*} \chi(L_{\operatorname{\mathrm{cyc}}}/L, E[p^{\infty}]):=\frac{\# H^0(L_{\operatorname{\mathrm{cyc}}}/L, \operatorname{\mathrm{Sel}}_{p^{\infty}}(E/L_{\operatorname{\mathrm{cyc}}}))}{\# H^1(L_{\operatorname{\mathrm{cyc}}}/L, \operatorname{\mathrm{Sel}}_{p^{\infty}}(E/L_{\operatorname{\mathrm{cyc}}}))}. \end{align*} $$
The Euler characteristic is an important invariant associated to the Selmer group, and captures its key Iwasawa theoretic properties. There is an explicit formula for this invariant, which we now describe. At each prime
![]() $v\nmid p$
of L, let
$v\nmid p$
of L, let
![]() $c_v(E/L)$
denote the Tamagawa number at v, and let
$c_v(E/L)$
denote the Tamagawa number at v, and let
![]() $c_v^{(p)}(E/L)$
be the p-part, given by
$c_v^{(p)}(E/L)$
be the p-part, given by
![]() $c_v^{(p)}(E/L):=|c_v(E/L)|_p^{-1}$
. Here,
$c_v^{(p)}(E/L):=|c_v(E/L)|_p^{-1}$
. Here,
![]() $|{\cdot }|_p$
is the absolute value, normalized by
$|{\cdot }|_p$
is the absolute value, normalized by
![]() $|{p}|_p=p^{-1}$
. At each prime v of L, let
$|{p}|_p=p^{-1}$
. At each prime v of L, let
![]() $k_v$
be the residue field at v and
$k_v$
be the residue field at v and
![]() $\widetilde {E}(k_v)$
be the group of
$\widetilde {E}(k_v)$
be the group of
![]() $k_v$
-valued points of the reduction of E at v.
$k_v$
-valued points of the reduction of E at v.
Theorem 4.3. Let
![]() $E_{/{\mathbb Q}}$
be an elliptic curve, p an odd prime, and
$E_{/{\mathbb Q}}$
be an elliptic curve, p an odd prime, and
![]() $L/{\mathbb Q}$
be a number field extension. Assume that the following conditions are satisfied:
$L/{\mathbb Q}$
be a number field extension. Assume that the following conditions are satisfied:
-
(i)
 $\operatorname {\mathrm {rank}}_{{\mathbb Z}} E(L)=0$
;
$\operatorname {\mathrm {rank}}_{{\mathbb Z}} E(L)=0$
; -
(ii) E has good ordinary reduction at p;
-
(iii)
 is finite.
is finite.
Then, the following assertions hold:
-
(a) the Euler characteristic
 $\chi (L_{\operatorname {\mathrm {cyc}}}/L, E[p^{\infty }])$
is an integer, further, it is a power of p;
$\chi (L_{\operatorname {\mathrm {cyc}}}/L, E[p^{\infty }])$
is an integer, further, it is a power of p; -
(b) the Euler characteristic is given by the following formula:
(4-1)
Proof. Assertion (a) follows from [Reference Hatley, Kundu and RayHKR21, Lemma 3.4 and Remark 3.5], and for assertion (b), the reader is referred to [Reference Coates and SujathaCS00, Theorem 3.3].
The next result relates the Euler characteristic and Iwasawa invariants.
Proposition 4.4. Let
![]() $E_{/L}$
be an elliptic curve satisfying the following conditions:
$E_{/L}$
be an elliptic curve satisfying the following conditions:
-
(i) E has good ordinary reduction at all primes
 $v|p$
;
$v|p$
; -
(ii)
 $\operatorname {\mathrm {rank}}_{{\mathbb Z}} E(L)=0$
;
$\operatorname {\mathrm {rank}}_{{\mathbb Z}} E(L)=0$
; -
(iii)
 is finite.
is finite.
Then, the following are equivalent:
-
(a)
 $\mu _p(E/L)=0$
and
$\mu _p(E/L)=0$
and
 $\lambda _p(E/L)=0$
;
$\lambda _p(E/L)=0$
; -
(b)
 $\chi (L_{\operatorname {\mathrm {cyc}}}/L, E[p^{\infty }])=1$
.
$\chi (L_{\operatorname {\mathrm {cyc}}}/L, E[p^{\infty }])=1$
.
Proof. The conditions on the elliptic curve are in place for the Euler characteristic to be defined. The result follows from [Reference Hatley, Kundu and RayHKR21, Proposition 3.6]. However, the first proof of this result was given in [Reference Ray and SujathaRS19], in a more general context.
Lemma 4.5. Let
![]() $E_{/{\mathbb Q}}$
be an elliptic curve that satisfies the following conditions:
$E_{/{\mathbb Q}}$
be an elliptic curve that satisfies the following conditions:
-
(i) E has good ordinary reduction at p;
-
(ii)
 is finite;
is finite; -
(iii)
 $\operatorname {\mathrm {rank}}_{{\mathbb Z}}E({\mathbb Q})=0$
;
$\operatorname {\mathrm {rank}}_{{\mathbb Z}}E({\mathbb Q})=0$
; -
(iv)
 $E({\mathbb Q})[p^{\infty }]=0$
;
$E({\mathbb Q})[p^{\infty }]=0$
; -
(v)
 $\mu _p(E/{\mathbb Q})=0$
and
$\mu _p(E/{\mathbb Q})=0$
and
 $\lambda _p(E/{\mathbb Q})=0$
.
$\lambda _p(E/{\mathbb Q})=0$
.
Then, we have that
![]() .
.
Proof. Recall the well-known short exact sequence (see Equation (2-2)),
Since
![]() $E({\mathbb Q})$
is finite and
$E({\mathbb Q})$
is finite and
![]() $E({\mathbb Q})[p^{\infty }]=0$
, it follows from the above that
$E({\mathbb Q})[p^{\infty }]=0$
, it follows from the above that
It follows from Proposition 4.4 that
![]() $\chi ({\mathbb Q}_{\operatorname {\mathrm {cyc}}}/{\mathbb Q}, E[p^{\infty }])=1$
. However, by Equation (4-1),
$\chi ({\mathbb Q}_{\operatorname {\mathrm {cyc}}}/{\mathbb Q}, E[p^{\infty }])=1$
. However, by Equation (4-1),
As a result, it is indeed the case that
.
Lemma 4.6. Let
![]() $p\geq 5$
be a prime,
$p\geq 5$
be a prime,
![]() $L/{\mathbb Q}$
be a
$L/{\mathbb Q}$
be a
![]() ${\mathbb Z}/p{\mathbb Z}$
extension, and
${\mathbb Z}/p{\mathbb Z}$
extension, and
![]() $\ell \neq p$
be a prime that ramifies in L. Assume that the Kodaira type of
$\ell \neq p$
be a prime that ramifies in L. Assume that the Kodaira type of
![]() $E_{/{\mathbb Q}_{\ell }}$
is not
$E_{/{\mathbb Q}_{\ell }}$
is not
![]() $\operatorname {I}_m$
for any integer
$\operatorname {I}_m$
for any integer
![]() ${m\in {\mathbb Z}_{\geq 1}}$
. Then,
${m\in {\mathbb Z}_{\geq 1}}$
. Then,
![]() $\prod _{v\mid \ell } c_v^{(p)}(E/L)=1$
.
$\prod _{v\mid \ell } c_v^{(p)}(E/L)=1$
.
Proof. Since
![]() $\ell \neq p$
and
$\ell \neq p$
and
![]() $L/{\mathbb Q}$
is a
$L/{\mathbb Q}$
is a
![]() ${\mathbb Z}/p{\mathbb Z}$
-extension, it follows that
${\mathbb Z}/p{\mathbb Z}$
-extension, it follows that
![]() $\ell $
is tamely ramified in L. Thus, the results for base-change of Tamagawa numbers in [Reference KidaKid03, Table 1, pages 556–557] apply. Fix a prime
$\ell $
is tamely ramified in L. Thus, the results for base-change of Tamagawa numbers in [Reference KidaKid03, Table 1, pages 556–557] apply. Fix a prime
![]() $v|\ell $
and let
$v|\ell $
and let
![]() $e=e_{L/{\mathbb Q}}(v)$
be the ramification index. Since it is assumed that
$e=e_{L/{\mathbb Q}}(v)$
be the ramification index. Since it is assumed that
![]() $\ell $
is ramified in L, it follows that
$\ell $
is ramified in L, it follows that
![]() $e=p$
. Since
$e=p$
. Since
![]() $p\geq 5$
, the Tamagawa number
$p\geq 5$
, the Tamagawa number
![]() $c_v^{(p)}(E/L)\neq 1$
if and only if the Kodaira type of
$c_v^{(p)}(E/L)\neq 1$
if and only if the Kodaira type of
![]() $E_{/L_v}$
is
$E_{/L_v}$
is
![]() $\operatorname {I}_n$
for an integer
$\operatorname {I}_n$
for an integer
![]() $n\in {\mathbb Z}_{\geq 1}$
that is divisible by p (see [Reference SilvermanSil09, page 448]). According to [Reference SilvermanSil09, page 448], the only way this is possible is if the Kodaira type of
$n\in {\mathbb Z}_{\geq 1}$
that is divisible by p (see [Reference SilvermanSil09, page 448]). According to [Reference SilvermanSil09, page 448], the only way this is possible is if the Kodaira type of
![]() $E_{/{\mathbb Q}_{\ell }}$
is
$E_{/{\mathbb Q}_{\ell }}$
is
![]() $\operatorname {I}_m$
for
$\operatorname {I}_m$
for
![]() $m\in {\mathbb Z}_{\geq 1}$
. Indeed, if the Kodaira type of
$m\in {\mathbb Z}_{\geq 1}$
. Indeed, if the Kodaira type of
![]() $E_{/{\mathbb Q}_{\ell }}$
is
$E_{/{\mathbb Q}_{\ell }}$
is
![]() $\operatorname {I}_m$
, then upon base-change to
$\operatorname {I}_m$
, then upon base-change to
![]() $L_v$
, it becomes
$L_v$
, it becomes
![]() $\operatorname {I}_{me}=\operatorname {I}_{mp}$
. However, by assumption, this case does not occur. Therefore,
$\operatorname {I}_{me}=\operatorname {I}_{mp}$
. However, by assumption, this case does not occur. Therefore,
![]() $c_v^{(p)}(E/L)=1$
for all primes
$c_v^{(p)}(E/L)=1$
for all primes
![]() $v|\ell $
of L. This completes the proof.
$v|\ell $
of L. This completes the proof.
We now give a proof of Proposition 4.1.
Proof of Proposition 4.1. According to Lemma 4.5, we have that
Assume by way of contradiction that
Since
![]() $\operatorname {\mathrm {rank}}_{{\mathbb Z}} E(L)=0$
, it follows from Theorem 4.3 that the Euler characteristic
$\operatorname {\mathrm {rank}}_{{\mathbb Z}} E(L)=0$
, it follows from Theorem 4.3 that the Euler characteristic
![]() $\chi (L_{\operatorname {\mathrm {cyc}}}/L, E[p^{\infty }])$
is defined and given by the formula
$\chi (L_{\operatorname {\mathrm {cyc}}}/L, E[p^{\infty }])$
is defined and given by the formula

However, the Euler characteristic
![]() $\chi ({\mathbb Q}_{\operatorname {\mathrm {cyc}}}/{\mathbb Q}, E[p^{\infty }])$
is given by the formula
$\chi ({\mathbb Q}_{\operatorname {\mathrm {cyc}}}/{\mathbb Q}, E[p^{\infty }])$
is given by the formula
Note that
![]() $E({\mathbb Q})[p^{\infty }]$
does not contribute to the above formula since it is assumed to be trivial. Since it is assumed that
$E({\mathbb Q})[p^{\infty }]$
does not contribute to the above formula since it is assumed to be trivial. Since it is assumed that
![]() $\mu _p(E/{\mathbb Q})=0$
and
$\mu _p(E/{\mathbb Q})=0$
and
![]() $\lambda _p(E/{\mathbb Q})=0$
, it follows from Proposition 4.4 that
$\lambda _p(E/{\mathbb Q})=0$
, it follows from Proposition 4.4 that
![]() $\chi ({\mathbb Q}_{\operatorname {\mathrm {cyc}}}/{\mathbb Q}, E[p^{\infty }])=1$
.
$\chi ({\mathbb Q}_{\operatorname {\mathrm {cyc}}}/{\mathbb Q}, E[p^{\infty }])=1$
.
We use this and the assumptions on E to show that
![]() $\chi (L_{\operatorname {\mathrm {cyc}}}/L, E[p^{\infty }])=1$
as well. Since
$\chi (L_{\operatorname {\mathrm {cyc}}}/L, E[p^{\infty }])=1$
as well. Since
![]() $\chi ({\mathbb Q}_{\operatorname {\mathrm {cyc}}}/{\mathbb Q}, E[p^{\infty }])=1$
, it follows that
$\chi ({\mathbb Q}_{\operatorname {\mathrm {cyc}}}/{\mathbb Q}, E[p^{\infty }])=1$
, it follows that
To show that
![]() $\chi (L_{\operatorname {\mathrm {cyc}}}/L, E[p^{\infty }])=1$
, we show that
$\chi (L_{\operatorname {\mathrm {cyc}}}/L, E[p^{\infty }])=1$
, we show that

By assumption,
, and hence,
. It follows from Lemma 4.6 that
![]() $\prod _{v\nmid p}c_v^{(p)}(E/L)=1$
. If p splits or ramifies in L, then
$\prod _{v\nmid p}c_v^{(p)}(E/L)=1$
. If p splits or ramifies in L, then
![]() $k_v={\mathbb F}_p$
for all primes
$k_v={\mathbb F}_p$
for all primes
![]() $v|p$
. Since
$v|p$
. Since
![]() $\#\widetilde {E}({\mathbb F}_p)[p^{\infty }]=1$
, it follows that
$\#\widetilde {E}({\mathbb F}_p)[p^{\infty }]=1$
, it follows that
![]() $\#\widetilde {E}(k_v)[p^{\infty }]=1$
as well. However, suppose p is inert in L and
$\#\widetilde {E}(k_v)[p^{\infty }]=1$
as well. However, suppose p is inert in L and
![]() $v|p$
is the only prime above p in L. Then, since
$v|p$
is the only prime above p in L. Then, since
![]() $k_v/{\mathbb F}_p$
is a p-extension, it follows from [Reference Neukirch, Schmidt and WingbergNSW13, Proposition 1.6.12] that
$k_v/{\mathbb F}_p$
is a p-extension, it follows from [Reference Neukirch, Schmidt and WingbergNSW13, Proposition 1.6.12] that
Hence, the numerator of Equation (4-2) is
![]() $1$
. Theorem 4.3 asserts the Euler characteristic is an integer, and so, we deduce that
$1$
. Theorem 4.3 asserts the Euler characteristic is an integer, and so, we deduce that
![]() $\chi (L_{\operatorname {\mathrm {cyc}}}/L, E[p^{\infty }])=1$
. We deduce from Proposition 4.4 that
$\chi (L_{\operatorname {\mathrm {cyc}}}/L, E[p^{\infty }])=1$
. We deduce from Proposition 4.4 that
In particular, we find that
However, recall that according to Kida’s formula,
 $$ \begin{align*} \lambda_p(E/L)=p\lambda_p(E/{\mathbb Q})+\sum_{w \in P_1} (e_{L/{\mathbb Q}}(w/\ell)-1)+\sum_{w \in P_2} 2(e_{L/{\mathbb Q}}(w/\ell)-1).\end{align*} $$
$$ \begin{align*} \lambda_p(E/L)=p\lambda_p(E/{\mathbb Q})+\sum_{w \in P_1} (e_{L/{\mathbb Q}}(w/\ell)-1)+\sum_{w \in P_2} 2(e_{L/{\mathbb Q}}(w/\ell)-1).\end{align*} $$
However, there is a prime
![]() $\ell \in \Sigma _L$
for which E has good reduction at
$\ell \in \Sigma _L$
for which E has good reduction at
![]() $\ell $
and
$\ell $
and
![]() $p| \#\widetilde {E}({\mathbb F}_{\ell })$
, so we deduce that
$p| \#\widetilde {E}({\mathbb F}_{\ell })$
, so we deduce that
 $$ \begin{align*} \sum_{w \in P_2} 2(e_{L/{\mathbb Q}}(w/\ell)-1)>0. \end{align*} $$
$$ \begin{align*} \sum_{w \in P_2} 2(e_{L/{\mathbb Q}}(w/\ell)-1)>0. \end{align*} $$
Thus, the above formula shows that
In particular,
![]() $\lambda _p(E/L)>0$
, this is a contradiction. Therefore, we have shown that either
$\lambda _p(E/L)>0$
, this is a contradiction. Therefore, we have shown that either
![]() $\operatorname {\mathrm {rank}}_{{\mathbb Z}} E(L)>0$
or
$\operatorname {\mathrm {rank}}_{{\mathbb Z}} E(L)>0$
or
.
We illustrate Proposition 4.1 through an example in the case when
![]() $p=5$
.
$p=5$
.
Example. Let
![]() $L/{\mathbb Q}$
be the unique degree
$L/{\mathbb Q}$
be the unique degree
![]() $5$
Galois extension contained in
$5$
Galois extension contained in
![]() ${\mathbb Q}(\mu _{31})$
. The only prime that ramifies in L is
${\mathbb Q}(\mu _{31})$
. The only prime that ramifies in L is
![]() $\ell =31$
. Consider the elliptic curve
$\ell =31$
. Consider the elliptic curve
![]() $E: y^2=x^3+42$
. Explicit calculation shows that E satisfies conditions (i)–(iv) of the aforementioned proposition. Assuming the finiteness of the Shafarevich–Tate group over L, we conclude that either there is a rank jump or an increase in the size of the Shafarevich–Tate group. It can be checked via standard computations on Magma that
$E: y^2=x^3+42$
. Explicit calculation shows that E satisfies conditions (i)–(iv) of the aforementioned proposition. Assuming the finiteness of the Shafarevich–Tate group over L, we conclude that either there is a rank jump or an increase in the size of the Shafarevich–Tate group. It can be checked via standard computations on Magma that
![]() $E(L)=E({\mathbb Q})$
. Therefore, the growth occurs in the Shafarevich–Tate group.
$E(L)=E({\mathbb Q})$
. Therefore, the growth occurs in the Shafarevich–Tate group.
4.2
We now come to an application to arithmetic statistics. Recall that we fix an elliptic curve
![]() $E_{/{\mathbb Q}}$
and a prime p for which the aforementioned conditions are satisfied. Consider the family of
$E_{/{\mathbb Q}}$
and a prime p for which the aforementioned conditions are satisfied. Consider the family of
![]() ${\mathbb Z}/p{\mathbb Z}$
-extensions L of
${\mathbb Z}/p{\mathbb Z}$
-extensions L of
![]() ${\mathbb Q}$
not contained in
${\mathbb Q}$
not contained in
![]() ${\mathbb Q}_{\operatorname {\mathrm {cyc}}}$
and ramified at precisely one prime. For each prime
${\mathbb Q}_{\operatorname {\mathrm {cyc}}}$
and ramified at precisely one prime. For each prime
![]() $q\equiv 1\ \pmod {\,p}$
, there is exactly one such extension
$q\equiv 1\ \pmod {\,p}$
, there is exactly one such extension
![]() $L_q/{\mathbb Q}$
that is ramified at q (see Proposition 3.4). Note that
$L_q/{\mathbb Q}$
that is ramified at q (see Proposition 3.4). Note that
![]() $L_q$
is contained in
$L_q$
is contained in
![]() ${\mathbb Q}(\mu _q)$
. For
${\mathbb Q}(\mu _q)$
. For
![]() $X>0$
, let
$X>0$
, let
![]() $\pi (X)$
be the prime counting function (that is, denote the number of primes
$\pi (X)$
be the prime counting function (that is, denote the number of primes
![]() $q\leq X$
) and
$q\leq X$
) and
![]() $\pi '(X)$
be the number of primes
$\pi '(X)$
be the number of primes
![]() $q\leq X$
for which:
$q\leq X$
for which:
-
(i)
 $q\equiv 1\ \pmod {\,p}$
; and
$q\equiv 1\ \pmod {\,p}$
; and -
(ii)
 $\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/L_q)\neq 0$
.
$\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/L_q)\neq 0$
.
Note that since
![]() $L_q/{\mathbb Q}$
is a
$L_q/{\mathbb Q}$
is a
![]() ${\mathbb Z}/p{\mathbb Z}$
-extension, we have the following implication:
${\mathbb Z}/p{\mathbb Z}$
-extension, we have the following implication:
see [Reference Neukirch, Schmidt and WingbergNSW13, Proposition 1.6.12]. Therefore, the nonvanishing of
![]() $\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/L_q)$
is equivalent to at least one of the following conditions being satisfied:
$\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/L_q)$
is equivalent to at least one of the following conditions being satisfied:
-
(1)
 $\operatorname {\mathrm {rank}}_{{\mathbb Z}}E(L_q)>0$
;
$\operatorname {\mathrm {rank}}_{{\mathbb Z}}E(L_q)>0$
; -
(2)
 .
.
Thus, if the Selmer group becomes nonzero after base-change, then either there is a rank jump or the Shafarevich–Tate group witnesses growth. The main result of this section is Theorem 4.9, where it is shown that the set of primes
![]() $q\equiv 1\ \pmod {\,p}$
for which the above conditions are satisfied is cut out by explicit Chebotarev conditions. In other words, there is an explicit subset
$q\equiv 1\ \pmod {\,p}$
for which the above conditions are satisfied is cut out by explicit Chebotarev conditions. In other words, there is an explicit subset
![]() $\mathcal {S}\subset \operatorname {\mathrm {Gal}}({\mathbb Q}(E[p])/{\mathbb Q})$
such that for any prime
$\mathcal {S}\subset \operatorname {\mathrm {Gal}}({\mathbb Q}(E[p])/{\mathbb Q})$
such that for any prime
![]() $q\neq p$
coprime to the conductor of E,
$q\neq p$
coprime to the conductor of E,
Therefore, if the Frobenius of a prime
![]() $q\nmid Np$
lies in the Chebotarev set
$q\nmid Np$
lies in the Chebotarev set
![]() $\mathcal {S}$
, then the Selmer group becomes nonzero when base changed to
$\mathcal {S}$
, then the Selmer group becomes nonzero when base changed to
![]() $L_q$
. We calculate the size of
$L_q$
. We calculate the size of
![]() $\mathcal {S}$
and apply the Chebotarev density theorem to obtain a lower bound for
$\mathcal {S}$
and apply the Chebotarev density theorem to obtain a lower bound for
![]() $\limsup _{X\rightarrow \infty } \pi '(X)/\pi (X)$
. Stated differently, we are able to show there is growth in the Selmer group in
$\limsup _{X\rightarrow \infty } \pi '(X)/\pi (X)$
. Stated differently, we are able to show there is growth in the Selmer group in
![]() $L_q$
for a positive density set of primes q. Let
$L_q$
for a positive density set of primes q. Let
![]() $\bar {\rho }:\operatorname {\mathrm {Gal}}(\bar {{\mathbb Q}}/{\mathbb Q})\rightarrow \operatorname {\mathrm {GL}}_2({\mathbb F}_p)$
be the Galois representation on
$\bar {\rho }:\operatorname {\mathrm {Gal}}(\bar {{\mathbb Q}}/{\mathbb Q})\rightarrow \operatorname {\mathrm {GL}}_2({\mathbb F}_p)$
be the Galois representation on
![]() $E[p]$
. We make the simplifying assumption that
$E[p]$
. We make the simplifying assumption that
![]() $\bar {\rho }$
is surjective. By the well-known open image theorem of Serre, this assumption is satisfied for all but finitely many primes p, as long as E does not have complex multiplication. Let
$\bar {\rho }$
is surjective. By the well-known open image theorem of Serre, this assumption is satisfied for all but finitely many primes p, as long as E does not have complex multiplication. Let
![]() ${\mathbb Q}(E[p])$
be the Galois extension of
${\mathbb Q}(E[p])$
be the Galois extension of
![]() ${\mathbb Q}$
that is fixed by
${\mathbb Q}$
that is fixed by
![]() $\ker \bar {\rho }$
. We identify
$\ker \bar {\rho }$
. We identify
![]() $\operatorname {\mathrm {Gal}}({\mathbb Q}(E[p])/{\mathbb Q})$
with its image under
$\operatorname {\mathrm {Gal}}({\mathbb Q}(E[p])/{\mathbb Q})$
with its image under
![]() $\bar {\rho }$
, which, according to our assumption, is all of
$\bar {\rho }$
, which, according to our assumption, is all of
![]() $\operatorname {\mathrm {GL}}_2({\mathbb F}_p)$
. Let
$\operatorname {\mathrm {GL}}_2({\mathbb F}_p)$
. Let
![]() $N=N_E$
be the conductor of E. If q is a prime that is coprime to
$N=N_E$
be the conductor of E. If q is a prime that is coprime to
![]() $N p$
, then q is unramified in
$N p$
, then q is unramified in
![]() ${\mathbb Q}(E[p])$
. Set
${\mathbb Q}(E[p])$
. Set
![]() $a_q(E):=q+1-\# \widetilde {E}({\mathbb F}_q)$
; then the characteristic polynomial of
$a_q(E):=q+1-\# \widetilde {E}({\mathbb F}_q)$
; then the characteristic polynomial of
![]() $\bar {\rho }(\operatorname {\mathrm {Frob}}_q)$
is
$\bar {\rho }(\operatorname {\mathrm {Frob}}_q)$
is
![]() $x^2-a_q x+q$
. Let
$x^2-a_q x+q$
. Let
![]() $\mathcal {S}$
consist of elements
$\mathcal {S}$
consist of elements
![]() $\sigma \in \operatorname {\mathrm {Gal}}({\mathbb Q}(E[p])/{\mathbb Q})$
such that
$\sigma \in \operatorname {\mathrm {Gal}}({\mathbb Q}(E[p])/{\mathbb Q})$
such that
We arrive at the following useful criterion for p to divide
![]() $\#\widetilde {E}({\mathbb F}_q)$
.
$\#\widetilde {E}({\mathbb F}_q)$
.
Lemma 4.7. Let
![]() $q\nmid N p$
be a prime. Then, the following conditions are equivalent:
$q\nmid N p$
be a prime. Then, the following conditions are equivalent:
-
(i)
 $q\equiv 1\ \pmod {\,p}$
and p divides
$q\equiv 1\ \pmod {\,p}$
and p divides
 $\#\widetilde {E}({\mathbb F}_q)$
;
$\#\widetilde {E}({\mathbb F}_q)$
; -
(ii)
 $\operatorname {\mathrm {Frob}}_q\in \mathcal {S}$
.
$\operatorname {\mathrm {Frob}}_q\in \mathcal {S}$
.
Proof. Since
![]() $\det \bar {\rho }(\operatorname {\mathrm {Frob}}_q)=q$
, we find that
$\det \bar {\rho }(\operatorname {\mathrm {Frob}}_q)=q$
, we find that
![]() $\det \bar {\rho }(\operatorname {\mathrm {Frob}}_q)=1$
if and only if
$\det \bar {\rho }(\operatorname {\mathrm {Frob}}_q)=1$
if and only if
![]() $q\equiv 1\ \pmod {\,p}$
. Assume that these equivalent conditions are satisfied. Note that p divides
$q\equiv 1\ \pmod {\,p}$
. Assume that these equivalent conditions are satisfied. Note that p divides
![]() $\# \widetilde {E}({\mathbb F}_q)$
if and only if
$\# \widetilde {E}({\mathbb F}_q)$
if and only if
![]() $q+1-\operatorname {\mathrm {trace}}(\bar {\rho }(\operatorname {\mathrm {Frob}}_q))=0$
. Since
$q+1-\operatorname {\mathrm {trace}}(\bar {\rho }(\operatorname {\mathrm {Frob}}_q))=0$
. Since
![]() $q\equiv 1\ \pmod {\,p}$
, it follows that p divides
$q\equiv 1\ \pmod {\,p}$
, it follows that p divides
![]() $\# \widetilde {E}({\mathbb F}_q)$
if and only if
$\# \widetilde {E}({\mathbb F}_q)$
if and only if
![]() $\operatorname {\mathrm {trace}}(\bar {\rho }(\operatorname {\mathrm {Frob}}_q))=2$
.
$\operatorname {\mathrm {trace}}(\bar {\rho }(\operatorname {\mathrm {Frob}}_q))=2$
.
Lemma 4.8. The cardinality of
![]() $\mathcal {S}$
is
$\mathcal {S}$
is
![]() $p^2$
.
$p^2$
.
Proof. Since
![]() $\bar {\rho }$
is assumed to be surjective, we identify
$\bar {\rho }$
is assumed to be surjective, we identify
![]() $\mathcal {S}$
with the set of all matrices in
$\mathcal {S}$
with the set of all matrices in
![]() $\operatorname {\mathrm {GL}}_2({\mathbb F}_p)$
with trace
$\operatorname {\mathrm {GL}}_2({\mathbb F}_p)$
with trace
![]() $2$
and determinant
$2$
and determinant
![]() $1$
. These matrices are all of the form
$1$
. These matrices are all of the form
![]() $g=(\begin {smallmatrix} a & b \\ c & 2-a \end {smallmatrix})$
, where
$g=(\begin {smallmatrix} a & b \\ c & 2-a \end {smallmatrix})$
, where
![]() $a(2-a)-bc=1$
. We count the number of such matrices. Rewrite the equation as
$a(2-a)-bc=1$
. We count the number of such matrices. Rewrite the equation as
![]() $bc=-1+a(2-a)=-(a-1)^2$
. For each choice of a such that
$bc=-1+a(2-a)=-(a-1)^2$
. For each choice of a such that
![]() $a\neq 1$
, the number of solutions is
$a\neq 1$
, the number of solutions is
![]() $(p-1)$
. For
$(p-1)$
. For
![]() $a=1$
, either
$a=1$
, either
![]() $b=0$
or
$b=0$
or
![]() $c=0$
, or both. Thus, the number of solutions for
$c=0$
, or both. Thus, the number of solutions for
![]() $a=1$
is
$a=1$
is
![]() $2p-1$
. Putting it all together,
$2p-1$
. Putting it all together,
We now prove Theorem B, which is the main result of this section.
Theorem 4.9. Let
![]() $p\geq 5$
be a fixed prime and
$p\geq 5$
be a fixed prime and
![]() $E_{/{\mathbb Q}}$
an elliptic curve for which the following conditions are satisfied:
$E_{/{\mathbb Q}}$
an elliptic curve for which the following conditions are satisfied:
-
(i) E has good ordinary reduction at p;
-
(ii)
 $\operatorname {\mathrm {rank}}_{{\mathbb Z}} E({\mathbb Q})=0$
and
$\operatorname {\mathrm {rank}}_{{\mathbb Z}} E({\mathbb Q})=0$
and
 $E({\mathbb Q})[p^{\infty }]=0$
;
$E({\mathbb Q})[p^{\infty }]=0$
; -
(iii)
 $\mu _p(E/{\mathbb Q})=0$
and
$\mu _p(E/{\mathbb Q})=0$
and
 $\lambda _p(E/{\mathbb Q})=0$
;
$\lambda _p(E/{\mathbb Q})=0$
; -
(iv) the image of the residual representation
 $\bar {\rho }$
is surjective.
$\bar {\rho }$
is surjective.
For
![]() $X>0$
, let
$X>0$
, let
![]() $\pi '(X)$
be the number of primes
$\pi '(X)$
be the number of primes
![]() $q\equiv 1\ \pmod {\,p}$
for which the following equivalent conditions are satisfied:
$q\equiv 1\ \pmod {\,p}$
for which the following equivalent conditions are satisfied:
-
(i)
 $\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/L_q)\neq 0$
;
$\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/L_q)\neq 0$
; -
(ii) either,
 $\operatorname {\mathrm {rank}}_{{\mathbb Z}} E(L_q)>0$
or
$\operatorname {\mathrm {rank}}_{{\mathbb Z}} E(L_q)>0$
or
 (or both conditions are satisfied).
(or both conditions are satisfied).
Then,
 $$ \begin{align*} \limsup_{X\rightarrow \infty} \frac{\pi'(X)}{\pi(X)}\geq \frac{p}{(p-1)^2(p+1)}. \end{align*} $$
$$ \begin{align*} \limsup_{X\rightarrow \infty} \frac{\pi'(X)}{\pi(X)}\geq \frac{p}{(p-1)^2(p+1)}. \end{align*} $$
Proof. Let q be a prime such that
![]() $q\nmid N p$
. It follows from Lemma 4.7 that if
$q\nmid N p$
. It follows from Lemma 4.7 that if
![]() $\operatorname {\mathrm {Frob}}_q\in \mathcal {S}$
, then
$\operatorname {\mathrm {Frob}}_q\in \mathcal {S}$
, then
![]() $q\equiv 1\ \pmod {\,p}$
and
$q\equiv 1\ \pmod {\,p}$
and
![]() $p|\#E({\mathbb F}_q)$
. Note that
$p|\#E({\mathbb F}_q)$
. Note that
![]() $\Sigma _{L_q}=\{q\}$
and E has good reduction at q. Since
$\Sigma _{L_q}=\{q\}$
and E has good reduction at q. Since
![]() $p|\#E({\mathbb F}_q)$
, it follows from Proposition 4.1 that
$p|\#E({\mathbb F}_q)$
, it follows from Proposition 4.1 that
![]() $\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/L_q)\neq 0$
. Therefore, by the Chebotarev density theorem and Lemma 4.8,
$\operatorname {\mathrm {Sel}}_{p^{\infty }}(E/L_q)\neq 0$
. Therefore, by the Chebotarev density theorem and Lemma 4.8,
 $$ \begin{align*} \limsup_{X\rightarrow\infty} \frac{\pi'(X)}{\pi(X)}\geq \frac{\# \mathcal{S}}{\#(\operatorname{\mathrm{GL}}_2({\mathbb F}_p))}=\frac{p^2}{(p^2-1)(p^2-p)}=\frac{p}{(p-1)^2(p+1)}.\\[-42pt] \end{align*} $$
$$ \begin{align*} \limsup_{X\rightarrow\infty} \frac{\pi'(X)}{\pi(X)}\geq \frac{\# \mathcal{S}}{\#(\operatorname{\mathrm{GL}}_2({\mathbb F}_p))}=\frac{p^2}{(p^2-1)(p^2-p)}=\frac{p}{(p-1)^2(p+1)}.\\[-42pt] \end{align*} $$
5 Growth of Shafarevich–Tate groups in cyclic extensions
In this section, we study the growth of the Shafarevich–Tate group. First, when
![]() $p=2$
, we prove an effective version of Matsuno’s theorem (see Theorem 5.4).
$p=2$
, we prove an effective version of Matsuno’s theorem (see Theorem 5.4).
When
![]() $p\neq 2$
, it was shown by Clark and Sharif (see [Reference Clark and SharifCS10, Theorem 3]) that there exists a degree-p extension over
$p\neq 2$
, it was shown by Clark and Sharif (see [Reference Clark and SharifCS10, Theorem 3]) that there exists a degree-p extension over
![]() ${\mathbb Q}$
, not necessarily Galois, such that the p-rank of the Shafarevich–Tate group becomes arbitrarily large. We study the possibility of improving this result to Galois degree-p extensions.
${\mathbb Q}$
, not necessarily Galois, such that the p-rank of the Shafarevich–Tate group becomes arbitrarily large. We study the possibility of improving this result to Galois degree-p extensions.
Definition 5.1. Let p be any prime. Fix an elliptic curve
![]() $E_{/{\mathbb Q}}$
with good reduction at p. Let
$E_{/{\mathbb Q}}$
with good reduction at p. Let
![]() $K/{\mathbb Q}$
be a cyclic degree-p extension. Define the set
$K/{\mathbb Q}$
be a cyclic degree-p extension. Define the set
![]() $T_{E/K}$
to be the set of primes in K above
$T_{E/K}$
to be the set of primes in K above
![]() $\ell\ (\neq p)$
satisfying either of the following properties:
$\ell\ (\neq p)$
satisfying either of the following properties:
-
(i)
 $\ell $
is a prime of good reduction of E that is ramified in
$\ell $
is a prime of good reduction of E that is ramified in
 $K/{\mathbb Q}$
and
$K/{\mathbb Q}$
and
 $E({\mathbb Q}_{\ell })$
contains an element of order p;
$E({\mathbb Q}_{\ell })$
contains an element of order p; -
(ii)
 $\ell $
is a prime of split multiplicative reduction that is inert in
$\ell $
is a prime of split multiplicative reduction that is inert in
 $K/{\mathbb Q}$
and the Tamagawa number
$K/{\mathbb Q}$
and the Tamagawa number
 $c_{\ell }$
is divisible by p.
$c_{\ell }$
is divisible by p.
Definition 5.2. Let G be an abelian group. Define the p-rank of G as
The following lemma plays a key role in answering questions pertaining to both sections.
Lemma 5.3. With notation as above,
Proof. See [Reference MatsunoMat09, Proposition 4.3].
5.1 Large 2-rank of the Shafarevich–Tate group in quadratic extensions
Given an elliptic curve
![]() $E_{/{\mathbb Q}}$
, it is known that the 2-part of the Shafarevich–Tate group becomes arbitrarily large over some quadratic extension. More precisely, we get the following theorem.
$E_{/{\mathbb Q}}$
, it is known that the 2-part of the Shafarevich–Tate group becomes arbitrarily large over some quadratic extension. More precisely, we get the following theorem.
Theorem 5.4. Given an elliptic curve
![]() $E_{/{\mathbb Q}}$
and a nonnegative integer n, there exists a quadratic number field
$E_{/{\mathbb Q}}$
and a nonnegative integer n, there exists a quadratic number field
![]() $K/{\mathbb Q}$
such that
$K/{\mathbb Q}$
such that
![]() .
.
Proof. See [Reference MatsunoMat09, Proposition B].
A reasonable question to ask is whether the above result can be made effective.
Question 5.5. Given an elliptic curve
![]() $E_{/{\mathbb Q}}$
and a fixed nonnegative integer n, varying over all quadratic number fields ordered by a conductor, what is the minimal conductor of a number field such that one can guarantee
$E_{/{\mathbb Q}}$
and a fixed nonnegative integer n, varying over all quadratic number fields ordered by a conductor, what is the minimal conductor of a number field such that one can guarantee
![]() ?
?
5.1.1 Reviewing the proof of Matsuno’s construction
In this section, we briefly review the proof of Matsuno’s theorem. For details, we refer the reader to the original article [Reference MatsunoMat09]. Fix an elliptic curve
![]() $E_{/{\mathbb Q}}$
of conductor
$E_{/{\mathbb Q}}$
of conductor
![]() $N=N_E$
. Let
$N=N_E$
. Let
![]() $K/{\mathbb Q}$
be a quadratic extension. Let S be a finite set of primes in
$K/{\mathbb Q}$
be a quadratic extension. Let S be a finite set of primes in
![]() ${\mathbb Q}$
containing precisely the prime number 2, the primes of bad reduction of E, and the archimedean primes.
${\mathbb Q}$
containing precisely the prime number 2, the primes of bad reduction of E, and the archimedean primes.
Let
![]() $\ell _1, \ldots , \ell _k$
be odd rational primes that are coprime to N and split completely in
$\ell _1, \ldots , \ell _k$
be odd rational primes that are coprime to N and split completely in
![]() ${\mathbb Q}(E[2])/{\mathbb Q}$
. Recall that
${\mathbb Q}(E[2])/{\mathbb Q}$
. Recall that
![]() ${\mathbb Q}(E[2])/{\mathbb Q}$
is a Galois extension with Galois group isomorphic to either
${\mathbb Q}(E[2])/{\mathbb Q}$
is a Galois extension with Galois group isomorphic to either
![]() ${\mathbb Z}/2{\mathbb Z}$
or
${\mathbb Z}/2{\mathbb Z}$
or
![]() ${\mathbb Z}/3{\mathbb Z}$
or
${\mathbb Z}/3{\mathbb Z}$
or
![]() $S_3$
. By the Chebotarev density theorem, there is a positive proportion of primes that split completely in
$S_3$
. By the Chebotarev density theorem, there is a positive proportion of primes that split completely in
![]() ${\mathbb Q}(E[2])/{\mathbb Q}$
. Having picked the primes
${\mathbb Q}(E[2])/{\mathbb Q}$
. Having picked the primes
![]() $\ell _1, \ldots , \ell _k$
, it is clear that there exists a quadratic extension
$\ell _1, \ldots , \ell _k$
, it is clear that there exists a quadratic extension
![]() $K/{\mathbb Q}$
such that the chosen primes ramify. However, more is true. Results of Waldspurger (see [Reference Bump, Friedberg and HoffsteinBFH90, Theorem in Section 0]) and Kolyvagin (see [Reference KolyvaginKol89]) guarantee the existence of
$K/{\mathbb Q}$
such that the chosen primes ramify. However, more is true. Results of Waldspurger (see [Reference Bump, Friedberg and HoffsteinBFH90, Theorem in Section 0]) and Kolyvagin (see [Reference KolyvaginKol89]) guarantee the existence of
![]() $K/{\mathbb Q}$
such that the chosen primes ramify and the Mordell–Weil rank of
$K/{\mathbb Q}$
such that the chosen primes ramify and the Mordell–Weil rank of
![]() $E^{\prime }({\mathbb Q})$
is 0 where
$E^{\prime }({\mathbb Q})$
is 0 where
![]() $E^{\prime }$
is the quadratic twist of E corresponding to K. It follows that
$E^{\prime }$
is the quadratic twist of E corresponding to K. It follows that
Observe that the primes
![]() $\ell _1, \ldots , \ell _k$
are primes of good ordinary reduction that lie in
$\ell _1, \ldots , \ell _k$
are primes of good ordinary reduction that lie in
![]() $T_{E/K}$
. Therefore, it follows from Lemma 5.3 that
$T_{E/K}$
. Therefore, it follows from Lemma 5.3 that
Using the Kummer sequence, we see that

Even though the results of Waldspurger and Kolyvagin guarantee that there exists a quadratic extension
![]() $K/{\mathbb Q}$
with the desired properties, it is not easy to determine all the primes that ramify in K. Using the proof of Matsuno as our inspiration, combined with more recent results of K. Ono, we prove an effective version of the theorem in Section 5.1.3. Assuming Goldfeld’s conjecture, we prove an effective version using simpler arguments in Section 5.1.2.
$K/{\mathbb Q}$
with the desired properties, it is not easy to determine all the primes that ramify in K. Using the proof of Matsuno as our inspiration, combined with more recent results of K. Ono, we prove an effective version of the theorem in Section 5.1.3. Assuming Goldfeld’s conjecture, we prove an effective version using simpler arguments in Section 5.1.2.
5.1.2 Effective version conditional on Goldfeld’s conjecture
Let us begin by reminding the reader of Goldfeld’s conjecture. This conjecture predicts that given an elliptic curve,
![]() $50\%$
of the quadratic twists have rank 0 and
$50\%$
of the quadratic twists have rank 0 and
![]() $50\%$
of the quadratic twists have rank 1. Therefore, if Goldfeld’s conjecture is true, then for
$50\%$
of the quadratic twists have rank 1. Therefore, if Goldfeld’s conjecture is true, then for
![]() $100\%$
of the time, the Mordell–Weil rank of
$100\%$
of the time, the Mordell–Weil rank of
![]() $E^{\prime }({\mathbb Q})$
is either 0 or 1, where
$E^{\prime }({\mathbb Q})$
is either 0 or 1, where
![]() $E^{\prime }$
is the quadratic twist of E (corresponding to a quadratic field K). Since
$E^{\prime }$
is the quadratic twist of E (corresponding to a quadratic field K). Since
for
![]() $100\%$
of the time,
$100\%$
of the time,
![]() $\operatorname {\mathrm {rank}}_{{\mathbb Z}}(E(K))=\operatorname {\mathrm {rank}}_{{\mathbb Z}}(E({\mathbb Q}))$
or
$\operatorname {\mathrm {rank}}_{{\mathbb Z}}(E(K))=\operatorname {\mathrm {rank}}_{{\mathbb Z}}(E({\mathbb Q}))$
or
![]() $\operatorname {\mathrm {rank}}_{{\mathbb Z}}(E(K))=\operatorname {\mathrm {rank}}_{{\mathbb Z}}(E({\mathbb Q}))+1$
. Suppose that the primes
$\operatorname {\mathrm {rank}}_{{\mathbb Z}}(E(K))=\operatorname {\mathrm {rank}}_{{\mathbb Z}}(E({\mathbb Q}))+1$
. Suppose that the primes
![]() $\ell _1, \ldots , \ell _k$
are chosen as in Matsuno’s theorem. These are primes of good ordinary reduction that lie in
$\ell _1, \ldots , \ell _k$
are chosen as in Matsuno’s theorem. These are primes of good ordinary reduction that lie in
![]() $T_{E/K}$
. Therefore, it follows from Lemma 5.3 that
$T_{E/K}$
. Therefore, it follows from Lemma 5.3 that
Using the Kummer sequence, we see that for
![]() $100\%$
of the quadratic fields K,
$100\%$
of the quadratic fields K,

Given
![]() $E_{/{\mathbb Q}}$
of conductor N and
$E_{/{\mathbb Q}}$
of conductor N and
![]() $n\in {\mathbb Z}_{\geq 0}$
, we want to find an imaginary quadratic field
$n\in {\mathbb Z}_{\geq 0}$
, we want to find an imaginary quadratic field
![]() $K/{\mathbb Q}$
with minimal conductor
$K/{\mathbb Q}$
with minimal conductor
![]() $\mathfrak {f}_{K}$
such that we can guarantee
$\mathfrak {f}_{K}$
such that we can guarantee
. Let
![]() $\mathcal {P} = \{\ell _1, \ldots , \ell _k\}$
be a set of (distinct) rational primes not dividing N, with the additional property that they split completely in
$\mathcal {P} = \{\ell _1, \ldots , \ell _k\}$
be a set of (distinct) rational primes not dividing N, with the additional property that they split completely in
![]() ${\mathbb Q}(E[2])/{\mathbb Q}$
and that precisely the primes in
${\mathbb Q}(E[2])/{\mathbb Q}$
and that precisely the primes in
![]() $\mathcal {P}$
ramify in K. From Equation (5-1), we need that
$\mathcal {P}$
ramify in K. From Equation (5-1), we need that
Equivalently,
Note that this inequality ensures that k can take all but finitely many values. Therefore, in view of Goldfeld’s conjecture, there exists a nonnegative integer
![]() $\epsilon _E$
such that the set
$\epsilon _E$
such that the set
![]() $\mathcal {P}$
contains
$\mathcal {P}$
contains
![]() $k+\epsilon _{E}$
(which we still call k by abuse of notation) many primes instead. To answer our question, we need to carefully pick the distinct primes
$k+\epsilon _{E}$
(which we still call k by abuse of notation) many primes instead. To answer our question, we need to carefully pick the distinct primes
![]() $\ell _1, \ldots , \ell _k$
. Given any integer M, the number of distinct prime factors denoted by
$\ell _1, \ldots , \ell _k$
. Given any integer M, the number of distinct prime factors denoted by
![]() $\omega (M)$
is asymptotically
$\omega (M)$
is asymptotically
![]() $\log \log M$
. Recall that the prime number theorem asserts that the average gap between consecutive primes among the first x many primes is
$\log \log M$
. Recall that the prime number theorem asserts that the average gap between consecutive primes among the first x many primes is
![]() $\log x$
. Since
$\log x$
. Since
![]() $\ell _1$
is a prime of good reduction,
$\ell _1$
is a prime of good reduction,
![]() $\ell _1\nmid N$
. The prime number theorem implies that
$\ell _1\nmid N$
. The prime number theorem implies that
![]() $\ell _1 \sim \log ( \omega (N)) \sim \log _{(3)} (N)$
. However, we need to do more. We require that
$\ell _1 \sim \log ( \omega (N)) \sim \log _{(3)} (N)$
. However, we need to do more. We require that
![]() $\ell _1$
splits completely in
$\ell _1$
splits completely in
![]() ${\mathbb Q}(E[2])/{\mathbb Q}$
. Using the Chebotarev density theorem, we can conclude that
${\mathbb Q}(E[2])/{\mathbb Q}$
. Using the Chebotarev density theorem, we can conclude that
![]() $\ell _1 \sim c \cdot \log \, ( \omega (N))$
, where c is either
$\ell _1 \sim c \cdot \log \, ( \omega (N))$
, where c is either
![]() $2$
,
$2$
,
![]() $3$
, or
$3$
, or
![]() $6$
depending on the degree of the Galois extension
$6$
depending on the degree of the Galois extension
![]() ${\mathbb Q}(E[2])/{\mathbb Q}$
. Of course, asymptotically,
${\mathbb Q}(E[2])/{\mathbb Q}$
. Of course, asymptotically,
![]() $\ell _1 \sim \log \, ( \omega (N))$
. Next,
$\ell _1 \sim \log \, ( \omega (N))$
. Next,
![]() $\ell _2 \nmid N\ell _1$
and splits completely in
$\ell _2 \nmid N\ell _1$
and splits completely in
![]() ${\mathbb Q}(E[2])/{\mathbb Q}$
. Note that the number of distinct prime divisors of
${\mathbb Q}(E[2])/{\mathbb Q}$
. Note that the number of distinct prime divisors of
![]() $N\ell _1 \sim \omega (N)+ 1$
. Using the same argument, we see that
$N\ell _1 \sim \omega (N)+ 1$
. Using the same argument, we see that
![]() $\ell _2 \sim \log \,( \omega (N) + 1)$
. Continuing this process,
$\ell _2 \sim \log \,( \omega (N) + 1)$
. Continuing this process,
 $$ \begin{align} \mathfrak{f} = \prod_{i=1}^k \ell_i &\sim \prod_{i=1}^k( \log (\omega(N) + (i-1))) \nonumber\\ &\sim \frac{(\log (\omega(N)-1+k))^{\omega(N)+2+k}}{\exp \operatorname{\mathrm{li}}(\omega(N)-1+k)} \nonumber\\ &\sim \frac{(\log n)^{n+c}}{\exp \operatorname{\mathrm{li}}(n)}, \end{align} $$
$$ \begin{align} \mathfrak{f} = \prod_{i=1}^k \ell_i &\sim \prod_{i=1}^k( \log (\omega(N) + (i-1))) \nonumber\\ &\sim \frac{(\log (\omega(N)-1+k))^{\omega(N)+2+k}}{\exp \operatorname{\mathrm{li}}(\omega(N)-1+k)} \nonumber\\ &\sim \frac{(\log n)^{n+c}}{\exp \operatorname{\mathrm{li}}(n)}, \end{align} $$
where
![]() $\operatorname {\mathrm {li}}(x) := \int _0^x ({dt}/{\log t})$
is the logarithmic integral and c is a constant depending on E. Let us explain the above estimates in greater detail. Setting
$\operatorname {\mathrm {li}}(x) := \int _0^x ({dt}/{\log t})$
is the logarithmic integral and c is a constant depending on E. Let us explain the above estimates in greater detail. Setting
 $$ \begin{align*} P(k):= \prod_{i=1}^k \log (\omega(N)+(i-1)), \end{align*} $$
$$ \begin{align*} P(k):= \prod_{i=1}^k \log (\omega(N)+(i-1)), \end{align*} $$
we wish to estimate the sum
 $$ \begin{align*} \log(P(k))= \sum_{i=1}^k \log (\log (\omega(N)+(i-1))). \end{align*} $$
$$ \begin{align*} \log(P(k))= \sum_{i=1}^k \log (\log (\omega(N)+(i-1))). \end{align*} $$
Using Abel’s partial summation formula (see for example [Reference ApostolApo76, Theorem 4.2]) with
![]() $f(t) = \log (\log (\omega (N) - 1 + t))$
,
$f(t) = \log (\log (\omega (N) - 1 + t))$
,
![]() $a(n) = 1$
, and
$a(n) = 1$
, and
![]() $A(x) = \sum _{n\leq x}a(n)$
,
$A(x) = \sum _{n\leq x}a(n)$
,
 $$ \begin{align*} &\log P(k)\\ &\quad= \sum_{i=1}^k \log\log(\omega(N) - 1 + i)\\&\quad= k \log\log(\omega(N) - 1 + k) - \int_0^k \frac{\lfloor x \rfloor}{(\omega(N) - 1 + x)\log(\omega(N) - 1 + x)}\, dx \\&\quad= k \log\log(\omega(N) - 1 + k) - \int_0^k \frac{x}{(\omega(N) - 1 + x)\log(\omega(N) - 1 + x)}\, dx \\& \qquad+ O\bigg( \int_0^k \frac{dx}{(\omega(N) - 1 + x)\log(\omega(N) - 1 + x)}\bigg) \\&\quad= k \log\log(\omega(N) - 1 + k) - ( \operatorname{\mathrm{li}}(\omega(N) - 1 + x) - (\omega(N) - 1)\log\log(\omega(N) - 1 + x) )|_0^k \\ & \qquad + O\bigg( \int_0^k \frac{dx}{(\omega(N) - 1 + x)\log(\omega(N) - 1 + x)}\bigg) \\ &\quad= k \log\log(\omega(N) - 1 + k) - \operatorname{\mathrm{li}}(\omega(N) - 1 + k) + (\omega(N) - 1)\log\log(\omega(N) - 1 + k) \\ & \qquad + O(\log\log(\omega(N) - 1 + k)) \\ &\quad= (k + \omega(N) + 1)\log\log(\omega(N) - 1 + k) - \operatorname{\mathrm{li}}(\omega(N) - 1 + k)\\ & \qquad + O(\log\log(\omega(N) - 1 + k)). \end{align*} $$
$$ \begin{align*} &\log P(k)\\ &\quad= \sum_{i=1}^k \log\log(\omega(N) - 1 + i)\\&\quad= k \log\log(\omega(N) - 1 + k) - \int_0^k \frac{\lfloor x \rfloor}{(\omega(N) - 1 + x)\log(\omega(N) - 1 + x)}\, dx \\&\quad= k \log\log(\omega(N) - 1 + k) - \int_0^k \frac{x}{(\omega(N) - 1 + x)\log(\omega(N) - 1 + x)}\, dx \\& \qquad+ O\bigg( \int_0^k \frac{dx}{(\omega(N) - 1 + x)\log(\omega(N) - 1 + x)}\bigg) \\&\quad= k \log\log(\omega(N) - 1 + k) - ( \operatorname{\mathrm{li}}(\omega(N) - 1 + x) - (\omega(N) - 1)\log\log(\omega(N) - 1 + x) )|_0^k \\ & \qquad + O\bigg( \int_0^k \frac{dx}{(\omega(N) - 1 + x)\log(\omega(N) - 1 + x)}\bigg) \\ &\quad= k \log\log(\omega(N) - 1 + k) - \operatorname{\mathrm{li}}(\omega(N) - 1 + k) + (\omega(N) - 1)\log\log(\omega(N) - 1 + k) \\ & \qquad + O(\log\log(\omega(N) - 1 + k)) \\ &\quad= (k + \omega(N) + 1)\log\log(\omega(N) - 1 + k) - \operatorname{\mathrm{li}}(\omega(N) - 1 + k)\\ & \qquad + O(\log\log(\omega(N) - 1 + k)). \end{align*} $$
This tells us that
 $$ \begin{align*} P(k) &= \exp((k + \omega(N) + 1)\log\log(\omega(N) - 1 + k) - \operatorname{\mathrm{li}}(\omega(N) - 1 + k)\\ & \quad + O(\log\log(\omega(N) - 1 + k)))\\ &= \frac{\exp((k + \omega(N) + 1)\log\log(\omega(N) - 1 + k))}{\exp( \operatorname{\mathrm{li}}(\omega(N) - 1 + k))}( \exp(O(\log\log(\omega(N) - 1 + k)))) \\ &= \frac{\exp((k + \omega(N) + 1)\log\log(\omega(N) - 1 + k))}{\exp( \operatorname{\mathrm{li}}(\omega(N) - 1 + k))}( O(\log(\omega(N) - 1 + k))) \\ &= \frac{\log(\omega(N) - 1 + k)^{k + \omega(N) + 2}}{\exp( \operatorname{\mathrm{li}}(\omega(N) - 1 + k))}. \end{align*} $$
$$ \begin{align*} P(k) &= \exp((k + \omega(N) + 1)\log\log(\omega(N) - 1 + k) - \operatorname{\mathrm{li}}(\omega(N) - 1 + k)\\ & \quad + O(\log\log(\omega(N) - 1 + k)))\\ &= \frac{\exp((k + \omega(N) + 1)\log\log(\omega(N) - 1 + k))}{\exp( \operatorname{\mathrm{li}}(\omega(N) - 1 + k))}( \exp(O(\log\log(\omega(N) - 1 + k)))) \\ &= \frac{\exp((k + \omega(N) + 1)\log\log(\omega(N) - 1 + k))}{\exp( \operatorname{\mathrm{li}}(\omega(N) - 1 + k))}( O(\log(\omega(N) - 1 + k))) \\ &= \frac{\log(\omega(N) - 1 + k)^{k + \omega(N) + 2}}{\exp( \operatorname{\mathrm{li}}(\omega(N) - 1 + k))}. \end{align*} $$
To obtain Equation (5-2), we note that for the given n, the difference between n and k depends on the rank of E, and further
![]() $\omega (N)$
depends on E. Thus, we can rewrite
$\omega (N)$
depends on E. Thus, we can rewrite
![]() $\omega (N)+2+k$
as
$\omega (N)+2+k$
as
![]() $n+c$
, where c is a constant depending only on the elliptic curve E.
$n+c$
, where c is a constant depending only on the elliptic curve E.
We have therefore proven the following result.
Theorem 5.6. Suppose that Goldfeld’s conjecture is true. Given an elliptic curve
![]() $E_{/{\mathbb Q}}$
and a positive integer n, there exists a quadratic extension
$E_{/{\mathbb Q}}$
and a positive integer n, there exists a quadratic extension
![]() $K/{\mathbb Q}$
with conductor
$K/{\mathbb Q}$
with conductor
![]() $\mathfrak {f}_K \sim {(\log n)^{n+c}}/{\exp \operatorname {\mathrm {li}} (n)}$
such that
$\mathfrak {f}_K \sim {(\log n)^{n+c}}/{\exp \operatorname {\mathrm {li}} (n)}$
such that
![]() . Here, c is an explicit constant depending only on E.
. Here, c is an explicit constant depending only on E.
Using a result of Ono, we can prove an unconditional statement which we now explain.
5.1.3 An unconditional effective version
Given an elliptic curve
![]() $E_{/{\mathbb Q}}$
of conductor N and a positive integer n, we want to find an imaginary quadratic field
$E_{/{\mathbb Q}}$
of conductor N and a positive integer n, we want to find an imaginary quadratic field
![]() $K/{\mathbb Q}$
with minimal conductor
$K/{\mathbb Q}$
with minimal conductor
![]() $\mathfrak {f}_{K}$
such that we can guarantee
$\mathfrak {f}_{K}$
such that we can guarantee
![]() .
.
For this section, we consider elliptic curves
![]() $E_{/{\mathbb Q}}$
that have no exceptional primes p, that is, no primes p such that the
$E_{/{\mathbb Q}}$
that have no exceptional primes p, that is, no primes p such that the
![]() $\mod p$
Galois representation attached to E is nonsurjective. This condition is a mild one: W. Duke has shown in [Reference DukeDuk97, Theorem 1] that almost all elliptic curves defined over
$\mod p$
Galois representation attached to E is nonsurjective. This condition is a mild one: W. Duke has shown in [Reference DukeDuk97, Theorem 1] that almost all elliptic curves defined over
![]() ${\mathbb Q}$
have no exceptional primes.
${\mathbb Q}$
have no exceptional primes.
For such elliptic curves
![]() $E_{/{\mathbb Q}}$
, [Reference OnoOno01, Theorem 1] asserts that there exists a fundamental discriminant
$E_{/{\mathbb Q}}$
, [Reference OnoOno01, Theorem 1] asserts that there exists a fundamental discriminant
![]() $D_E$
such that the twisted curve
$D_E$
such that the twisted curve
![]() $E^{d}$
has rank
$E^{d}$
has rank
![]() $0$
, where
$0$
, where
![]() $d = D_E\ell _1\cdots \ell _{k}$
for some even integer k and where the primes
$d = D_E\ell _1\cdots \ell _{k}$
for some even integer k and where the primes
![]() $\ell _i$
are chosen from a set (of primes) with density
$\ell _i$
are chosen from a set (of primes) with density
![]() $1$
. Indeed, the aforementioned theorem asserts (more generally) that there is a set of primes (call it S) with positive Frobenius density (that is, there exists a finite Galois extension
$1$
. Indeed, the aforementioned theorem asserts (more generally) that there is a set of primes (call it S) with positive Frobenius density (that is, there exists a finite Galois extension
![]() $L/{\mathbb Q}$
such that for all but finitely many primes in this set, these primes represent a fixed Frobenius conjugacy class in
$L/{\mathbb Q}$
such that for all but finitely many primes in this set, these primes represent a fixed Frobenius conjugacy class in
![]() $\operatorname {\mathrm {Gal}}(L/{\mathbb Q})$
) such that
$\operatorname {\mathrm {Gal}}(L/{\mathbb Q})$
) such that
![]() $E^{d}$
has rank
$E^{d}$
has rank
![]() $0$
, where
$0$
, where
![]() $d = D_E\ell _1\cdots \ell _{k}$
for some even integer k and the primes
$d = D_E\ell _1\cdots \ell _{k}$
for some even integer k and the primes
![]() $\ell _i$
are chosen from S. However, it follows from [Reference OnoOno01, proof of Theorem 2.2] that the field
$\ell _i$
are chosen from S. However, it follows from [Reference OnoOno01, proof of Theorem 2.2] that the field
![]() $L/{\mathbb Q}$
in the definition of the Frobenius density is the field that contains the coefficients of the newform associated to E. Since the elliptic curves we are working with are defined over
$L/{\mathbb Q}$
in the definition of the Frobenius density is the field that contains the coefficients of the newform associated to E. Since the elliptic curves we are working with are defined over
![]() ${\mathbb Q}$
, it follows from the modularity theorem that the newform will have integral coefficients, that is,
${\mathbb Q}$
, it follows from the modularity theorem that the newform will have integral coefficients, that is,
![]() $L = {\mathbb Q}$
. Since there is only one Frobenius class in
$L = {\mathbb Q}$
. Since there is only one Frobenius class in
![]() ${\mathbb Q}$
, namely the trivial class, [Reference OnoOno01, Theorem 1] says that the density of the set S is
${\mathbb Q}$
, namely the trivial class, [Reference OnoOno01, Theorem 1] says that the density of the set S is
![]() $1$
.
$1$
.
Let K be the quadratic field associated with the twist d. Since
![]() $E^d$
has rank 0, we know that
$E^d$
has rank 0, we know that
![]() $\operatorname {\mathrm {rank}}_{{\mathbb Z}}(E(K))=\operatorname {\mathrm {rank}}_{{\mathbb Z}}(E({\mathbb Q}))$
. It follows that
$\operatorname {\mathrm {rank}}_{{\mathbb Z}}(E(K))=\operatorname {\mathrm {rank}}_{{\mathbb Z}}(E({\mathbb Q}))$
. It follows that
If K is a quadratic field arising from Ono’s theorem such that
, it is required that
To answer our question, we pick the distinct primes
![]() $\ell _1, \ldots , \ell _k$
using the exact same process as before. We have that
$\ell _1, \ldots , \ell _k$
using the exact same process as before. We have that
 $$ \begin{align*} \mathfrak{f} = D_E\prod_{i=1}^k \ell_i \sim \prod_{i=1}^k( \log (\omega(N) + (i-1))) \sim \frac{(\log (\omega(N)+k))^{\omega(N)+k}}{\exp \operatorname{\mathrm{li}}(\omega(N)+k)} \sim \frac{(\log n)^{n+c}}{\exp \operatorname{\mathrm{li}}(n)},\end{align*} $$
$$ \begin{align*} \mathfrak{f} = D_E\prod_{i=1}^k \ell_i \sim \prod_{i=1}^k( \log (\omega(N) + (i-1))) \sim \frac{(\log (\omega(N)+k))^{\omega(N)+k}}{\exp \operatorname{\mathrm{li}}(\omega(N)+k)} \sim \frac{(\log n)^{n+c}}{\exp \operatorname{\mathrm{li}}(n)},\end{align*} $$
where
![]() $\operatorname {\mathrm {li}}(x) := \int _0^x ({dt}/{\log t})$
is the logarithmic integral and c is a constant depending on E.
$\operatorname {\mathrm {li}}(x) := \int _0^x ({dt}/{\log t})$
is the logarithmic integral and c is a constant depending on E.
We have therefore proven the following result.
Theorem 5.7. Given an elliptic curve
![]() $E_{/{\mathbb Q}}$
with no exceptional primes and a positive integer n, there exists a quadratic extension
$E_{/{\mathbb Q}}$
with no exceptional primes and a positive integer n, there exists a quadratic extension
![]() $K/{\mathbb Q}$
with conductor
$K/{\mathbb Q}$
with conductor
![]() $\mathfrak {f}_K \sim {(\log n)^{n+c}}/{\exp \operatorname {\mathrm {li}} (n)}$
such that
$\mathfrak {f}_K \sim {(\log n)^{n+c}}/{\exp \operatorname {\mathrm {li}} (n)}$
such that
![]() . Here, c is an explicit constant depending only on E.
. Here, c is an explicit constant depending only on E.
5.2 Arbitrarily large
 in
in
 ${\mathbb Z}/p{\mathbb Z}$
-extensions
${\mathbb Z}/p{\mathbb Z}$
-extensions
Let
![]() $E_{/{\mathbb Q}}$
be a fixed rank 0 elliptic curve of conductor N. Let p be a fixed odd prime. Let F be any number field. We have the obvious short exact sequence
$E_{/{\mathbb Q}}$
be a fixed rank 0 elliptic curve of conductor N. Let p be a fixed odd prime. Let F be any number field. We have the obvious short exact sequence
It follows that
When
![]() $F/{\mathbb Q}$
is a cyclic degree-p Galois extension, we know from Lemma 5.3 that
$F/{\mathbb Q}$
is a cyclic degree-p Galois extension, we know from Lemma 5.3 that
Given an integer n, there exists a number field
![]() $F_{(n)}$
such that (see [Reference ČesnavičiusČes17, Theorem 1.2])
$F_{(n)}$
such that (see [Reference ČesnavičiusČes17, Theorem 1.2])
Denote the conductor of
![]() $F_{(n)}$
by
$F_{(n)}$
by
![]() $\mathfrak {f}(F_{(n)})$
. Varying over all
$\mathfrak {f}(F_{(n)})$
. Varying over all
![]() ${\mathbb Z}/p{\mathbb Z}$
-extensions of
${\mathbb Z}/p{\mathbb Z}$
-extensions of
![]() ${\mathbb Q}$
, there are infinitely many number fields
${\mathbb Q}$
, there are infinitely many number fields
![]() $L/{\mathbb Q}$
such that
$L/{\mathbb Q}$
such that
![]() $T_{E/L} \supseteq T_{E/F_{(n)}}$
, that is,
$T_{E/L} \supseteq T_{E/F_{(n)}}$
, that is,
![]() $\mathfrak {f}(F_{(n)})\mid \mathfrak {f}(L)$
. For each such L,
$\mathfrak {f}(F_{(n)})\mid \mathfrak {f}(L)$
. For each such L,
Recall the conjecture of David, Fearnley, and Kisilevsky from Section 2. If
![]() $p\geq 7$
, it predicts the boundedness of the set
$p\geq 7$
, it predicts the boundedness of the set
If this conjecture is true, then varying over all
![]() ${\mathbb Z}/p{\mathbb Z}$
-extensions of
${\mathbb Z}/p{\mathbb Z}$
-extensions of
![]() ${\mathbb Q}$
, there are only finitely many cyclic p-extensions
${\mathbb Q}$
, there are only finitely many cyclic p-extensions
![]() $L/{\mathbb Q}$
in which there is a rank jump upon base-change. Therefore, given an integer n, one can find an integer
$L/{\mathbb Q}$
in which there is a rank jump upon base-change. Therefore, given an integer n, one can find an integer
![]() $M = M(n)$
and a number field
$M = M(n)$
and a number field
![]() $L/{\mathbb Q}$
such that:
$L/{\mathbb Q}$
such that:
-
(i)
 $\mathfrak {f}(L)> M(n)$
;
$\mathfrak {f}(L)> M(n)$
; -
(ii)
 $\mathfrak {f}(F_{(n)})\mid \mathfrak {f}(L)$
;
$\mathfrak {f}(F_{(n)})\mid \mathfrak {f}(L)$
; -
(iii)
 $\operatorname {\mathrm {rank}}_{{\mathbb Z}}(E(L)) = \operatorname {\mathrm {rank}}_{{\mathbb Z}}(E({\mathbb Q}))$
.
$\operatorname {\mathrm {rank}}_{{\mathbb Z}}(E(L)) = \operatorname {\mathrm {rank}}_{{\mathbb Z}}(E({\mathbb Q}))$
.
Thus, given n, there exists a cyclic extension
![]() $L/{\mathbb Q}$
of degree
$L/{\mathbb Q}$
of degree
![]() $p\geq 7$
such that Equation (5-3) becomes
$p\geq 7$
such that Equation (5-3) becomes
Since
![]() $\operatorname {\mathrm {rank}}_{{\mathbb Z}}(E({\mathbb Q}))$
is independent of L and
$\operatorname {\mathrm {rank}}_{{\mathbb Z}}(E({\mathbb Q}))$
is independent of L and
![]() $\operatorname {\mathrm {rank}}_p E(L)[p]$
is at most 2, it means that given n, there exists a
$\operatorname {\mathrm {rank}}_p E(L)[p]$
is at most 2, it means that given n, there exists a
![]() ${\mathbb Z}/p{\mathbb Z}$
-extension
${\mathbb Z}/p{\mathbb Z}$
-extension
![]() $L/{\mathbb Q}$
such that
$L/{\mathbb Q}$
such that
.
We feel that the full force of the conjecture of David, Fearnley, and Kisilevsky is required. In particular, we do not see if the result of Mazur and Rubin is sufficient. This is because it is not obvious to us as to why, even if there are infinitely many number fields
![]() $\mathcal {L}/{\mathbb Q}$
with
$\mathcal {L}/{\mathbb Q}$
with
![]() $\operatorname {\mathrm {rank}}_{{\mathbb Z}}(E(\mathcal {L})) = \operatorname {\mathrm {rank}}_{{\mathbb Z}}(E(\mathcal {{\mathbb Q}}))$
, there should be any (of these) satisfying
$\operatorname {\mathrm {rank}}_{{\mathbb Z}}(E(\mathcal {L})) = \operatorname {\mathrm {rank}}_{{\mathbb Z}}(E(\mathcal {{\mathbb Q}}))$
, there should be any (of these) satisfying
![]() $\mathfrak {f}({F_{(n)}})\mid \mathfrak {f}(\mathcal {L})$
.
$\mathfrak {f}({F_{(n)}})\mid \mathfrak {f}(\mathcal {L})$
.
6 Tables
6.1. In Table 1, we compute the following expression:
 $$ \begin{align*} \bigg(1 - \frac{1}{p}\bigg) \bigg( 1 - \prod_{q \equiv 1 (\textrm{mod }{p})} \bigg( \frac{q-1}{2q^2} + 1 - \frac{1}{q}\bigg) \bigg) \end{align*} $$
$$ \begin{align*} \bigg(1 - \frac{1}{p}\bigg) \bigg( 1 - \prod_{q \equiv 1 (\textrm{mod }{p})} \bigg( \frac{q-1}{2q^2} + 1 - \frac{1}{q}\bigg) \bigg) \end{align*} $$
for
![]() $3\leq p < 50$
and
$3\leq p < 50$
and
![]() $q \leq 179\,424\,673$
(that is, the first 10 million primes).
$q \leq 179\,424\,673$
(that is, the first 10 million primes).
6.2. In Table 2, we record the proportion of enemy primes for CM elliptic curves with conductor
![]() $<100$
and
$<100$
and
![]() $p<50$
. Here, ‘–’ indicates that for a given elliptic curve, p is an irrelevant prime. Since
$p<50$
. Here, ‘–’ indicates that for a given elliptic curve, p is an irrelevant prime. Since
![]() $p=47$
is an irrelevant prime for the four elliptic curves of interest, we have excluded it from our table. In the first row, the value of
$p=47$
is an irrelevant prime for the four elliptic curves of interest, we have excluded it from our table. In the first row, the value of
![]() ${p}/{2(p+1)(p-1)^2}$
is recorded. Note that the reduction type depends only on the isogeny class. The same is true for the
${p}/{2(p+1)(p-1)^2}$
is recorded. Note that the reduction type depends only on the isogeny class. The same is true for the
![]() $\lambda $
-invariant of the p-primary Selmer group. However, it is possible that one or more of the curves in a given isogeny class has positive
$\lambda $
-invariant of the p-primary Selmer group. However, it is possible that one or more of the curves in a given isogeny class has positive
![]() $\mu $
-invariant, but the others do not (see also [Reference Greenberg and ViolaGre99, Conjecture 1.11]). To keep the tables succinct, since the Iwasawa invariants are the same for all curves in the isogeny class, they are clubbed together.
$\mu $
-invariant, but the others do not (see also [Reference Greenberg and ViolaGre99, Conjecture 1.11]). To keep the tables succinct, since the Iwasawa invariants are the same for all curves in the isogeny class, they are clubbed together.
The data in the table are obtained from the code available here.
Acknowledgements
LB and DK thank Rahul Arora, Christopher Keyes, Debasis Kundu, Allysa Lumley, Jackson Morrow, Kumar Murty, Mohammed Sadek, and Frank Thorne for helpful discussions during the preparation of this article. LB and DK thank Henri Darmon for his continued support. This work was initiated by LB and DK during the thematic semester ‘Number Theory – Cohomology in Arithmetic’ at Centre de Recherches Mathématiques (CRM) in Fall 2020. LB and DK thank the CRM for the hospitality and generous support. AR thanks Ravi Ramakrishna, R. Sujatha, and Tom Weston for their support and guidance, and thanks Larry Washington for helpful conversations. We thank Henri Darmon, Chantal David, Antonio Lei, Robert Lemke Oliver, Jackson Morrow, Ross Paterson, Ravi Ramakrishna, and Larry Washington for their comments on an earlier draft of this paper. We thank the referee for the timely review and for the suggestions that led to various improvements in the exposition.