Hostname: page-component-8448b6f56d-tj2md Total loading time: 0 Render date: 2024-04-23T20:25:44.966Z Has data issue: false hasContentIssue false
  • English
  • Français

THE PARTIAL-ISOMETRIC CROSSED PRODUCTS BY SEMIGROUPS OF ENDOMORPHISMS AS FULL CORNERS

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  01 April 2014

SRIWULAN ADJI  and
SAEID ZAHMATKESH
SRIWULAN ADJI*
Affiliation:
Institute of Mathematical Sciences. University Malaya, Kuala Lumpur, Malaysia
SAEID ZAHMATKESH
Affiliation:
School of Mathematical Sciences, Universiti Sains Malaysia, Penang, Malaysia email zahmatkesh.s@gmail.com
*
✉sriwulan.adji@yahoo.com,sriwulan.adji@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose that 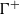${\Gamma }^{+ } $ is the positive cone of a totally ordered abelian group 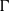$\Gamma $, and 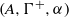$(A, {\Gamma }^{+ } , \alpha )$ is a system consisting of a 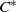${C}^{\ast } $-algebra 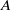$A$, an action $\alpha $ of 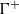${\Gamma }^{+ } $ by extendible endomorphisms of 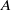$A$. We prove that the partial-isometric crossed product 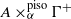$A\hspace{0.167em} { \mathop{\times }\nolimits}_{\alpha }^{\mathrm{piso} } \hspace{0.167em} {\Gamma }^{+ } $ is a full corner in the subalgebra of 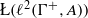$\L ({\ell }^{2} ({\Gamma }^{+ } , A))$, and that if $\alpha $ is an action by automorphisms of 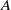$A$, then it is the isometric crossed product 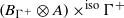$({B}_{{\Gamma }^{+ } } \otimes A)\hspace{0.167em} {\mathop{\times }\nolimits }^{\mathrm{iso} } \hspace{0.167em} {\Gamma }^{+ } $, which is therefore a full corner in the usual crossed product of system by a group of automorphisms. We use these realizations to identify the ideal of 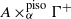$A\hspace{0.167em} { \mathop{\times }\nolimits}_{\alpha }^{\mathrm{piso} } \hspace{0.167em} {\Gamma }^{+ } $ such that the quotient is the isometric crossed product 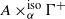$A\hspace{0.167em} { \mathop{\times }\nolimits}_{\alpha }^{\mathrm{iso} } \hspace{0.167em} {\Gamma }^{+ } $.

Keywords

C∗-algebraautomorphismendomorphismsemigrouppartial isometrycrossed product

MSC classification

Secondary: 46L55: Noncommutative dynamical systems
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 96 , Issue 2 , April 2014 , pp. 145 - 166
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Adji, S., Invariant ideals of crossed products by semigroups of endomorphisms, Proc. Conference in Functional Analysis and Global Analysis in Manila, October 1996 (Springer, Singapore 1996), 1–8.Google Scholar
Adji, S., ‘Semigroup crossed products and the structure of Toeplitz algebras’, J. Operator Theory 44 (2000), 139–150.Google Scholar
Adji, S., ‘A remark on semigroup crossed products’, Vietnam J. Math. 31 (4) (2003), 429–435.Google Scholar
Adji, S., Laca, M., Nilsen, M. and Raeburn, I., ‘Crossed products by semigroups of endomorphisms and the Toeplitz algebras of ordered groups’, Proc. Amer. Math. Soc. 122 (4) (1994), 1133–1141.Google Scholar
Adji, S. and Hosseini, A., ‘The partial-isometric crossed products of ${c}_{0} $ by the forward and backward shifts’, Bull. Malays. Math. Sci. Soc. (2) 33 (3) (2010), 487–498.Google Scholar
Fowler, N. J., ‘Discrete product systems of Hilbert bimodules’, Pacific J. Math. 204 (2002), 335–375.Google Scholar
Khoshkam, M. and Skandalis, G., ‘Toeplitz algebras associated with endomorphisms and Pimsner–Voiculescu exact sequences’, Pacific J. Math. 181 (2) (1997), 315–331.Google Scholar
Laca, M., ‘From endomorphisms to automorphisms and back: dilations and full corners’, J. London Math. Soc. 61 (2) (2000), 893–904.Google Scholar
Larsen, N. S., ‘Nonunital semigroup crossed products’, Math. Proc. R. Ir. Acad. 100A (2000), 205–218.Google Scholar
Lindiarni, J. and Raeburn, I., ‘Partial-isometric crossed products by semigroups of endomorphisms’, J. Operator Theory 52 (2004), 61–87.Google Scholar
Murphy, G. J., ‘Ordered groups and Toeplitz algebras’, J. Operator Theory 18 (1987), 303–326.Google Scholar
Murphy, G. J., ‘Ordered groups and crossed products of ${C}^{\ast } $-algebras’, Pacific J. Math. 148 (1991), 319–349.Google Scholar
Murphy, G. J., ‘Crossed products of ${C}^{\ast } $-algebras by semigroups of automorphisms’, Proc. London Math. Soc. 68 (3) (1994), 423–448.CrossRefGoogle Scholar
Pimsner, M. and Voiculescu, D., ‘Exact sequences for $K$-groups and Ext-groups of certain cross-product ${C}^{\ast } $-algebras’, J. Operator Theory 4 (1) (1980), 93–118.Google Scholar
Raeburn, I. and Williams, D. P., Morita Equivalence and Continuous-trace C∗-algebras, Mathematical Surveys and Monographs, 60 (American Mathematical Society, Providence, RI, 1998).Google Scholar
Stacey, P. J., ‘Crossed products of ${C}^{\ast } $-algebras by $\ast $-endomorphisms’, J. Aust. Math. Soc. Ser. A 54 (1993), 204–212.CrossRefGoogle Scholar
Williams, D. P., Crossed Products of C∗-Algebras, Mathematical Surveys and Monographs, 134 (American Mathematical Society, Providence, RI, 2007).CrossRefGoogle Scholar