Hostname: page-component-8448b6f56d-sxzjt Total loading time: 0 Render date: 2024-04-19T21:17:12.886Z Has data issue: false hasContentIssue false
  • English
  • Français

ORTHOGONALITY AND PARALLELISM OF OPERATORS ON VARIOUS BANACH SPACES

Part of: General theory of linear operators

Published online by Cambridge University Press:  22 August 2018

T. BOTTAZZI ,
C. CONDE ,
M. S. MOSLEHIAN ,
P. WÓJCIK  and
A. ZAMANI
T. BOTTAZZI
Affiliation:
Instituto Argentino de Matemática, ‘Alberto P. Calderón’, Saavedra 15 3o piso, (C1083ACA) Buenos Aires, Argentina email tpbottaz@ungs.edu.ar
C. CONDE
Affiliation:
Instituto Argentino de Matemática, ‘Alberto P. Calderón’, Saavedra 15 3o piso, (C1083ACA) Buenos Aires, Argentina Instituto de Ciencias, Universidad Nacional de General Sarmiento, J. M. Gutierrez 1150, (B1613GSX) Los Polvorines, Argentina email cconde@ungs.edu.ar
M. S. MOSLEHIAN*
Affiliation:
Department of Pure Mathematics, Ferdowsi University of Mashhad, P.O. Box 1159, Mashhad 91775, Iran email moslehian@um.ac.ir
P. WÓJCIK
Affiliation:
Institute of Mathematics, Pedagogical University of Cracow, Podchora̧żych 2, 30-084 Kraków, Poland email pwojcik@up.krakow.pl
A. ZAMANI
Affiliation:
Department of Mathematics, Farhangian University, Tehran, Iran email zamani.ali85@yahoo.com
*
✉moslehian@um.ac.ir
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

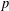We present some properties of orthogonality and relate them with support disjoint and norm inequalities in $p$-Schatten ideals. In addition, we investigate the problem of characterization of norm-parallelism for bounded linear operators. We consider the characterization of the norm-parallelism problem in 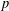$p$-Schatten ideals and locally uniformly convex spaces. Later on, we study the case when an operator is norm-parallel to the identity operator. Finally, we give some equivalence assertions about the norm-parallelism of compact operators. Some applications and generalizations are discussed for certain operators.

Keywords

orthogonality; norm-parallelism; Schatten p-norm; disjoint supports; trace; compact operator

MSC classification

Primary: 47A30: Norms (inequalities, more than one norm, etc.)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 106 , Issue 2 , April 2019 , pp. 160 - 183
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

The third author was supported by a grant from Ferdowsi University of Mashhad (no. 1/43523).

References

Abatzoglou, T. J., ‘Norm derivatives on spaces of operators’, Math. Ann. 239(2) (1979), 129–135.Google Scholar
Alonso, J., Martini, H. and Wu, S., ‘On Birkhoff orthogonality and isosceles orthogonality in normed linear spaces’, Aequationes Math. 83 (2012), 153–189.Google Scholar
Arazy, J., ‘The isometries of C p ’, Israel J. Math. 22(3–4) (1975), 247–256.Google Scholar
Benítez, C., Fernández, M. and Soriano, M. L., ‘Orthogonality of matrices’, Linear Algebra Appl. 422 (2007), 155–163.Google Scholar
Bhatia, R. and Šemrl, P., ‘Orthogonality of matrices and some distance problems’, Linear Algebra Appl. 287(1–3) (1999), 77–85.Google Scholar
Bhattacharyya, T. and Grover, P., ‘Characterization of Birkhoff–James orthogonality’, J. Math. Anal. Appl. 407(2) (2013), 350–358.Google Scholar
Birkhoff, G., ‘Orthogonality in linear metric spaces’, Duke Math. J. 1 (1935), 169–172.Google Scholar
Busch, P., ‘Stochastic isometries in quantum mechanics’, Math. Phys. Anal. Geom. 2(1) (1999), 83–106.Google Scholar
Chmieliński, J., ‘Operators reversing orthogonality in normed spaces’, Adv. Oper. Theory 1(1) (2016), 8–14.Google Scholar
Clarkson, J. A., ‘Uniformly convex spaces’, Trans. Amer. Math. Soc. 40(3) (1936), 396–414.Google Scholar
Dragomir, S. S., Semi-Inner Products and Applications (Nova Science, Hauppauge, NY, 2004).Google Scholar
Ghosh, P., Sain, D. and Paul, K., ‘On symmetry of Birkhoff–James orthogonality of linear operators’, Adv. Oper. Theory 2(4) (2017), 428–434.Google Scholar
Giles, J. R., ‘Classes of semi-inner-product spaces’, Trans. Amer. Math. Soc. 129 (1967), 436–446.Google Scholar
Gohberg, I. C. and Kreĭn, M. G., Introduction to the Theory of Linear Nonselfadjoint Operators, Translations of Mathematical Monographs, 18 (American Mathematical Society, Providence, RI, 1969), translated from the Russian by A. Feinstein.Google Scholar
Grover, P., ‘Orthogonality of matrices in the Ky Fan k-norms’, Linear Multilinear Algebra 65(3) (2017), 496–509.Google Scholar
James, R. C., ‘Orthogonality in normed linear spaces’, Duke Math. J. 12 (1945), 291–301.Google Scholar
James, R. C., ‘Orthogonality and linear functionals in normed linear spaces’, Trans. Amer. Math. Soc. 61 (1947), 265–292.Google Scholar
Kittaneh, F., ‘On zero-trace matrices’, Linear Algebra Appl. 151 (1991), 119–124.Google Scholar
Li, Y. and Li, Y.-E., ‘Some characterizations of the trace norm triangle equality’, Linear Algebra Appl. 484 (2015), 396–408.Google Scholar
Lumer, G., ‘Semi-inner-product spaces’, Trans. Amer. Math. Soc. 100 (1961), 29–43.Google Scholar
Magajna, B., ‘On the distance to finite-dimensional subspaces in operator algebras’, J. Lond. Math. Soc. (2) 47(3) (1993), 516–532.Google Scholar
Maher, P. J., ‘Some operator inequalities concerning generalized inverses’, Illinois J. Math. 34(3) (1990), 503–514.Google Scholar
Maher, P. J., ‘Some norm inequalities concerning generalized inverses’, Linear Algebra Appl. 174 (1992), 99–110.Google Scholar
Maligranda, L., ‘Some remarks on the triangle inequality for norms’, Banach J. Math. Anal. 2(2) (2008), 31–41.Google Scholar
McCarthy, C. A., ‘ c p ’, Israel J. Math. 5 (1967), 249–271.Google Scholar
Moslehian, M. S. and Zamani, A., ‘Characterizations of operator Birkhoff–James orthogonality’, Canad. Math. Bull. 60(4) (2017), 816–829.Google Scholar
Paul, K., Sain, D. and Ghosh, P., ‘Birkhoff–James orthogonality and smoothness of bounded linear operators’, Linear Algebra Appl. 506 (2016), 551–563.Google Scholar
Sain, D., ‘On the norm attainment set of a bounded linear operator’, J. Math. Anal. Appl. 457(1) (2018), 67–76.Google Scholar
Sain, D., Paul, K. and Hait, S., ‘Operator norm attainment and Birkhoff–James orthogonality’, Linear Algebra Appl. 476 (2015), 85–97.Google Scholar
Seddik, A., ‘Rank one operators and norm of elementary operators’, Linear Algebra Appl. 424 (2007), 177–183.Google Scholar
Stampfli, J. G., ‘The norm of a derivation’, Pacific J. Math. 33 (1970), 737–747.Google Scholar
Werner, D., ‘An elementary approach to the Daugavet equation’, in: Interaction Between Functional Analysis, Harmonic Analysis, and Probability (Columbia, MO, 1994), Lecture Notes in Pure and Applied Mathematics, 175 (Marcel Dekker, New York, 1996), 449–454.Google Scholar
Wójcik, P., ‘The Birkhoff orthogonality in pre-Hilbert C ∗ -modules’, Oper. Matrices 10(3) (2016), 713–729.Google Scholar
Wójcik, P., ‘Orthogonality of compact operators’, Expo. Math. 35(1) (2017), 86–94.Google Scholar
Wójcik, P., ‘Norm-parallelism in classical M-ideals’, Indag. Math. (N.S.) 28(2) (2017), 287–293.Google Scholar
Zamani, A., ‘The operator-valued parallelism’, Linear Algebra Appl. 505 (2016), 282–295.Google Scholar
Zamani, A. and Moslehian, M. S., ‘Exact and approximate operator parallelism’, Canad. Math. Bull. 58(1) (2015), 207–224.Google Scholar
Zamani, A. and Moslehian, M. S., ‘Norm-parallelism in the geometry of Hilbert C ∗ -modules’, Indag. Math. (N.S.) 27(1) (2016), 266–281.Google Scholar