Hostname: page-component-76fb5796d-22dnz Total loading time: 0 Render date: 2024-04-26T22:24:33.227Z Has data issue: false hasContentIssue false
  • English
  • Français

ON ODD-DIMENSIONAL COMPLEX ANALYTIC KLEINIAN GROUPS

Part of: Compact analytic spaces Riemann surfaces Geometric convexity Global differential geometry

Published online by Cambridge University Press:  12 February 2019

MASAHIDE KATO
MASAHIDE KATO*
Affiliation:
Sophia University, Kioicho 7-1, Chiyoda-ku, Tokyo 102-8554, Japan email masahide.kato@sophia.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

We shall explain here an idea to generalize classical complex analytic Kleinian group theory to any odd-dimensional cases. For a certain class of discrete subgroups of 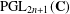$\text{PGL}_{2n+1}(\mathbf{C})$ acting on 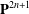$\mathbf{P}^{2n+1}$, we can define their domains of discontinuity in a canonical manner, regarding an $n$-dimensional projective linear subspace in 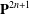$\mathbf{P}^{2n+1}$ as a point, like a point in the classical one-dimensional case. Many interesting (compact) non-Kähler manifolds appear systematically as the canonical quotients of the domains. In the last section, we shall give some examples.

Keywords

compact non-Kähler manifoldprojective structureKleinian group theory

MSC classification

Primary: 32J18: Compact $n$-folds
Secondary: 30F40: Kleinian groups 32F10: $q$-convexity, $q$-concavity 32F17: Other notions of convexity 53C56: Other complex differential geometry
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 108 , Issue 1 , February 2020 , pp. 1 - 32
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Campana, F., ‘Algébricité et compacité dans l’espace des cycles d’un espace analytique complexe’, Math. Ann. 251 (1980), 7–18.Google Scholar
Fujiki, A., ‘Compact non-Kähler threefolds associated to hyperbolic 3-manifolds’, Proceedings of Hayama Symposium on Complex Analysis in Several Complex Variables 2005, 1–4, December 18–21, Shonan Village, Japan.Google Scholar
Guillot, A., ‘Sur les équations d’Halphen et les action de SL2(C)’, Publ. Math. Inst. Hautes Études Sci. (105) (2007), 221–294.Google Scholar
Ivashkovich, S. M., ‘Extension of locally biholomorphic mappings of domains into a complex projective space’, Izv. Akad. Nauk SSSR Ser. Mat. 47 (1983), 197–206.Google Scholar
Kapovich, M., ‘Hyperbolic manifolds and discrete groups’, Modern Birkhäuser Classics (Birkhäuser, Boston–Basel–Berlin, 2001).Google Scholar
Kato, Ma., ‘On compact complex 3-folds with lines’, Japanese J. Math. 11 (1985), 1–58.Google Scholar
Kato, Ma., ‘Examples on an extension problem of holomorphic maps and a holomorphic 1-dimensional foliation’, Tokyo J. Math. 13 (1990), 139–146.Google Scholar
Kato, Ma., ‘Compact quotient manifolds of domains in a complex 3-dimensional projective space and the Lebesgue measure of limit sets’, Tokyo J. Math. 19 (1996), 99–119.Google Scholar
Kato, Ma., ‘Existence of invariant planes in a complex projective 3-space under discrete projective transformation groups’, Tokyo J. Math. 34 (2011), 261–285.Google Scholar
Lárusson, F., ‘Compact quotients of large domains in compact projective space’, Ann. Inst. Fourier Grenoble 48(1) (1998), 223–246.Google Scholar
Maskit, B., Kleinian Groups, Grundlehren der Mathematischen Wissenschaften, 287 (Springer, Berlin–Heidelberg, 1987).Google Scholar
Myrberg, P. J., ‘Untersuchungen über die Automorphen Funktionen Beliebig Vieler Variablen’, Acta Math. 46 (1925), 215–336.Google Scholar
Ueno, K., Classification Theory of Algebraic Varieties and Compact Complex Spaces, Lecture Notes in Mathematics, 439 (Springer, Berlin–Heidelberg, 1975).Google Scholar