Article contents
ON GRADED SYMMETRIC CELLULAR ALGEBRAS
Published online by Cambridge University Press: 29 July 2019
Abstract
Let  $A=\bigoplus _{i\in \mathbb{Z}}A_{i}$ be a finite-dimensional graded symmetric cellular algebra with a homogeneous symmetrizing trace of degree
$A=\bigoplus _{i\in \mathbb{Z}}A_{i}$ be a finite-dimensional graded symmetric cellular algebra with a homogeneous symmetrizing trace of degree 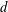 $d$. We prove that if
$d$. We prove that if 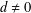 $d\neq 0$ then
$d\neq 0$ then 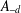 $A_{-d}$ contains the Higman ideal
$A_{-d}$ contains the Higman ideal 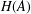 $H(A)$ and
$H(A)$ and 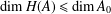 $\dim H(A)\leq \dim A_{0}$, and provide a semisimplicity criterion for
$\dim H(A)\leq \dim A_{0}$, and provide a semisimplicity criterion for 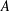 $A$ in terms of the centralizer of
$A$ in terms of the centralizer of 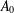 $A_{0}$.
$A_{0}$.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2019 Australian Mathematical Publishing Association Inc.
Footnotes
Li is supported by the Natural Science Foundation of Hebei Province, China (A2017501003) and the Science and Technology support program of Northeastern University at Qinhuangdao (No. XNK201601). Zhao is supported partly by NSFC 11571341, 11671234, 11871107.
References
- 1
- Cited by


