Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-26T10:38:51.468Z Has data issue: false hasContentIssue false
  • English
  • Français

ON A NEW CIRCLE PROBLEM

Part of: Multiplicative number theory

Published online by Cambridge University Press:  08 November 2016

JUN FURUYA ,
MAKOTO MINAMIDE  and
YOSHIO TANIGAWA
JUN FURUYA
Affiliation:
Department of Integrated Human Sciences (Mathematics), Hamamatsu University School of Medicine, Handayama 1-20-1, Hamamatsu, Shizuoka431-3192, Japan email jfuruya@hama-med.ac.jp
MAKOTO MINAMIDE*
Affiliation:
Faculty of Science, Yamaguchi University, Yoshida 1677-1, Yamaguchi 753-8512, Japan email minamide@yamaguchi-u.ac.jp
YOSHIO TANIGAWA
Affiliation:
Graduate School of Mathematics, Nagoya University, Furo-cho, Nagoya 464-8602, Japan email tanigawa@math.nagoya-u.ac.jp
*
✉minamide@yamaguchi-u.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We attempt to discuss a new circle problem. Let 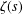$\unicode[STIX]{x1D701}(s)$ denote the Riemann zeta-function 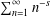$\sum _{n=1}^{\infty }n^{-s}$ (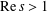$\text{Re}\,s>1$) and 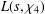$L(s,\unicode[STIX]{x1D712}_{4})$ the Dirichlet 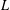$L$-function 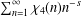$\sum _{n=1}^{\infty }\unicode[STIX]{x1D712}_{4}(n)n^{-s}$ (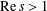$\text{Re}\,s>1$) with the primitive Dirichlet character mod 4. We shall define an arithmetical function 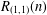$R_{(1,1)}(n)$ by the coefficient of the Dirichlet series 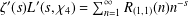$\unicode[STIX]{x1D701}^{\prime }(s)L^{\prime }(s,\unicode[STIX]{x1D712}_{4})=\sum _{n=1}^{\infty }R_{(1,1)}(n)n^{-s}$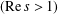$(\text{Re}\,s>1)$. This is an analogue of 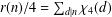$r(n)/4=\sum _{d|n}\unicode[STIX]{x1D712}_{4}(d)$. In the circle problem, there are many researches of estimations and related topics on the error term in the asymptotic formula for 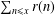$\sum _{n\leq x}r(n)$. As a new problem, we deduce a ‘truncated Voronoï formula’ for the error term in the asymptotic formula for 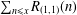$\sum _{n\leq x}R_{(1,1)}(n)$. As a direct application, we show the mean square for the error term in our new problem.

Keywords

the circle problemthe truncated Voronoï formuladerivatives of Riemann zeta- and Dirichlet L-functions

MSC classification

Primary: 11N37: Asymptotic results on arithmetic functions
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 103 , Issue 2 , October 2017 , pp. 231 - 249
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

Footnotes

This work is supported by JSPS KAKENHI: 26400030, 15K17512, and 15K04778.

References

Ayoub, R. and Chowla, S., ‘On a theorem of Müller and Carlits’, J. Number Theory 2 (1970), 342–344.Google Scholar
Furuya, J., Minamide, M. and Tanigawa, Y., ‘Representations and evaluations of the error term in a certain divisor problem’, Math. Slovaca 66 (2016), 575–582.CrossRefGoogle Scholar
Furuya, J. and Tanigawa, Y., ‘On integrals and Dirichlet series obtained from the error term in the circle problem’, Funct. Approx. Comment. Math. 51 (2014), 303–333.CrossRefGoogle Scholar
Gonek, S. M., ‘Mean values of the Riemann zeta-function and its derivatives’, Invent. Math. 75 (1984), 123–141.Google Scholar
Ivić, A., The Riemann Zeta-Function (Dover, Mineola, 2003).Google Scholar
Jutila, M., Lectures on a Method in the Theory of Exponential Sums (Springer, Bombay, 1987).Google Scholar
Krätzel, E., Lattice Points (Kluwer Academic, Dordrecht, 1988).Google Scholar
Minamide, M., ‘The truncated Voronoï formula for the derivative of the Riemann zeta function’, Indian J. Math. 55 (2013), 325–352.Google Scholar
Titchmarsh, E. C., The Theory of the Riemann Zeta-Function, 2nd edn (ed. Heath-Brown, D. R.) (Oxford University Press, Oxford, 1986).Google Scholar