No CrossRef data available.
Article contents
MAXIMAL SEMIGROUP SYMMETRY AND DISCRETE RIESZ TRANSFORMS
Published online by Cambridge University Press: 14 December 2015
Abstract
We raise a question of whether the Riesz transform on 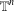 $\mathbb{T}^{n}$ or
$\mathbb{T}^{n}$ or 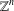 $\mathbb{Z}^{n}$ is characterized by the ‘maximal semigroup symmetry’ that the transform satisfies. We prove that this is the case if and only if the dimension is one, two or a multiple of four. This generalizes a theorem of Edwards and Gaudry for the Hilbert transform on
$\mathbb{Z}^{n}$ is characterized by the ‘maximal semigroup symmetry’ that the transform satisfies. We prove that this is the case if and only if the dimension is one, two or a multiple of four. This generalizes a theorem of Edwards and Gaudry for the Hilbert transform on 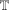 $\mathbb{T}$ and
$\mathbb{T}$ and 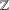 $\mathbb{Z}$ in the one-dimensional case, and extends a theorem of Stein for the Riesz transform on
$\mathbb{Z}$ in the one-dimensional case, and extends a theorem of Stein for the Riesz transform on 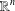 $\mathbb{R}^{n}$. Unlike the
$\mathbb{R}^{n}$. Unlike the  $\mathbb{R}^{n}$ case, we show that there exist infinitely many linearly independent multiplier operators that enjoy the same maximal semigroup symmetry as the Riesz transforms on
$\mathbb{R}^{n}$ case, we show that there exist infinitely many linearly independent multiplier operators that enjoy the same maximal semigroup symmetry as the Riesz transforms on 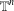 $\mathbb{T}^{n}$ and
$\mathbb{T}^{n}$ and 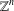 $\mathbb{Z}^{n}$ if the dimension
$\mathbb{Z}^{n}$ if the dimension  $n$ is greater than or equal to three and is not a multiple of four.
$n$ is greater than or equal to three and is not a multiple of four.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2015 Australian Mathematical Publishing Association Inc.


