Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-17T23:15:00.847Z Has data issue: false hasContentIssue false
  • English
  • Français

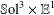$\mathbb{S}\text{ol}^{3}\times \mathbb{E}^{1}$-MANIFOLDS

Part of: Global differential geometry Low-dimensional topology

Published online by Cambridge University Press:  04 December 2017

J. A. HILLMAN
J. A. HILLMAN*
Affiliation:
School of Mathematics and Statistics, University of Sydney, Sydney, NSW 2006, Australia email jonathan.hillman@sydney.edu.au
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that closed 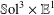$\mathbb{S}\text{ol}^{3}\times \mathbb{E}^{1}$-manifolds are Seifert fibred, with general fibre the torus, and base one of the flat 2-orbifolds 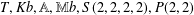$T,Kb,\mathbb{A},\mathbb{M}b,S(2,2,2,2),P(2,2)$ or 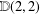$\mathbb{D}(2,2)$, and outline how such manifolds may be classified.

Keywords

lattice4-manifoldSeifert fibrationsolvable Lie groupSol3 ×E1

MSC classification

Primary: 57M50: Geometric structures on low-dimensional manifolds
Secondary: 53C30: Homogeneous manifolds
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 105 , Issue 1 , August 2018 , pp. 46 - 56
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Cobb, R., ‘Infrasolvmanifolds of dimension four’, PhD Thesis, School of Mathematics and Statistics, University of Sydney, 1999.Google Scholar
Dekimpe, K., Almost Bieberbach Groups: Affine and Polynomial Structures, Lecture Notes in Mathematics, 1639 (Springer, Berlin, 1996).Google Scholar
Hillman, J. A., Four-Manifolds, Geometries and Knots, GT Monographs, 5 (Geometry and Topology Publications, Coventry, 2002), revised in 2007 and 2014.Google Scholar
Hillman, J. A., ‘Geometries and infrasolvmanifolds in dimension 4’, Geom. Dedicata (2007), 57–72.Google Scholar
Hillman, J. A., ‘The F2 -cohomology rings of Sol3 -manifolds’, Bull. Aust. Math. Soc. 89 (2014), 191–201.Google Scholar
Lee, K. B. and Thuong, S., ‘Infra-solvmanifolds of Sol1 4 ’, J. Korean Math. Soc. 52 (2015), 1209–1251.Google Scholar
Montesinos, J. M., Classical Tessellations and Three-Manifolds, Universitext (Springer, Berlin, 1987).Google Scholar
Raghunathan, M., Discrete Subgroups of Lie Groups, Ergebnisse der Mathematik und ihrer Grenzgebiete, Folge 2, Bd 68 (Springer, Berlin, 1972).CrossRefGoogle Scholar
Sakamoto, K. and Fukuhara, S., ‘Classification of T 2 -bundles over T 2 ’, Tokyo J. Math. 6 (1983), 311–327.Google Scholar
Wall, C. T. C., ‘Geometric structures on compact complex analytic surfaces’, Topology 25 (1986), 119–153.Google Scholar