Article contents
LITTLEWOOD–PALEY CHARACTERIZATION OF WEIGHTED HARDY SPACES ASSOCIATED WITH OPERATORS
Published online by Cambridge University Press: 10 November 2016
Abstract
Let 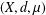 $(X,d,\unicode[STIX]{x1D707})$ be a metric measure space endowed with a distance
$(X,d,\unicode[STIX]{x1D707})$ be a metric measure space endowed with a distance 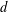 $d$ and a nonnegative, Borel, doubling measure
$d$ and a nonnegative, Borel, doubling measure 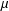 $\unicode[STIX]{x1D707}$. Let
$\unicode[STIX]{x1D707}$. Let 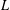 $L$ be a nonnegative self-adjoint operator on
$L$ be a nonnegative self-adjoint operator on 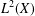 $L^{2}(X)$. Assume that the (heat) kernel associated to the semigroup
$L^{2}(X)$. Assume that the (heat) kernel associated to the semigroup 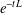 $e^{-tL}$ satisfies a Gaussian upper bound. In this paper, we prove that for any
$e^{-tL}$ satisfies a Gaussian upper bound. In this paper, we prove that for any 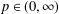 $p\in (0,\infty )$ and
$p\in (0,\infty )$ and 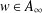 $w\in A_{\infty }$, the weighted Hardy space
$w\in A_{\infty }$, the weighted Hardy space 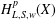 $H_{L,S,w}^{p}(X)$ associated with
$H_{L,S,w}^{p}(X)$ associated with 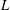 $L$ in terms of the Lusin (area) function and the weighted Hardy space
$L$ in terms of the Lusin (area) function and the weighted Hardy space 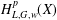 $H_{L,G,w}^{p}(X)$ associated with
$H_{L,G,w}^{p}(X)$ associated with 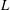 $L$ in terms of the Littlewood–Paley function coincide and their norms are equivalent. This improves a recent result of Duong et al. [‘A Littlewood–Paley type decomposition and weighted Hardy spaces associated with operators’, J. Geom. Anal.26 (2016), 1617–1646], who proved that
$L$ in terms of the Littlewood–Paley function coincide and their norms are equivalent. This improves a recent result of Duong et al. [‘A Littlewood–Paley type decomposition and weighted Hardy spaces associated with operators’, J. Geom. Anal.26 (2016), 1617–1646], who proved that 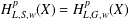 $H_{L,S,w}^{p}(X)=H_{L,G,w}^{p}(X)$ for
$H_{L,S,w}^{p}(X)=H_{L,G,w}^{p}(X)$ for 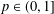 $p\in (0,1]$ and
$p\in (0,1]$ and 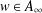 $w\in A_{\infty }$ by imposing an extra assumption of a Moser-type boundedness condition on
$w\in A_{\infty }$ by imposing an extra assumption of a Moser-type boundedness condition on 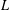 $L$. Our result is new even in the unweighted setting, that is, when
$L$. Our result is new even in the unweighted setting, that is, when 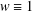 $w\equiv 1$.
$w\equiv 1$.
Keywords
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 103 , Issue 2 , October 2017 , pp. 250 - 267
- Copyright
- © 2016 Australian Mathematical Publishing Association Inc.
References
- 6
- Cited by


