Article contents
Ideals of compact operators
Published online by Cambridge University Press: 09 April 2009
Abstract
We give an example of a Banach space X such that K (X, X) is not an ideal in K (X, X**). We prove that if z* is a weak* denting point in the unit ball of Z* and if X is a closed subspace of a Banach space Y, then the set of norm-preserving extensions H B(x* ⊗ z*) ⊆ 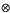 (Z*, Y)* of a functional x* ⊗ Z* ∈ (Z ⊗ X)* is equal to the set H B(x*) ⊗ {z*}. Using this result, we show that if X is an M-ideal in Y and Z is a reflexive Banach space, then K (Z, X) is an M-ideal in K(Z, Y) whenever K (Z, X) is an ideal in K (Z, Y). We also show that K (Z, X) is an ideal (respectively, an M-ideal) in K (Z, Y) for all Banach spaces Z whenever X is an ideal (respectively, an M-ideal) in Y and X * has the compact approximation property with conjugate operators.
(Z*, Y)* of a functional x* ⊗ Z* ∈ (Z ⊗ X)* is equal to the set H B(x*) ⊗ {z*}. Using this result, we show that if X is an M-ideal in Y and Z is a reflexive Banach space, then K (Z, X) is an M-ideal in K(Z, Y) whenever K (Z, X) is an ideal in K (Z, Y). We also show that K (Z, X) is an ideal (respectively, an M-ideal) in K (Z, Y) for all Banach spaces Z whenever X is an ideal (respectively, an M-ideal) in Y and X * has the compact approximation property with conjugate operators.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 2004
References
- 10
- Cited by


