Article contents
FACTORISATION OF EQUIVARIANT SPECTRAL TRIPLES IN UNBOUNDED 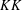 $KK$-THEORY
$KK$-THEORY
Published online by Cambridge University Press: 21 December 2018
Abstract
We provide sufficient conditions to factorise an equivariant spectral triple as a Kasparov product of unbounded classes constructed from the group action on the algebra and from the fixed point spectral triple. We show that if factorisation occurs, then the equivariant index of the spectral triple vanishes. Our results are for the action of compact abelian Lie groups, and we demonstrate them with examples from manifolds and 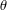 $\unicode[STIX]{x1D703}$-deformations. In particular, we show that equivariant Dirac-type spectral triples on the total space of a torus principal bundle always factorise. Combining this with our index result yields a special case of the Atiyah–Hirzebruch theorem. We also present an example that shows what goes wrong in the absence of our sufficient conditions (and how we get around it for this example).
$\unicode[STIX]{x1D703}$-deformations. In particular, we show that equivariant Dirac-type spectral triples on the total space of a torus principal bundle always factorise. Combining this with our index result yields a special case of the Atiyah–Hirzebruch theorem. We also present an example that shows what goes wrong in the absence of our sufficient conditions (and how we get around it for this example).
MSC classification
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 107 , Issue 2 , October 2019 , pp. 145 - 180
- Copyright
- © 2018 Australian Mathematical Publishing Association Inc.
References
- 3
- Cited by




